-
光传输网(OTN)是由光纤链路组成的光网络,其信号传输速率可达100 Gbits/s或更高。为推动100G光通信的发展,ITU-T于2009年更新了OTN接口建议G.709,并定义了OTU4帧结构和映射协议,其纠错码方案不仅具有极低的误码率(bit error rate, BER),也不存在错误平层的问题[1]。随着网络与通信技术的飞速发展,人们开始追求更高的OTN信号传输速率和更低的误码率。为此,针对下一代OTN通信,如何设计一种高速纠错码方案,满足OTN通信的严格要求,如低实现复杂度,逼近香农限性能,无错误平层等,成为了研究的重点。
低密度校验(low density parity check, LDPC)码是最具前景的近香农限纠错码方案之一,已被确定为5G移动宽带业务数据信息的长码编码方案[2]。然而,当LDPC码应用于OTN环境中,编码复杂度是不能忽略的问题。一般来说,LDPC码通常需要二次方的编码复杂度,所以在实现过程中需要对校验矩阵进一步优化。作为LDPC码的特例,低密度生成矩阵(LDGM)码不仅具有更低的线性编码复杂度,同时也可以用置信传播(BP)算法实现低复杂度解码[3]。但LDGM码的校验矩阵存在大量度为1的列,这导致了较高的错误平层[4]。
文献[5]基于信道极化现象提出了一种名为Polar码的纠错码方案,并利用连续取消(successive cancellation, SC)解码算法证明了所构造的Polar码可以达到对称二元离散无记忆信道(binary-input discrete memoryless channels, BDMC)的信道容量。与LDPC码相比,Polar码同时具有低编解码复杂度,无错误平层等优势[6-7],目前已被确定为5G增强移动宽带场景的控制信道编码方案[8]。但是,相比于渐进理论性能,如仍采用SC解码算法,则有限码长的Polar码在OTN应用无法保证BER要求[9-10]。因此大量的研究工作着眼于改进Polar码的解码算法,提高其解码性能[11-13]。
文献[6]首次针对OTN提出了一种Polar-LDPC级联码方案,获得比OTN中已有纠错码方案更好的性能。文献[14]则针对无线通信系统提出了一种Polar-LDGM码方案,相比于Polar码和LDGM码分别获得了一定的性能增益。然而,Polar-LDPC码和文献[14]中的Polar-LDGM码构造方法是通过仿真实验得到的,并没有经过理论验证。此外,Polar码所观测的信道被假设成是一个虚拟的二元删除信道(binary erasure channel, BEC),Polar码是基于此信道并利用文献[5]中的启发式构造方法来实现编码,其码率为该BEC信道的容量,因此,Polar码的设计不是最优的。另外,与文献[14]适用的无线通信系统不同,OTN网络对编码码率、误码率和错误平层的要求都更高。文献[15-17]则从编解码方法的角度研究了与Polar码相关的其他级联码方案,但是并没有具体讨论实际通信系统适用性问题。
基于此,本文从实际应用背景出发,提出了一种将Polar码作为外码,LDGM码作为内码的高速级联Polar-LDGM码编解码方案,并研究其在OTN中的编码复杂度、BER性能和错误平层存在性的问题。为使得高速Polar-LDGM码构造理论更加完备,考虑到Polar码和LDGM码均可以用BP算法解码,故本文基于高斯逼近法(GA)的思想,通过仅需追踪消息的均值,即可从理论上实现对Polar-LDGM码的有效构造,从而完成BER性能的分析。仿真结果表明,本文所提出的方案在BER性能上优于Polar-LDPC码级联方案,获得了逼近容量的性能,直到BER为10-10也没有出现错误平层,并且Polar-LDGM码具有更低的编码复杂度。
-
本节主要分析Polar码和LDGM码的基本构造原理,并对它们的编解码方法和错误平层问题进行讨论,该研究对本文所提出的级联码方案起着至关重要的作用。
-
基于信道极化现象可以实现Polar码的构造,信道极化主要包括信道合成和信道分离两种操作[18]。首先令$W:\mathcal{X} \to \mathcal{Y}$表示一个BDMC信道,其中$\mathcal{X} = \{ 0,1\} $为二元输入符号集,$\mathcal{Y}$为任意输出符号集,并且当$x \in \mathcal{X}$和$y \in \mathcal{Y}$时,转移概率为$W(y|x)$。定义$W^{N}(\boldsymbol{y} | \boldsymbol{x})$为N个独立的信道W,满足$W^{N}(\boldsymbol{y} | \boldsymbol{x})= \prod\nolimits_{i = 1}^N {W({y_i}|{x_i})} $,其中,${\boldsymbol{x}} = [{x_1},{x_2}, \cdots ,$ ${x_N}]$,${\boldsymbol{y}} = [{y_1},{y_2}, \cdots ,{y_N}]$。考虑一个长度为N且由0和1组成的行向量u,并令$\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{u}}{\mathit{\boldsymbol{G}}_N}$为N个信道W的输入,则可定义${W_N}(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{x}})$为合成信道,并满足:${W_N}(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{u}}) = {W_N}(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{u}}{\mathit{\boldsymbol{G}}_N})$,其中,${\mathit{\boldsymbol{G}}_N}$是生成矩阵[5]。然后,令$W_N^{(i)}:\mathcal{X} \to {\mathcal{Y}^N} \times {\mathcal{X}^{i - 1}}$为N个极化比特信道,由合成信道${W_N}(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{x}})$按式(1)分离而来:
$$W_N^{(i)}(\mathit{\boldsymbol{y}},\mathit{\boldsymbol{u}}_1^{i - 1}|{u_i}) = \sum\limits_{\mathit{\boldsymbol{u}}_{i + 1}^N} {\frac{1}{{{2^{N - 1}}}}} {W_N}(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{x}})$$ (1) 式中,$i \in [N] \triangleq \{ 1,2, \cdots ,N\} $,且对于$i < j$,$\mathit{\boldsymbol{u}}_i^j \subseteq \mathit{\boldsymbol{u}}$表示子向量$[{u_i},{u_{i + 1}}, \cdots ,{u_j}]$。文献[5]表明,当$N \to \infty $时,比特信道$W_N^{(i)}$不断极化,相应的Bhattacharyya参数$Z(W_N^{(i)})$会越来越趋近于0或1,而那些无噪的极化比特信道(即$Z(W_N^{(i)}) = 0$)的容量接近于对称信道容量I(W)。
Polar码编码的核心是通过$Z(W_N^{(i)})$逼近0的那些极化比特信道$W_N^{(i)}$发送信息比特,同时通过$Z(W_N^{(i)})$逼近1的那些极化比特信道$W_N^{(i)}$发送收发端均已知的固定比特。因此,考虑集合[N],定义$\mathcal{A} \subseteq [N]$为信息比特索引集合,并令固定比特索引集合为$\mathcal{F} = [N]\backslash \mathcal{A}$,表示那些在[N]中且不在$\mathcal{A}$中的比特索引集合。相应地,向量u可以被分为两个独立的子向量$\mathit{\boldsymbol{u}} = ({\mathit{\boldsymbol{u}}_\mathcal{A}},{\mathit{\boldsymbol{u}}_\mathcal{F}})$,其中,${\mathit{\boldsymbol{u}}_\mathcal{A}}$表示子向量$[u:i \in \mathcal{A}]$,故Polar码可编码为:
$$\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{u}}_\mathcal{A}}{\mathit{\boldsymbol{G}}_\mathcal{A}} + {\mathit{\boldsymbol{u}}_\mathcal{F}}{\mathit{\boldsymbol{G}}_\mathcal{F}}$$ (2) 式中,${\mathit{\boldsymbol{G}}_\mathcal{A}}$和${\mathit{\boldsymbol{G}}_\mathcal{F}}$分别是Polar码生成矩阵${\mathit{\boldsymbol{G}}_N}$的子矩阵,且分别由$\mathcal{A}$和$\mathcal{F}$中的索引所对应的行构成。经过推导证明,上述Polar码的编码复杂度仅为$O(N\log N)$,其中,N是码长,$O( \cdot )$是Landau符号[5]。
对于Polar码的解码,Arikan利用所设计的SC解码算法证明了Polar码的信道容量可达性。当Polar码的码率满足:
$$\mathop {\lim }\limits_{N \to \infty } R = \mathop {\lim }\limits_{N \to \infty } \frac{{\left| \mathcal{A} \right|}}{N} \leqslant I(W)$$ (3) 对于任意的$\beta \in(0,1 / 2)$,分组错误概率${P_e}$为:
$${P_e} \leqslant \sum\limits_{i \in A} {Z(W_N^{(i)})} = {2^{ - {N^\beta }}}$$ (4) 相比于SC解码算法,Polar码的BP解码算法具有与SC解码算法一样的错误概率界,不仅只有$O(N)$的解码复杂度,还可以改善有限长度Polar码的BER性能[9],故更适用于以下提出的级联码解码方案。
由于Polar码的BP解码也是通过Tanner图实现的,所以有必要分析其停止距离和最小停止集,而这两点对Polar码解码失败原因和错误平层的分析非常重要[19]。此外,围长也是用于分析错误平层的另一个重要的因素。基于文献[6-7]的结论,总结如下定理。
定理1 长度为N的Polar码的停止距离为$O\left( {\sqrt N } \right)$,码长为8或更长的Polar码所对应Tanner图的围长至少为12。
该定理表明,正是具有如此大的停止距离与围长,Polar码很难出现错误平层。
-
LDGM码也是一种线性分组码,它的稀疏校验矩阵可以表示为$\mathit{\boldsymbol{H}} = [{\mathit{\boldsymbol{P}}^{\rm{T}}}|\mathit{\boldsymbol{I}}]$,其中左侧的P是随机矩阵,${( \cdot )^{\rm{T}}}$是转置符号,右侧的I是$K \times K$单位矩阵[3]。如果K表示信息比特数,N是码长,则LDGM码的码率为K/N。
当待传信息比特和校验比特分别表示为$\mathit{\boldsymbol{u}} = [{u_1},{u_2}, \cdots ,{u_K}]$和$\mathit{\boldsymbol{p}} = [{p_1},{p_1}, \cdots ,{p_{N - K}}]$时,则LDGM码的码字序列为$\mathit{\boldsymbol{c}} = [{u_1},{u_2}, \cdots ,{u_K},{p_1},{p_2}, \cdots ,$ ${p_{N - K}}]$,且必须满足校验关系$\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{c}}^{\rm{T}}} = {\bf{0}}$。由于c中的校验比特完全由矩阵H确定,故无需将H转换成对应的生成矩阵,即满足:
$$\begin{array}{*{20}{c}} {{p_m} = \sum\limits_{k = 1}^K {{u_k}{h_{m,k}}} }&{1 \leqslant m \leqslant N - K} \end{array}$$ (5) 式中,${h_{m,k}}$表示H中第m行、第k列元素。因此,LDGM码的编码速度较快,编码复杂度较低。此外,与LDPC码类似,LDGM码也可以使用BP算法解码。
LDGM码与LDPC码唯一的不同之处是LDGM码的Tanner图中存在N-K个度为1的校验比特节点。所以在解码过程中,无法更新相应校验节点的消息,这就导致了高错误平层。另外,文献[20]表明当LDGM码的码率低于0.9的时候,错误平层较高、BER性能较差。但当码率超过0.9时,LDGM码的BER性能会得到极大改善。原因是码率越大,矩阵I的维度就越小,对应的度为1的节点数越少。因此,LDGM码非常适用于高码率应用的场所。
-
本节首先针对级联信道模型具体阐述Polar- LDGM码的编码设计方案和相应的解码算法。然后,基于GA法对所提出的方案进行BER分析。
-
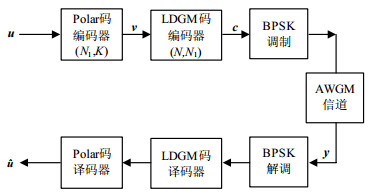
本文所提出的Polar-LDGM码方案如图 1所示。具体来说,首先用$({N_1},K)$Polar码对二元信息比特$\mathit{\boldsymbol{u}} = [{u_1},{u_2}, \cdots ,{u_K}]$编码,得到码字$\mathit{\boldsymbol{v}} = [{v_1},{v_2}, \cdots ,{v_N}]$。然后,用$(N,{N_1})$LDGM码对v再次编码,输出码字$\mathit{\boldsymbol{c}} = [{v_1},{v_2}, \cdots ,{v_{{N_1}}},{p_1},{p_2}, \cdots ,{p_{N - {N_1}}}]$,其中,$\mathit{\boldsymbol{p}} = $ $[{p_1},{p_2}, \cdots ,{p_{N - {N_1}}}]$是LDGM码的校验比特,故整个级联码的码率是$K/N$。在经过二进制相移键控(binary-phase shift- keying, BPSK)调制之后,信号通过方差为${\sigma ^2} = {N_0}/2$的加性高斯白噪声(additive Gaussian noise, AWGN)信道。在接收到信号$\mathit{\boldsymbol{y}} = [{y_1},{y_2}, \cdots ,{y_N}]$后,LDGM解码器首先利用其校验矩阵解码,然后Polar码解码器再利用LDGM解码器输出的对数似然比(log likelihood ratio, LLR)作为先验信息对Polar码解码器进行初始化。Polar码解码完成后,即可得到u的估计值$ \boldsymbol{\hat u}$。
对于文献[6]中的Polar-LDPC来说,LDPC码编码复杂度的问题是必须考虑的问题,因为编码器需要存储一个校验矩阵和对应的占存储空间为$O({N^2})$的生成矩阵。一般来说,LDPC码的编码过程需要花费二次方的时间。另一方面,对于Polar-LDGM码来说,其LDGM编码器仅需要存储一个大小为$O(N)$的校验矩阵,而Polar码编码器仅需要存储一个大小为$O({N_1}\log {N_1})$的生成矩阵。总之,Polar-LDGM码编码器的硬件资源消耗比Polar- LDPC码低,具体如表 1所示。
表 1 Polar-LDGM码与Polar-LDPC码编码复杂度比较
Polar-LDPC Polar-LDGM 存储
空间矩阵H:$O(N)$ 矩阵H:$O(N)$ 矩阵G:
$O({N_1}\log {N_1}),$$O({N^2})$矩阵G:
$O({N_1}\log {N_1})$编码
时间$O({N_1}\log {N_1}) + O({N^2})$ $O({N_1}\log {N_1}) + O(N)$ -
在收到y后,LDGM解码器和Polar码解码器分别依次执行BP解码,级联解码算法的具体步骤如算法1所示。
算法1 Polar-LDGM码解码算法
1) 输入接收信号y
2) 接收信号y的LLR值:
$$L({c_i}) = \log \frac{{p\left( {{y_i}|{c_i} = 0} \right)}}{{p({y_i}|{c_i} = 1)}} = \frac{{2{y_i}}}{{{\sigma ^2}}}$$ 3) 第一次初始化:
//令$L({q_{ij}})$和$L({r_{ji}})$分别为变量
节点${v_i}$和校验节点${s_j}$的初始化信息
4) $ {L({q_{ij}}) = L({v_i}){\rm{ = }}L({c_i})}\;\;{1 \leqslant i \leqslant {N_1}} $
5) $ L({r_{ji}}) = L({s_j}) = L({c_i})\;\;\;{N_1} + 1 \le i \le N$
6) LDGM迭代解码
7) 当$t \leqslant {t_{{\rm{ldgm}}}}$执行
//tldgm是LDGM码解码器的最大迭代次数
8) 更新
$L({r_{ji}}) = 2{\tanh ^{ - 1}}(L({s_j})\prod\limits_{i' \in {V_j},i' \ne i} {\tanh (L({q_{i'j}}/2)))} $
//从${s_j}$到${v_i}$的消息传递更新值
//其中,$ \tanh (x/2) = ({e^x} - 1)/({e^x} + 1)$,
//${V_j}$表示${v_i}$连接${s_j}$的集合
9) 更新$L({q_{ij}}) = L({v_i}) + \sum\limits_{j' \in {S_i},j' \ne j} {L({r_{j'i}})} $
//从${v_i}$到${s_j}$的消息传递更新值
//其中,${S_i}$为${s_j}$连接${v_i}$的集合
10) 更新第i个系统比特节点的全部LLR信息$L({Q_i}) = L({v_i}) + \sum\limits_{j \in {S_i}} {L({r_{ji}})} $
11) 第二次初始化://LDGM解码器的输出软信息可以作为Polar码解码器的输入
12) ${L_{{n_1} + 1,i}} = L({Q_i})$//表示Tanner图中从右至左传递的初始化信息,$1 \leqslant l \leqslant {n_1} + 1$,$1 \leqslant i \leqslant {N_1}$
13) 如果$\:l \in \mathcal{A}$,则${R_{1,i}} = 0$
//表示Tanner图中从左至右传递的初始化信息
否则 如果 $l \in \mathcal{F}$,则${R_{1,i}} = \infty $
14) Polar码迭代解码:
15) 当$t \leqslant {t_{{\rm{polar}}}}$执行
//tpolar是Polar码解码器的最大迭代次数
16) 更新
$ {L_{l,i}} = f({L_{l + 1,i}},{L_{l + 1,i + {N_l}}} + {R_{l,i + {N_l}}})$
$ {L_{l,i + {N_l}}} = {L_{l + 1,i + {N_l}}} + f({L_{l + 1,i}},{R_{l,i}})$
$ {R_{l + 1,i}} = f({R_{l,i}},{L_{l + 1,i + {N_l}}} + {R_{l + 1,i + {N_l}}})$
${R_{l + 1,i + {N_l}}} = {R_{l,i + {N_l}}} + f({R_{l,i}},{L_{l + 1,i}})$//${N_l} = {2^{{n_1} - l}}$
17) 最终决策:
18) 如果${L_{1,i}} + {R_{1,i}} < 0$,则${\hat u_i} = 1$
//表示信息比特的估计值
否则,${\hat u_i} = 0 $
19) 迭代停止准则:
20) 如果$\mathit{\boldsymbol{\hat x}} = \mathit{\boldsymbol{\hat u}}{G_N}$,则$\mathit{\boldsymbol{\hat u}}$就是u的有效估计值,
故停止后续的迭代
否则,返回步骤14)执行下一次迭代,直到迭代次数达到${t_{{\rm{polar}}}}$为止。
21) 输出:$\mathit{\boldsymbol{\hat u}} $
在算法1的步骤16)中,对于任意两个实数x和y,有$f(x,y) = \ln ((1 + xy)/(x + y))$。而为了快速执行,函数$f(x,y)$的计算可以近似为$f(x,y) \approx {\rm{sign}}(x){\rm{sign}}(y)\min(|x|,|y|)$,而不会带来太大的性能损失[13]。
从对第二节的分析可知,将Polar码与LDGM码级联,预期会得到较好的BER性能,原因主要有以下3点:
1) 当LDGM码的码率高于0.9时,LDGM码具有极好的收敛性能。虽然在低至${\rm{BER}} = {10^{ - 7}}$~${10^{ - 8}}$时,LDGM码仍然会出现错误平层,但是当BER曲线出现陡降时,SNR极低,即曲线逼近香农容量限[20]。
2) 当LDGM码解码出错时,几乎每个分组都存在错误,但每个分组中的错误数都极低,而级联一个高码率的外码就可以移除大部分的错误[3]。所以这种特性就确保了Polar-LDGM码具有非常好的陡降特性。
3) 从定理1可知,由于具有较大的停止距离和围长,Polar码作为外码不仅可以消除LDGM码解码所带来的错误平层,同时也可以进一步移除LDGM码解码的剩余错误。另外,为了使得Polar码码率的损失最小,应设置LDGM码码率尽量接近于级联码码率,相应地,Polar码码率接近于1。
因此,Polar码和LDGM码的级联设计,不仅吸取了两种码各自的优点,还克服了各自的缺点。所提出的Polar-LDGM码预期会达到逼近香农信道容量限,并且具有较低的编解码复杂度,也不存在错误平层问题。
-
因为算法1计算出的$L({c_i})$均是高斯随机变量,故LDGM码解码器在第t次迭代的第i个变量节点的输出均值为:
$$\mu _{v,i}^t = {\mu _{0,i}} + ({d_v} - 1)\mu _{c,j}^{t - 1}$$ (6) 式中,${\mu _{0,i}}$是观测y所得到的第i个信道消息的初始均值,$\mu _{c,j}^{t - 1}$是在第t-1次迭代时,来自第j个校验节点的输入消息的均值,${d_v}$是变量节点的度。均值$\mu _{c,j}^{t - 1}$计算如下:
$$\mu _{c,j}^t = {\phi ^{ - 1}}(1 - {(1 - \phi ({\mu _{0,i}} + ({d_v} - 1)\mu _{c,j}^{t - 1}))^{{d_c} - 1}})$$ (7) 式中,${d_c}$是校验节点的度;且对于$\mu \geqslant 0$,函数$\phi (\mu )$定义为:
$$\phi (\mu ) \triangleq 1 - \frac{1}{{\sqrt {4\pi \mu } }}\int_{ - \infty }^\infty {\tanh \left( {\frac{\tau }{2}} \right)} \exp \left[ { - \frac{{{{(\tau - \mu )}^2}}}{{4\mu }}} \right]{\rm{d}}\tau $$ (8) 在实际应用中,$\phi (\mu )$可近似为:
$$\phi (\mu ) \simeq \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\exp ( - 0.4527{\mu ^{0.86}}{\rm{ + }}0.0218)}&{\begin{array}{*{20}{c}} {}&{0 < \mu < 10} \end{array}} \end{array}} \\ {\begin{array}{*{20}{c}} {\sqrt {\frac{\pi }{\mu }} \exp \left( {\frac{{ - \mu }}{4}} \right)\left( {1 - \frac{{10}}{\mu }} \right)}&{}&{\mu > 10} \end{array}} \end{array}} \right.$$ (9) LDGM解码器迭代完成后,获得的最终均值$\mu _{v,i}^{{t_{{\rm{ldgm}}}}}$被传递至所级联的Polar码解码器中实现初始化操作。接着,可以继续更新Polar码每个变量节点的LLR值:
$$L_{l,i}^t = 2{\tanh ^{ - 1}}\left( {\tanh \left( {\frac{{L_{l + 1,i}^{t - 1}}}{2}} \right)\tanh \left( {\frac{{L_{l + 1,i + {N_l}}^{t - 1} + R_{l,i + {N_l}}^{t - 1}}}{2}} \right)} \right)$$ $$L_{l,i + {N_l}}^t = L_{l + 1,i + {N_l}}^{t - 1} + 2{\tanh ^{ - 1}}\left( {\tanh \left( {\frac{{L_{l + 1,i}^{t - 1}}}{2}} \right)\tanh \left( {\frac{{R_{l,i}^{t - 1}}}{2}} \right)} \right)$$ $$R_{l + 1,i}^t = 2{\tanh ^{ - 1}}\left( {\tanh \left( {\frac{{R_{l,i}^{t - 1}}}{2}} \right)\tanh \left( {\frac{{L_{l + 1,i + {N_l}}^{t - 1} + R_{l + 1,i + {N_l}}^{t - 1}}}{2}} \right)} \right)$$ $$R_{l + 1,i + {N_l}}^t = R_{l,i + {N_l}}^{t - 1} + 2\tanh{^{ - 1}}\left( {\tanh \left( {\frac{{L_{l + 1,i}^{t - 1}}}{2}} \right)\tanh \left( {\frac{{R_{l,i}^{t - 1}}}{2}} \right)} \right)$$ (10) 式中,$L_{l,i}^t$和$R_{l,i}^t$分别是第t次迭代变量节点的左右LLR值。
由于式(10)计算出的值也是高斯随机变量,故满足关系${\rm{D}}[L_{l,i}^t] = 2{\rm{E}}[L_{l,i}^t]$和${\rm{D}}[R_{l,i}^t] = 2{\rm{E}}[R_{l,i}^t]$,其中,${\rm{D}}[ \cdot ]$和${\rm{E}}[ \cdot ]$分别是方差和均值。因此,只需通过跟踪均值${\rm{E}}[L_{l,i}^t]$和${\rm{E}}[R_{l,i}^t]$即可实现BER性能的分析。将均值${\rm{E}}[L_{l,i}^t]$和${\rm{E}}[R_{l,i}^t]$分别简写成$\mu _{l,i}^{{\rm{left}},{\rm{t}}}$和$\mu _{l,i}^{{\rm{right}},{\rm{t}}}$,则均值计算如下:
$$\mu _{l,i}^{{\rm{left}},{\rm{t}}} = {\phi ^{ - 1}}\left( {1 - {{\left[ {1 - \phi \left( {\mu _{l + 1,(i + 1)/2}^{{\rm{left}},{\rm{t}}}} \right)} \right]}^2}} \right)$$ $$\mu _{l,i + {N_l}}^{{\rm{left}},{\rm{t}}}{\rm{ = 2}}\mu _{l + 1,(i + {N_l})/2}^{{\rm{left}},{\rm{t}}}$$ $$\mu _{l + 1,i}^{{\rm{right}},{\rm{t}}} = {\phi ^{ - 1}}\left( {1 - {{\left[ {1 - \phi \left( {\mu _{l + 2,(i + 1)/2}^{{\rm{right}},{\rm{t}}}} \right)} \right]}^2}} \right)$$ $$\mu _{l + 1,i + {N_l}}^{{\rm{right}},{\rm{t}}}{\rm{ = 2}}\mu _{l + 2,(i + {N_l})/2}^{{\rm{right}},{\rm{t}}}$$ (11) 式中,函数$\phi ( \cdot )$的计算方法同式(8)和式(9)。在递归计算的最后,令:
$$\mu _{{n_1} + 1,i}^{{\rm{left}},0} = \mu _{v,i}^{{t_{{\rm{ldgm}}}}}$$ (12) 所以,第i个极化比特信道的错误概率为:
$$P_e^{(i)} = \frac{1}{2}{\rm{erfc}}\left( {\frac{{\sqrt {\mu _{1,i}^{{\rm{left}},{t_{{\rm{polar}}}}} + \mu _{1,i}^{{\rm{right}},{t_{{\rm{polar}}}}}} }}{2}} \right)$$ (13) 式中,
$$\operatorname{erfc}(x)=(2 / \sqrt{\pi}) \int_{x}^{\infty} \mathrm{e}^{-\eta^{2}} \mathrm{d} \eta$$ 故对于所提出的Polar-LDGM编码方案,平均错误概率为:
$$\overline {{P_e}} = \frac{{\sum\limits_{i \in A} {P_e^{(i)}} }}{{\left| \mathcal{A} \right|}}$$ (14) 式中,$\mathcal{A}$为Polar码的信息比特索引集合。
-
本节通过计算机仿真对Polar-LDGM码的BER性能进行分析。假设Polar-LDGM码由$({N_1},K)$Polar码和$(N,{N_1})$LDGM码级联而成。为便于分析,本文仅考虑规则LDGM码,即矩阵P的行重和列重均一样,且是基于渐进边增长(progressive edge-growth algorithm, PEG)算法而生成[21]。具体仿真参数设置如表 2所示。
表 2 仿真参数
参数 说明 信道模型 BI-AWGN 发送功率 归一化为1 总码率R 0.93 Polar码码率RP 0.979 LDGM码码率RL 0.95 码长 N1=213, N=N1×RP/R=8 624 信息比特长度 K=N1×RP=8 020 度分布 dc=3 迭代次数 Polar码: 200
LDGM码: 100图 2比较了不同编码方案的BER性能,其中极化码码长为213,其他编码方案码长为8 624,码率均为0.93。可以看出,本文所提出的Polar-LDGM编码方案大幅度改进了Polar码的陡降性能,而且消除了LDGM码存在的错误平层问题,直到BER降到10-10时也没有发现错误平层。虽然单独使用LDPC和LDGM码的方案在低SNR时BER降的很快,但是在中高SNR时,却突然出现了错误平层。此外,由于Polar-LDGM码是经过2.3节中的GA法优化而来,故与Polar-LDPC码相比获得了更好的性能,当BER=10-7时,Polar-LDGM码比Polar-LDPC码至少改善了0.12 dB,并且Polar-LDGM码拥有更低的编码复杂度。
图 3给出了随着码长的不断增大,Polar-LDGM码的性能增益。正如预期的那样,随着${N_1}$的不断增加,BER性能得到了明显的改善,直到BER降到10-10也没有出现错误平层。本方案的信道容量限为3.73 dB(信道容量限可通过文献[22]求得),如果将BER=10-10设置为OTN可靠通信的条件,则从图中可以看出,仿真参数为${N_1} = {2^{16}}$,${R_P} = 0.989{\rm{ }}0$,${d_c} = 3$的Polar-LDGM码的性能距离信道容量限不到0.7 dB。
-
本文提出了一种基于Polar码和LDGM码的高速级联码方案,通过合理地搭建系统模型,完成了级联编码的构造,并利用BP解码算法,实现了级联解码的设计,基于GA思想,从理论上推导出Polar-LDGM码的错误概率。理论分析与仿真结果均表明,本方案不仅具有较低的编解码复杂度,还满足OTN对纠错码逼近香农限和无错误平层的要求,且优于已有的Polar-LDPC码。
下一步考虑利用外信息转移(extrinsic information transformation, EXIT)图[23]分析并构造Polar-LDGM码,以期进一步简化BER性能分析,并提高系统的性能。
Design of Polar-LDGM Codes for Optical Transport Network
-
摘要: 针对光传输网(OTN)对纠错码低实现复杂度、逼近香农限性能和无错误平层的要求,提出了一种基于Polar码和低密度生成矩阵(LDGM)码的低复杂度高速级联码方案。首先针对级联模型阐述了Polar-LDGM码的编码设计方案,并分析了编码复杂度。然后基于两种码的结构特点,给出了基于置信传播(BP)算法的级联解码算法。通过合理利用高斯逼近(GA)法推导解码算法中传递消息的均值,能够准确地预测出Polar-LDGM码的理论错误概率。仿真结果表明,Polar-LDGM码满足在OTN中应用的要求。Abstract: In order to satisfy the requirements of low complexity, capacity approaching performance and no error floor for the error correcting codes used in the optical transport network (OTN), a high-rate concatenated codes based on polar codes and low density generator matrix (LDGM) is proposed. The polar-LDGM coding scheme for the concatenated model is first described and the encoding complexity of the scheme is analyzed. And then, the concatenated decoding algorithm based on belief propagation (BP) algorithm is detailed according to the decoding structure of both codes. By reasonably using Gaussian approximation (GA) method, we derive the mean of message passed in the decoding structure, which results in the accurate prediction of the error probability for the Polar-LDGM codes. Simulation results show that the proposed scheme achieves the demands of the optical transport network (OTN).
-
表 1 Polar-LDGM码与Polar-LDPC码编码复杂度比较
Polar-LDPC Polar-LDGM 存储
空间矩阵H:$O(N)$ 矩阵H:$O(N)$ 矩阵G:
$O({N_1}\log {N_1}),$$O({N^2})$矩阵G:
$O({N_1}\log {N_1})$编码
时间$O({N_1}\log {N_1}) + O({N^2})$ $O({N_1}\log {N_1}) + O(N)$ 表 2 仿真参数
参数 说明 信道模型 BI-AWGN 发送功率 归一化为1 总码率R 0.93 Polar码码率RP 0.979 LDGM码码率RL 0.95 码长 N1=213, N=N1×RP/R=8 624 信息比特长度 K=N1×RP=8 020 度分布 dc=3 迭代次数 Polar码: 200
LDGM码: 100 -
[1] ITU-T. Recommendation G.709: Interfaces for the optical transport network (OTN).[EB/OL].[2018-03-11]. http://www.itu.int/REC/T-REC-G.709/en. [2] ORTEGA-ORTEGA A L, BRAVO-TORRES J F. Combining LDPC codes, M-QAM modulations, and IFDMA multiple-access to achieve 5G requirements[C]//2017 International Conference on Electronics, Communications and Computers (CONIELECOMP). Cholula, Mexico: IEEE, 2017: 1-5. [3] GARCIA-FRIAS J, ZHONG W. Approaching Shannon performance by iterative decoding of linear codes with low-density generator matrix[J]. IEEE Communications Letters, 2003, 7(6):266-268. doi: 10.1109/LCOMM.2003.813816 [4] MACKAY D J C. Good error-correcting codes based on very sparse matrices[J]. IEEE Transactions on Information Theory, 1999, 45(2):399-431. doi: 10.1109/18.748992 [5] ARIKAN E. Channel polarization:A method for constructing capacity achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7):3051-3073. doi: 10.1109/TIT.2009.2021379 [6] ESLAMI A, PISHRO-NIK H. On finite-length performance of polar codes:Stopping sets, error floor, and concatenated design[J]. IEEE Transactions on Communications, 2013, 61(3):919-929. doi: 10.1109/TCOMM.2013.012313.110692 [7] MONDELLI M, HASSANI S H, URBANKE R L. Unified scaling of polar codes:Error exponent, scaling exponent, moderate deviations, and error floors[J]. IEEE Transactions on Information Theory, 2016, 62(12):6698-6712. doi: 10.1109/TIT.2016.2616117 [8] DONG L, ZHAO H Y, CHEN Y, et al. Introduction on IMT-2020 5G trials in China[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(8):1849-1866. doi: 10.1109/JSAC.2017.2710678 [9] ARIKAN E. A performance comparison of polar codes and Reed-Muller codes[J]. IEEE Communications Letters, 2008, 12(6):447-449. doi: 10.1109/LCOMM.2008.080017 [10] HUSSAMI N, KORADA S B, URBANKE R L. Performance of polar codes for channel and source coding[C]//2009 IEEE International Symposium on Information Theory (ISIT). Seoul, South Korea: IEEE, 2009: 1488-1492 [11] TAL I, VARDY A. List decoding of polar codes[J]. IEEE Transactions on Information Theory, 2015, 61(5):2213-2226. doi: 10.1109/TIT.2015.2410251 [12] SARKIS G, GIARD P, VARDY A, et al. Fast list decoders for polar codes[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(2):318-328. doi: 10.1109/JSAC.2015.2504299 [13] ABBAS S M, FAN You-zhe, CHEN Ji, et al. High-throughput and energy-efficient belief propagation polar code decoder[J]. IEEE Transactions on Very Large Scale Integration Systems, 2017, 25(3):1098-1111. doi: 10.1109/TVLSI.2016.2620998 [14] 多滨, 王振永, 顾学迈.近香农容量限的低复杂度Polar-LDGM码构造方案[J].高技术通讯, 2013, 23(6):564-570. doi: 10.3772/j.issn.1002-0470.2013.06.003 DUO Bin, WANG Zhen-yong, GU Xue-mai. On construction of Shannon capacity-approaching low complexity polar-LDGM codes[J]. High Technology Letters, 2013, 23(6):564-570. doi: 10.3772/j.issn.1002-0470.2013.06.003 [15] ARIKAN E. Serially concatenated polar codes[J]. IEEE Access, 2018, 6:64549-64555. doi: 10.1109/ACCESS.2018.2877720 [16] WANG Yao-han, ZHANG Zhi-chao, ZHANG Shun-qing, et al. A unified deep learning based polar-LDPC decoder for 5G communication systems[C]//201810th International Conference on Wireless Communications and Signal Processing (WCSP). Hangzhou, China: IEEE, 2018: 1-6. [17] XU Xiao, WU Shao-hua, DONG Dan, et al. High performance short polar codes:A concatenation scheme using spinal codes as the outer code[J]. IEEE Access, 2018, 6:70644-70654. doi: 10.1109/ACCESS.2018.2879827 [18] 章新城, 李少谦. M-QAM调制下极化码的构造研究[J].电子科技大学学报, 2017, 46(2):330-334. doi: 10.3969/j.issn.1001-0548.2017.02.002 ZHANG Xin-cheng, LI Shao-qian. Research on construction of polar codes with M-QAM Modulation[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(2):330-334. doi: 10.3969/j.issn.1001-0548.2017.02.002 [19] DI C Y, PROIETTI D, TELATAR I E, et al. Finite length analysis of low-density parity-check codes on the binary erasure channel[J]. IEEE Transactions on Information Theory, 2002, 48(6):1570-1579. doi: 10.1109/TIT.2002.1003839 [20] GONZALEZ-LOPEZ M, VAZQUEZ-ARAUJO F J, CASTEDO L, et al. Layered LDGM codes: A capacityapproaching structure for arbitrary rates[C]//20074th International Symposium on Wireless Communication Systems. Trondheim, Norway: IEEE, 2007: 16-20. [21] HU X Y, ELEFTHERIOU E, ARNOLD D M. Regular and irregular progressive edge-growth tanner graphs[J]. IEEE Transactions on Information Theory, 2005, 51(1):386-398. doi: 10.1109/TIT.2004.839541 [22] TODD K M. Error correction coding: mathematical methods and algorithm[M].[S.l.]: Wiley_interscience, 2005. [23] ELKELESH A, EBADA M, CAMMERER S, et al. Improving belief propagation decoding of polar codes using scattered EXIT charts[C]//2016 IEEE Information Theory Workshop (ITW). Cambridge, UK: IEEE, 2016: 91-95. -


 ISSN
ISSN 




 下载:
下载: