ISSN 
下载:
-
近场源定位是阵列信号处理的主要问题之一。对于点源，当信号源距接收阵列较近时，平面波的假设不再成立，声波将以球面波的形式到达阵列。子空间方法实现近场源定位已有较多文献论述。例如，文献[1]将一维MUSIC算法推广为二维MUSIC算法用于近场源定位，文献[2-3]将高阶累积量应用到子空间方法中提高了定位精度。文献[4]采用对称阵列，将扩展ERSPRIT方法应用到近场源定位，且该方法将二维搜索转化为两次一维搜索，降低了计算量。文献[5]利用了信号的准平稳性得到了KR子空间，实现了准备平稳信号的欠定DOA估计。
近年来，稀疏重构理论逐渐应用到信号方向估计上。文献[6]提出了l1-SVD算法，将阵列多测量信号进行奇异值分解，得到信号子空间，然后约束噪声项和稀疏信号子空间的l1范数来完成信号源的定位。文献[7]建立协方差矩阵稀疏模型并应用于DOA。通过矢量化协方差矩阵的稀疏表示和互素阵列相结合的方法进行信号波达方向估计日益受到重视[8-12]。文献[9]从信号方向不在方向格点的角度，分析了互素阵列条件下接收信号协方差矩阵稀疏表示的DOA估计方法。文献[11-12]利用TV范数来求解稀疏问题得到DOA估计，文献[13-16]研究了宽带信号的欠定DOA估计问题。然而近场源的欠定估计问题还未深入研究。本文首先将基于KR积的子空间方法推广到近场源定位的欠定估计，然后重点研究了基于KR积的稀疏重构近场源定位方法。
-
考虑阵元数为$M$的均匀直线阵列，阵元间距为d，空间存在$K$个中心频率为${f_0}$的窄带信号入射到阵列，则第$m$个阵元接收到的信号可以表示为：
$$\begin{gathered} {x_m}(t) = \sum\limits_{k = 1}^K {{s_k}(t)} {{\rm{e}}^{{\rm{j}}2\pi {f_0}{\tau _m}({\theta _k}, {r_k})}} + {n_m}(t) \\ m = 1, 2, \cdots , M \\ \end{gathered} $$ (1) 式中，${s_k}(t)$第$k$个为信源；${n_m}(t)$是第$m$个阵元上的加性噪声，且噪声与信源不相关；${\tau _m}({\theta _k}, {r_k})$是第$m$个阵元与参考阵元接收到第$k$个声源信号的时间差；${\theta _k}$为第$k$个声源信号的方位角；${r_k}$为第$k$个声源信号到参考阵元的距离，${\tau _m}({\theta _k}, {r_k})$可由式(2)计算得到：
$${\tau _m}({\theta _k}, {r_k}) = \frac{{{r_{mk}} - {r_k}}}{c} = \frac{{{r_{mk}} - {r_k}}}{{\lambda {f_0}}}$$ (2) 式中，${r_{mk}}$为第$m$个阵元与参考阵元与第$k$个声源的距离，可由三角形余弦定理得：
$${r_{mk}} = \sqrt {{r_k}^2 - 2(m - 1)d{r_k}\sin {\theta _k} + {{[(m - 1)d]}^2}} $$ (3) 将式(3)进行泰勒级数展开，保留二次幂得[12]：
$$ {r_{mk}} \approx {r_k}\left\{ {1 + \left[ {\frac{{(m - 1)d}}{{{r_k}}}} \right]\sin {\theta _k} + \frac{1}{2}{{\left[ {\frac{{(m - 1)d}}{{{r_k}}}} \right]}^2}{{\cos }^2}{\theta _k}} \right\} $$ (4) 令${\alpha _k} = - 2\pi \frac{{d\sin {\theta _k}}}{\lambda }$，${\beta _k} = \pi \frac{{{d^2}{{\cos }^2}{\theta _k}}}{{{r_k}\lambda }}$，由式(1)、式(2)和式(3)得：
$${x_m}(t) = \sum\limits_{k = 1}^K {{s_k}(t)} {{\rm{e}}^{{\rm{j}}((m - 1){\alpha _k} + {{(m - 1)}^2}{\beta _k})}} + {n_m}(t)$$ (5) 令$\mathit{\boldsymbol{S}}(t) = {[{s_1}(t){\rm{ }}{s_2}(t){\rm{ }} \cdots {\rm{ }}{s_K}(t)]^{\rm{T}}}$，$\boldsymbol{X}(t) = [{x_1}(t){\rm{ }}$ ${x_2}(t){\rm{ }} \cdots {\rm{ }}{x_M}(t){]^{\rm{T}}}$，可写成矩阵形式：
$$\mathit{\boldsymbol{X}}(t) = \mathit{\boldsymbol{A}}(\theta ,r)\mathit{\boldsymbol{S}}(t) + \mathit{\boldsymbol{N}}(t)$$ (6) 其中：
$\mathit{\boldsymbol{A}}(\theta ,r) = [\mathit{\boldsymbol{a}}({\theta _1},{r_1}),\mathit{\boldsymbol{a}}({\theta _2},{r_2}), \cdots ,\mathit{\boldsymbol{a}}({\theta _K},{r_K})] \in {^{M \times K}}$$\mathit{\boldsymbol{a}}({\theta _k},{r_k}) = {\left[ {1,{{\rm{e}}^{j({\alpha _k} + {\beta _k})}}, \cdots ,{{\rm{e}}^{{\rm{j}}({\alpha _k}(M - 1) + {\beta _k}{{(M - 1)}^2})}}} \right]^{\rm{T}}} \in {^{M \times 1}}$
式中，$\mathit{\boldsymbol{A}}(\theta ,r)$为阵列的方向矩阵；$\mathit{\boldsymbol{a}}({\theta _k},{r_k})$为阵元接收到的第$k$个信号源的方向向量。
-
假设各信号源互不相关，且是准平稳的。各阵元处噪声互不相关。取一段信号分成$L$帧，帧长为$\Delta $。第$l$帧信号协方差矩阵定义为：
$${\mathit{\boldsymbol{R}}_l} = E\{ \mathit{\boldsymbol{X}}(t){\mathit{\boldsymbol{X}}^{\rm{H}}}(t)\} \;\forall t \in [(l - 1)\Delta ,l\Delta - 1]$$ (7) 假设各信源信号和噪声信号均为零均值准平稳信号，各信源信号互不相关，且从不同位置发出，此协方差矩阵可以表示为：
$${\mathit{\boldsymbol{R}}_l} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Z}}_l}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{C}}_l}$$ (8) 其中：
$${\mathit{\boldsymbol{Z}}_l} = {\rm{Diag}}({z_{l1}},{z_{l2}}, \cdots ,{z_{lK}})$$ $${\mathit{\boldsymbol{C}}_l} = {\rm{Diag}}({c_{l1}},{c_{l2}}, \cdots ,{c_{lM}})$$ 式中，${{\rm{z}}_{lk}} = {\rm{E}}\{ |{s_k}(t){|^2}\} $为第$k$个信号在第$l$帧时间段的信号功率；${{\rm{c}}_{lm}} = {\rm{E}}\{ |{n_k}(t){|^2}\} $为第$m$个阵元在第$l$帧时间的噪声功率。将${\mathit{\boldsymbol{R}}_l}$矢量化得：
$${\mathit{\boldsymbol{y}}_l} = {\rm{vec}}({\mathit{\boldsymbol{R}}_l}) = {\rm{vec}}(\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Z}}_l}{\mathit{\boldsymbol{A}}^{\rm{H}}}) + {\mathop{\rm vec}\nolimits} ({\mathit{\boldsymbol{C}}_l}) = ({\mathit{\boldsymbol{A}}^*} \odot \mathit{\boldsymbol{A}}){{\rm{z}}_l} + {\rm{vec}}({\mathit{\boldsymbol{C}}_l})$$ (9) 式中，$ \odot $表示KR积；${( \cdot )^{\rm{H}}}$表示共轭转置；${( \cdot )^ * }$表示共轭。
将$\{ {\mathit{\boldsymbol{y}}_l},l = 1,2, \cdots ,L\} $写到一起得到矩阵：
$$\mathit{\boldsymbol{Y}} = ({\mathit{\boldsymbol{A}}^*} \odot \mathit{\boldsymbol{A}})\mathit{\boldsymbol{Z}} + \mathit{\boldsymbol{C}}$$ (10) 其中：
$$\boldsymbol{Z} = {[{\boldsymbol{z}_1},{\boldsymbol{z}_2}, \cdots ,{\boldsymbol{z}_L}]^T} = \left[ \begin{array}{l} {z_{11}}\;{z_{12}}\; \ldots \;{z_{1K}}\\ {z_{21}}\;{z_{22}}\; \ldots \;{z_{2K}}\\ \; \vdots \;\;\;\; \vdots \;\;\; \ddots \;\;\; \vdots \\ {z_{L1}}\;{z_{L2}}\; \ldots \;{z_{LK}} \end{array} \right]$$ $$\boldsymbol{C} = {[{\boldsymbol{c}_1},{\boldsymbol{c}_2}, \cdots ,{\boldsymbol{c}_L}]^{\rm{T}}} = \left[ \begin{array}{l} {c_{11}}\;{c_{12}}\; \ldots \;{c_{1K}}\\ {c_{21}}\;{c_{22}}\; \ldots \;{c_{2K}}\\ \; \vdots \;\;\;\; \vdots \;\;\; \ddots \;\;\; \vdots \\ {c_{L1}}\;{c_{L2}}\; \ldots \;{c_{LK}} \end{array} \right]$$ 将Y进行奇异值分解得：
$$\mathit{\boldsymbol{Y}} = [{\mathit{\boldsymbol{U}}_s}\;{\mathit{\boldsymbol{U}}_c}]\left[ {\begin{array}{*{20}{l}} {{\mathit{\Sigma }_s}\;0}\\ {0\;\;\;{\mathit{\Sigma }_c}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{V}}_s^{\rm{H}}}\\ {\mathit{\boldsymbol{V}}_c^{\rm{H}}} \end{array}} \right]$$ (11) 式中，${\mathit{\boldsymbol{U}}_s}$和$\mathit{\boldsymbol{V}}_s^{\rm{H}}$分别是是由大奇异值对应的左右奇异值矢量张成的子空间，也就是信号子空间；${\mathit{\boldsymbol{U}}_s}$和$\mathit{\boldsymbol{V}}_s^{\rm{H}}$是由小奇异值对应的左右奇异值矢量张成的子空间，也就是噪声子空间；${\mathit{\Sigma }_s}$是由大奇异值组成的对角线矩阵；${\mathit{\Sigma }_c}$是由小奇异值组成的对角线矩阵。
由此得信源的方向向量满足：
$$\mathit{\boldsymbol{U}}_c^{\rm{H}}[{\mathit{\boldsymbol{a}}^*}({r_p},{\theta _p}) \otimes {\mathit{\boldsymbol{a}}^*}({r_p},{\theta _p})] = 0$$ 式中，$\mathit{\boldsymbol{a}}({r_p},{\theta _p})$为第p个声源信号的方向向量；$ \otimes $表示Kronecker积。
信号源空间谱可写为：
$$ \mathit{\boldsymbol{P}}{\rm{ = }}1/\mathit{\boldsymbol{U}}_c^{\rm{H}}[{\mathit{\boldsymbol{a}}^*}({r_p},{\theta _p}) \otimes {\mathit{\boldsymbol{a}}^*}({r_p},{\theta _p})]\; $$ (12) 如果各阵元处噪声是平稳的，则第$m$个阵元处各帧时间段的噪声功率相等，即：
$${c_{1m}} = {c_{2m}} = \cdots = {c_{Lm}}$$ 式(7)可以写为：
$$\mathit{\boldsymbol{Y}} = ({\mathit{\boldsymbol{A}}^*} \odot \mathit{\boldsymbol{A}})\mathit{\boldsymbol{Z}} + {\rm{vec}}({\mathit{\boldsymbol{C}}_l})\mathit{\boldsymbol{1}}_L^{\rm{T}}$$ (13) 式中，${\mathit{\boldsymbol{1}}_L} = {[1,2, \cdots ,1]^{\rm{T}}}$
可以通过${{\bf{1}}_\mathit{L}}$的正交投影矩阵$\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot $消除噪声，正交投影矩阵为：
$$\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot = {{\rm{I}}_L} - (1/L){\mathit{\boldsymbol{1}}_L}\mathit{\boldsymbol{1}}_L^{\rm{T}}$$ 所以：
$$\mathit{\boldsymbol{YP}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot = ({\mathit{\boldsymbol{A}}^*} \odot \mathit{\boldsymbol{A}}){(\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot {\mathit{\boldsymbol{Z}}^{\rm{T}}})^{\rm{T}}} + {\rm{vec}}({\mathit{\boldsymbol{C}}_l})\mathit{\boldsymbol{1}}_L^{\rm{T}}\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot = ({\mathit{\boldsymbol{A}}^*} \odot \mathit{\boldsymbol{A}}){(\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{1}}_L}}^ \bot {\mathit{\boldsymbol{Z}}^{\rm{T}}})^{\rm{T}}}{\rm{ }}$$ (14) 再利用子空间方法求出空间谱。
-
假设信号源可能的方位角为$\Theta = ({\widetilde \theta _1}, {\widetilde \theta _2}, \cdots , $ ${\widetilde \theta _P})$，可能的距离为$R = ({\widetilde r_1}, {\widetilde r_2}, \cdots , {\widetilde r_Q})$，则信源可能的位置可离散化为$H = P \times Q$个点，且$K \ll H$，那么接收矩阵Y可以稀疏表示为：
$$\mathit{\boldsymbol{Y}} = ({\mathit{\boldsymbol{\widetilde A}}^*} \odot \mathit{\boldsymbol{\widetilde A}})\mathit{\boldsymbol{\widetilde Z}} + \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{\widetilde B}}\mathit{\boldsymbol{\widetilde Z}} + \mathit{\boldsymbol{C}}$$ (15) $$\begin{matrix} \widetilde{\mathrm{\boldsymbol{B}}}=\left[ \begin{align} & {{\mathrm{\boldsymbol{a}}}^{*}}({{\widetilde{\theta }}_{1}},{{\widetilde{r}}_{1}})\otimes \mathrm{\boldsymbol{a}}({{\widetilde{\theta }}_{1}},{{\widetilde{r}}_{1}}),{{\mathrm{\boldsymbol{a}}}^{*}}({{\widetilde{\theta }}_{2}},{{\widetilde{r}}_{1}})\otimes \mathrm{\boldsymbol{a}}({{\widetilde{\theta }}_{2}},{{\widetilde{r}}_{1}}),\cdots , \\ & {{\mathrm{\boldsymbol{a}}}^{*}}({{\widetilde{\theta }}_{P}},{{\widetilde{r}}_{Q}})\otimes \mathrm{\boldsymbol{a}}({{\widetilde{\theta }}_{P}},{{\widetilde{r}}_{Q}}) \\ \end{align} \right] \\ \in {{\mathbb{C}}^{M\times H}} \\ \end{matrix}$$ $${\widetilde \alpha _p} = - 2\pi \frac{{d\sin {{\widetilde \theta }_p}}}{\lambda }, {\widetilde {{\rm{ }}\beta }_{pq}} = \pi \frac{{{d^2}{{\cos }^2}{{\widetilde \theta }_p}}}{{{r_q}\lambda }}$$ $$\begin{gathered} a({\widetilde \theta _p}, {\widetilde r_q}) = \\ \left[ {1, {{\rm{e}}^{{\rm{j}}({{\widetilde \alpha }_p} + {{\widetilde \beta }_{pq}})}}, {\operatorname{e} ^{{\rm{j}}(2{{\widetilde \alpha }_p} + 4{{\widetilde \beta }_{pq}})}}, \cdots , {{\rm{e}}^{{\rm{j}}({{\widetilde \alpha }_p}(M - 1) + {{\widetilde \beta }_{pq}}{{(M - 1)}^2})}}} \right] \\ h = 1, 2, \cdots , H, P \in [1, P], q \in [1, Q] \\ \end{gathered} $$ 对Y进行奇异值分解可得：
$$\mathit{\boldsymbol{Y}}{\rm{ = }}{\mathit{\boldsymbol{U}}_o}{\mathit{\boldsymbol{L}}_o}\mathit{\boldsymbol{V}}_o^{\rm{T}}\;\;$$ 式中，L中的奇异值从左上角到右下角按从大到小排列；Y保存前K列可得到$\mathit{\boldsymbol{Y}}{\rm{ = }}{\mathit{\boldsymbol{U}}_o}{\mathit{\boldsymbol{L}}_o}{\mathit{\boldsymbol{D}}_K} = \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{V}}_o}{\mathit{\boldsymbol{D}}_K}$，其中${\mathit{\boldsymbol{D}}_K}{\rm{ = }}[{\mathit{\boldsymbol{I}}_K}\;{\mathit{\boldsymbol{0}}^{\rm{T}}}]$。${\mathit{\boldsymbol{I}}_\mathit{K}}$为$K \times K$维单位矩阵，$\mathit{\boldsymbol{0}}$为$K \times (T - K)$维零矩阵。令：
$${\mathit{\boldsymbol{C}}_{SV}}{\rm{ = }}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{V}}_o}{\mathit{\boldsymbol{D}}_K}$$ $$ {\mathit{\boldsymbol{Z}}_{SV}}{\rm{ = }}\mathit{\boldsymbol{\widetilde Z}}{\mathit{\boldsymbol{V}}_o}{\mathit{\boldsymbol{D}}_K} = {[z_1^{SV}\; \cdots \;z_H^{SV}]^{\rm{T}}} $$ $$\mathit{\boldsymbol{z}}_i^{SV} = {\left[ {z_i^{SV}(1)\;z_i^{SV}(2)\; \cdots \;z_i^{SV}(K)} \right]^{\rm{T}}}\;\;i = 1,2, \cdots ,H$$ 可得：
$${\mathit{\boldsymbol{Y}}_{{\rm{SV}}}}{\rm{ = }}\mathit{\boldsymbol{\widetilde B}}{\mathit{\boldsymbol{Z}}_{{\rm{SV}}}}{\rm{ + }}{\mathit{\boldsymbol{C}}_{{\rm{SV}}}}$$ (16) 可得优化目标函数为：
$$\mathop {\min }\limits_S \left\| {{\mathit{\boldsymbol{Y}}_{{\rm{SV}}}} - \mathit{\boldsymbol{\widetilde B}}{\mathit{\boldsymbol{Z}}_{{\rm{SV}}}}} \right\|_{\rm{F}}^2 + \lambda {\left\| {{\mathit{\boldsymbol{z}}^{SV({l_2})}}} \right\|_1}$$ (17) 其中：
${\mathit{\boldsymbol{z}}^{SV({{l}_{2}})}}=\left[ z{{_{1}^{SV}}^{({{l}_{2}})}}z{{_{2}^{SV}}^{({{l}_{2}})}}\cdots z{{_{H}^{SV}}^{({{l}_{2}})}} \right]z{{_{i}^{SV}}^{({{l}_{2}})}}=\sqrt{\sum\limits_{k=1}^{K}{z_{i}^{SV}(k)}}$
问题(17)可转化为二阶锥规划问题：
$$\min p + \lambda q$$ (18) $$ \begin{matrix} \text{s}\text{.t}\ \left\| {{\text{Y}}_{\text{SV}}}-\widetilde{\text{B}}{{\text{Z}}_{\text{SV}}} \right\|_{f}^{2}\le p \\ {1}'r\le q \\ z{{_{i}^{SV}}^{({{l}_{2}})}}\le r(i)\ \text{ }i=1, 2, \cdots , P \\ \end{matrix} $$ 通过求解上面优化问题就可以得到信号的位置估计。此问题是二阶锥规划问题，可通过文献[17]中的CVX软件来求解。
-
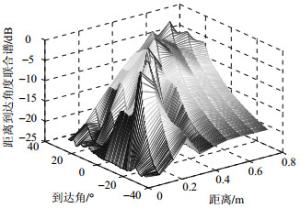
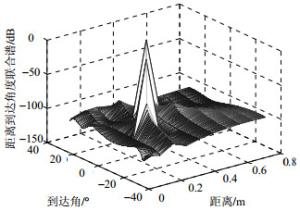
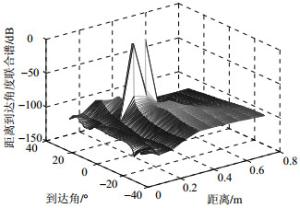
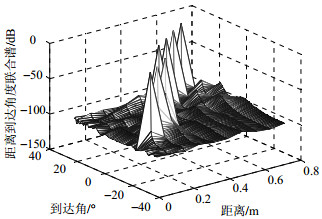
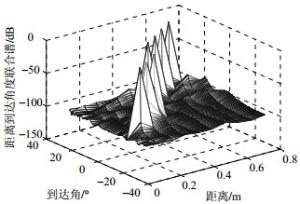
为简便称本文算法为KRSR(KHATRI-RAO sparse representation)，子空间定位方法称为KRmusic，用于KR子空间的capon方法称为KRcapon。以下实验将对3种算法的性能进行比较。取阵列阵元数为6，阵元间距为波长的四分之一。取6个声源，入射位置分别为：$( - 15^\circ , 0.142){\rm{, }}$ $( - 10^\circ {\rm{, }}$ $0.222){\rm{, }}$$( - 5^\circ , 0.302){\rm{, }}$$({\rm{10}}^\circ , 0.382){\rm{, }}({\rm{1}}5^\circ {\rm{, }}0.462){\rm{, }}$ $({\rm{20}}^\circ {\rm{, }}$ $0.542){\rm{, }}$$(25^\circ , 0.622){\rm{, }}$取稀疏度参数$\lambda = 2.3$，采样点数为25 000，帧数为50，每帧为500点，噪声为高斯白噪声，信噪比分别为SNR=10 dB和SNR=0 dB时，声源的空间谱仿真如图 1~图 4所示。从图中可以看出，当信噪比SNR=10 dB时，KRSR算法谱峰优于KRmusic算法，但KRmusic算法仍可以清晰分辨各声源。当信噪比SNR=0 dB时KRSR算法的谱峰仍很明显，但KRmusic算法已经不能分辨声源。
图 1 SNR=10 dB时KRSR空间谱
图 2 SNR=10 dB时KRmusic空间谱
图 3 SNR=0 dB时KRSR空间谱
图 4 SNR=0 dB时KRmusic空间谱
为了验证本文算法的分辨率能力，将两个声源从$(11^\circ , 0.302)$和$({\rm{12}}^\circ , 0.382)$位置阵列，信噪比SNR=15 dB。仿真结果如图 5和图 6所示，KRmusic方法此时已经几乎不能分辨两个角度，KRSR算法仍能明显分辨各入射信号。
图 5 SNR=15 dB时两声源入射KRSR空间谱
图 6 SNR=15 dB时两声源入射KRmusic空间谱
将两个声源从$( - 9^\circ , 0.222)$和$({\rm{12}}^\circ , 0.382)$位置阵列，信噪比SNR=15 dB。相干声源的空间谱估计仿真结果如图 7和图 8所示，可以看出KRmusic方法不能分辨两个声源，KRSR算法仍能明显分辨入射信号。
图 7 SNR=0 dB时两相干声源入射KRSR空间谱
图 8 SNR=0 dB时两相干声源入射KRSR空间谱
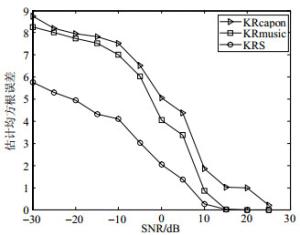
最后讨论算法的误差性能与信噪比及帧数的关系。仿真结果如图 9和图 10所示，分别显示了误差性能受信噪比和采样点数的影响。从图中可以看出，KRSR算法误差性能均优于其他两种。
图 9 3种方法均方根误差与SNR关系
图 10 3种方法均方根误差与帧数关系
-
针对信源数多于阵元数的情况，本文首先将KHATRI-RAO子空间方法扩展到近场源定位方法，接着提出一钟基于KHATRI-RAO变换的稀疏重构近场源定位方法。该方法通过KR积变换得到阵列输出信号的KHATRI-RAO子空间，然后在KHATRI-RAO子空间对信号进行了稀疏表示，从而通过l1范数约束求得声源的空间谱，实现声源的欠定定位。仿真结果表明，此方法的定位性能与基于KHATRI-RAO子空间近场源定位方法相比有较大的提高。
本文工作得到河南师范大学博士启动课题(qd18027)的资助，在此表示感谢。
Near-Field Sound Source Localization via Sparse Reconstruction Based on KR Product
-
摘要: 针对声源数多于阵元数的近场信源定位问题，该文提出一种基于Khatri-Rao（KR）积的稀疏重构近场源定位方法。该方法首先假设信号是准平稳的，然后通过KR积得到虚拟阵列结构，增加了阵列的自由度；接着在虚拟阵列结构下对虚拟信号进行稀疏表示，最后通过l1范数约束得到声源的空间谱估计。仿真表明，此稀疏重构定位方法可以实现信源定位的欠定估计，且性能优于基于KR积的子空间方法。Abstract: Aiming at the problem of near-field sound source localization estimation under the condition of less array elements than sources, the method of sparse reconstruction based on Khatri-Rao (KR) product is proposed. The source signals are wide-sense quasi-stationary in this method. A virtual array structure is acquired by KR product and the degree of freedom is increased. In the virtual array structure the spectra of the sound sources are acquired band on sparse reconstruction, which is solved by l1 norm method. Simulations demonstrate the proposed method can realized underdeterminded estimation of sound source and the performance is better than the subspace method.
-
Key words:
- KR product /
- l1 norm /
- near-field /
- source localization /
- sparse reconstruction
-
[1] HUANG Y D, BARKAT M. Near-field mutiple sources localization by passive sensor array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(7):968-975. doi: 10.1109/8.86917 [2] YUEN N, FRIEDLANDER B. Performance analysis of higher order ESPRIT for localization of near-field sources[J]. IEEE Transactions on Signal Processing, 1998, 46(3):709-719. doi: 10.1109/78.661337 [3] CHALLA R N, SHAMSUNDER S. High-order subspace based algorithms for passive localization of near-field sources[C]//Proceedings of the 29th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, California, USA: IEEE, 1995: 777-781. [4] ZHI W, CHIA M Y. Near-field source localization via symmetric subarrays[J]. IEEE Signal Processing Letters, 2007, 14(6):409-412. doi: 10.1109/LSP.2006.888390 [5] MA W K, HSIEH T H, CHI C Y. DOA estimation of Quasi-stationary signals with less sensors than sources and unknown spatial noise covariance:A Khatri-Rao subspace approach[J]. IEEE Transactions on Signal Processing, 2010, 58(4):2168-2180. doi: 10.1109/TSP.2009.2034935 [6] MALIOUTOV D, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8):3010, 3022. doi: 10.1109/TSP.2005.850882 [7] YIN J, CHEN T. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J]. IEEE Transactions on Signal Processing, 2011, 59(9):4489-4493. doi: 10.1109/TSP.2011.2158425 [8] ZHANG Y D, AMIN M G, HIMED B. Sparsity-based DOA estimation using co-prime arrays[C]//International Conference Acoustics, Speech, Signal Process (ICASSP). Vancouver, BC, Canada: IEEE, 2013: 3967-3971. [9] ZHAO Tan, NEHORAI A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets[J]. IEEE Signal Processing Letters, 2014, 21(1):26-29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c6e172febddb91c4b21162e61d697153 [10] ZHANG Y D, QIN S, AMIN M G. DOA estimation exploting coprime arrays with sparse sensor spacing[C]//International Conference Acoustics, Speech, and Signal Process (ICASSP). Florence, Italy: IEEE, 2014: 2267-2271. [11] ZHAO Tan, NEHORAI A, ELDAR Y C. Continuous sparse recovery for direction of arrival estimation with co-prime arrays[C]//8th IEEE in Sensor Array and Multichannel Signal Processing Workshop (SAM).[S.l.]: IEEE, 2014: 393-396. [12] TAN Z, ELDAR Y C, NEHORAI A. Direction of arrival estimation using co-prime arrays:A super resolution viewpoint[J]. IEEE Trans Signal Process, 2014, 62(21), 5565-5576. doi: 10.1109/TSP.2014.2354316 [13] HE Zhen-qing, LIU Qing-hua, OUYANG Shan. Direction-of-arrival estimation with multiple-dictionary joint sparse representation via wideband covariance matrix[J]. Journal of Signal Processing, 2012, 28(5):686-691. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xhcl201205011 [14] ZHAO Guang-hui, LIU Zi-cheng, LIN Jie, et al. Wideband DOA estimation based on sparse representation in 2-D frequency domain[J]. IEEE Sensors Journal, 2015, 15(1):227-233. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=68d698c3c9eb41e45159c10f2eb916ef [15] SHEN Qing, LIU Wei, CUI Wei, et al. Group sparsity based wideband DOA estimation for co-prime arrays[C]//2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP). Xi'an, : China: IEEE, 2014, 23(9): 252-256. [16] HE Zhen-qing, SHI Zhi-ping, HUANG Lei, et al. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting[J]. IEEE Signal Processing Letters, 2015, 22(4):435-439. doi: 10.1109/LSP.2014.2358084 [17] GRANT M, BOYD S. CVX: Matlab software for disciplined convex programming[EB/OL].[2017-05-23]. Available: http://stanfordedu/~boyd/cvx. -
点击查看大图
图(10)
计量
- 文章访问数: 4277
- HTML全文浏览量: 1474
- PDF下载量: 64
- 被引次数: 0
