-
鲸鱼优化算法(WOA)是文献[1]提出的一种新元启发式优化算法,其原理是模仿座头鲸的狩猎策略,将座头鲸的狩猎行为演化成随机优化的过程。目前,许多研究学者将WOA算法应用到不同的工程领域,文献[2]提出一种局部搜索策略的混合鲸鱼算法,用于解决排列流水车间调度问题,得到高效率的调度策略。文献[3]提出了多目标鲸鱼算法(MOWOA),用来优化Elman中性网络的权重和阈值,可以更好地预测风速对电网的影响。文献[4]引入惯性权重策略来改进鲸鱼优化算法,在求解水资源分配模型时取得了很好的优化结果。文献[5]将鲸鱼算法和人工神经网络结合起来,用于求解Ad-hoc网络中的最优路径问题。文献[6]提出了一种随机的鲸鱼算法(SWO)来解决发电机组调度问题,实验证明SWO算法可以得到更低的燃料成本。文献[7]将鲸鱼优化算法应用于识别垃圾邮件发送者的社交网络。文献[8]提出了一种混合鲸鱼粒子群优化(HWPSO)算法优化电力系统,实验表明HWPSO算法的性能最佳。文献[9]将鲸鱼算法应用到最优无功率调度问题上,通过实验与粒子群算法进行比较,证明了鲸鱼算法在解决ORPD问题方面的稳健性和有效性。然而在求解高维多目标复杂工程问题时,WOA算法也存在收敛精度不高,易陷入局部最优解等问题。
为了改善WOA的优化性能,本文提出了一种离散鲸鱼优化算法(DWOA),在DWOA算法中引入收敛因子调节个体距离最优鲸鱼位置的远近程度,在最优位置附近进行更加精细的局部搜索,提高算法的局部寻优能力;此外,在鲸鱼个体位置更新公式中引入自适应惯性权值来协调算法的全局探索和局部开发能力,进一步改善算法的优化性能;最后利用改进的Sigmoid函数对WOA进行离散化处理保证了个体的多样性。对改进效果进行仿真验证,并将DWOA与其他8种优化算法在求解油田措施规划模型上进行对比,DWOA取得了很好的寻优效果。
-
鲸鱼优化算法(WOA)是模拟座头鲸的狩猎行为而构建的数学模型,寻优过程主要由包围猎物、泡泡网捕食和随机捕食3部分组成。
1) 包围猎物
座头鲸在捕食过程中,可以识别猎物的位置并包围它们。WOA算法模拟该行为时,以当前最优个体为参照,其他鲸鱼个体将它们的位置向最优个体位置的方向更新,此行为表示为:
式中,
$t$ 代表当前迭代次数;${{A}}$ 和${{C}}$ 是系数向量;${{{X}}^*}(t)$ 代表最优解的位置向量;${{X}}(t)$ 是位置向量;${{D}}$ 表示两者之间的距离。如果有更好的解决方案,则应在每次迭代中更新${{{X}}^*}(t)$ 。向量
${{A}}$ 和${{C}}$ 的公式为:式中,
$\alpha $ 在迭代过程中从2~0线性递减;${{\varUpsilon}}$ 为[0,1]随机数组成的向量。2) 泡泡网捕食
座头鲸在围攻猎物时,收缩包围的同时也在沿螺旋形路径运动。在优化过程中,假设收缩包围机制和螺旋位置机制的更新概率相同,都设置为0.5。用数学模型模拟座头鯨的泡泡网捕食行为的收缩包围机制和螺旋更新位置机制,有:
式中,
${{D}}' = \left| {{{{X}}^*}(t) - {{X}}(t)} \right|$ ;$p$ 为[0, 1]随机概率;$l$ 为[−1, 1]随机概率;b为定义螺旋形状的常数。3) 随机捕食
随机捕食与泡泡网捕食不同之处在于该阶段不是根据当前获得的最优个体,而是根据随机选择的鲸鱼个体作为参照鲸鱼来更新其他鲸鱼个体的位置,随机捕食的数学模型如下:
式中,
${{{X}}_{{\rm{rand}}}}$ 是一个随机位置向量。随机捕食设定了当系数变量$\left| {{A}} \right| \geqslant 1$ ,随机选择鲸鱼个体作为参照鲸鱼,以此来寻找其他更合适的猎物以增强算法的搜索捕食能力,使该算法能在全局范围内进行搜索。 -
1) 进化方式改进原理
标准的WOA算法在进行全局搜索的过程中,鲸鱼的位置是随机更新的,不能有效地平衡全局搜索和局部开发。为了提高鲸鱼算法的寻优能力,本文引入了自适应惯性权值
$w$ 来调节算法的全局搜索能力,有助于算法跳出局部最优。在迭代初期,应给予较大的惯性权值,保证算法的全局搜索能力,而在迭代后期,为了保证算法的局部搜索能力,应给予较小的惯性权值,进而平衡WOA算法在优化过程中的全局探索和局部开发能力。利用$w$ 的动态线性变化来控制鲸鱼位置对新鲸鱼位置的影响,改进后的更新公式为:式中,
$w$ 是惯性权值;${w_{\min }}$ 是惯性权值最小值;$t$ 是当前迭代数;${T_{\max }}$ 为最大迭代次数。进化理论研究表明,优秀的解周围很大程度上存在更多潜在优秀的解。标准WOA算法在迭代中进行局部搜索时,所有鲸鱼会逐渐向最优鲸鱼的位置移动,因此很大可能使得所有鲸鱼位于局部最优位置附近,算法只能在局部最优解附近搜索,不能寻找到更优的解。为了提高WOA算法的局部搜索能力,本文提出一种非线性收敛因子,通过收敛因子
$V$ 可以更好地调控最优解位置与其他个体之间的距离,发掘更多的潜在优秀解。使算法在进行局部开发时,可以在最优值附近更加全面精细地搜索优秀解,改进之后的位置矢量为:式中,
${v_{\min }}$ 表示收敛因子的最小值;${v_{\max }}$ 表示收敛因子的最大值;${\rm{rand}}$ 表示0~1之间的随机数;向量${{D}}$ 表示个体距离最优解位置之间的远近程度。2) 鲸鱼算法离散化原理
鲸鱼算法优化空间的值都是连续变量,但在实际工程应用中所计算的变量都是离散的,因此要对连续变量进行离散化处理。本文提出一种离散二进制鲸鱼算法编码方式,利用映射函数完成对鲸鱼算法的离散化。在迭代过程中,为了保证个体的位置只能为0或1,通常使用Sigmoid函数[10-11]将位置压缩到[0,1]区间来表示个体取1的概率,其公式为:
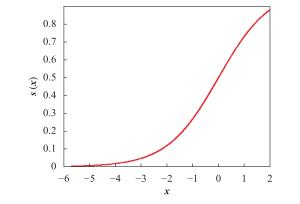
Sigmoid函数的核心是将连续搜索空间映射到离散搜索空间,利用标准Sigmoid函数对鲸鱼个体位置映射的结果如图1所示。从图1可以看出,映射结果大都集中在0.5~0.76之间,若用式(14)对映射结果离散化处理,个体容易产生“靠拢”现象,会使算法过早收敛,陷入局部最优。
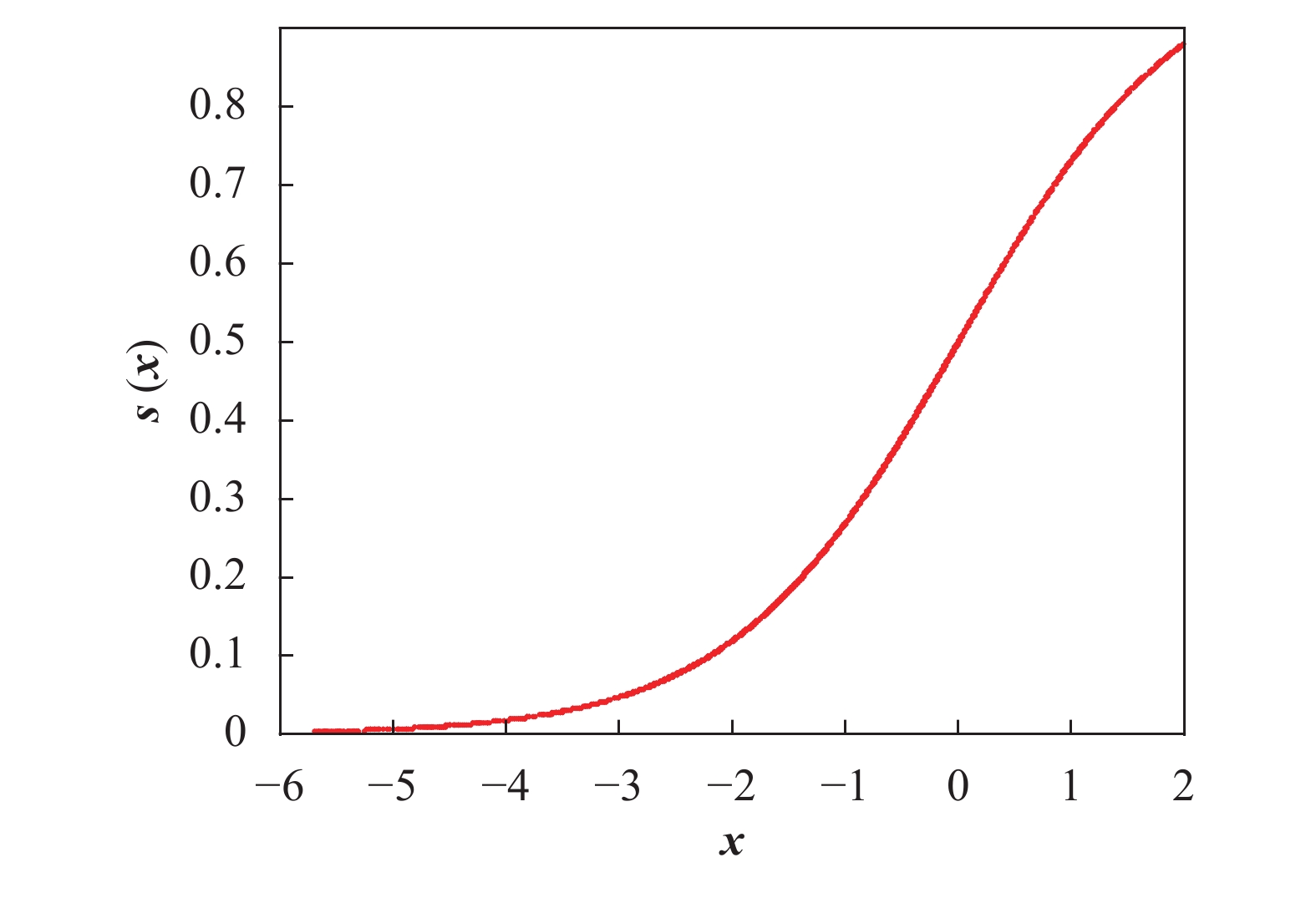
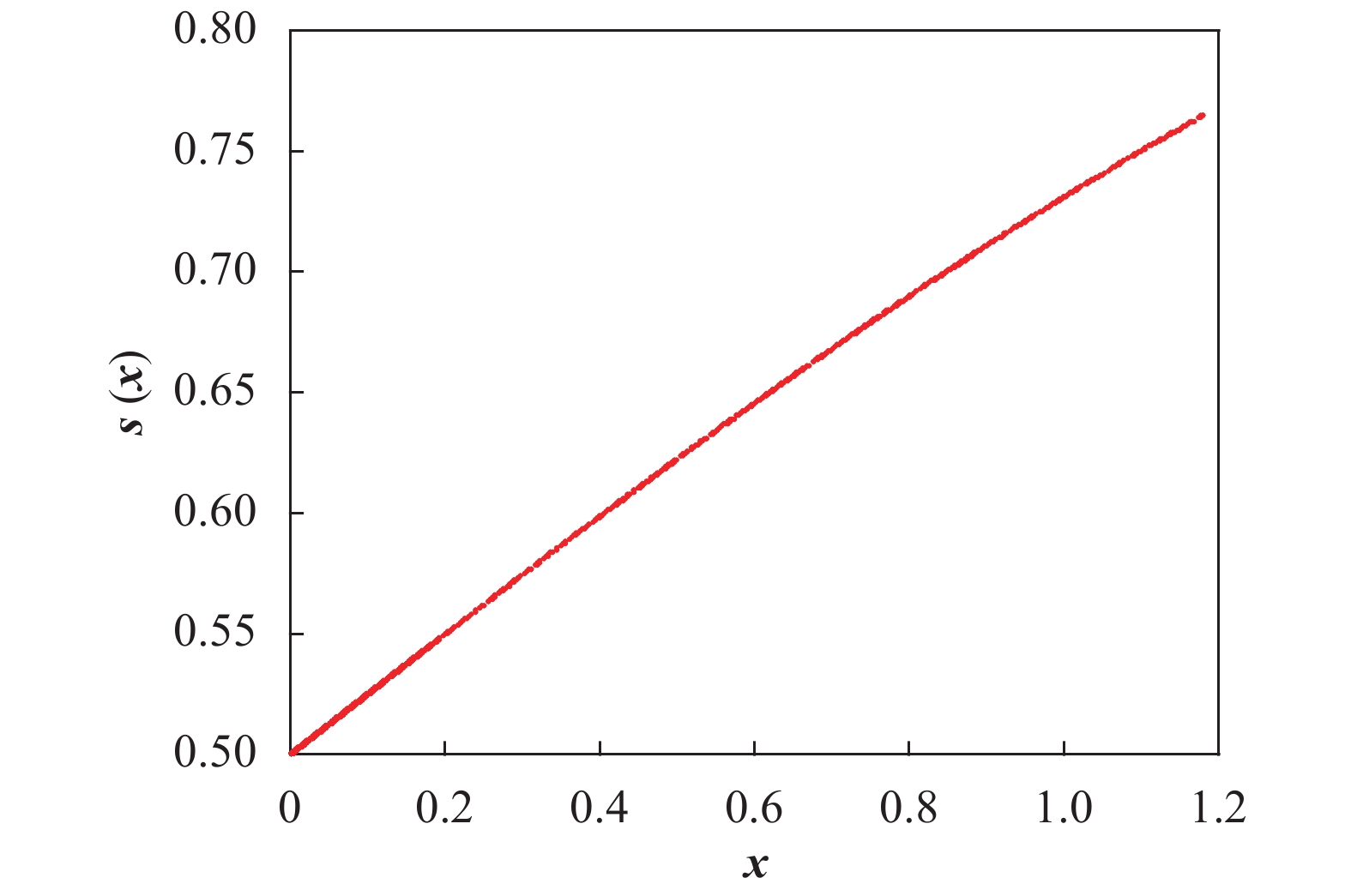
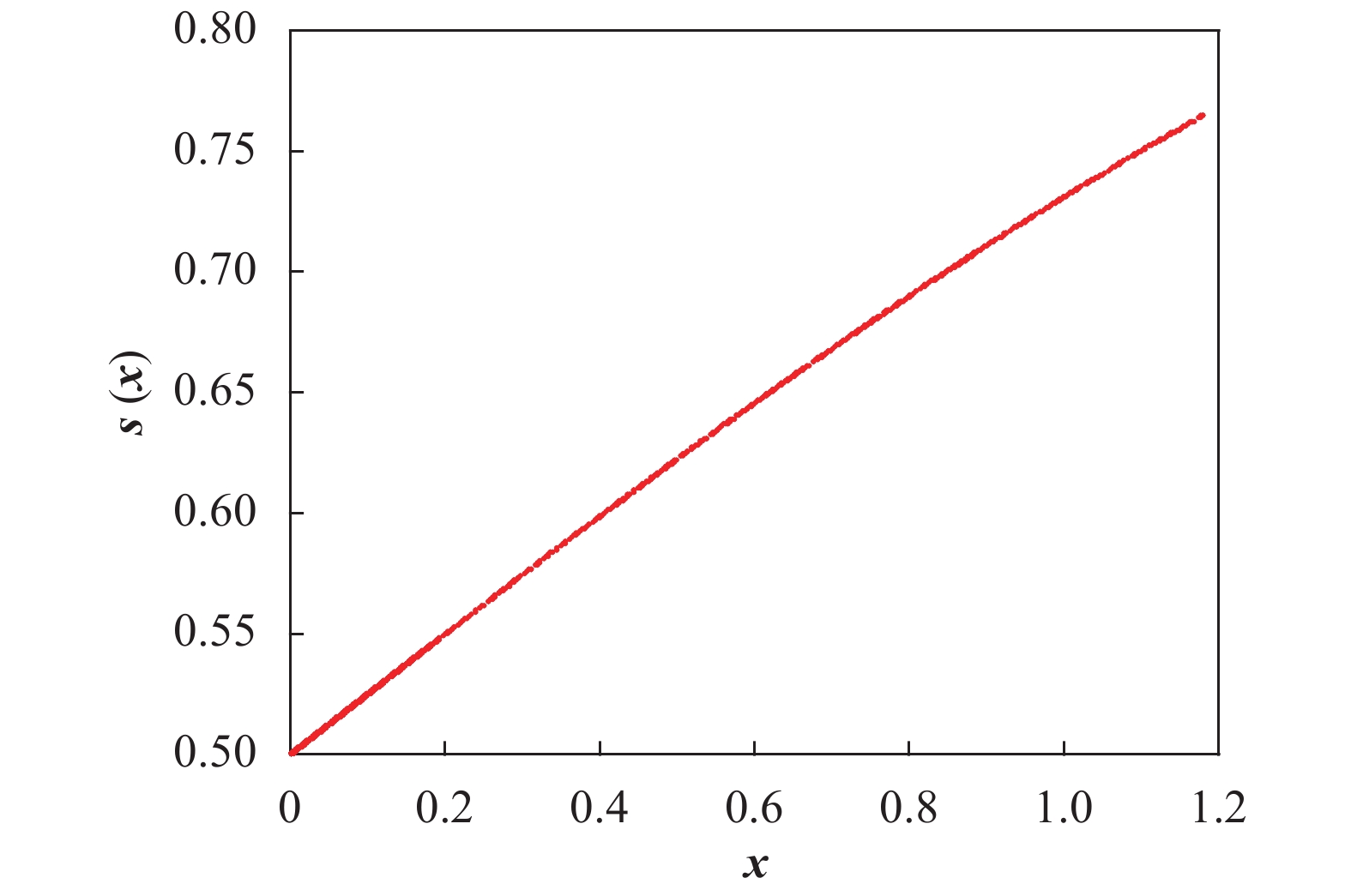
为了提高算法的搜索能力,本文通过对最优位置和个体位置的差值进行映射改进Sigmoid函数的映射公式,映射结果如图2所示。
可以看出,映射结果值分布在0~0.9之间,更好地保证了离散化后个体的多样性,为算法的优化过程奠定了多样性基础。改进后的Sigmoid函数为:
式中,
${{{x}}^*}$ 为当前最优个体;${{x}}$ 为位置向量;${\rm{VarSize}}$ 是维数大小。 -
DWOA的具体操作步骤为:
1) 初始化鲸鱼种群
${{{x}}_i}$ ($i = 1,2, \cdots ,Q$ ),计算每个个体${{{x}}_i}$ 的适应度值$F$ ,得到初始最优位置${{{x}}^*}$ 、最优解${F^{\rm{*}}}$ ,当前迭代次数$t = 0$ ,最大迭代次数为${T_{{\rm{max}}}}$ ;2)
$ {\rm{while }}\;t < {T_{{\rm{max}}}}$ 3)
$ {\rm{for }}\;i = 1:Q$ 4) 应用式(3)、式(4)更新参数
$\alpha ,{{A}},{{C}},l$ ,p;5)
$ {\rm{if }}\;p < 0.5$ 6)
$ {\rm{if }}\;\left| {{A}} \right| < 1$ 7) 应用式(10)~式(12)更新策略得到新个体
${{x}}_i^{{\rm{new}}}$ ;8)
$ {\rm{else \;if }}\;\left| {{A}}\right| \geqslant 1$ 9) 应用式(1)、式(8)和式(9)更新策略得到新个体
$ {{x}}_i^{{\rm{new}}}$ ;10)
${\rm{end \;if}}$ 11)
$ {\rm{else \;if }}\;p \geqslant 0.5$ 12) 应用式(10)~式(12)更新策略得到新个体
${{x}}_i^{{\rm{new}}}$ ;13)
$ {\rm{end \;if}}$ 14) 应用式(15)、式(16)对更新后的个体
${{x}}_i^{{\rm{new}}}$ 进行离散化处理,将其值映射到[0,1]区间;15)
$ {\rm{if \;rand}} < {{s}}({{x}}_i^{{\rm{new}}})$ 16)
$ {{x}}_i^{{\rm{new}}} = 1$ ;17)
${\rm{else}}$ 18)
$ {{x}}_i^{{\rm{new}}} = 0$ ;19)
$ {\rm{end \;if}}$ 20)
$ {\rm{end \;for}}$ 21) 计算每个新鲸鱼个体
${{x}}_i^{{\rm{new}}}$ 的适应度值${F^{{\rm{new}}}}$ ;22)
$ {\rm{if }}\;{F^{{\rm{new}}}}\;{\rm{ better \;than }}\;{F^*}$ 23)
$ {{{x}}^*} = {{x}}_i^{{\rm{new}}}$ ;24)
${F^*} = {F^{{\rm{new}}}}$ ;25)
$ {\rm{end\; if}}$ 26)
$ {\rm{end \;while}}$ -
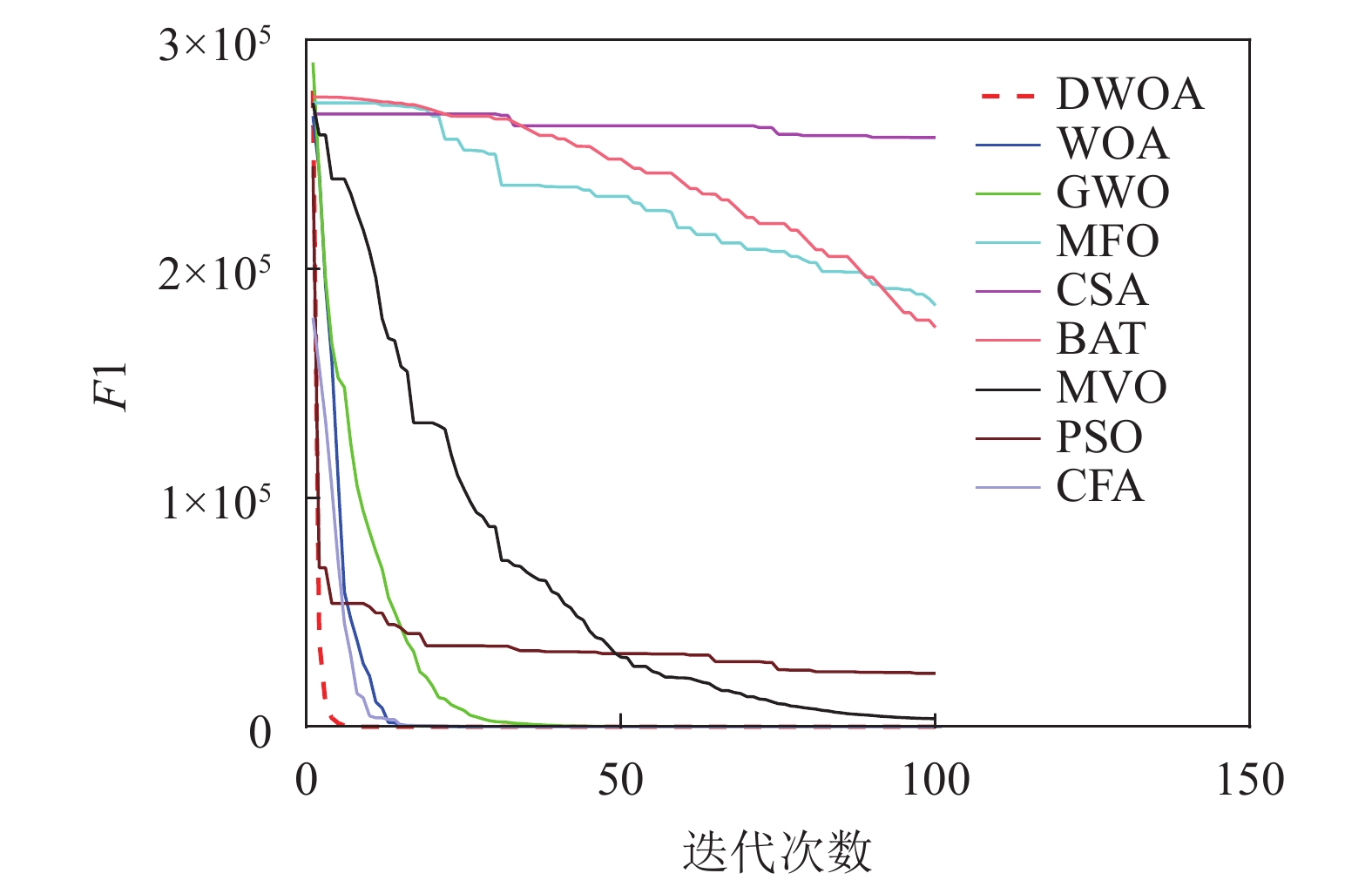
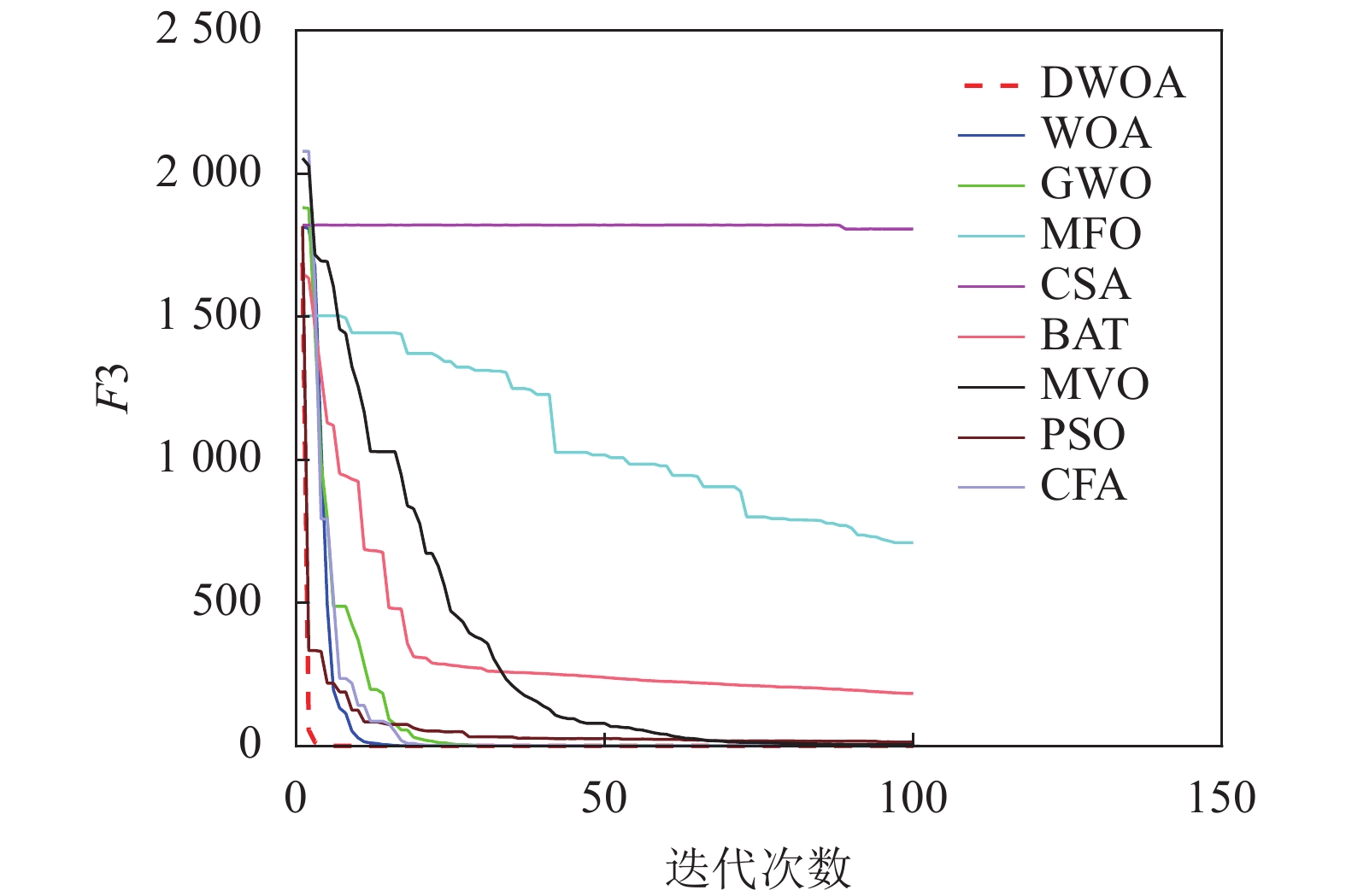
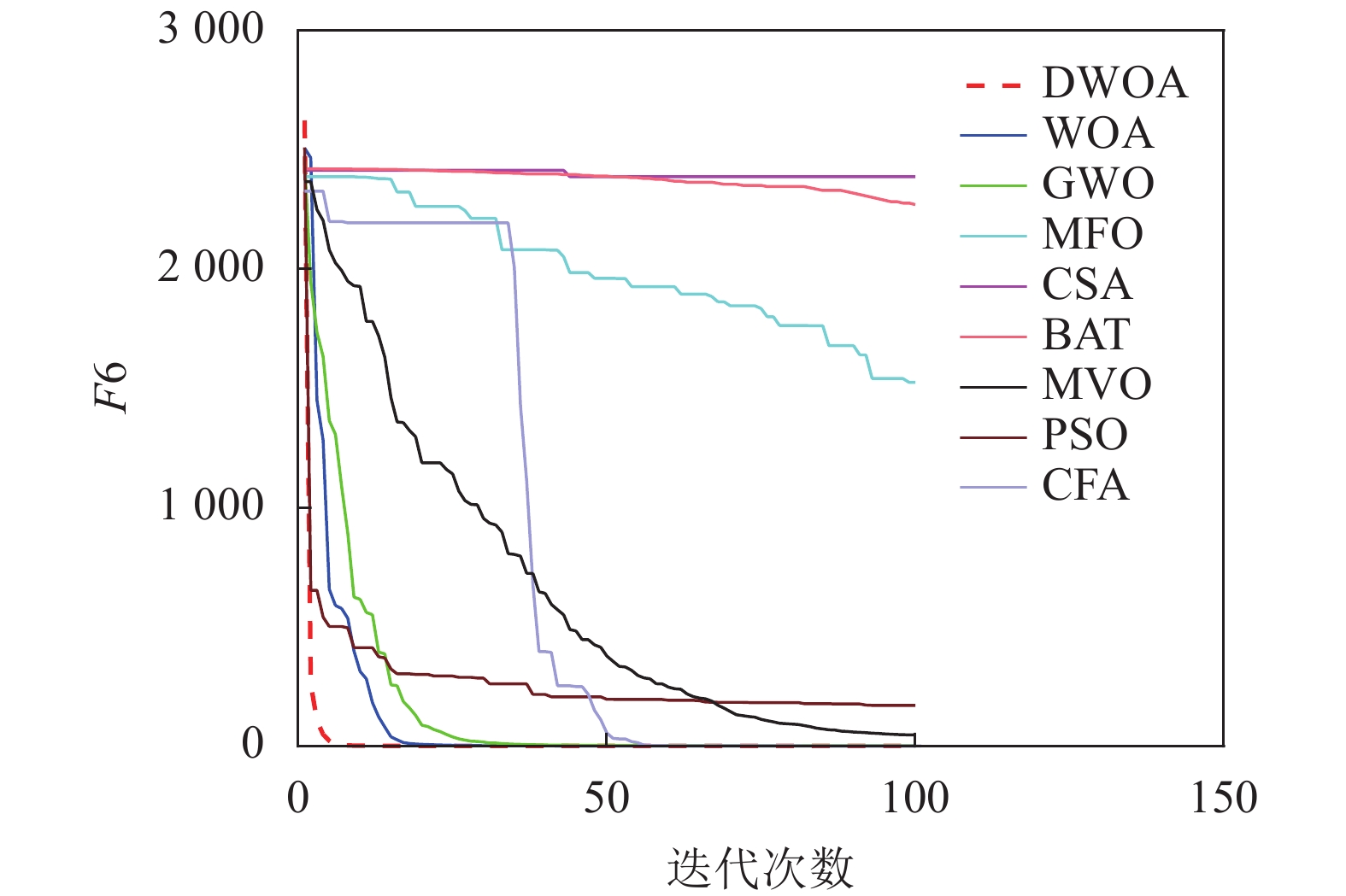
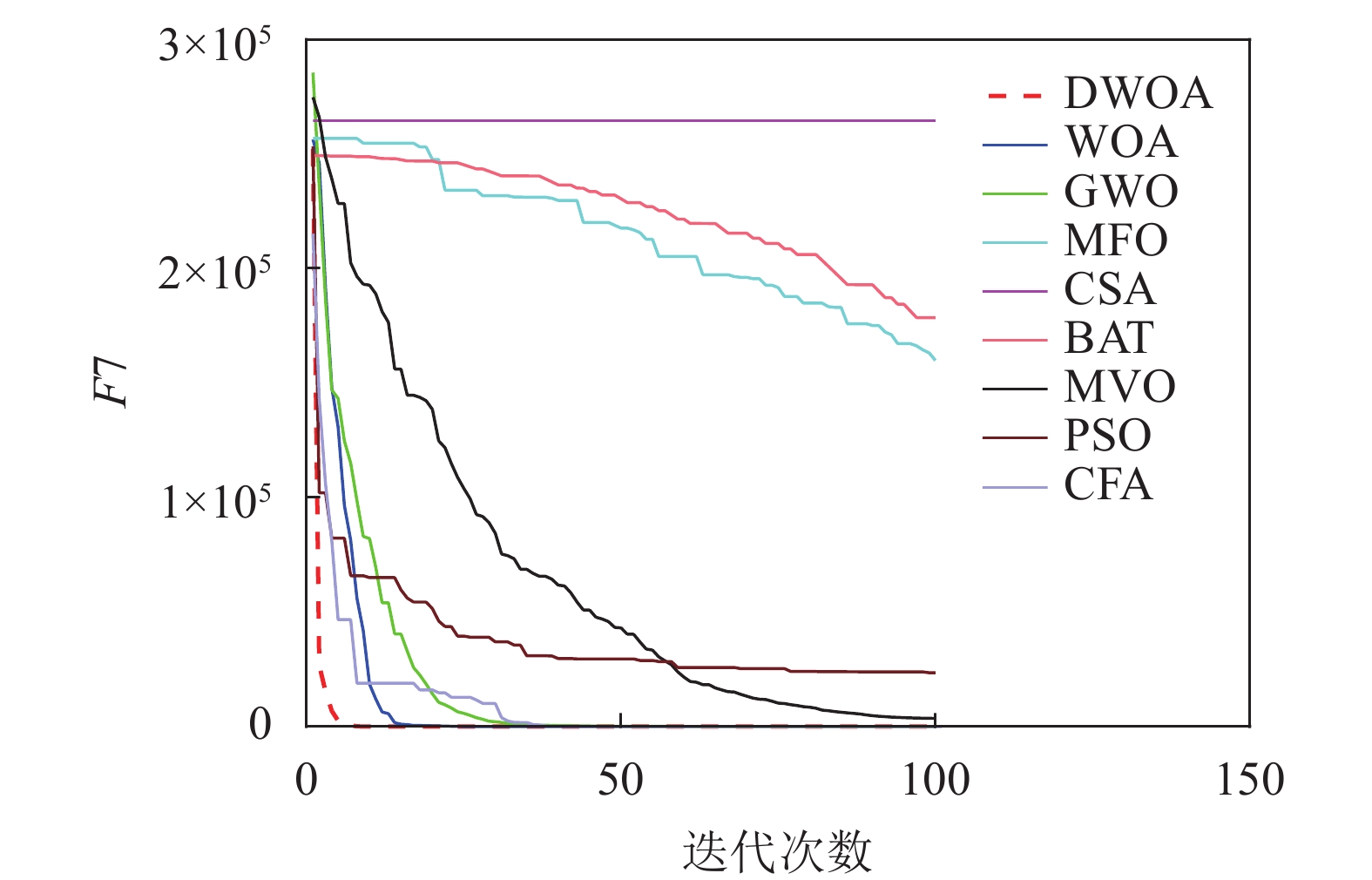
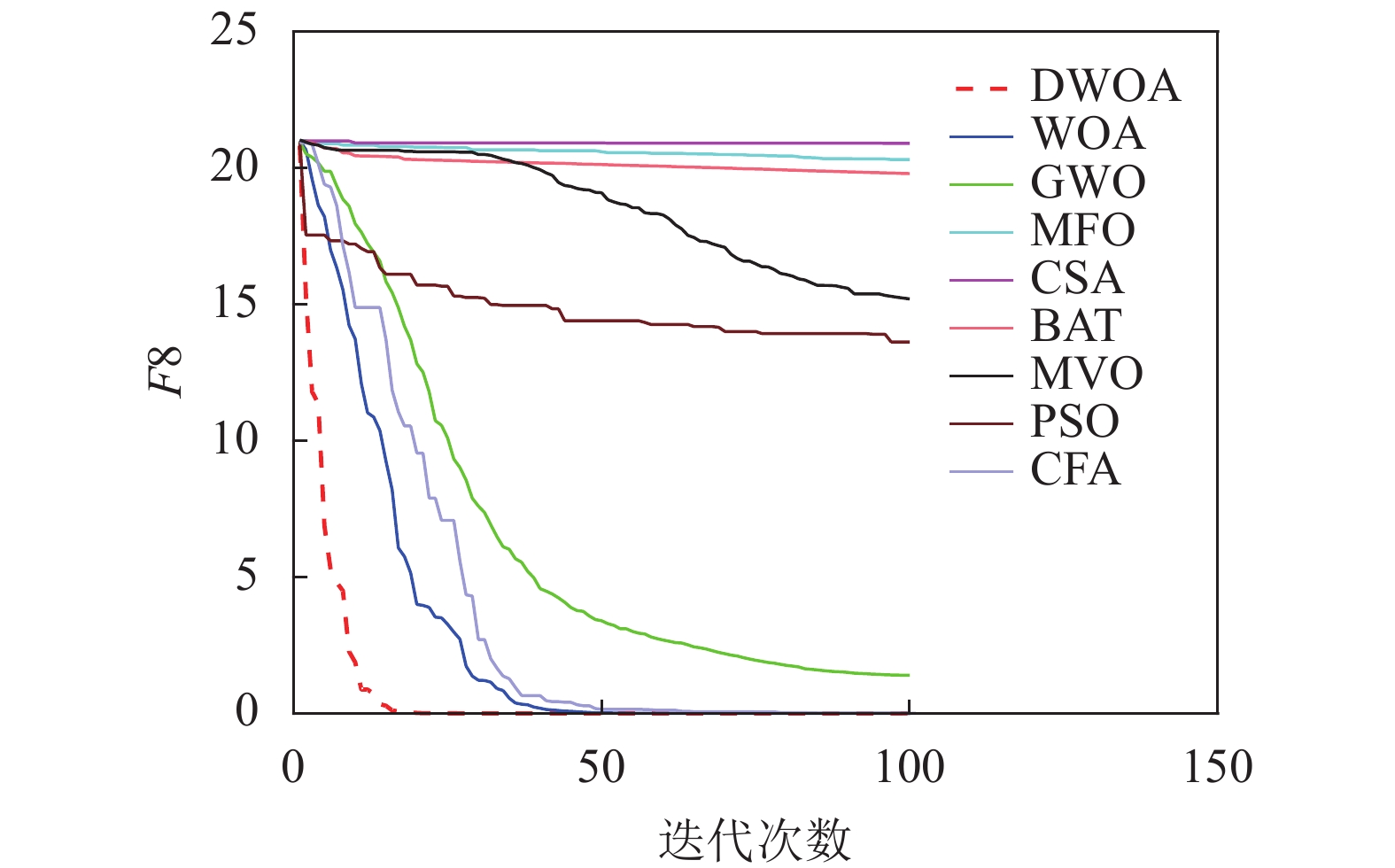
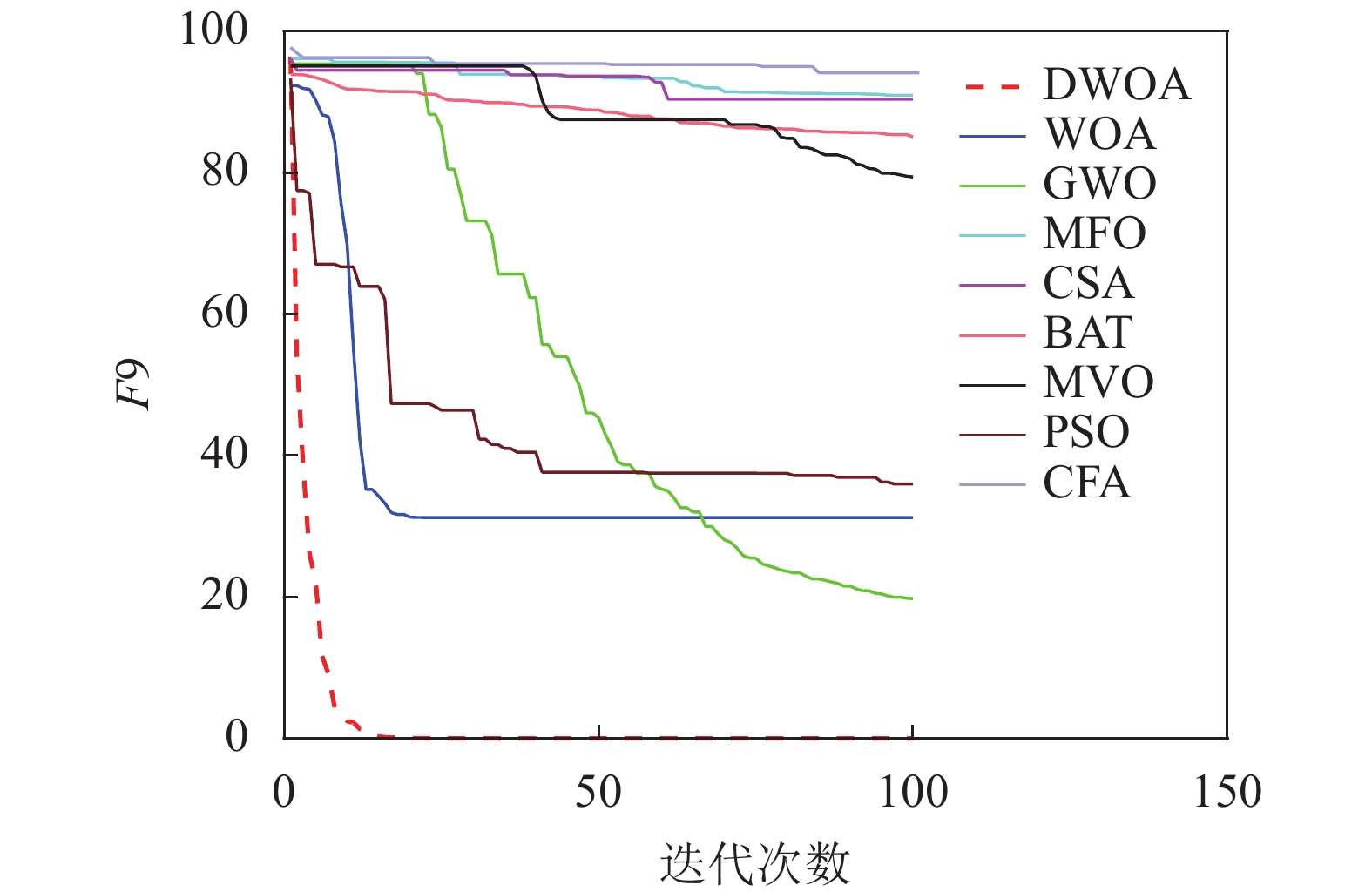
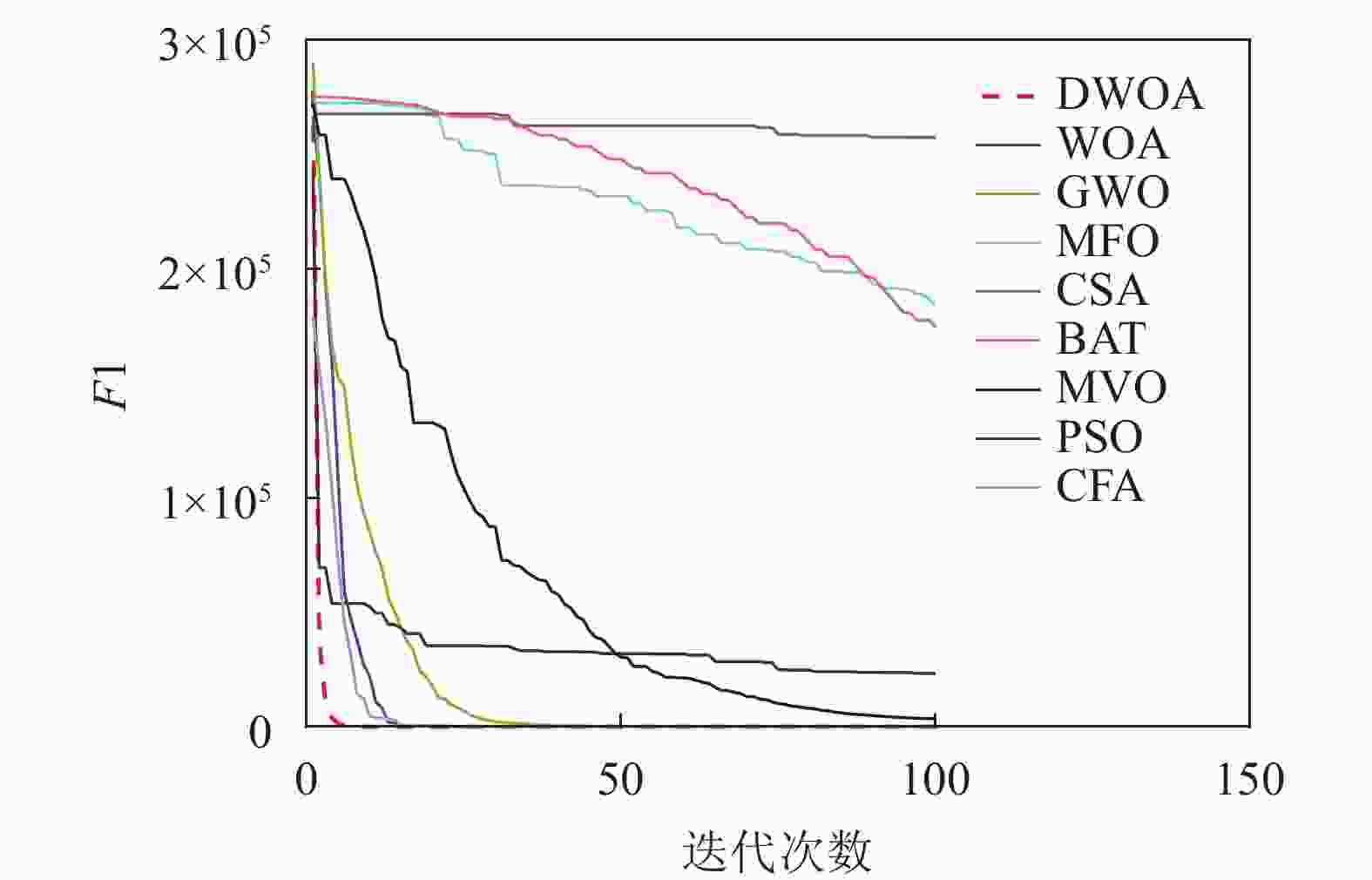
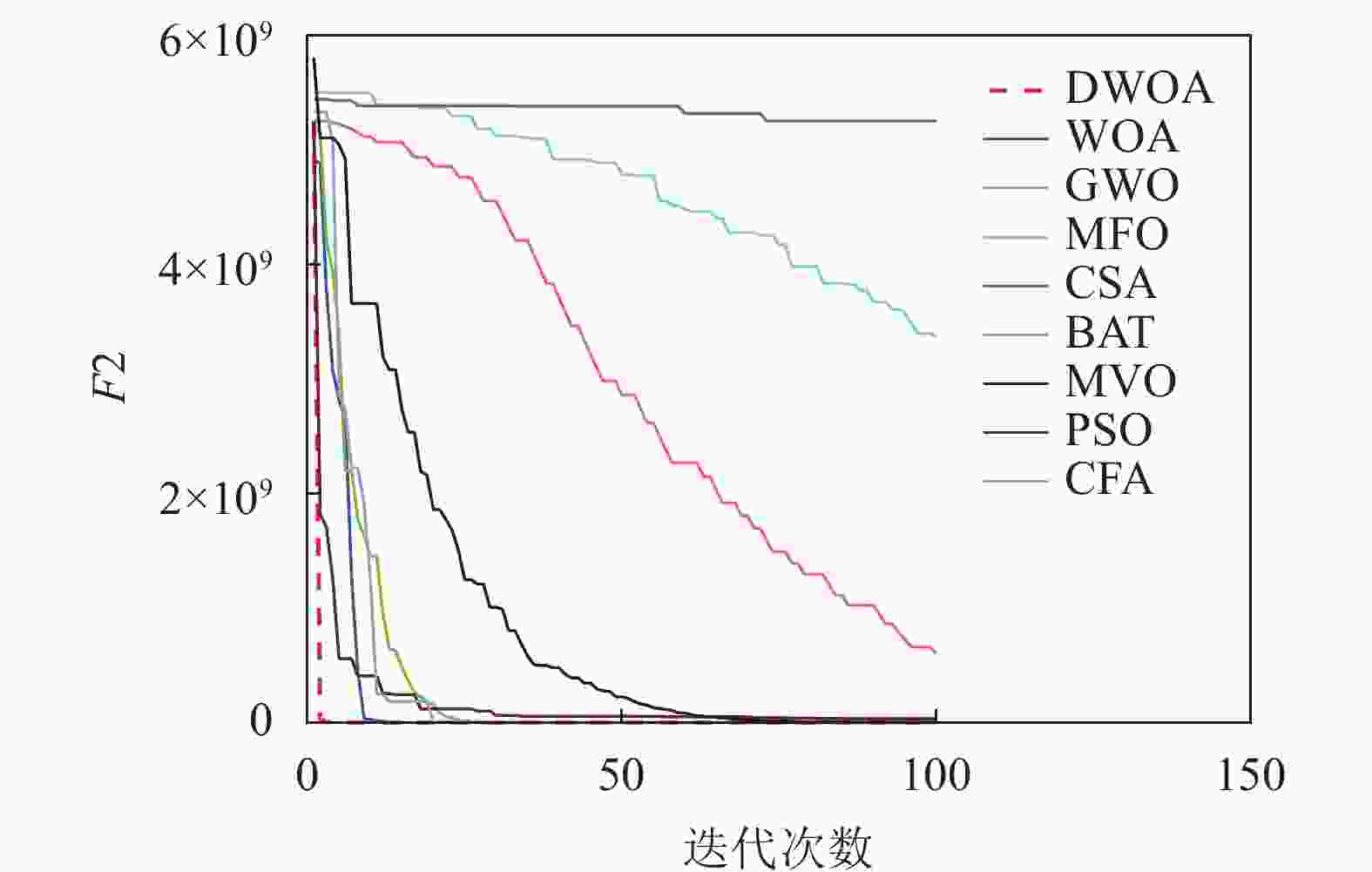
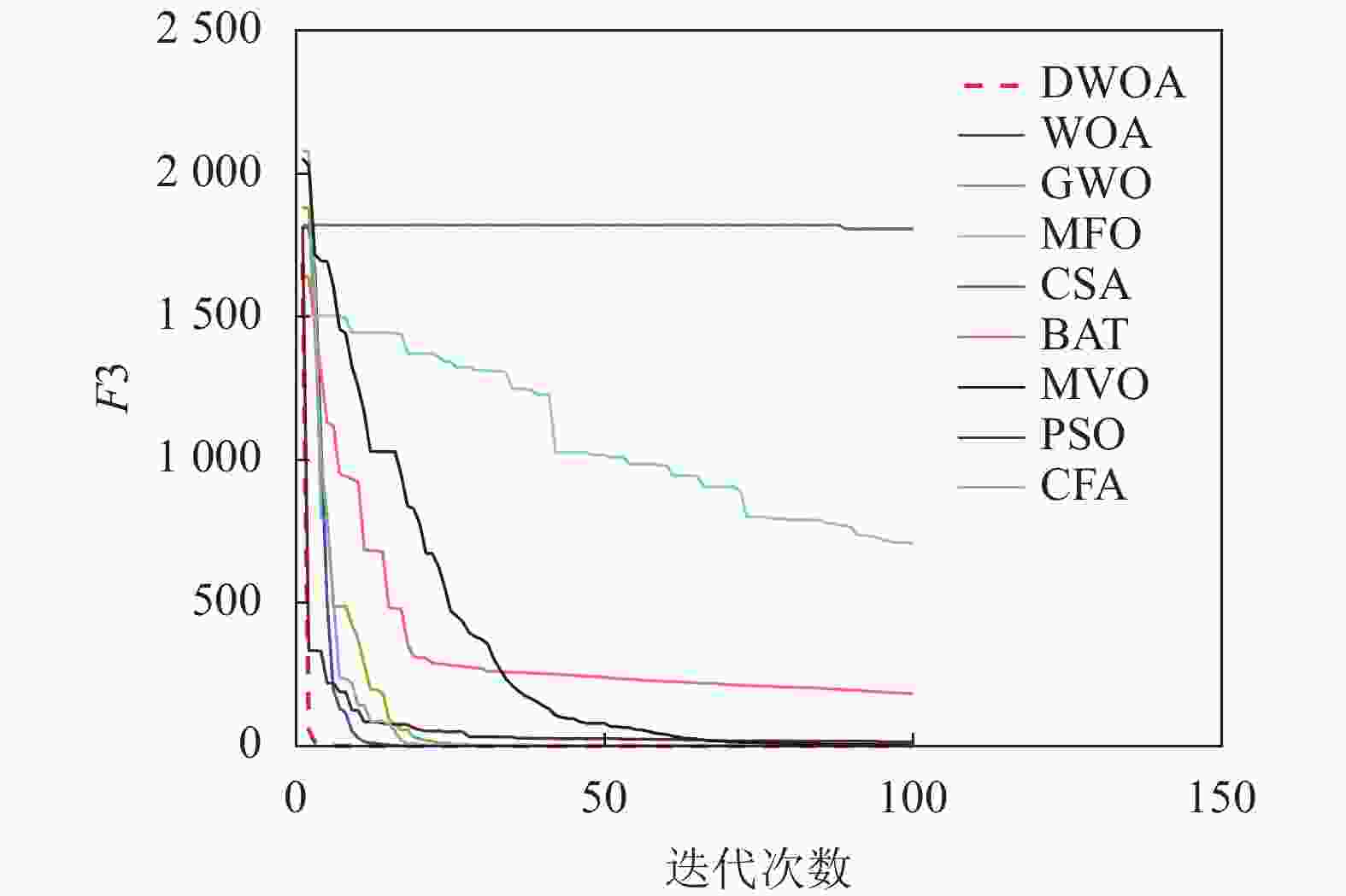
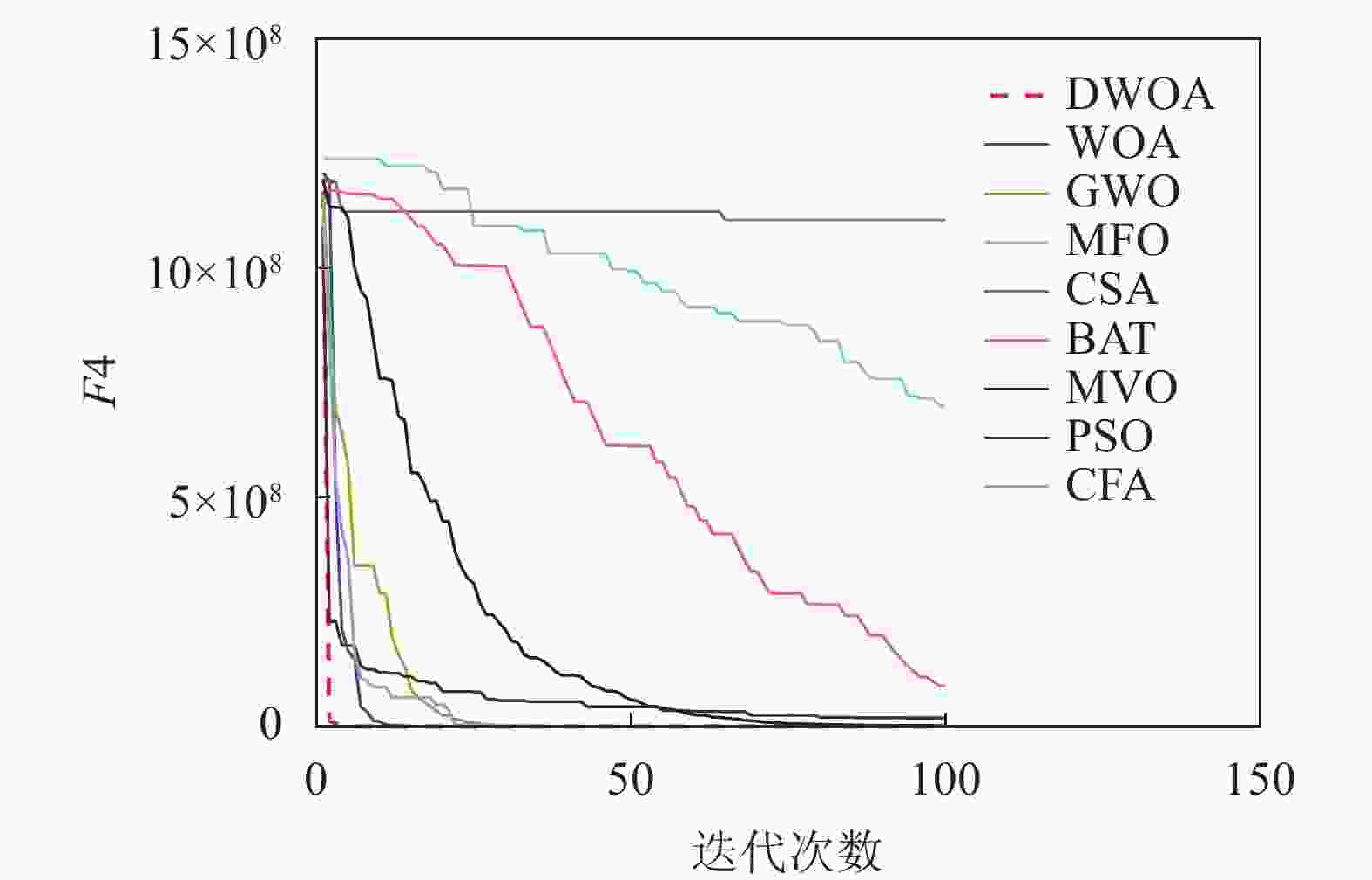
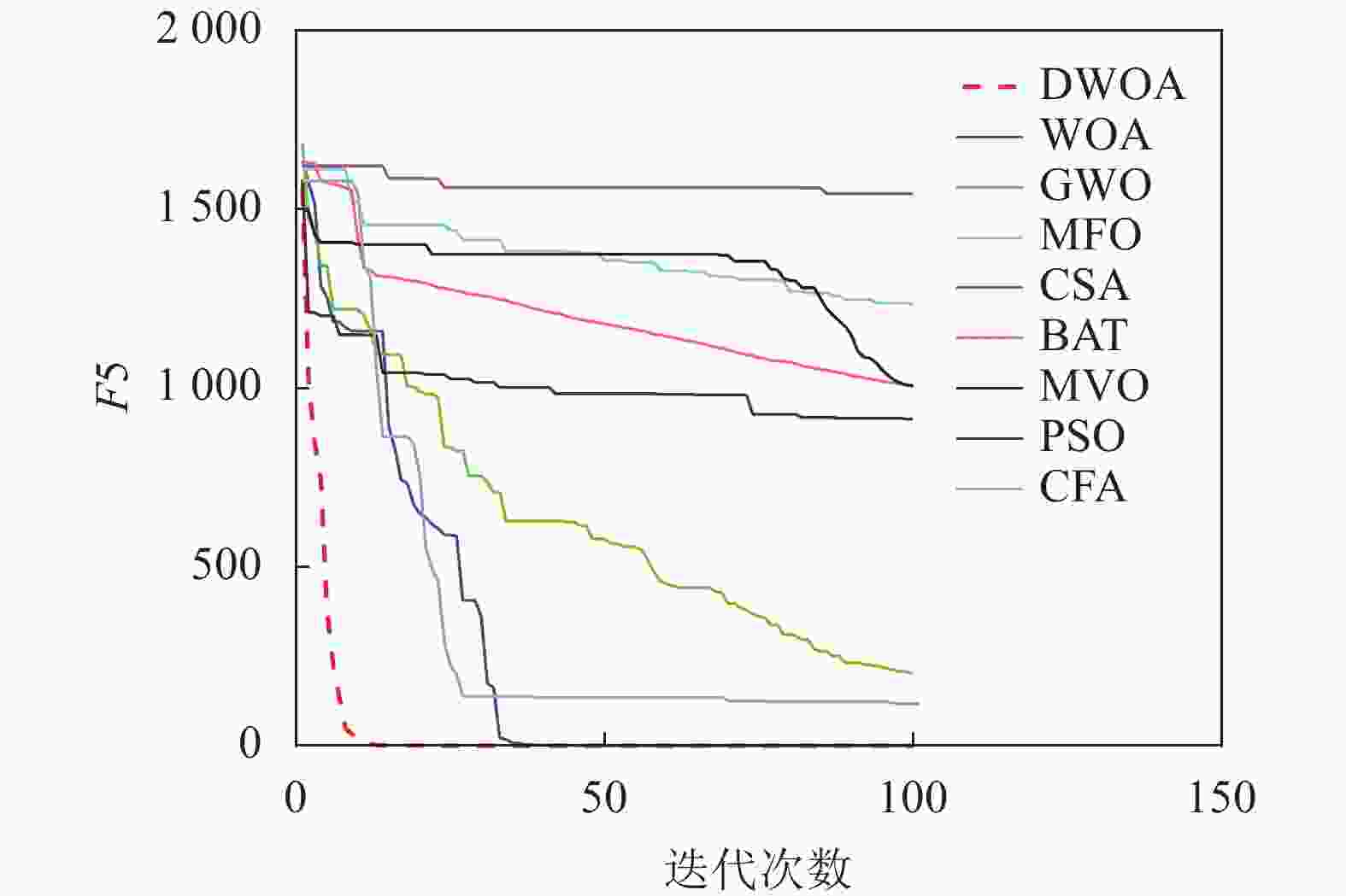
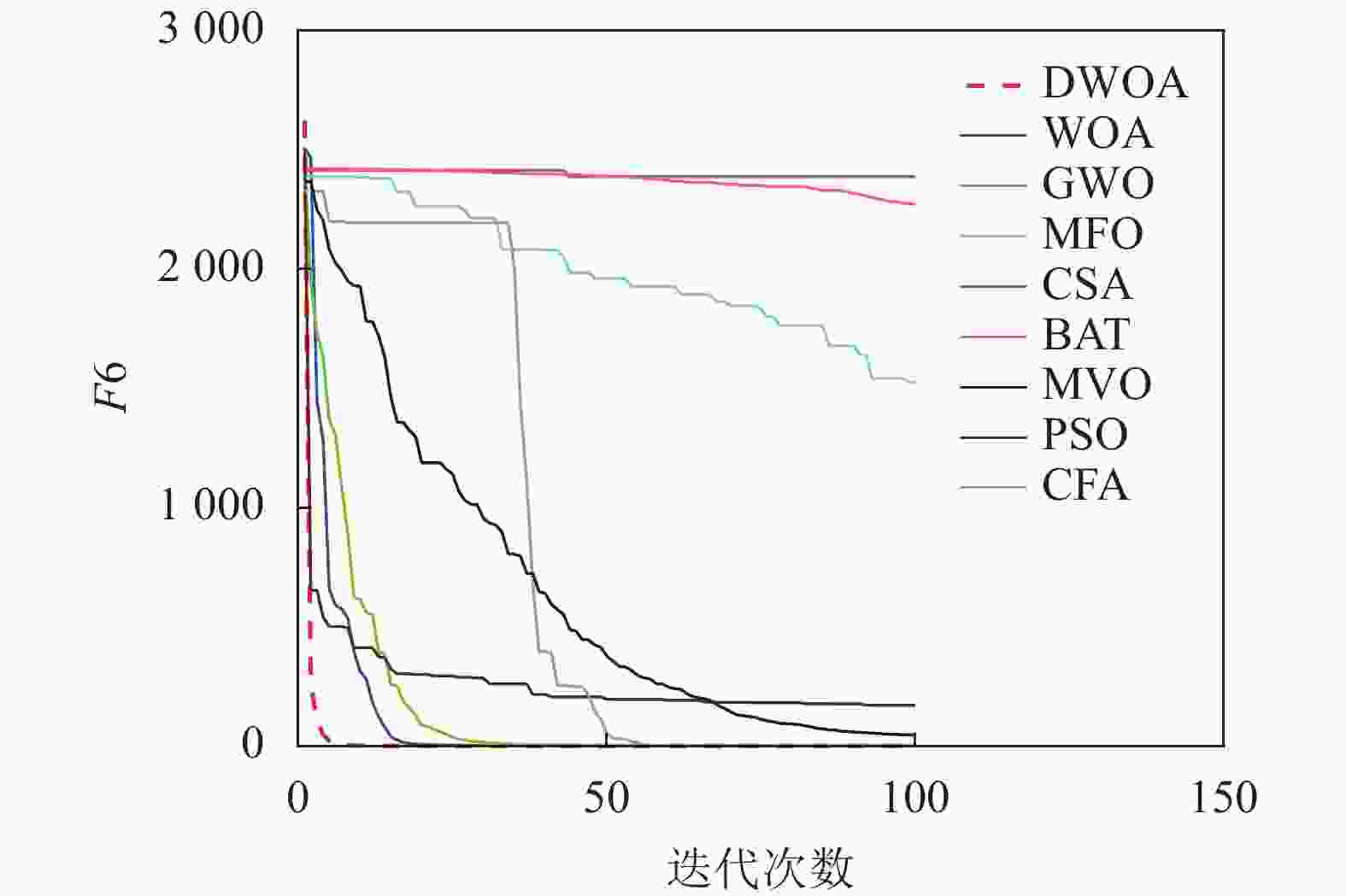
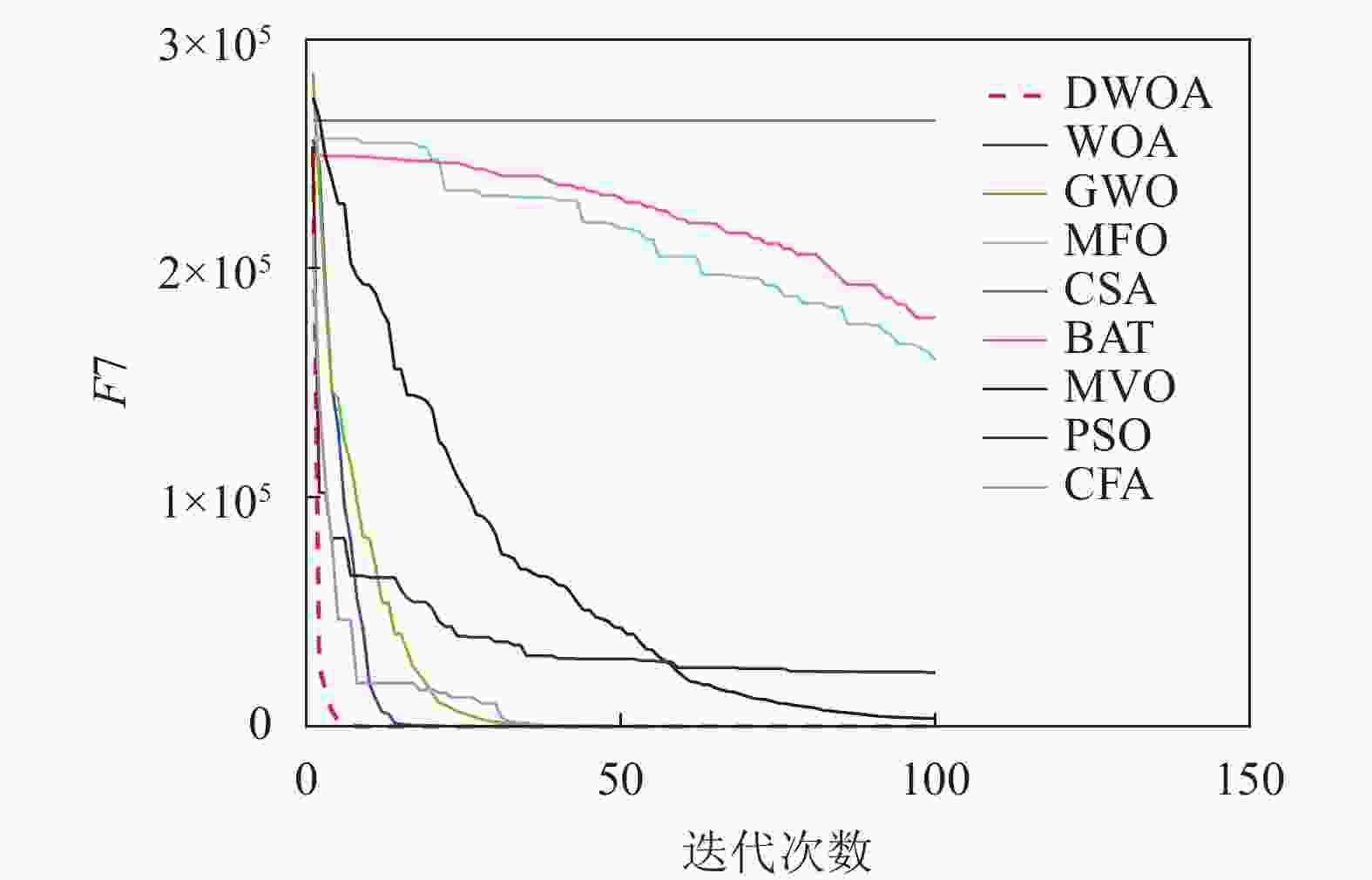
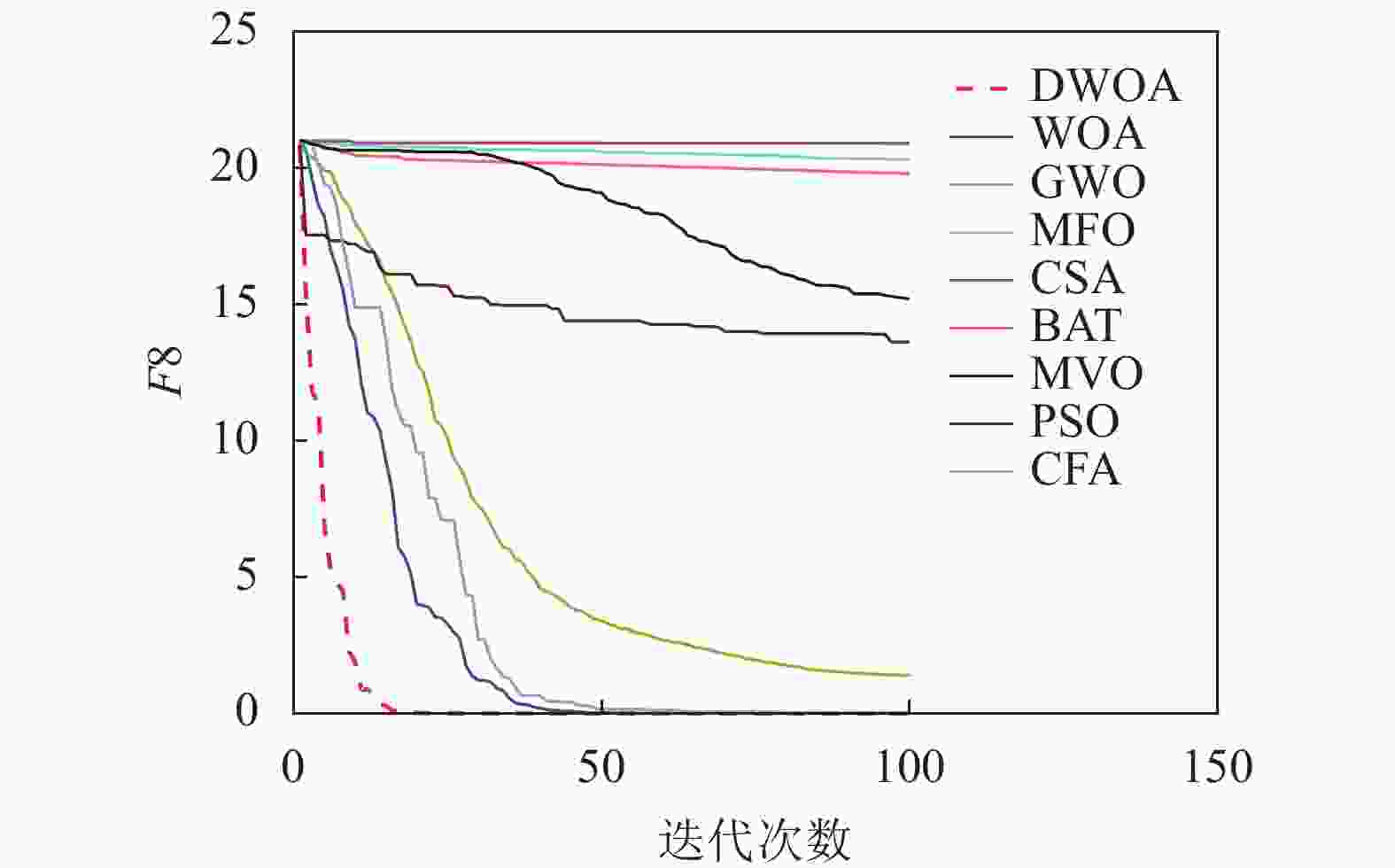
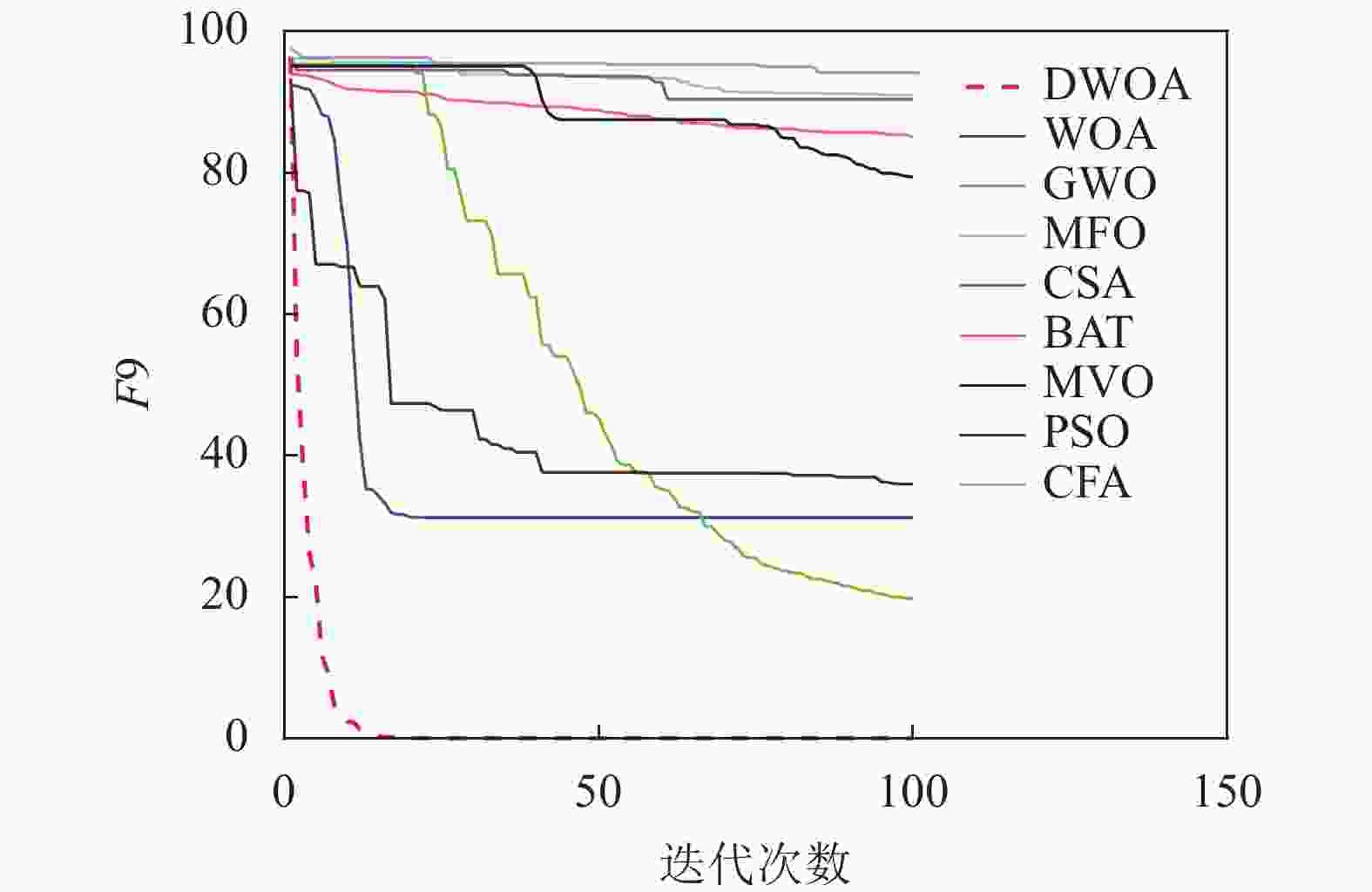
本文将离散鲸鱼算法(DWOA)同标准鲸鱼算法(WOA)[1]、灰狼算法(GWO)[13]、飞蛾扑火算法(MFO)[14]、布谷鸟算法(CSA)[15]、蝙蝠算法(BAT)[16]、多元宇宙算法(MVO)[17]、粒子群算法(PSO)[18]、乌贼算法(CFA)[19]8种优化算法进行实验对比,参数设置如表1所示,选用了9个(F1~F9)常用的基准测试函数[12]如表2所示。对于每种测试函数,算法的参数设置如下:最大迭代次数为100,种群数为40,重复计算10次,采用平均值(Mean),标准差值(Std)以及迭代中的最优值(Best)来评价算法的性能。F1~F9的迭代图分别如图3~图11所示。
算法 参数设置 DWOA ${v_{\min }} = {\rm{0,}}{v_{\max }} = {\rm{1}}{\rm{.5}},b = 1,{w_{\min }} = 0.1$ WOA 定义螺旋形状的常数$b = 1$ GWO 惯性因子$w = 0.5$, 惯性递减率$w_{\rm{damp}} = 0.99$, 加速因子: $c1 = 1,c2 = 2$ MFO 定义螺旋形状的常数$b = 1$ CSA 布谷鸟蛋发现概率${\rm{pa = 0}}{\rm{.25}}$, 步长控制量$\alpha = 1$ BAT 响度$A{\rm{ = 0}}{\rm{.5}}$, 脉冲发射率$r{\rm{ = 0}}{\rm{.5}}$, 最小频率${Q_{{\rm{min}}}}{\rm{ = 0}}$, 最大频率${Q_{{\rm{max}}}}{\rm{ = 2}}$ MVO 虫洞存在率最大值${\rm{WE}}{{\rm{P}}_{{\rm{max}}}}{\rm{ = 1}}$和最小值${\rm{WE}}{{\rm{P}}_{{\rm{min}}}}{\rm{ = 0}}{\rm{.2}}$, 开发准确率$p{\rm{ = 0}}{\rm{.6}}$ PSO 惯性因子$w = 0.5$, 惯性递减率$w_{\rm{damp}} = 0.99$, 加速因子:$c1 = 1,c2 = 2$ CFA 伸展度常数: $r{\rm{1 = 2,}}r{\rm{2 = }} - {\rm{1}}$, 可见度常数: $v{\rm{1 = }} - {\rm{1}}{\rm{.5, }}v{\rm{2 = 1}}{\rm{.5}}$ 名称 测试函数 公式 初始范围 维数 最优值 F1 Sphere $\min \displaystyle\sum\limits_{i = 1}^D {x_i^2} $ [−100,100] 100 0 F2 Penalized $\min 0.1\left\{ {\left. {{{\sin }^2}(3{{\text π}}{x_1}) + \displaystyle\sum\limits_{i = 1}^{D - 1} \begin{array}{l} {({x_i} - 1)^2}[1 + {\sin ^2}(3{{\text π}}{x_{i + 1}})] + \\ {({x_D} - 1)^2}[1 + {\sin ^2}(2{{\text π}}{x_D})] \\ \end{array} } \right\}} \right.{\rm{ + }}\displaystyle\sum\limits_{i = 1}^D {u({x_i},5,100,4)} $ [−50,50] 100 0 F3 Quartic $\min \displaystyle\sum\limits_{i = 1}^D {ix_i^4 + {\rm{random}}[0,1)} $ [−1.28,1.28] 100 0 F4 Rosenbrock $\min \displaystyle\sum\limits_{i = 1}^D {[100{{(x_i^2 - {x_{i + 1}})}^2} + {{({x_i} - 1)}^2}]} $ [−30,30] 100 0 F5 Rastrigrin $\min \displaystyle\sum\limits_{i = 1}^D {[x_i^2 - 10\cos (2{{\text π}}{x_i}) + 10]} $ [−5.12,5.12] 100 0 F6 Griewank $\min \displaystyle\sum\limits_{i = 1}^D {\dfrac{{x_i^2}}{{4\;000}}} - \prod\limits_{i = 1}^D {\cos \left( {\dfrac{{{x_i}}}{{\sqrt i }}} \right)} + 1$ [−600,600] 100 0 F7 Step $\min \displaystyle\sum\limits_{i = 1}^D {{{(\left| {{x_i} + 0.5} \right|)}^2}} $ [−100,100] 100 0 F8 Ackley $\min - 20\exp \left( { - 0.2\sqrt {\dfrac{1}{D}\displaystyle\sum\limits_{i = 1}^D {x_i^2} } } \right) - \exp \left( {\dfrac{1}{D}\displaystyle\sum\limits_{i = 1}^D {\cos (2{{\text π}}{x_i})} } \right) + 20 + \exp (1)$ [−32,32] 100 0 F9 Schwefel 2.21 $\min \{ \left| {\left. {{x_i}} \right|,1 \leqslant i} \right. \leqslant D\} $ [−10,10] 100 0 表3为9种算法在9个测试函数中的实验结果对比,从表3可以看出,在函数条件设定相同的情况下,DWOA算法能够找到F5和F6的理论最优值,对于F1、F3、F8、F9函数来说,虽然DWOA精度没有达到理论最优,但算法的搜索结果无限接近理论最优值,与其他8个算法的实验结果相比,在寻优精度上有了很大的提高,也更加稳定。
以最优值和平均值为评判标准,通过比较9种算法的优化结果可知,在每个测试函数都是100维的条件下,DWOA寻优结果最好,分析其原因在于:在进化中引入自适应惯性权值可以更好地平衡算法的全局搜索和局部开发能力,克服了算法在求解某些高维复杂函数问题时收敛速度慢,容易陷入局部最优的缺点,从F1~F9的运行结果可以看出,DWOA的算法的收敛速度更快。
以方差为评判标准,DWOA的收敛精度和方差都优于其他8种算法,分析主要原因是:在迭代过程中其他改进算法的个体会逐渐集中在最优个体的位置附近,无法跳出局部最优,而本文收敛因子可以调节个体距离最优位置的远近程度,增加了算法局部搜索的精度,有利于进行局部精细挖掘。从F1~F9的运行结果可以看出,DWOA算法寻优结果更好,证明其跳出局部最优能力得到了提升。
名称 指标 DWOA WOA GWO MFO CSA BAT MVO PSO CFA F1 Mean 3.20×103 1.18×104 2.17×104 2.16×105 2.74×105 2.15×105 7.18×104 3.63×104 6.06×104 Std 2.65×104 4.70×104 5.37×104 2.54×104 3.63×103 2.51×104 7.26×104 2.70×104 1.10×105 Best 1.58×10−31 1.95×10−15 20.854 37 1.75×105 2.71×105 1.57×105 5.11×103 1.83×104 1.01×10−7 F2 Mean 4.79×107 2.03×108 3.51×108 2.89×109 4.66×109 2.75×109 1.09×109 1.36×108 4.78×109 Std 4.63×108 8.40×108 1.05×109 5.40×108 6.71×10−6 1.32×109 1.53×109 5.71×108 1.44×108 Best 5.000 743 5.019 411 41.888 09 2.00×109 4.66×109 6.32×108 4.45×106 1.14×107 4.63×109 F3 Mean 17.392 93 1.01×102 94.97935 1.31×103 1.66×103 5.43×102 3.03×102 1.09×102 1.14×103 Std 1.69×102 3.61×102 2.83×102 3.36×102 64.008 79 1.84×102 4.73×102 2.17×102 7.80×102 Best 0.001618 0.002 505 0.065 976 7.24×102 1.62×103 3.52×102 3.926 793 25.844 82 2.983 437 F4 Mean 1.07×107 4.78×107 7.72×107 8.98×108 1.08×109 5.82×108 2.11×108 4.24×107 1.05×109 Std 1.04×108 1.97×108 2.03×108 1.68×108 4.39×107 3.99×108 3.01×108 1.2×108 5.26×107 Best 98.215 81 98.224 25 1.16×103 5.79×108 1.01×109 6.86×107 2.11×106 8.28×106 1.02×109 F5 Mean 47.658 84 1.60×102 6.72×102 1.27×103 1.55×103 1.11×103 1.25×103 9.68×102 2.24×102 Std 2.15×102 4.05×102 3.61×102 1.53×102 30.454 32 1.49×102 1.35×102 1.14×102 2.73×102 Best 0 1.14×10−13 2.30×102 1.05×103 1.52×103 9.12×102 9.16×102 8.93×102 75.222×108 F6 Mean 30.05138 1.00×102 1.83×102 2.07×103 2.46×103 2.16×103 6.13×102 4.22×102 1.43×102 Std 2.44×102 3.97×102 4.54×102 2.48×102 37.983 83 40.477 91 6.38×102 2.44×102 4.79×102 Best 0 9.99×10−16 1.069 829 1.60×103 2.43×103 2.07×103 50.082 25 2.60×102 0.288 459 F7 Mean 3.48×103 1.25×104 2.03×104 2.28×105 2.64×105 2.53×105 6.97×104 3.99×104 2.65×104 Std 2.83×104 4.45×104 5.03×104 3.03×104 2.93×10−10 2.63×104 7.11×104 3.07×104 7.47×104 Best 5.14572 5.960 822 30.370 96 1.64×105 2.64×105 1.95×105 4.56×103 2.15×104 23.795 77 F8 Mean 0.757 705 3.507 511 6.014 612 20.639 71 20.810 35 20.290 52 20.381 43 15.839 76 20.360 69 Std 3.010 918 6.414 977 6.438 818 0.169 238 2.86×10−14 0.260 663 0.166 892 1.010 50 0.185 286 Best 4.44×10−15 4.87×10−8 0.865 164 20.324 10 20.810 35 19.945 66 20.145 31 14.566 14 20.219 25 F9 Mean 2.742 325 37.247 32 53.052 34 93.361 84 92.654 89 88.703 08 89.242 66 44.175 33 95.352 73 Std 12.043 100 16.869 06 28.906 30 1.776 699 1.891 686 2.489 666 5.257 728 12.001 02 0.728 189 Best 4.58×10−9 31.222 24 19.763 52 90.948 71 90.402 55 85.064 51 79.386 84 35.983 38 94.125 31 综上所述,改进的策略提高了DWOA算法寻优性能,其优化性能比其他算法更加有效,能够有效解决高维复杂数值优化问题。
-
本文利用DWOA优化油田措施规划模型,以年度利润投入比和累积利润投入比最大为目标函数,建立油田措施规划模型,通过和其他8种算法优化结果进行对比,分析DWOA在优化油田措施规划中的性能。
-
1) 目标函数
油田措施规划问题是在满足油田开采要求的各种约束条件的前提下,合理分配开采井组,使油田的年度利润投入比和累积利润投入比最大,其目标函数为:
式中,
${F_1}$ 是年度利润投入比;${F_{\rm{2}}}$ 是累积利润投入比;$N$ 为井数目;$K$ 为措施数;a、b、c分别是吨油成本、吨水成本、吨液成本;$x{{\rm{1}}_{ij}}$ 为第$i$ 口油井第$j$ 个措施的年度增油量;$y{{\rm{1}}_{ij}}$ 为第$i$ 口水井第$j$ 个措施的年度增油量;$z{{\rm{1}}_{ij}}$ 为第$i$ 口井第$j$ 个措施的年度增液量;$w{{\rm{1}}_{ij}}$ 为第$i$ 口井第$j$ 个措施的年度增注量;$x{{\rm{2}}_{ij}}$ 为第$i$ 口油井第$j$ 个措施的累积增油量;$y{{\rm{2}}_{ij}}$ 为第$i$ 口水井第$j$ 个措施的累积增油量;$z{{\rm{2}}_{ij}}$ 为第$i$ 口井第$j$ 个措施的累积增液量;$w{{\rm{2}}_{ij}}$ 为第$i$ 口井第$j$ 个措施的累积增注量;${\rm{pric}}{{\rm{e}}_{ij}}$ 是第$i$ 口井措施数为$j$ 的价格。2) 约束条件
① 增油量约束为:
式中,
${t_{\rm{o}}}$ 是油井增油目标;${t_{\rm{e}}}$ 是水井增油目标;$\partial {\rm{ = 0}}{\rm{.03}}$ 为误差百分比。② 增液量和增注量约束为:
式中,
${t_{\rm{l}}}$ 是增液量上限;${t_{\rm{c}}}$ 是增注量上限。③ 措施数上限约束为:
式中,
${\rm{Limi}}{{\rm{t}}_{ij}}$ 是采油井的措施数上限。 -
结合采油厂某区块当年的生产任务,采取的措施和工作目标包括:油井压裂为61口、油井补孔为161口、油井堵水为47口、油井换泵为109口、水井压裂为50口、水井酸化为705口、水井补孔为36口、水井测调为404口、水井细分为293口、水井周期为151口、水井浅调为434口、水井深调为39口,共计2 490口措施井。其中,油井增油目标为
${\rm{7}}{\rm{.1}} \times {\rm{1}}{{\rm{0}}^4}$ T,水井增油目标为${\rm{7}}{\rm{.5}} \times {\rm{1}}{{\rm{0}}^4}$ T,年增液量上限为${\rm{18}} \times {\rm{1}}{{\rm{0}}^4}$ T,年增注量上限为${\rm{30}} \times {\rm{1}}{{\rm{0}}^4}$ m3,误差百分比$\partial $ 为0.03。算法 年度利润投入比(F1) 最优值 最差值 平均值 方差 DWOA 3.264 96 2.908 77 3.154 61 0.133 31 WOA 3.068 76 2.789 15 3.021 25 0.090 70 GWO 3.048 40 2.793 57 3.014 22 0.069 26 MFO 2.845 29 2.793 66 2.838 76 0.012 63 CSA 2.963 69 2.774 62 2.925 23 0.057 86 BAT 3.029 23 2.774 62 2.994 19 0.072 93 PSO 3.206 33 2.791 10 3.058 15 0.178 57 MVO 2.923 92 2.863 85 2.922 72 0.008 41 CFA 3.236 10 2.754 66 3.097 33 0.133 67 算法 累积利润投入比(F2) 最优值 最差值 平均值 方差 DWOA 3.285 33 3.027 14 3.148 20 0.121 66 WOA 3.243 67 2.961 45 3.200 67 0.085 82 GWO 3.205 08 2.880 92 3.176 78 0.068 54 MFO 3.108 96 2.851 16 3.080 36 0.052 42 CSA 3.220 77 2.934 19 3.198 03 0.055 72 BAT 3.272 53 2.934 19 3.229 06 0.093 87 PSO 3.250 27 2.810 88 3.140 66 0.134 88 MVO 3.164 60 3.011 13 3.161 53 0.021 48 CFA 3.184 46 2.865 56 3.085 87 0.086 24 为验证本文算法求解油田措施规划模型的高效性,采用9种优化算法针对2 490口措施井进行油水井措施方案优选,并将实验结果进行对比分析。算法的参数设置如表3所示,种群大小为100,最大迭代次数为1 000,每20代取一次平均值作为最优值。
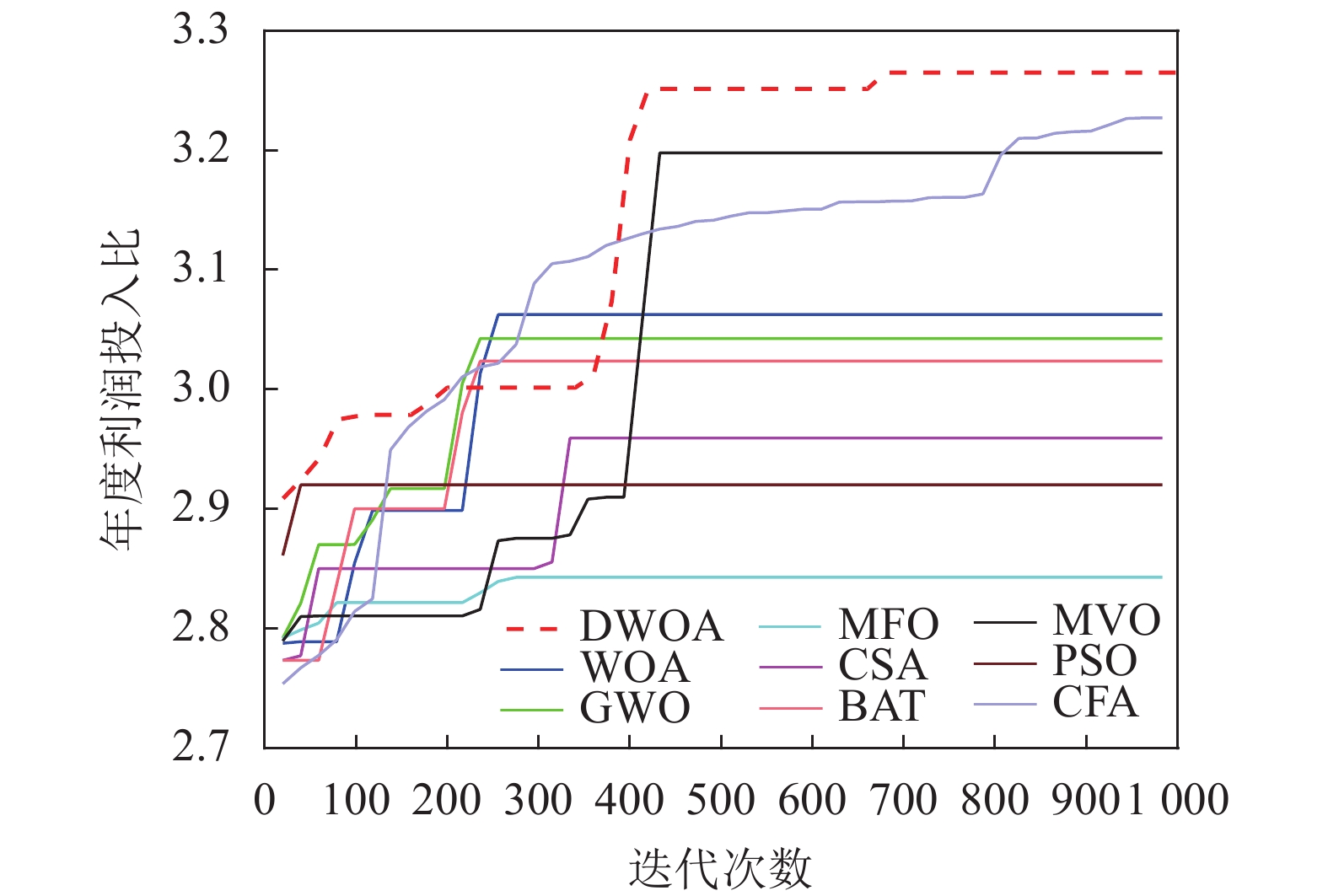
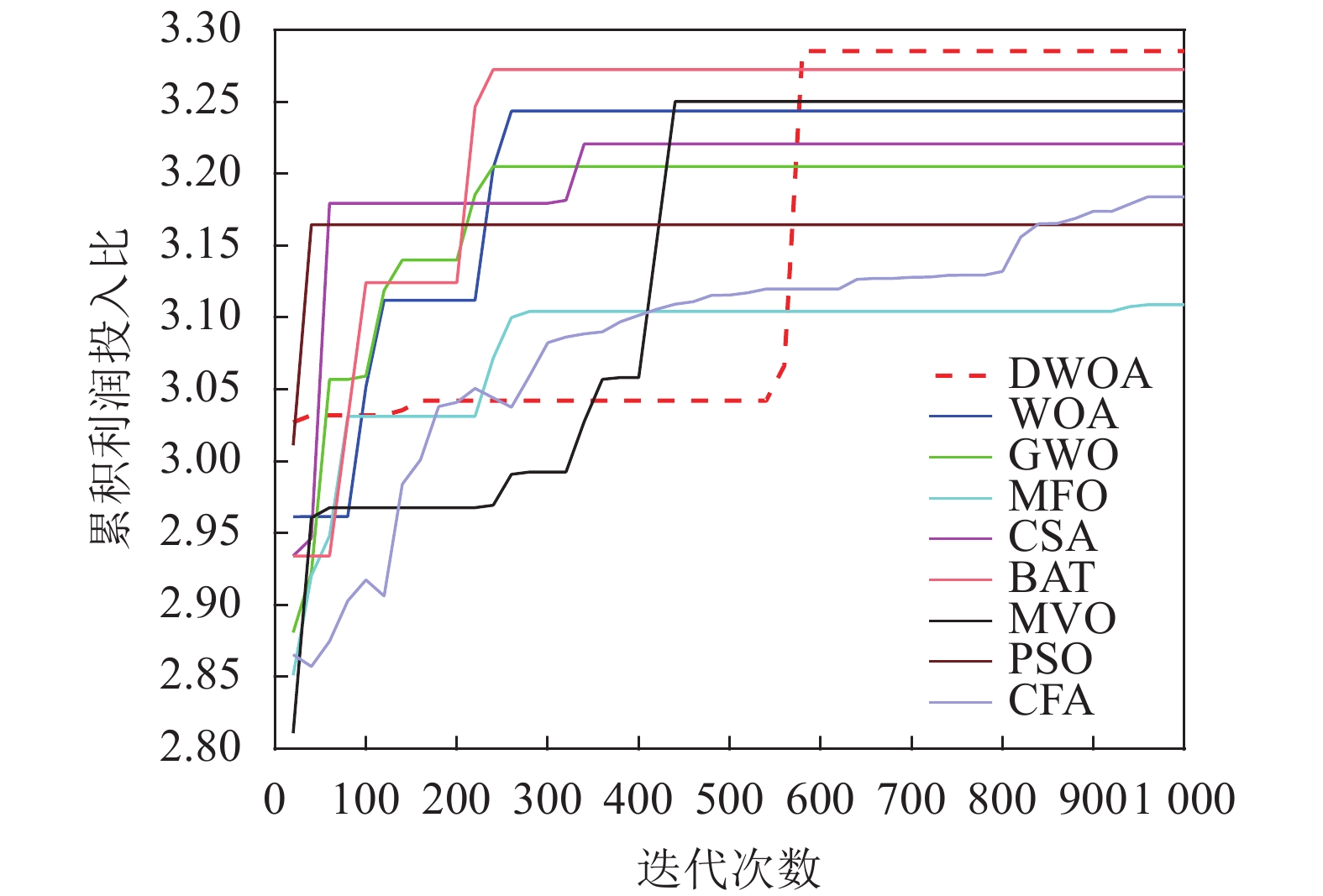
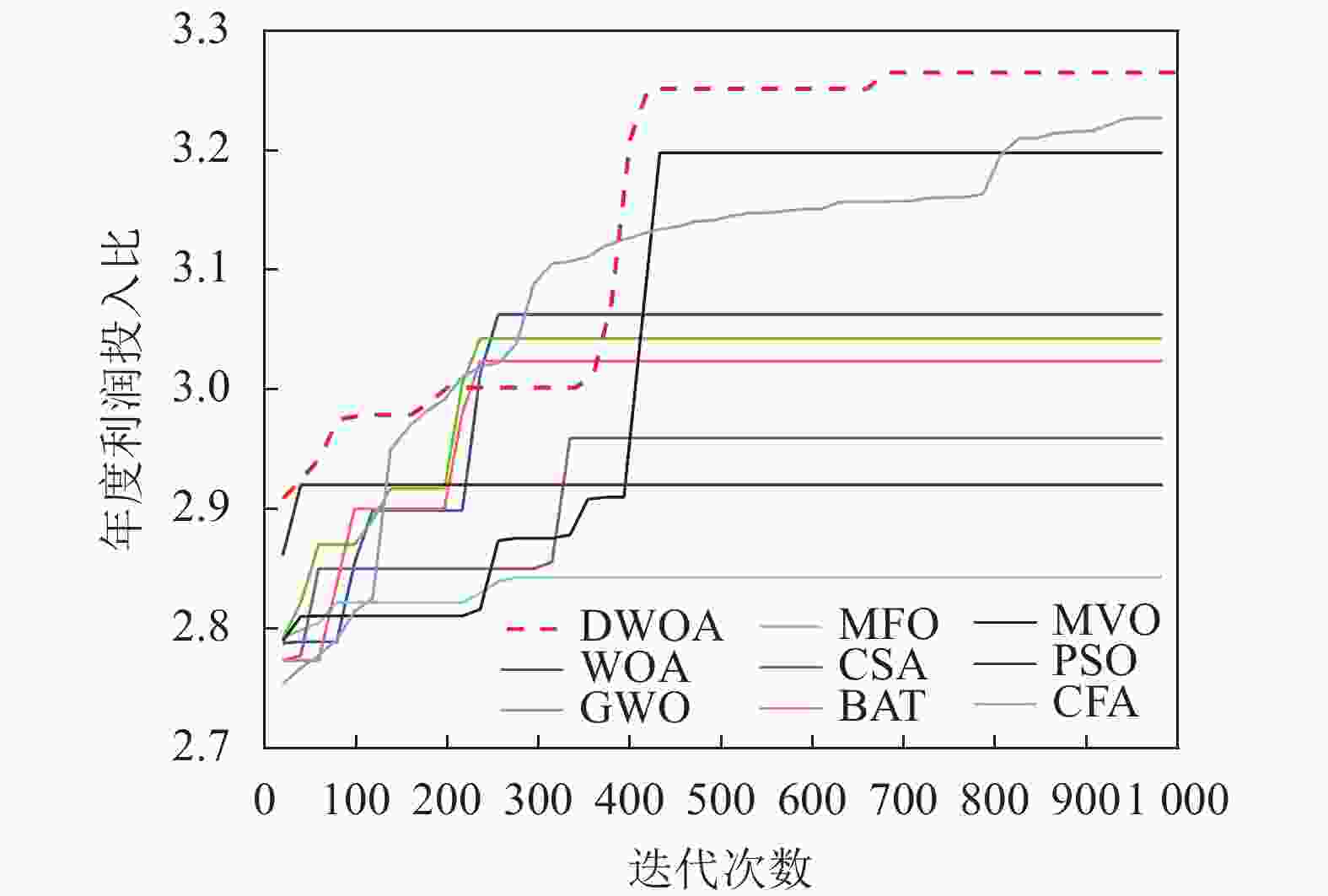
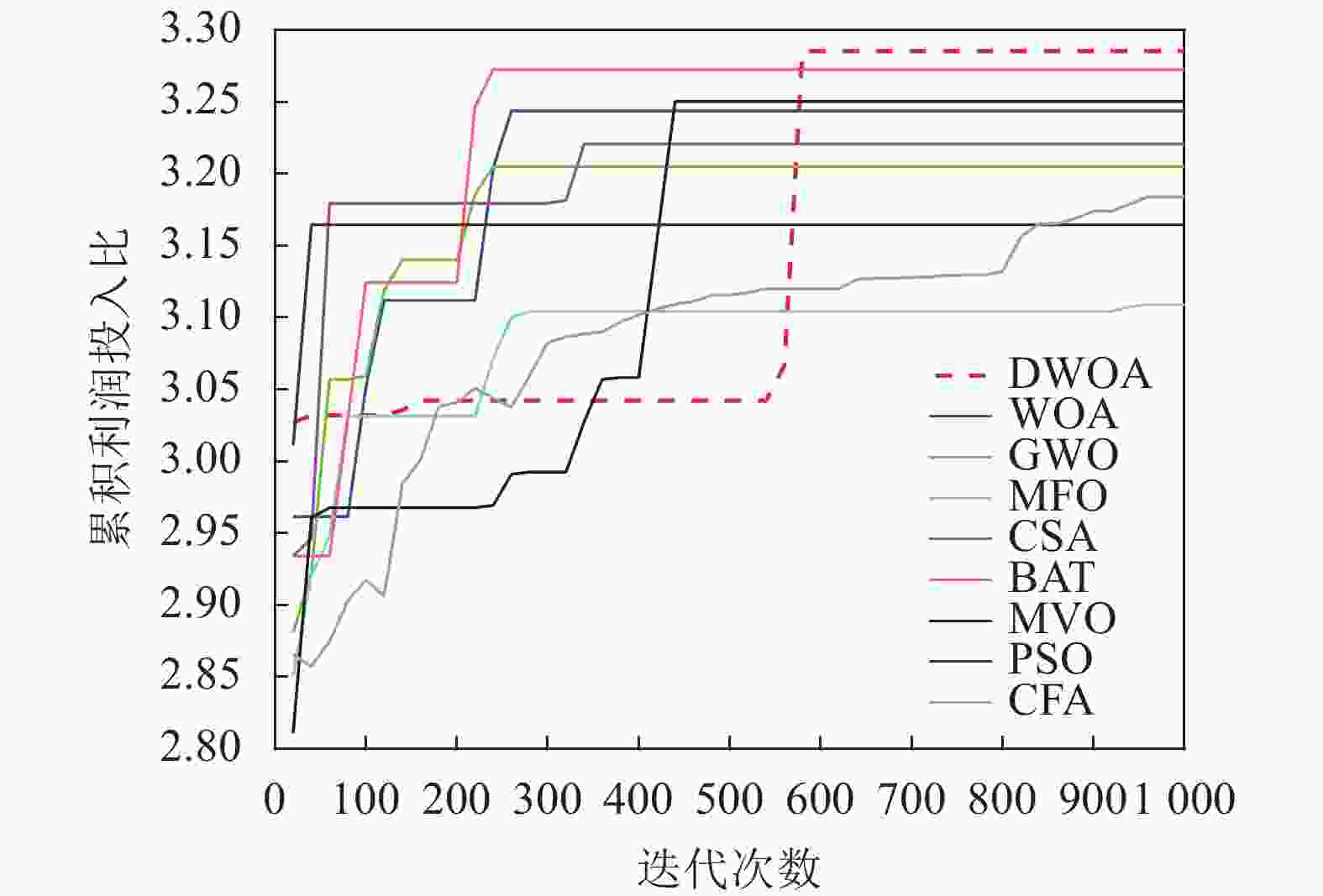
本文实验解决的主要问题是使年度利润投入比和累积利润投入比最大化,表4、表5总结了9种算法优化得到的最优值、最差值、平均值、方差,图12、图13表示的是9种优化算法运行时的结果相对于迭代次数的变化情况。
由表4和表5分析可知,从最优值、最差值方面来看,在求解油田措施模型问题中,DWOA得到的优化结果最好。在迭代过程中,DWOA算法引入了收敛因子,可以更好地调控最优个体和其他个体之间的距离,精细算法的局部搜索能力,有更大的潜力去寻找潜在的优秀解;此外,随着迭代的进行,自适应权值逐渐减小,可以平衡迭代后期算法的全局搜索和局部开发能力,提高算法的收敛速度;在对位置更新方式进行离散化处理时,应用改进的Sigmoid函数离散化位置向量,可以更好地对0−1编码方式进行概率映射,保证了经过离散化处理后,粒子的多样性不会骤减,避免了算法过早陷入局部最优解,可以充分挖掘搜索空间。
从方差和平均值方面可以看出,DWOA算法相较于其他算法有较好的稳定性。从图12和图13中可知,PSO算法最早陷入局部最优,过早收敛严重影响了PSO算法的性能,BAT、GWO、MFO、WOA算法在250代左右最优值不再发生变化,而MVO算法在450代以后也陷入局部最优,但由于收敛因子提高了DWOA算法跳出局部最优的能力,因此DWOA算法的收敛曲线在600代时仍有上升的趋势,能够寻找到更优的解。
综上所述,从实际应用结果验证来看,DWOA算法在求解油田措施规划模型时,有着良好的开发和勘探能力,可以得到较优的结果,提高油田开采的经济效益。
-
鲸鱼优化算法是模拟座头鲸狩猎机制而提出的一种新的群智能优化算法,本文提出一种离散鲸鱼算法(DWOA),利用收敛因子来控制个体到最佳解位置的距离,提高算法的局部搜索能力;引入自适应惯性权值来提高算法的全局搜索能力,提高了DWOA算法的收敛精度和收敛速度;并用改进的Sigmoid函数离散化位置更新方式,保证种群进化过程中的多样性。基准测试函数实验验证了改进策略的有效性和可行性,并成功地将其应用到油田措施规划模型优化问题中。结果表明,同其他8种优化算法相比,DWOA算法求解质量取得了很好的效果。今后的研究工作一方面会通过更多的实验来验证并改进算法的性能,另一方面将探索本文算法在其他工程应用领域的可行性,以扩大算法的应用范围。
A Discrete Whale Optimization Algorithm and Application
doi: 10.12178/1001-0548.2019116
- Received Date: 2019-05-10
- Rev Recd Date: 2020-05-25
- Available Online: 2020-07-29
- Publish Date: 2020-07-10
-
Key words:
- adaptive inertia weight /
- convergence factor /
- discrete whale optimization algorithm (DWOA) /
- oilfield measures planning /
- Sigmoid
Abstract: A discrete whale optimization algorithm (DWOA) is proposed to overcome the defects of low convergence and the lack of ability to solve discrete optimization problems when solving high-dimensional complex problems. In DWOA, the convergence factor is introduced to adjust the distance of the individual from the optimal whale position, the adaptive inertia weight is designed to balance the global exploration and local exploitation ability, the whale optimization algorithm (WOA) is discretized by the improved Sigmoid function. The optimization experiments are conducted on the 9 benchmark functions and oilfield measures planning. Simulation results show that the proposed DWOA has a great improvement in convergence speed and convergence precision.
| Citation: | ZHANG Qiang, GUO Yu-jie, WANG Ying, LIU Xin. A Discrete Whale Optimization Algorithm and Application[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(4): 622-630. doi: 10.12178/1001-0548.2019116 |

 ISSN
ISSN 
















































































































 DownLoad:
DownLoad: