Fitness of the Generalized Growth to the COVID-19 Data

理论上，在病毒传播的初期，因资源不受限制，其增长方式呈指数函数，满足：

式中，$y(t) = y(0){{\rm{e}}^{rt}}$，$y(0)$为初始感染人数，$r$为增长速率。然而，在很多已经爆发的传染病中，相比于指数增长，次指数的增长趋势在疫情传播初期更为常见。如HIV/AIDS^[2-4]、埃博拉^[5]和手足口^[6]等实证数据，都呈现了次指数的增长方式。

次指数增长方式的内在机制，主要有如下几方面解释：空间异质性、群聚感染^[6-7]、以及感染参数的时间异质性^[4]等。在SIR模型中，考虑空间异质性^{[4, 7-9]}、传染率的时变性^{[6-7, 9-12]}以及异质混合模型^[13-14]，都能够呈现出次指数的增长方式。考虑到2020年1月23日武汉开始“封城”，加之全国各省市防疫工作的陆续开展，新冠肺炎传播在时间、空间上异质性明显，且发病多呈现集聚感染的情况，都与次指数增长方式产生的机制吻合。

下文的拟合中，在次指数模型的基础上，拓展模型参数范围，使其不仅适用于疫情发展初期的指数增长和次指数增长，还适用于疫情发展到当前阶段，增长速度放慢情形的拟合，拟合结果与国家卫生健康委员会每日发布的累计确诊人数、累计疑似人数和累计密切接触人数的公布数据高度契合。

本文在文献[2, 7]给出的病毒传播的一般增长(generalized-growth)模型基础上，对尺度参数进行扩展。首先，一般增长模型在式(1)的指数增长微分方程基础上，引入可调参数$p \in [0,1]$，称为增长率的负加速度参数。一般增长模型刻画的累计感染人数$y(t)$满足：

式中，$r > 0$表示增长率；$p \in [0,1]$为增长率的负加速度参数，当$p = 0$时，累计感染人数呈线性增长；当$p = 1$时，方程退化为式(1)。

微分方程(2)的精确解为：

式中，$y(0)$为初值；当$0 < p < 1$时，$y(t)$呈次指数增长模式，且$p$越接近于1，$y(t)$越接近指数增长；参数$p$的范围扩展为$p \leqslant 1$，当$p < 0$时，$y(t)$将呈次线性增长。下文对累计确诊人数、累计疑似人数及累计密切接触人数的拟合方程均为式(3)。

新冠肺炎疫情的发展经历了不同的增长模式。本文将确诊数据的拟合分为三个阶段：无障碍指数增长、次指数增长及次线性增长阶段，反映了疫情防控工作的阶段进展，为新冠肺炎疫情的趋势预测提供参考。

本文数据采集自国家卫生健康委员会每日疫情通报。数据采用每天更新的前一天0～24时全国病例更新数据，采集数据包括全国确诊累计病例数、全国疑似累计病例数和全国密切接触累计人数，数据截至2020年2月15日24时。

以式(3)对2020年1月15日−2月15日全国新冠肺炎的累计确诊人数、2020年1月23日−2月15日的累计疑似人数和累计密切接触人数，进行非线性拟合，拟合参数包括$r$、$p$和$y(0)$。

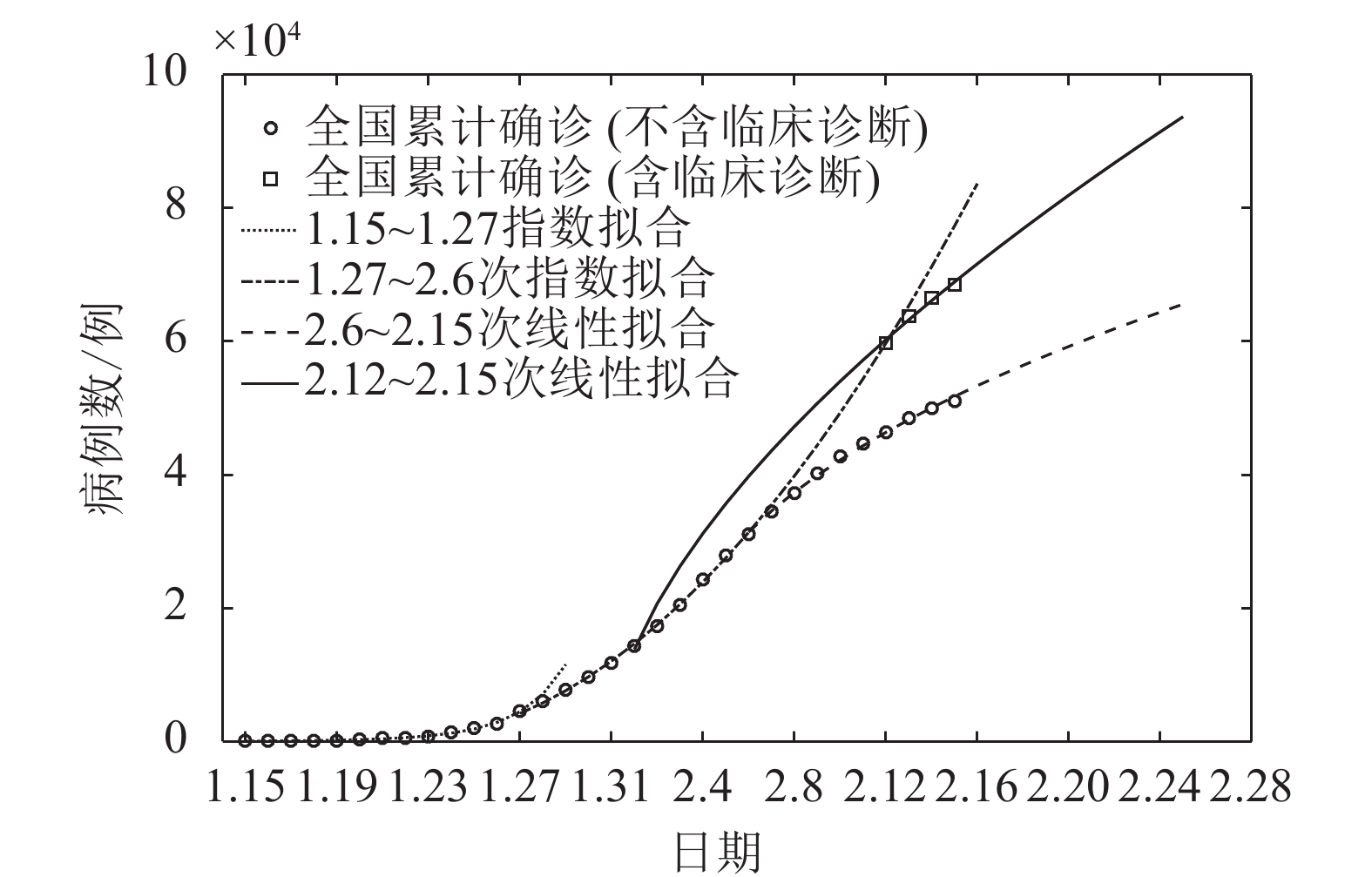
参考疫情发展的关键时间节点，全国新冠肺炎累计确诊病例数的拟合分三个阶段，第一阶段为2020年1月15日−1月27日，本阶段的疫情确诊人数拟合参数为：

从拟合参数看，$p$约为1，这一阶段新冠肺炎确诊人数呈指数增长，其原因是疫情发展初期，病毒广泛传播。

第二阶段为2020年1月27日−2月6日。本阶段拟合参数为：

此阶段尺度参数$p < 1$，增长呈现次指数的幂函数增长。经过上一阶段疫情的迅猛发展，人们防护意识增强，减少出行，主动隔离，疫情传播得到一定程度的抑制，同时诊断能力有限。

第三阶段为2020年2月6日至本文数据截止时间2020年2月15日。除去临床确诊病例数，本阶段的拟合参数为：

这一阶段，$p < 0$，式(3)的增速小于线性。“封城”14日后，第一个隔离期结束，火神山医院启用，全国各地医护人员驰援疫情发源地，疫情得到有效控制。在这一阶段，控制成效显著。

2020年2月12日−2月15日发布了含临床诊断的确诊病例数。采用这4日的数据，得到如下拟合参数：

尽管4天的数据量少，仍能为疫情发展趋势提供参考。实证数据与拟合曲线如图1所示。

在图1中，2020年1月27日−2月6日的次指数拟合曲线(图中点划线)，其预测值与2月12日公布的含临床确诊病例数据非常接近；2月12日−2月15日含临床诊断的确诊病例数据的次线性拟合曲线(图中实线)向前追溯11日，与2月1日公布的确诊病例数据接近。尽管这两条曲线无法得知2月12日之前含临床诊断的确诊数据的演化方式，仍能为认识该阶段疫情发展提供参考。

2020年2月12日−2月15日含临床诊断的累计确诊病例数呈次线性增长，拟合参数为$p = - 0.659$。结合下文累计疑似病例数与累计密切接触人数的增长趋势，次线性增长方式将在一定时间段内持续，其次线性的参数$p$将进一步减小，增速会放缓。疫情目前处于胶着对峙阶段。

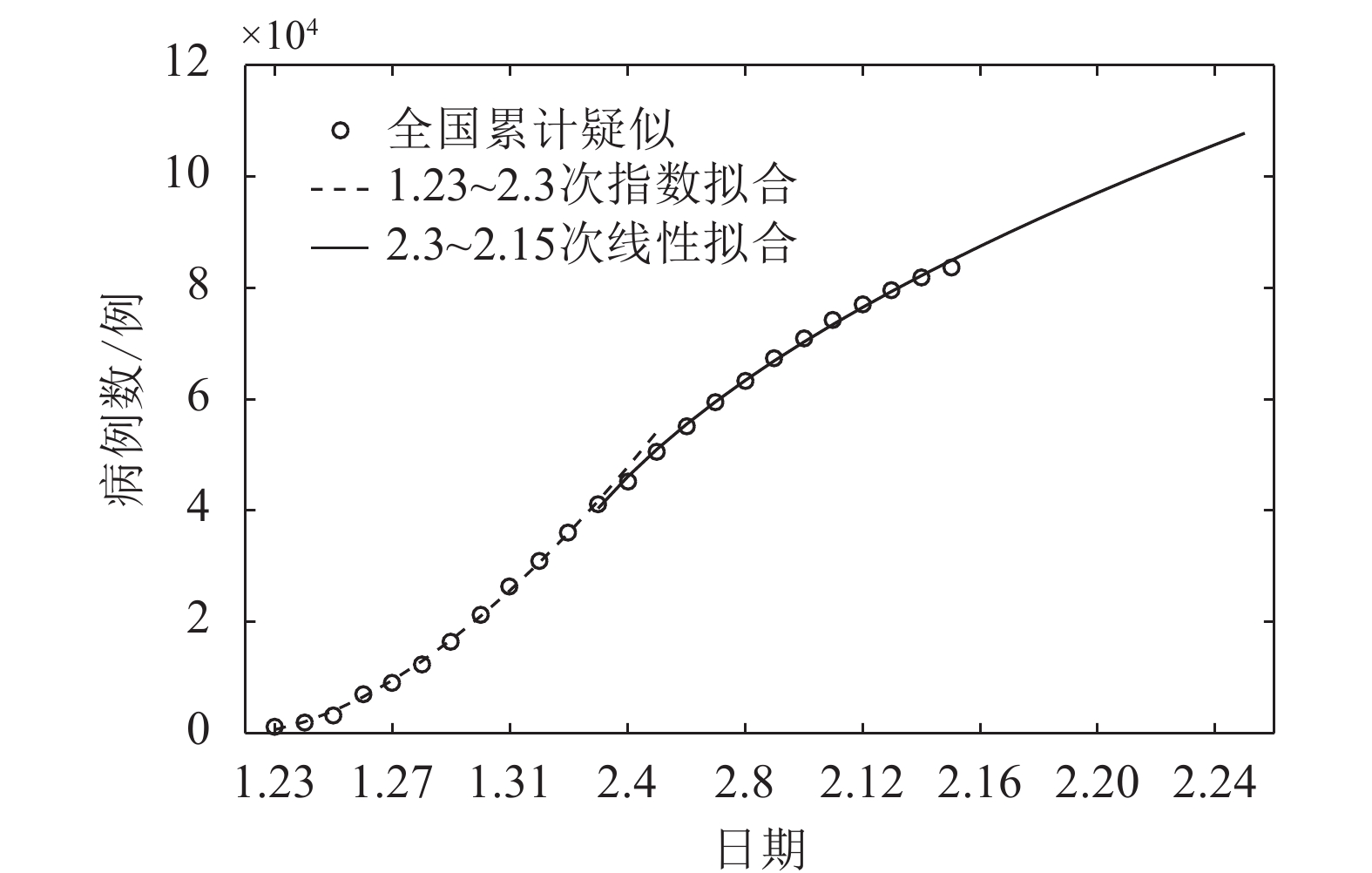
新冠肺炎累计疑似病例数拟合的分为两个阶段。第一阶段为2020年1月23日−2月3日，拟合参数为：

这一阶段为次指数增长，$p = 0.409$。武汉“封城”后，人们对防控疫情的重视程度提升，疫情得到了一定程度的控制，疫情发展呈现次指数。

第二阶段为2020年2月3日至本文数据截止时间2月15日。拟合参数为：

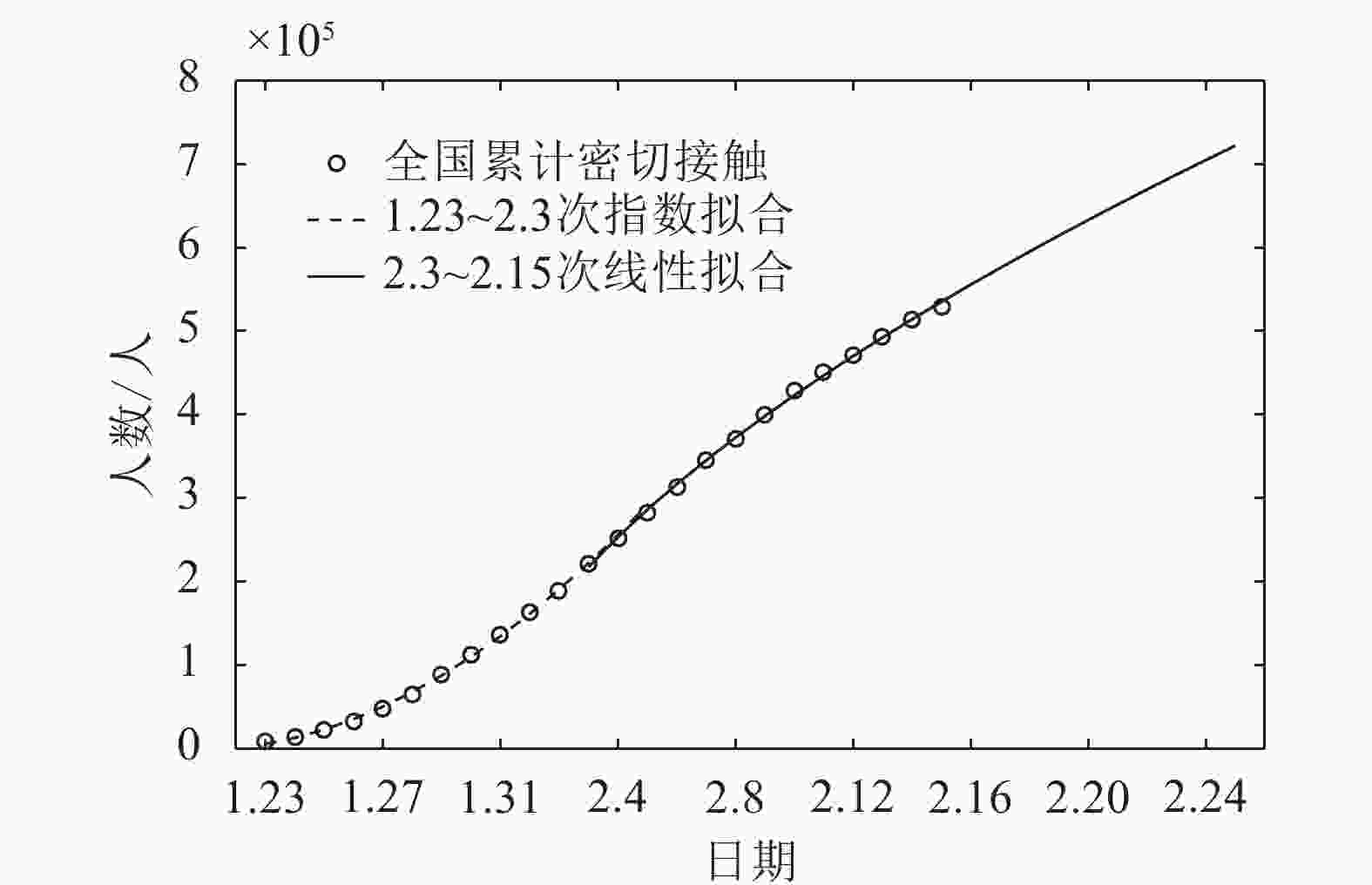
疑似人数随着医疗资源的配置得到快速诊断，疑似人数次线性指数$p = - 1.126$，累计疑似人数增长呈次线性，且次线性程度较大。实证数据与拟合曲线如图2所示。

新冠肺炎疫情累计密切接触人数的拟合与疑似人数类似。同样分为两个阶段，第一阶段为2020年1月23日−2月3日，拟合参数为：

第二阶段为2020年2月3日−2月15日，拟合参数为：

从两阶段的参数看，疑似与接触在次指数增长阶段的参数较为相似，但在次线性阶段的参数反映了累计密切接触人数的下降幅度并没有预期的快，其原因或与确诊后的追踪滞后有关。累计密切接触人数的实证数据与拟合曲线如图3所示。

本文借助一般增长模型，对新冠肺炎疫情的确诊、疑似和密切接触人数进行分阶段非线性拟合。拟合结合疫情发展过程，进行合理分段，拟合结果与实证数据高度吻合，能够为疫情的防控效果以及发展趋势提供参考。

指数、次指数、次线性函数的增长方式均由式(3)给出，其背后的产生机制可从非时齐随机过程和随机环境中的随机过程的理论中得到启示。新冠疫情的发展过程可用年龄依赖的分枝过程刻画，其中年龄用来刻画每位患者从感染到确诊并隔离住院的这段时间，在此期间，新冠肺炎病毒携带者具有传染性，并能够感染给更多与之接触的人，可建模为该患者的“后代”。结合新冠肺炎疫情传播的实际情况，该年龄依赖分枝过程的年龄分布、后代分布随疫情防控的进展，均呈现非时齐的特点。文献[15]也指出，疾病传播过程可由非时齐分枝过程相对应。尽管关于非时齐年龄依赖分枝过程已有相关研究^[16-17]，但与新冠肺炎疫情发展一致的非时齐模型并未得到深入研究，这也将是接下来的研究工作，借助非时齐的年龄依赖分枝过程，从仿真和理论两方面，揭示新冠疫情传播的内在机制。

致谢 感谢北京师范大学新闻传播学院吴晔教授的交流与讨论。