-
量子密码的安全基于海森堡不确定原理[1]和量子不可克隆定理[2]。近年来,随着量子密码应用的发展,量子密码学引起越来越多的关注,研究成果层出不穷,包括量子密钥分发(quantum key distribution, QKD)[3-4]、量子密钥协商(quantum key agreement, QKA)[5]、量子秘密共享(quantum secret sharing, QSS)[6]、量子安全直接通信(quantum secure direct communication, QSDC)[7]、量子私有比较(quantum private comparison, QPC)[8]以及量子远程态准备(quantum remote state preparation, QRSP)[9]等。量子密钥协商(QKA)是量子密码学的一个重要研究方向。它允许所有参与者共同协商一个会话密钥,并且每个参与者对生成会话密钥的贡献是相同的,即会话密钥不能由任意一方完全决定。它显然不同于QKD,因为QKD是由一个参与者决定会话密钥并将其分发给其他各方。因此,QKA在生成会话密钥方面比QKD更加公平。
QKA经过了多年的研究发展,取得了大量研究成果。2004年,文献[5]提出了第一个QKA协议,其中通信方共同确定会话密钥。2010年,文献[10]提出了一种基于BB84[3]的QKA协议,利用延迟测量技术和双CNOT操作,实现了会话密钥的公平建立。2013年,文献[11]提出了利用EPR对和纠缠交换技术将参与者由两方扩展为多方的QKA协议。2017年,文献[12]提出了两种不受集体噪声影响的QKA协议,这两种协议主要利用逻辑量子态、多粒子纠缠态的测量相关特性和延迟测量技术,使得协议的性能得到提升。2020年,文献[13]提出了一种三方半量子密钥协商协议,降低了对参与者能力和设备的要求。2020年,文献[14]提出了基于最大三粒子纠缠态的受控量子密钥协商协议,与之前的两方和三方QKA协议相比较,最大的变化是引入了一个监督者来控制协议过程,以提高协议的可控性。2021年,文献[15]提出了基于类GHz态的半诚实三方互认证量子密钥协商协议,利用身份认证部分验证用户身份的真实性,确保密钥协商双方身份的正确性与可靠性,并且能防止外部攻击者冒充合法用户传递虚假信息窃取会话密钥。这与其他QKA协议相比,更符合实际应用需求。因此,设计具有互认证功能的QKA协议有重要意义。
然而已有的互认证量子密钥协商协议需要在可信或者半可信第三方的帮助下才能实现参与者之间的密钥协商,因此步骤繁琐且通信量较大。利用Bell态,本文提出了一个无需第三方参与的两方互认证QKA协议。在该协议中,两个参与方通过对身份信息粒子的制备和测量,来实现双方身份的互认证;并且利用Bell态的纠缠交换关系和编码实现密钥协商。新的QKA协议被证明是安全的且有较高的量子比特效率。
-
4个Bell态构成了四维Hilbert空间的一组正交基,即:
任意两个Bell态纠缠交换后仍然处于一对Bell态,如:
根据式(5)可知,若对粒子
$ 1,3 $ 进行Bell基测量,测量结果为$ {\left| {{\phi ^ + }} \right\rangle _{13}},{\left| {{\phi ^ - }} \right\rangle _{13}},{\left| {{\psi ^ + }} \right\rangle _{13}} $ 或$ {\left| {{\psi ^ - }} \right\rangle _{13}} $ 的概率各是$ {1 \mathord{\left/ {\vphantom {1 4}} \right. } 4} $ ,相应粒子$ {\text{2,4}} $ 的状态也是类似的情况。其他Bell态的纠缠交换情况详见表1。Bell态 Bell态 纠缠交换后的Bell态 $ {\left| {{\phi ^ + }} \right\rangle _{12}} $ $ {\left| {{\phi ^ + }} \right\rangle _{34}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{12}} $ $ {\left| {{\phi ^ - }} \right\rangle _{34}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{12}} $ $ {\left| {{\psi ^ + }} \right\rangle _{34}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{12}} $ $ {\left| {{\psi ^ - }} \right\rangle _{34}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{12}} $ $ {\left| {{\phi ^ + }} \right\rangle _{34}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{12}} $ $ {\left| {{\phi ^ - }} \right\rangle _{34}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{12}} $ $ {\left| {{\psi ^ + }} \right\rangle _{34}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{12}} $ $ {\left| {{\psi ^ - }} \right\rangle _{34}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{12}} $ $ {\left| {{\phi ^ + }} \right\rangle _{34}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{12}} $ $ {\left| {{\phi ^ - }} \right\rangle _{34}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{12}} $ $ {\left| {{\psi ^ + }} \right\rangle _{34}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{12}} $ $ {\left| {{\psi ^ - }} \right\rangle _{34}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{12}} $ $ {\left| {{\phi ^ + }} \right\rangle _{34}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{12}} $ $ {\left| {{\phi ^ - }} \right\rangle _{34}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{12}} $ $ {\left| {{\psi ^ + }} \right\rangle _{34}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\psi ^ - }} \right\rangle _{12}} $ $ {\left| {{\psi ^ - }} \right\rangle _{34}} $ $ {\left| {{\psi ^ - }} \right\rangle _{13}}{\left| {{\psi ^ - }} \right\rangle _{24}} $ $ {\left| {{\psi ^ + }} \right\rangle _{13}}{\left| {{\psi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ + }} \right\rangle _{13}}{\left| {{\phi ^ + }} \right\rangle _{24}} $ $ {\left| {{\phi ^ - }} \right\rangle _{13}}{\left| {{\phi ^ - }} \right\rangle _{24}} $ 然后,定义Bell态的一种编码规则,即将
$ \left| {{\phi ^ + }} \right\rangle $ 编码为$ {\text{00}} $ ,$ \left| {{\phi ^ - }} \right\rangle $ 编码为$ {\text{01}} $ ,$ \left| {{\psi ^ + }} \right\rangle $ 编码为$ {\text{10}} $ ,$ \left| {{\psi ^ - }} \right\rangle $ 编码为$ {\text{11}} $ 。当用$ {C_{12}},{C_{34}} $ ,$ {C_{13}},{C_{24}} $ 分别表示不同粒子Bell态的二进制编码时,根据表1可得$ {C_{12}} \oplus {C_{34}} = {C_{13}} \oplus {C_{24}} $ ,其中$ \oplus $ 表示按位异或。 -
当Alice和Bob想要协商一个会话密钥时,他们需要先相互认证对方的身份,当身份认证通过后,Alice和Bob再进行密钥协商。协议的身份认证及密钥协商的具体步骤如下。
1) Alice和Bob事先秘密共享一对身份信息序列
$ {R_A} = R_A^1R_A^2 \cdots R_A^n $ 和$ {R_B} = R_B^1R_B^2 \cdots R_B^n $ ,其中,$ {R}_{A}^{i}, {R}_{B}^{i}\in \{0,1\} $ ,并且$ i \in \{ 1,2,3, \cdots ,n\} $ 。Alice根据身份信息序列$ {R_A} $ 制备相应的粒子序列$ {r_A} = r_A^1r_A^2r_A^3 \cdots r_A^n $ ,当$ R_A^i = 0 $ 时,$ r_A^i $ 被随机制备为$ \left| 0 \right\rangle $ 态或$ \left| + \right\rangle $ 态;当$ R_A^i = 1 $ 时,$ r_A^i $ 被随机制备为$ \left| 1 \right\rangle $ 态或$ \left| - \right\rangle $ 态。同理,Bob根据身份信息序列$ {R_B} $ 制备相应的粒子序列$ {r_B} = r_B^1r_B^2r_B^3 \cdots r_B^n $ 。2) Alice从集合
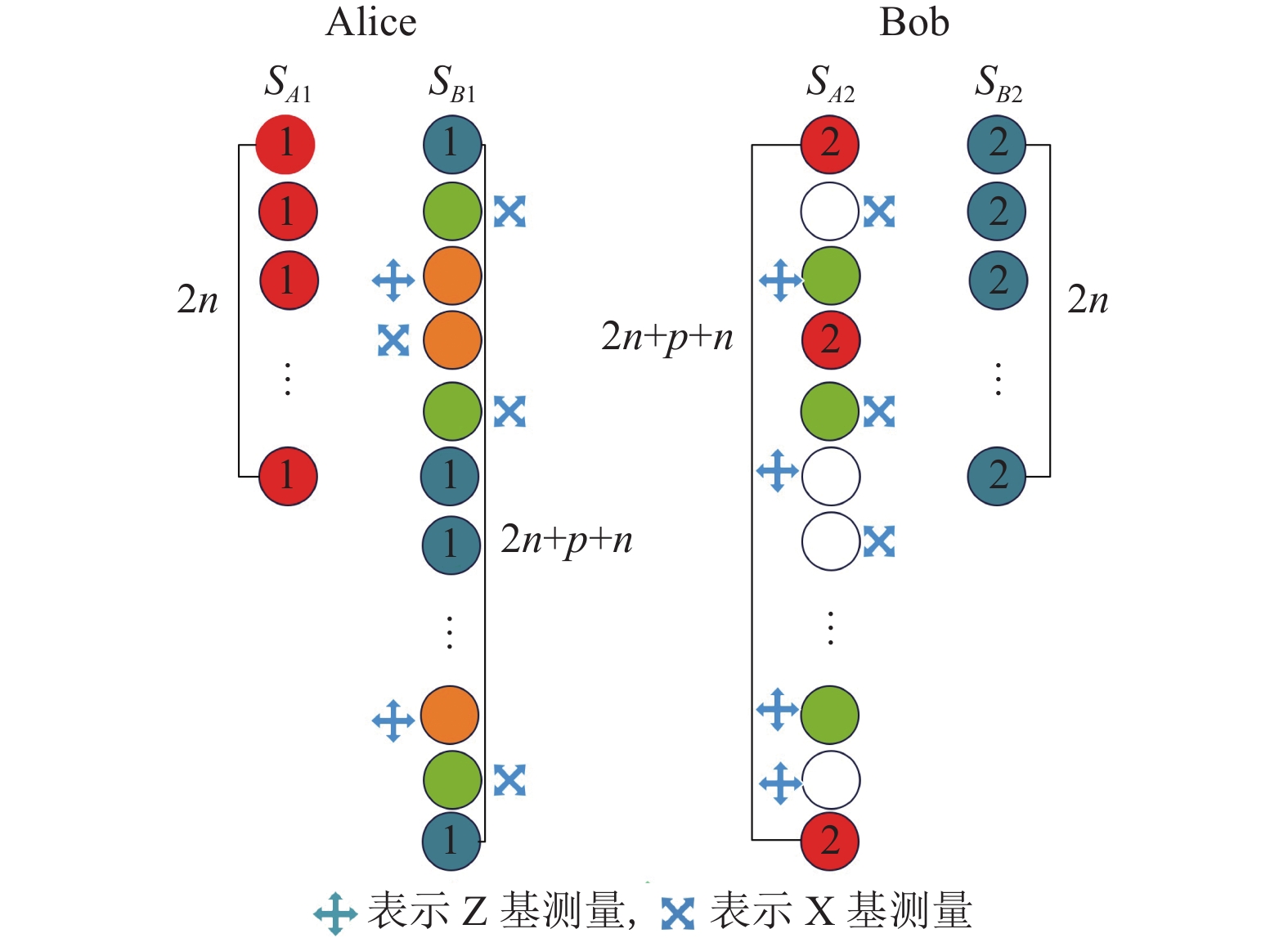
$ \left\{|{\phi }^{+}\rangle ,|{\phi }^{-}\rangle ,|{\psi }^{+}\rangle ,|{\psi }^{-}\rangle \right\} $ 中随机选择$ 2n $ 个Bell态,形成一个Bell态序列$ {S_A} = s_{{a_{12}}}^1s_{{a_{12}}}^2s_{{a_{12}}}^3 \cdots s_{{a_{12}}}^{2n} $ 。采用同样的方法,Bob也得到一个长度为$ 2n $ 的Bell态序列$ {S_B} = s_{{b_{12}}}^1s_{{b_{12}}}^2s_{{b_{12}}}^3 \cdots s_{{b_{12}}}^{2n} $ 。量子态的制备如图1a所示。3) Alice将
$ {S_A} $ 中Bell态的所有第一个粒子按原顺序形成序列$ {S_{A1}} = s_{{a_1}}^1s_{{a_1}}^2s_{{a_1}}^3 \cdots s_{{a_1}}^{2n} $ ;将$ {S_A} $ 中Bell态的所有第二个粒子按原顺序形成序列$ {S_{A2}} = s_{{a_2}}^1s_{{a_2}}^2s_{{a_2}}^3 \cdots s_{{a_2}}^{2n} $ 。并将$ p $ 个诱骗态粒子和序列$ {r_A} = r_A^1r_A^2r_A^3 \cdots r_A^n $ 中的$ n $ 个粒子随机插入序列$ {S_{A2}} $ 中,其中,诱骗态粒子是从集合$ \left\{|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle \right\} $ 中随机选取的。新序列记为$ S_{A2}^* $ ,Alice将它发给Bob,自己保留$ {S_{A1}} $ 。生成新粒子序列$ S_{A2}^* $ 和$ S_{B1}^* $ 如图1b所示。与此同时,Bob执行类似操作,得到序列
$ S_{B1}^* $ 和$ {S_{B2}} $ ,其中$ S_{B1}^* $ 也插入了诱骗态粒子和序列$ {r_B} $ 中的所有粒子。Bob将$ S_{B1}^* $ 发送给Alice,保留$ {S_{B2}} $ 。如图1c粒子序列的交换所示。4) 当Alice收到Bob发来的
$ S_{B1}^ * $ 后,Bob公布诱骗态粒子位置以及相应测量基。Alice对诱骗态粒子进行测量,并公布测量结果。Bob比较测量结果与诱骗态粒子的初始量子态,计算错误率。同时,当Bob收到Alice发来的$ S_{A2}^ * $ 后,Alice和Bob执行类似操作。然后Alice计算错误率。如果Alice和Bob计算的错误率都低于门限值[16],则认为信道是安全的,Alice和Bob可以继续进行下一步;如果Alice和Bob哪一方计算的错误率高于门限值,则停止该步骤并重新开始。
5) 当两方的信道都通过了安全检测后,就对双方进行身份认证。
当认证Alice身份时,由Alice公布
$ {r_A} $ 中所有粒子的位置和测量基,而Bob则对$ {r_A} $ 中所有粒子进行测量。然后Bob根据$ {r_A} $ 的测量结果和步骤1),得到相应二进制序列$ R_A' $ ,通过比较$ R_A' $ 与$ {R_A} $ 是否相等,来判断Alice的身份是否正确。通过对$ S_{B1}^ * $ 中的$ {r_B} $ 粒子执行类似操作,来判断Bob的身份是否正确。如果Alice和Bob双方都通过了身份认证,则可以继续进行协议的下一步,否则终止协议并重新开始。信道安全性检测与身份认证如图2所示。先测量诱骗态粒子,完成信道安全性检测后,再测量身份信息粒子,完成身份认证。
6) 去掉
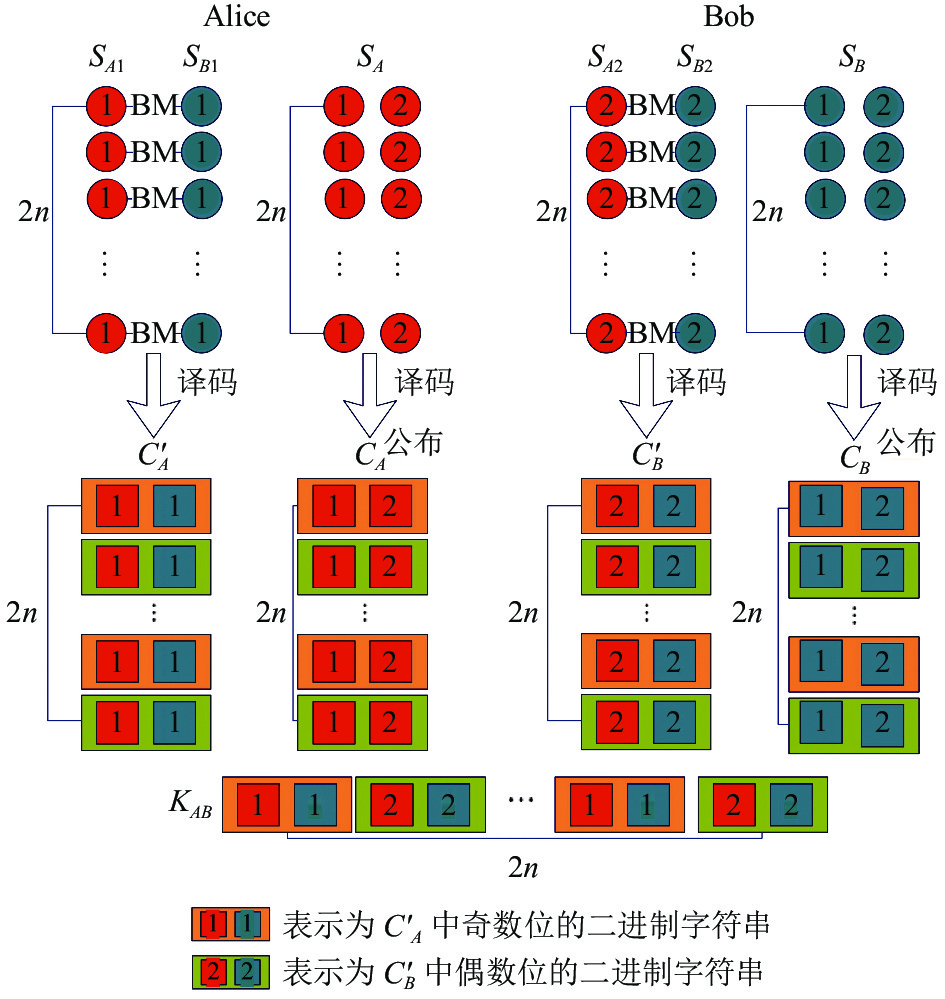
$ S_{B1}^* $ 中的$ {r_B} $ 和诱骗态粒子恢复序列$ {S_{B1}} $ 后,Alice对$ {S_{B1}} $ 和$ {S_{A1}} $ 中的对应粒子做Bell基测量,得到新序列$ S_A' = s_{{a_1}{b_1}}^1s_{{a_1}{b_1}}^2s_{{a_1}{b_1}}^3 \cdots s_{{a_1}{b_1}}^{2n} $ 。同时Bob执行类似操作,得到新序列$S_B' = s_{{a_2}{b_2}}^1 s_{{a_2}{b_2}}^2 s_{{a_2}{b_2}}^3 \cdots s_{{a_2}{b_2}}^{2n}$ 。7) Alice根据第1节中的编码规则将序列
$ {S_A} $ 和$ S_A' $ 转换为二进制序列$ {C_A} = C_{{a_1}{a_2}}^1C_{{a_1}{a_2}}^2C_{{a_1}{a_2}}^3 \cdots C_{{a_1}{a_2}}^{2n} $ 和$ C_A' = C_{{a_1}{b_1}}^1C_{{a_1}{b_1}}^2C_{{a_1}{b_1}}^3 \cdots C_{{a_1}{b_1}}^{2n} $ ;同时Bob执行类似操作将$ {S_B} $ 和$ S_B' $ 转换为二进制序列${C_B} = C_{{b_1}{b_2}}^1C_{{b_1}{b_2}}^2 C_{{b_1}{b_2}}^3 \cdots C_{{b_1}{b_2}}^{2n}$ 和$ C_B' = C_{{a_2}{b_2}}^1C_{{a_2}{b_2}}^2C_{{a_2}{b_2}}^3 \cdots C_{{a_2}{b_2}}^{2n} $ 。然后,Alice和Bob在经典信道公布$ {C_A} $ 和$ {C_B} $ 。8) Alice根据公式
$ {C_A} \oplus {C_B} = C_A' \oplus C_B' $ 和她拥有的$ C_A' $ 可以计算出$ C_B' $ ;同理Bob可以计算出$ C_A' $ 。那么他们协商的会话密钥是$ {K_{AB}} = {\text{\{ }}C_{{a_1}{b_1}}^1,C_{{a_2}{b_2}}^2, \cdots , C_{{a_1}{b_1}}^{2n - 1},C_{{a_2}{b_2}}^{2n}{\text{\} }} $ 。Bell态的测量与密钥协商如图3所示,其中BM表示Bell态的测量。 -
一个好的QKA协议应该既可以抵抗外部攻击,也可以抵抗内部攻击。
-
Alice和Bob在步骤1)、2)制备序列
$ {r_A} $ ,$ {r_B} $ ,$ {S_A} $ 和$ {S_B} $ ;在步骤3)传输序列$ S_{A2}^* $ 和$ S_{B1}^* $ ;在步骤4)测量序列$ S_{A2}^* $ 和$ S_{B1}^* $ 中的诱骗态粒子进行信道安全性检测;在步骤5)对序列$ S_{A2}^* $ 和$ S_{B1}^* $ 中的粒子$ r_A^i $ 和$ r_B^i $ 进行测量完成身份认证;在步骤6)~8)完成会话密钥协商。通过对协议的分析知,双方只在步骤3)进行了信息的传输,其他步骤只进行了量子态的制备和测量。身份假冒攻击:假设Eve想冒充Alice身份。由于Eve不知道Alice的身份信息序列
$ {R_A} $ ,他只能在步骤1)中随机制备粒子序列$ r_A' = r_A^{'1}r_A^{'2}r_A^{'3} \cdots r_A^{'n} $ 。然而在步骤5)的身份认证过程中,Bob测量$ r_A' $ 的结果和身份信息$ {R_A} $ 是无关的。如假设Alice的身份信息$ {R_A} = R_A^1 = 0 $ ,然而Eve并不知道$ R_A^1 $ ,他只能从集合$\{|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle\}$ 中随机选取粒子态,当他选择$ \left| 0 \right\rangle $ 态或$ \left| + \right\rangle $ 态时,Bob测量结果的编码为0;当他选择$ \left| 1 \right\rangle $ 态或$ \left| - \right\rangle $ 态时,Bob测量结果的编码为1。那么Eve冒充成功的概率为$ {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2} $ ,当$ {R_A} $ 长度为$ n $ 时,最终Eve冒充成功的概率为$ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right)^n} $ 。当$ n $ 足够大时,Eve冒充成功的概率$ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right)^n} $ 趋于0。同理当Eve冒充Bob身份时,Alice进行类似操作也容易判断出Eve的身份是假冒的。针对会话密钥的攻击:假设Eve想窃取会话密钥,他只能在双方通信时,即在步骤3)对序列
$ S_{A2}^* $ 和$ S_{B1}^* $ 执行特洛伊木马攻击、测量−重发攻击、截获−重发攻击或纠缠−测量攻击。由于序列$ S_{A2}^* $ 和$ S_{B1}^* $ 在本协议中仅被传输了一次,因此Eve无法成功实现两种特洛伊木马攻击[17-19]。若Eve进行测量−重发攻击、截获−重发攻击或纠缠−测量攻击,然而Eve的操作会影响序列$ S_{A2}^* $ 和$ S_{B1}^* $ 中诱骗态粒子的状态[12],从而Alice和Bob在步骤4)的信道安全性检测中就能发现Eve的攻击。 -
当Alice和Bob通过了身份认证后,他们的身份就是合法的。在后续密钥中,双方交换序列
$ S_{A2}^* $ 和$ S_{B1}^* $ ,并分别测量序列对$ \left( {{S_{A1}},{S_{B1}}} \right) $ 和$ \left( {{S_{A2}},{S_{B2}}} \right) $ 。由式(2)和表1给出的纠缠交换关系可知,Alice和Bob的测量结果是在4种Bell态中等概率出现的。即双方的测量结果是随机的,Alice和Bob都不能决定他们的测量结果。因此,双方都不能成功执行参与者攻击。 -
QKA协议的量子比特效率公式[20]定义为
$ \eta = {c \mathord{\left/ {\vphantom {c {\left( {q + b} \right)}}} \right. } {\left( {q + b} \right)}} $ ,其中,$ c $ 表示协商出的会话密钥的比特数量,$ q $ 表示协议中用到的量子比特总数,$ b $ 表示用于解码的经典信息。因为本文QKA协议中用到的Bell态数量为
$ 4n $ ,诱骗态量子比特数量为$ 2p $ ,身份认证粒子的比特数量为$ 2n $ ,经典解码信息为$ b = 4n + 4n = 8n $ ,得到的会话密钥比特数量为$ c = 4n $ 。所以本文QKA的量子比特效率为$ \eta = {{4n} \mathord{\left/ {\vphantom {{4n} {\left( {4n \times 2 + 2p + 2n + 8n} \right)}}} \right. } {\left( {4n \times 2 + 2p + 2n + 8n} \right)}} $ 。又因为身份认证粒子是随机插入的,可起部分诱骗态粒子的作用,所以可令$ p = n $ 。当$ p = n $ 时,效率为$ \eta = 4n/20n = 20\% $ 。它与已有互认证的QKA协议的比较可以参见表2。根据表2知本文的QKA协议在量子比特效率方面也较高。 -
本文利用Bell态提出了一个两方的互认证量子密钥协商协议,它无需第三方的参与就能实现参与者的身份互认证和密钥协商,协议的步骤简单且只需一次交互的量子通信。 安全性分析证明了这个QKA协议可以有效抵抗外部攻击和内部攻击。与已有的互认证QKA协议相比较,本文提出的新的互认证QKA协议不但有较高的量子比特效率,而且仅用到了单粒子测量和Bell态测量,在现有技术的基础上更易实现。
Two-Party Mutual Authentication Quantum Key Agreement Protocol Based on Bell States
doi: 10.12178/1001-0548.2022008
- Received Date: 2021-12-30
- Accepted Date: 2022-06-13
- Rev Recd Date: 2022-03-28
- Available Online: 2022-07-11
- Publish Date: 2022-07-09
-
Key words:
- Bell state /
- entanglement exchange /
- mutual identity authentication /
- quantum cryptography /
- quantum key agreement
Abstract: In order to solve the problem of complicated steps and large communication volume caused by the participation of trusted or semi-trusted third parties in the existing mutual authentication quantum key agreement protocols, a new two-party quantum key agreement protocol is proposed based on Bell states and their entangled exchange properties. The key agreement protocol can realize identity mutual authentication and fair key agreement between participants without the participation of trusted or semi-trusted third parties, thus reducing the communication complexity of the protocol. The security analysis shows that its identity authentication process can resist impersonation attack, and its key agreement process can resist external attacks and participant attacks. In addition, compared with the existing mutual authentication quantum key agreement protocols, the quantum bit efficiency of the protocol is also higher, and its quantum state preparation and measurement are easier to achieve with existing technologies.
| Citation: | HE Yefeng, DI Man, PANG Yibo, YUE Yuru, LI Guoqing, LIU Jixiang. Two-Party Mutual Authentication Quantum Key Agreement Protocol Based on Bell States[J]. Journal of University of Electronic Science and Technology of China, 2022, 51(4): 488-492. doi: 10.12178/1001-0548.2022008 |

 ISSN
ISSN 























































































































































 DownLoad:
DownLoad: