A Constructive Learning Differential Evolution Algorithm for Partially Separable Function Optimization Problems

本文引入差分分组(differential grouping, DG2)^[14]策略，基于算法SHADE(success-history based adaptive DE)^[7]进行改进，以下分别进行介绍。

SHADE算法包含初始化、变异、交叉和选择等步骤。首先在问题的可行域中随机产生${{\rm{NP}}} $个$D$维向量构成初始种群：

变异操作是DE算法的核心操作，目前已有许多经典的变异策略，SHADE算法采用DE/current-to-pbest/1变异策略：

式中，$t$为当前进化代数；$ {r_1} $、$ {r_2} $随机从$[1,{{\rm{NP}}} ]$中选取且与$i$互不相等；$F$为缩放因子；$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $随机从${{\rm{NP}}} \times p(p \in [0.11,0.2])$个当前种群的最优解中选取。SHADE采用一个外部存档存储保存部分较差的个体以增加种群的多样性。式(2)表明DE/current-to-pbest/1变异策略包含了差分扰动和向优秀解学习两部分，$ F({\boldsymbol{X}}_{r1}^t - {\boldsymbol{X}}_{r2}^t) $为扰动项，且$ {\boldsymbol{X}}_{r2}^t $从外部存档和当前种群的合集中随机选取。$ F({\boldsymbol{X}}_{{{\rm{pbest}}} }^t - {\boldsymbol{X}}_i^t) $为向当前优秀解学习项。如果变异向量$ V_i^t $超出问题的可行域，则执行以下操作：

交叉操作将变异向量和父代向量进行交叉，形成实验向量：

式中，$ {{\rm{Cr}}} $是交叉概率；$ {j_{{\rm{rand}}}} $从$ \left[ {1,{D} } \right] $之间随机选取。然后从目标向量和实验向量中选择适应度较小(以最小化问题为例)的个体进入下一代种群，如下所示：

参数控制机制对算法的搜索性能起着至关重要的作用，SHADE采用一种基于成功历史的自适应策略，将进化过程中成功的$H$个缩放因子$F$和交叉概率$ {{\rm{Cr}}} $保存在${M_{{{{\rm{Cr}}}}}}$和${M_F}$中以供选择。参数$F$服从柯西分布$C({\mu _F},0.1)$，${\mu _F}$的初值为0.5，更新如下：

式中，${S_F}$为子代成功取代父代时参数$F$的集合，$ {\rm{mea}}{{\rm{n}}_L}({S_F}) $为Lehmer均值。类似地，交叉概率$ {{\rm{Cr}}} $服从正态分布$N({\mu _{{{{{\rm{Cr}}}}} }},0.1)$，${\mu _{{{{{\rm{Cr}}}}} }}$的初值为0.5，更新如下：

式中，${S_{ {\rm{Cr}}}}$为子代成功取代父代时参数${{\rm{Cr}}}$的集合；${{{\rm{mean}}} _A}({S_{ {\rm{Cr}} }})$为算术平均。

基于“分而治之(divide-and-conquer)”的思想，分组是进化算法解决复杂函数优化问题的一种重要策略，该策略将复杂问题划分为多个相对简单的子问题。有效的分组策略可以解耦多个存在交互关系的决策变量，最小化不同子问题之间的依赖关系^[15]。

函数$f({\boldsymbol{X}}):{\mathbb{R}^n} \to \mathbb{R}$是部分可分离问题，当且仅当：

式中，${\boldsymbol{X}} = ({x_1},{x_2}, \cdots, {x_n})$是$n$维决策向量；${{\boldsymbol{X}}_1}, {{\boldsymbol{X}}_2}, \cdots, {{\boldsymbol{X}}_m}$是向量$ {\boldsymbol{X}} $的不相交子向量，$2 \leqslant m \leqslant n$。

函数$f({\boldsymbol{X}})$满足如下条件则称之为部分加性可分离：

差分分组方法检测决策变量之间的交互关系，如果存在交互则将其分在一组，否则被分在不同的组，如果一个决策变量与其他所有变量都不存在交互，则该变量为独立变量。分组方法定义如下。

$f({\boldsymbol{X}})$是部分加性可分离函数，$ \forall a,{b_1},{b_2},{x_p},{x_q} \in \mathbb{R} $，$ a,{b_1} \ne {b_2} $，$ \delta \in \mathbb{R} $，$ \delta \ne 0 $，如果以下式子成立，则${x_p}$和${x_q}$存在交互关系，是不可分决策变量。

否则，${x_p}$和${x_q}$为可分离决策变量。

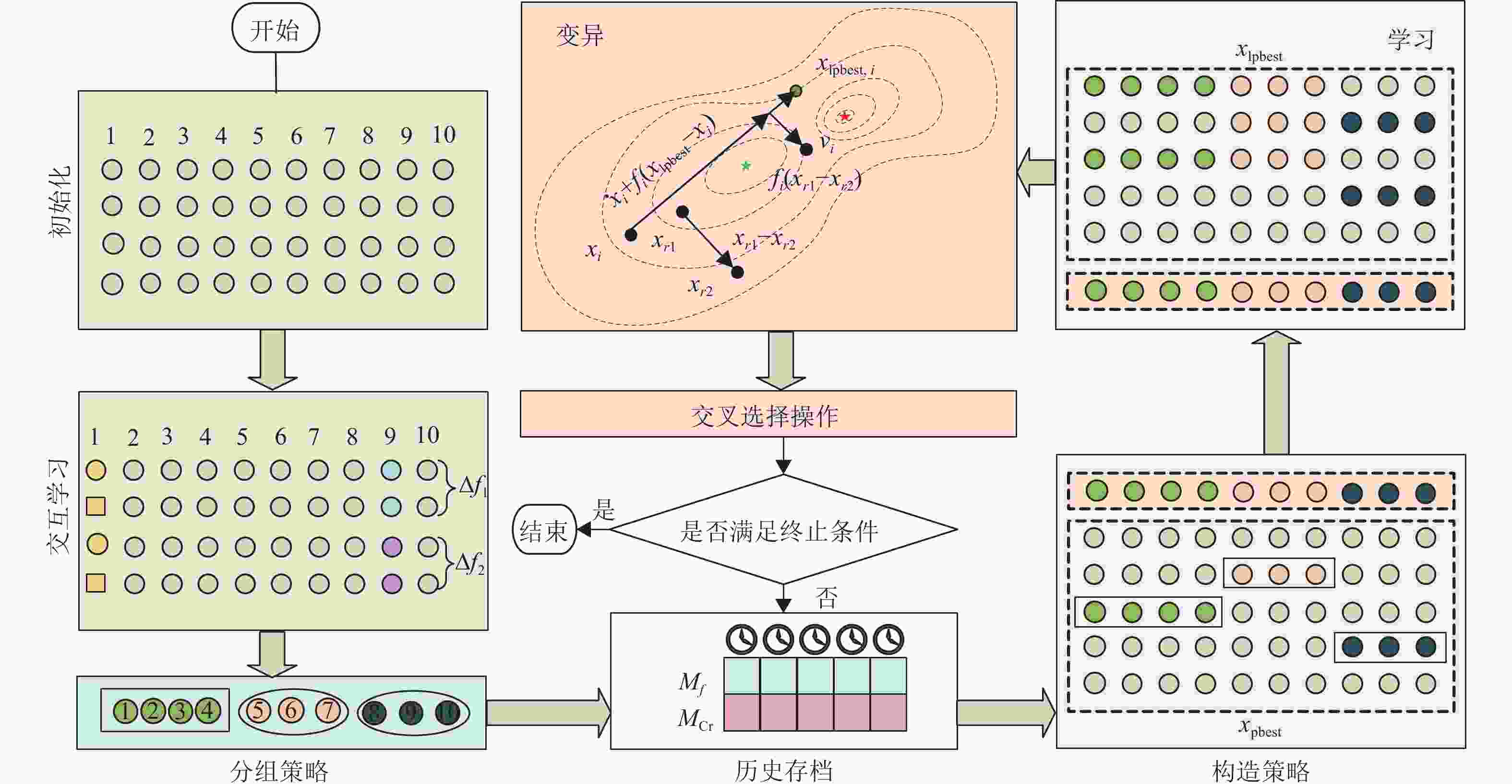
CLSHADE的核心步骤主要包含3部分：分组、构造学习策略及SHADE。首先对复杂问题通过差分分组检测决策变量间的耦合关系，将原始问题分解为多个相互独立的分组。然后基于母体算法SHADE通过构造学习策略提高其搜索能力。算法总体框架如图1所示。

问题分组策略检查每个决策变量与其他决策变量之间是否存在交互关系，循环上述过程直到完成所有变量之间交互关系的判断，具体如算法1所示。其中$f({\boldsymbol{X}})$为目标函数，$ {x^{{\rm{min}}}} $和$ {x^{{\rm{max}}}} $为决策变量上下界，${{\rm{ones}}} (1,D)$函数用于生成$D$维全1向量。

为判断决策向量的第$i$维和第$j$维是否存在交互，初始化两个决策向量${{\boldsymbol{x}}_1}$和${{\boldsymbol{x}}_2}$，${{\boldsymbol{x}}_1}$初始化为决策变量下界，${{\boldsymbol{x}}_2}$除第$j$维初始化为上界外，其他维度和${{\boldsymbol{x}}_1}$一样初始化为下界，然后根据式(10)和(11)计算$ {\varDelta _1} $和$ {\varDelta _2} $，根据既定阈值$\varepsilon $判断交互关系$ (\varepsilon = {10^{ - 3}}) $，最后输出决策变量分组结果。

算法1　分组算法DG

输入：$f({\boldsymbol{X}})$

输出：分组结果${{\rm{groups}}} $

初始化：$S \leftarrow \{ 1,2, \cdots ,D\} $,${{\rm{sep}}} \leftarrow \{ \} $,${{\rm{groups}}} \leftarrow \{ \} $

For $i \in S$ do

　${{\rm{group}}} \leftarrow \{ i\}$

　For $j \in S \wedge i \ne j$ do

　　${{\boldsymbol{x}}_1} \leftarrow {x^{{\rm{min}}}} \times {{\rm{ones}}} (1,D)$,${{\boldsymbol{x}}_2} \leftarrow {{\boldsymbol{x}}_1}$

　　${{\boldsymbol{x}}_2}(i) \leftarrow {x^{{\rm{max}}}}$,${\varDelta _1} = f({{\boldsymbol{x}}_1} - {{\boldsymbol{x}}_2})$

　　${{\boldsymbol{x}}_1}(j) \leftarrow 0$,${{\boldsymbol{x}}_2}(j) \leftarrow 0$,${\varDelta _2} = f({{\boldsymbol{x}}_1} - {{\boldsymbol{x}}_2})$

　　　//初始化并根据式(10)～式(11)计算$\varDelta $

　　If $\left| {{\varDelta _1} - {\varDelta _2}} \right| > \varepsilon $ then

　　　${\text{group}} \leftarrow {{\rm{group}}} \cup \{ j\}$

　　　//如果相关则放入一组

　　End

　End

　$S \leftarrow S - {{\rm{group}}}$ //相关则从$S$中移除

　If ${{\rm{length}}} ({{\rm{group}}} ) = 1$ Then

　　$ {{\rm{seps}}} \leftarrow {{\rm{seps}}} \cup {{\rm{group}}} $ //保存独立变量

　Else

　　${{\rm{groups}}} \leftarrow {{\rm{groups}}} \cup {{\rm{group}}}$

　　//在${{\rm{groups}}} $中加入新识别的分组

　End

End

${{\rm{groups}}} \leftarrow {{\rm{groups}}} \cup \{ {{\rm{seps}}} \} $//输出结果

变异策略是DE算法的核心操作，DE/best/1、DE/best/2以及SHADE采用的DE/current-to-best/1都向当前种群的优秀解$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $学习，利用$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $中潜在的有用信息引导种群的搜索。然而，$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $有可能存在部分维度优秀，部分维度一般的情况。一个简单的例子，假设给定一个最小化优化函数$ f(x) = {({x_1} - {x_2})^2} + {({x_3} - {x_4})^2} $，$ x \in {[0,1]^4} $，基于交互关系决策变量显然可以分为两组$\{ {x_1},{x_2}\} $，$\{ {x_3},{x_4}\} $。对于3个$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $：$(0.8,0.4,0.6,0.4)$，$(0.6,0.4,0.8,0.4)$和$(0.6,0.4,0.6,0.4)$，前两个解都在部分分组维度上优秀，而第三个解在全部分组维度上优秀，最终最优解为$(0.6,0.4,0.6,0.4)$。

得益于分组结构，构造一个$ {\boldsymbol{X}}_{{{\rm{cpbest}}} }^t $，组合多个个体不同分组维度的优秀信息，具体如下：

式中，$ {\boldsymbol{X}}_{{{\rm{pbest}}} ,{{i}}}^t $为第$i$个分组的优秀解。新的变异策略结合DE/current-to-best/1策略和构造学习策略(constructive learning strategy, CLS)，如下所示：

式中，$ {\boldsymbol{X}}_{{{\rm{lpbest}}} }^t $以概率$ {{{{Pc}}} _i} $向构造的$ {\boldsymbol{X}}_{{{\rm{cpbest}}} }^t $学习，如：

式(15)为学习概率$ {{{{Pc}}} _{{i}}} $的定义，其中，$ \varphi $为学习因子；${{{{\rm{ps}}}}} $为$ {\boldsymbol{X}}_{{{\rm{pbest}}} }^t $的数量；${{\rm{rand}}} $是$[0,1]$之间的随机数。可以看出$ {{{{Pc}}} _{{i}}} $单调递增，是考虑到随着进化过程的推进，$ {\boldsymbol{X}}_{{{\rm{cpbest}}} }^t $逐步向问题最优解区域靠近，因此在进化后期比进化前期赋予相对较高的学习概率。考虑到学习因子$ \varphi $对算法性能的影响，因此在本文实验部分和其他重要参数一起进行正交实验分析。构造学习策略具体流程如算法2所示。

算法2　构造学习策略CLS

输入：$f({\boldsymbol{X}})$, ${{\rm{groups}}} = \{ {{{\rm{group}}} _1},{{{\rm{group}}} _2}, \cdots ,{{{\rm{group}}} _m}\}$

输出：$ {{\boldsymbol{X}}_{{{\rm{lpbest}}} }} $

For $i = 1:{{\rm{ps}}}$ do //构造${{\boldsymbol{X}}_{{{\rm{cpbest}}} ,{\rm{i}}}}$过程

　For $j = 1:m$ do

　　$\tau = {{\rm{groups}}} (j)$ //第$j$个分组

　　${{\rm{ind}}} _1^j = \left\lceil {{{\rm{rand}}} (0,1) \times {{\rm{ps}}} } \right\rceil$

　　${{\rm{ind}}} _2^j = \left\lceil {{{\rm{rand}}} (0,1) \times {{\rm{ps}}} } \right\rceil$ //向上取整

　　If $f({{\boldsymbol{X}}_{{{\rm{pbest}}} }}({{\rm{ind}}} _1^j)) \leqslant f({{\boldsymbol{X}}_{{{\rm{pbest}}} }}({{\rm{ind}}} _2^j))$

　　　${\boldsymbol{X}}_{{{\rm{cpbest}}} ,{\rm{i}}}^\tau = {{\boldsymbol{X}}_{{{\rm{pbest}}} }}({{\rm{ind}}} _1^j)$

　　Else

　　　${\boldsymbol{X}}_{{{\rm{cpbest}}} ,{\rm{i}}}^\tau = {{\boldsymbol{X}}_{{{\rm{pbest}}} }}({{\rm{ind}}} _2^j)$

　　End

　End

End //基于分组构造最优解

For $i = 1:{{\rm{ps}}}$ do //${\boldsymbol{X}}_{{{\rm{lpbest}}} ,{{i}}}^t$的生成

　For $j = 1:m$ do

　　$\tau = {{\rm{groups}}} (j)$

　　If ${{\rm{rand}}} < {{{{Pc}}} _{{i}}}$

　　　${\boldsymbol{X}}_{{{\rm{lpbest}}} ,{{i}}}^\tau = {\boldsymbol{X}}_{{{\rm{cpbest}}} ,{{i}}}^\tau$

　　Else

　　　${\boldsymbol{X}}_{{{\rm{lpbest}}} ,{{i}}}^\tau = {\boldsymbol{X}}_{{{\rm{pbest}}} ,{{i}}}^\tau$

　　End

　End

End //向构造的最优解学习

CLSHADE首先采用算法1对问题分组，然后在SHADE算法中使用算法2设计的构造策略迭代寻优，具体流程如算法3所示。

算法3　CLSHADE

输入：$f({\boldsymbol{X}})$，维数$D$

输出：最优解${{\boldsymbol{X}}_{{{\rm{best}}} }}$

初始化：${{\rm{NP}}} = 18D$; ${{\boldsymbol{X}}^0} = ({\boldsymbol{X}}_1^0,{\boldsymbol{X}}_2^0, \cdots ,{\boldsymbol{X}}_{{{\rm{NP}}} }^0)$; $t = 0$

　　　　$H = 5$; ${M_{{{{{\rm{Cr}}}}} ,{{i}}}} = 0.5$, ${M_{{{F}},{{i}}}} = 0.5$;

${{\rm{groups}}} = {{\rm{DG}}} (f({\boldsymbol{X}}),{{\boldsymbol{X}}^0})$ //采用算法1进行分组

Repeat

　　${S_{{{\rm{CR}}} }} = \phi$, ${S_F} = \phi $

　　${{\boldsymbol{X}}_{{{\rm{lpbest}}} }} = {{\rm{CLS}}} (f({\boldsymbol{X}}),{{\rm{groups}}} )$

　　　　//采用算法2实施构造学习

　　For $i = 1:{{\rm{NP}}}$ do

　　　$k = {{\rm{rand}}} [1,H]$ //从历史存档中随机选择

　　　${{{\rm{CR}}} _i} = {{{\rm{rand}}n} _i}({M_{{{\rm{Cr}}} ,{{k}}}},0.1)$

　　　${F_i} = {{{\rm{rand}}c} _i}({M_{{{{F}}} ,{{k}}}},0.1)$

　　　${p_i} = {{\rm{rand}}} [{p_{\min }},0.2]$

　　　采用式(13)进行变异操作

　　　采用式(4)进行交叉操作

　　　采用式(5)进行选择操作

　　End

　　更新${M_{{{{{\rm{Cr}}}}} ,{{k}}}}$,${M_{{{{F}}} ,{{k}}}}$

　　$t{\text{ + + }}$ //迭代次数递增

Until 达到算法终止条件

本文实验环境为：Windows 10操作系统；Intel (R) Core (TM) i7-6700 CPU @ 3.40 GHz处理器；8 GB内存；基于MATLAB实现。比较算法的控制参数按照相应文献的建议进行设置。选取CEC 2017^[16]标准测试集的变量部分可分函数并在10D、30D上采用相同的评价准则进行实验。经过实验发现CEC 2017标准测试函数${f_1} \sim {f_{20}}$为部分变量部分可分函数，因此选用${f_1} \sim {f_{20}}$作为测试函数。

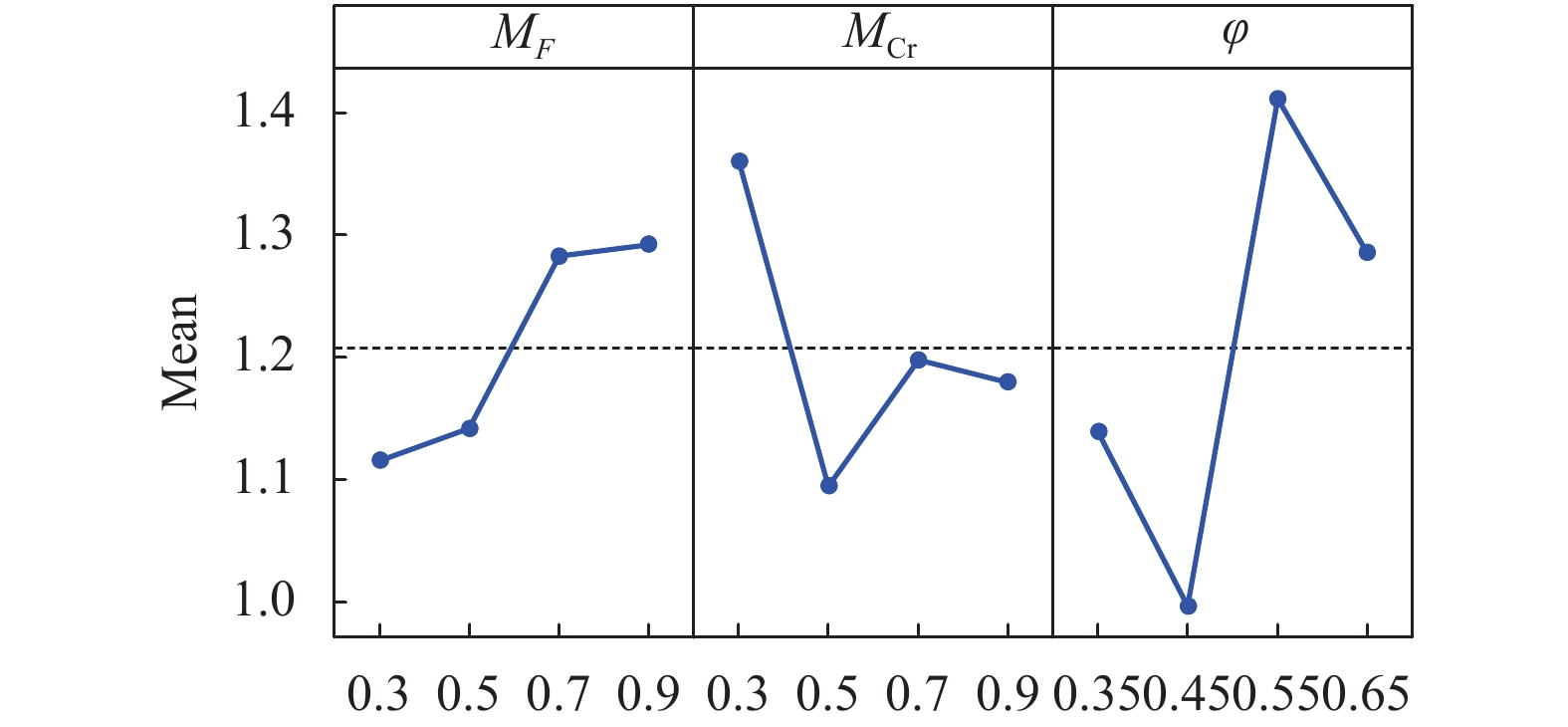
CLSHADE算法有3个关键的参数：变异因子${M_F}$、交叉概率${M_{{\rm{Cr}}}}$和学习因子$\varphi $，其初始取值的设定对算法的性能有重要影响，本文采用实验设计方法DOE(design of experiment)^[17]分析其对算法性能的影响并最终确定相应的初始取值。表1为每个参数的水平值设置。

表1参数的所有可能组合数为$4 \times 4 \times 4=64$，每个参数组合独立运行10次以确保实验具有统计学意义。对实验结果进行多元方差分析(multivariate analysis of variance, MANOVA)，结果如表2所示。

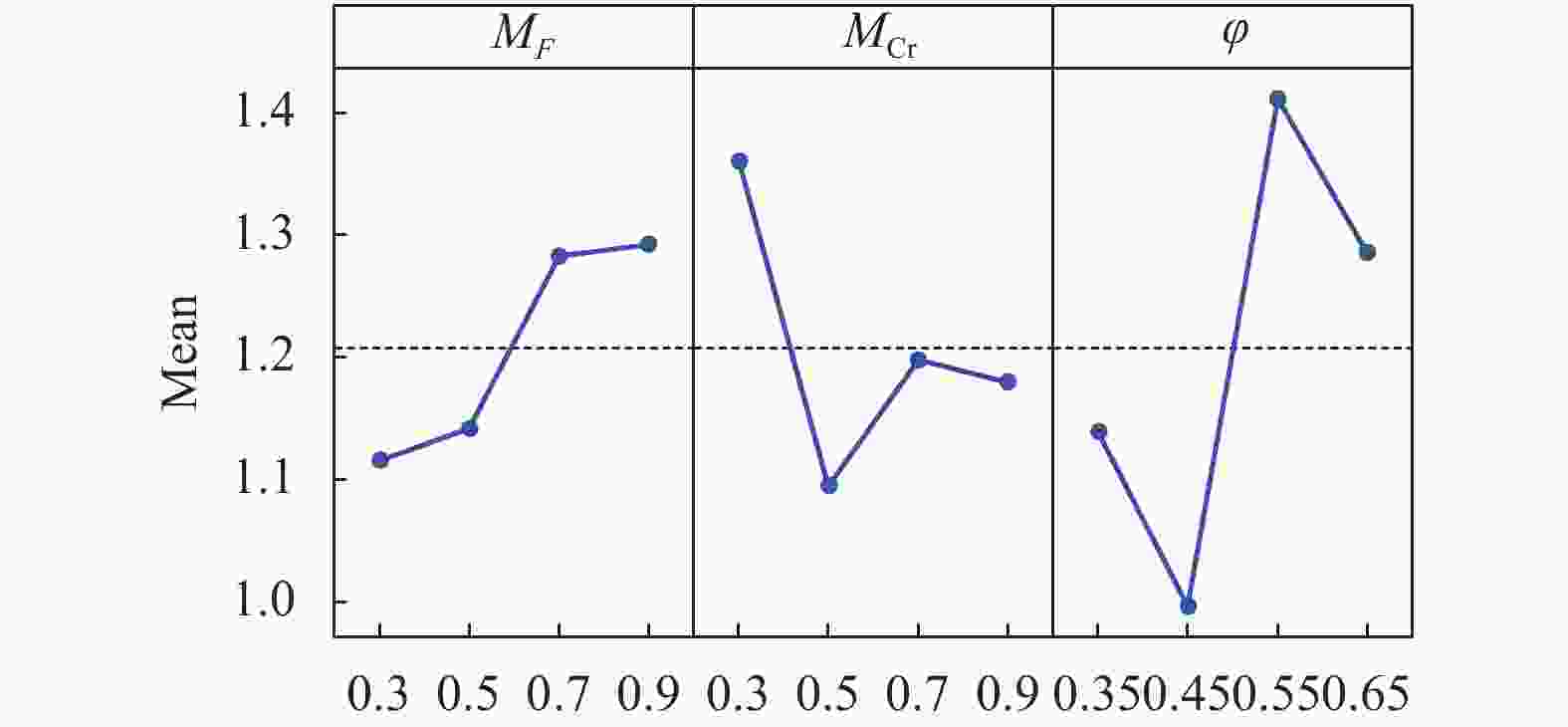
从表2可以看出，参数$\varphi $对应的F-ratio最大，即参数$\varphi $对CLSHADE的平均性能影响最大。 由于算法两个参数之间的$p$值大于0.05，所以CLSHADE中两个参数之间没有交互作用。参数主效应图如图2所示，因此选取参数取值组合：${M_F} = 0.3$, ${M_{{{{{\rm{Cr}}}}} }} = 0.5$, $\varphi = 0.45$。其他CLSHADE算法中涉及的所有其他非关键参数都与SHADE保持一致。

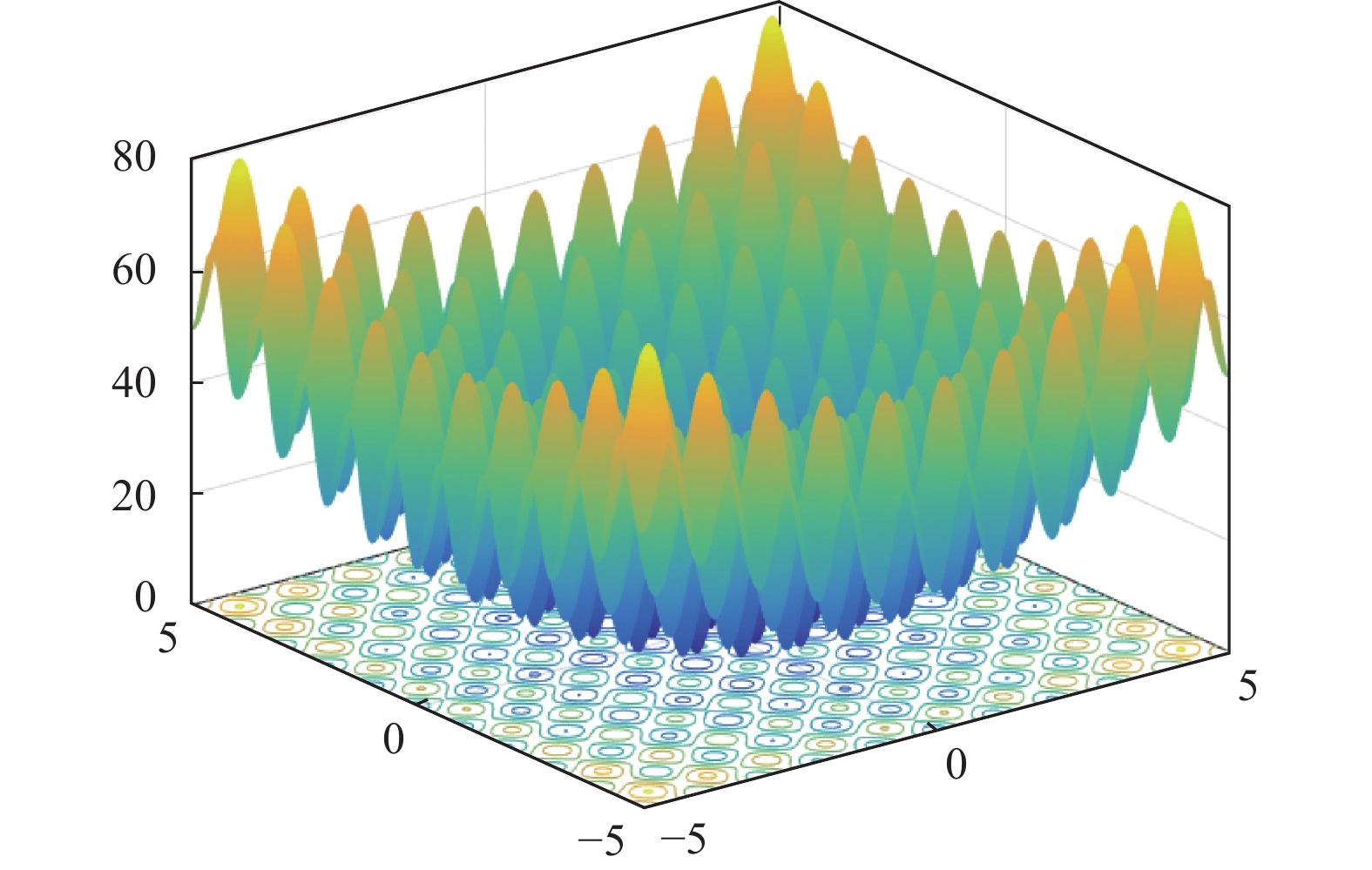
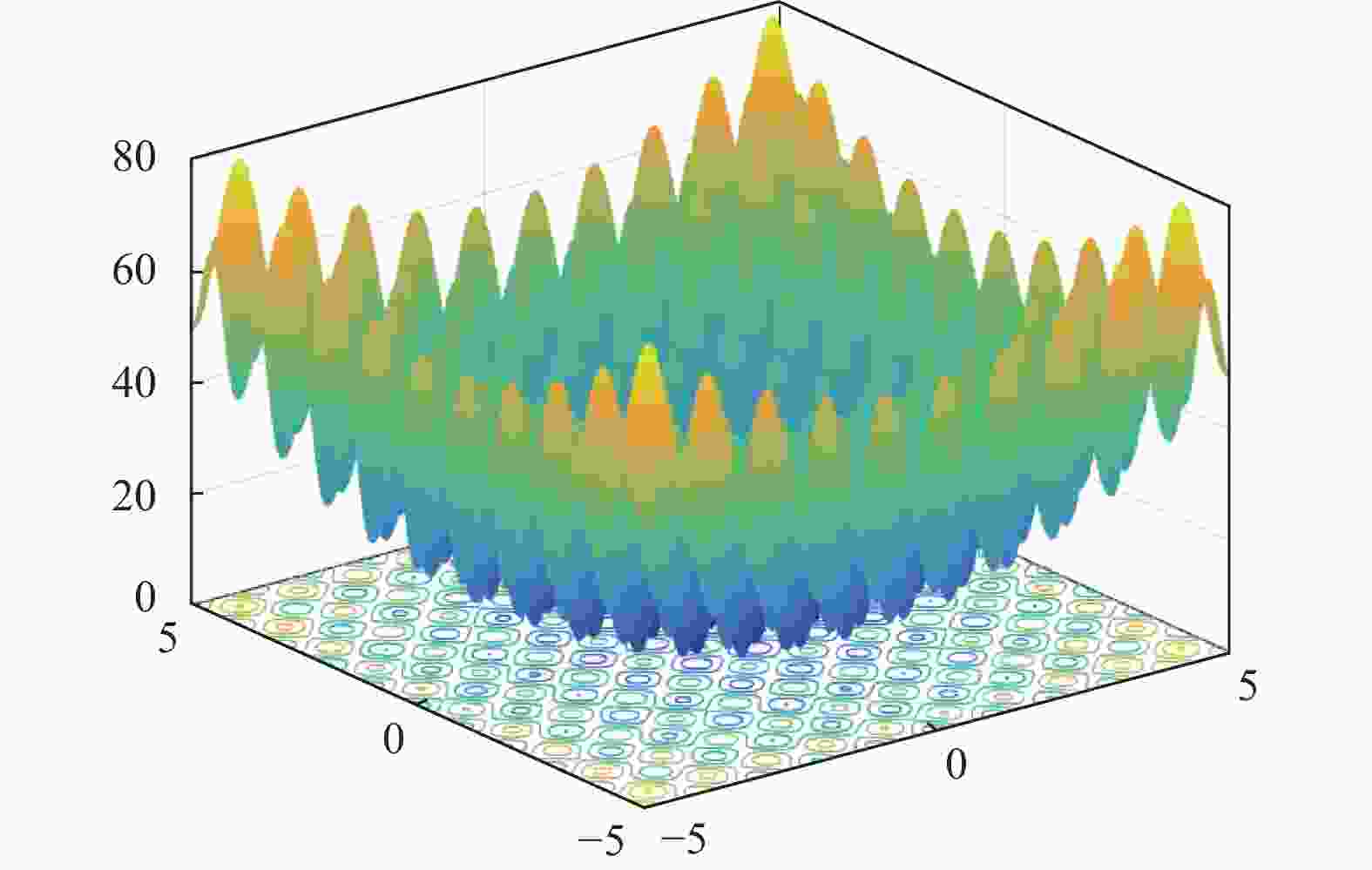
为通过具体函数观察CLSHADE的运行机制，以求解CEC 2017测试集的${F_5}({\boldsymbol{x}})$(shifted and rotated rastrigin’s function)函数为例进行说明。从图3所示Rastrigin’s函数的适应度地形图可以看出，该函数具有多模及多个局部最优等复杂特性。

CEC 2017对其进行旋转平移定义如下：

以$D = 6$为例，其旋转矩阵${\boldsymbol{M}}$和平移向量${\boldsymbol{o}}$分别为：

采用算法1进行对Rastrigin’s函数进行分组，共分为3个组，分别是${{{\rm{group}}} _1} = \{ {x_1},{x_2}\} $, ${{{\rm{group}}} _2} = \{ {x_3},{x_6}\} $, ${{{\rm{group}}} _3} = \{ {x_4},{x_5}\} $。采用构造学习策略后$F({\boldsymbol{x}})$的值如表3所示，显然得到了一个更有潜力的优秀解，从而加快了算法的收敛速度，并提高了解的精度。

为验证CLSHADE算法的性能，选取SHADE^[7]、AMECoDEs^[18]、HS-ES^[19]和EBLSHADE^[20]作为比较算法。所有实验在每个测试问题上独立运行51次，计算均值和标准差(Mean_std)，实验结果如表4(10维)和表5(30维)所示。

表4列出了10维问题的实验结果，可以看出所有算法在$ {f_1} \sim {f_4}、{f_9} $等5个函数上都找到了相同的最优解，在其余15个函数上CLSHADE有7个函数的结果优于其他算法，3个函数和部分其他算法找到相同的最优解，在其余函数如${f_5}、{f_{13}}$和${f_{19}}$上，CLSHADE也与求解性能最优算法的结果没有显著性差异。综上所述，CLSHADE在10维问题上的总体表现优于其他对比算法。

表5为30维问题的实验结果，所有算法在函数$ {f_1} \sim {f_3} $、$ {f_9} $上取得相同的最优解，在$ {f_6} $上CLSHADE和HS-ES、EBLSHADE都获得最优解，在剩余的15个函数中，CLSHADE在10个函数上优于其他算法，3个函数上与表现最优算法接近。总体来说，CLSHADE在30维问题上表现优秀。

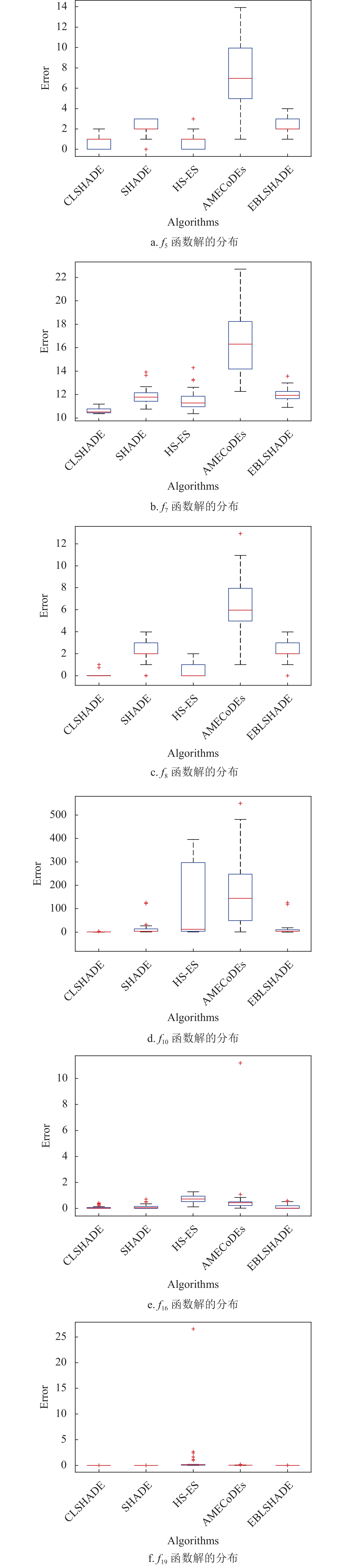
为进一步比较和分析所有算法的性能，本文以10维问题为例，通过收敛图观察算法的搜索过程(收敛性)，通过盒图考察最优解的分布情况(稳定性)，最后用Wilcoxon检验分析算法的统计学特性，结果如图4～图5及表6所示。

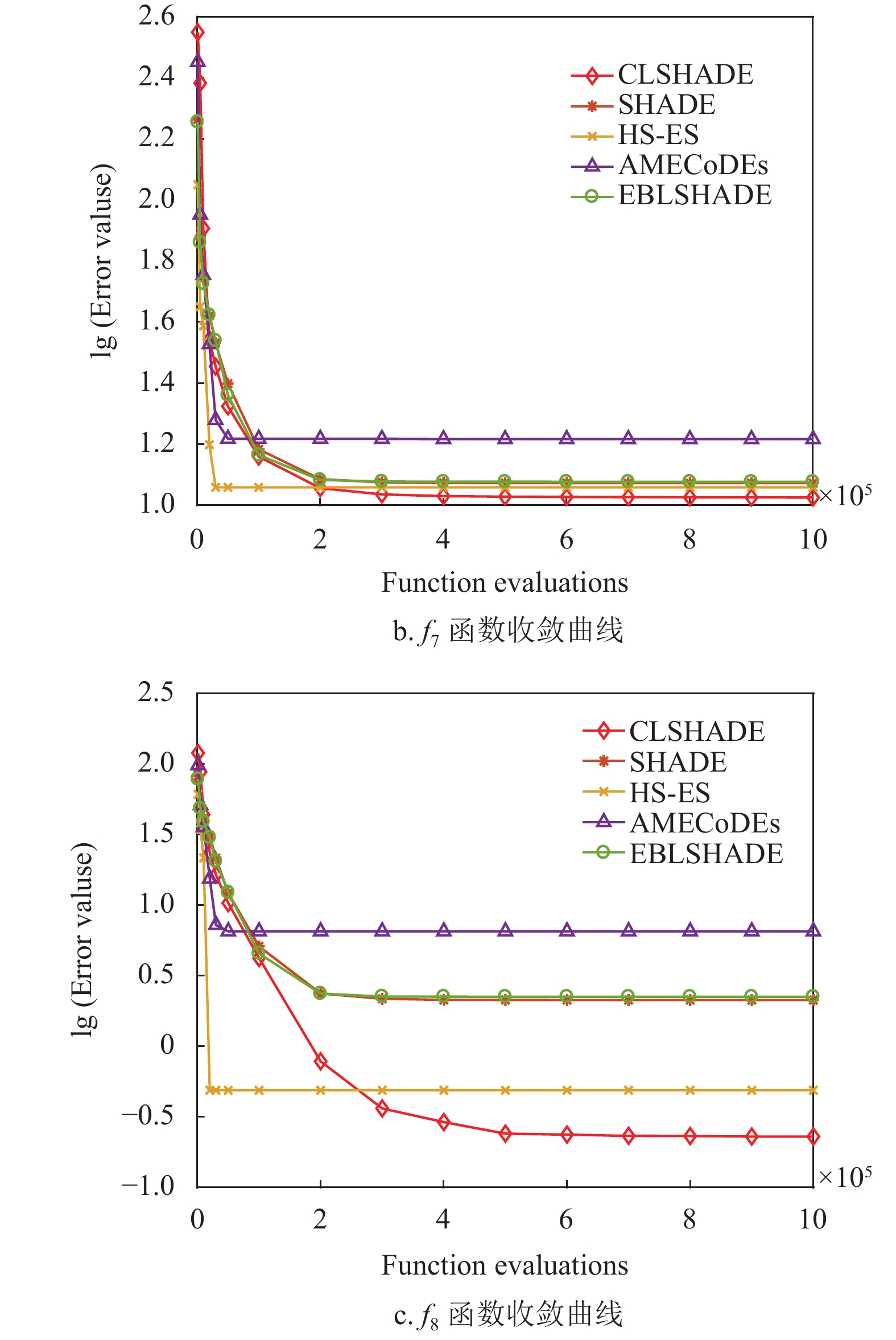
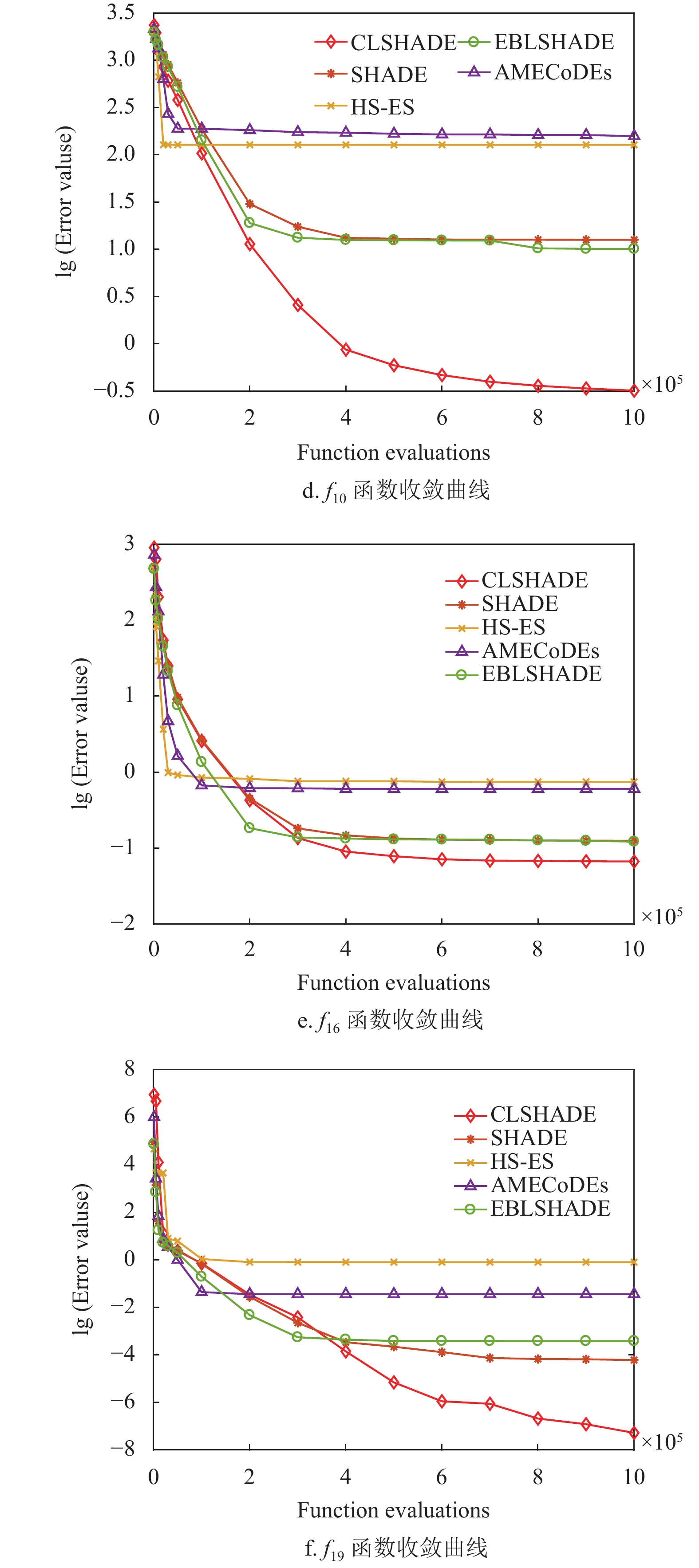
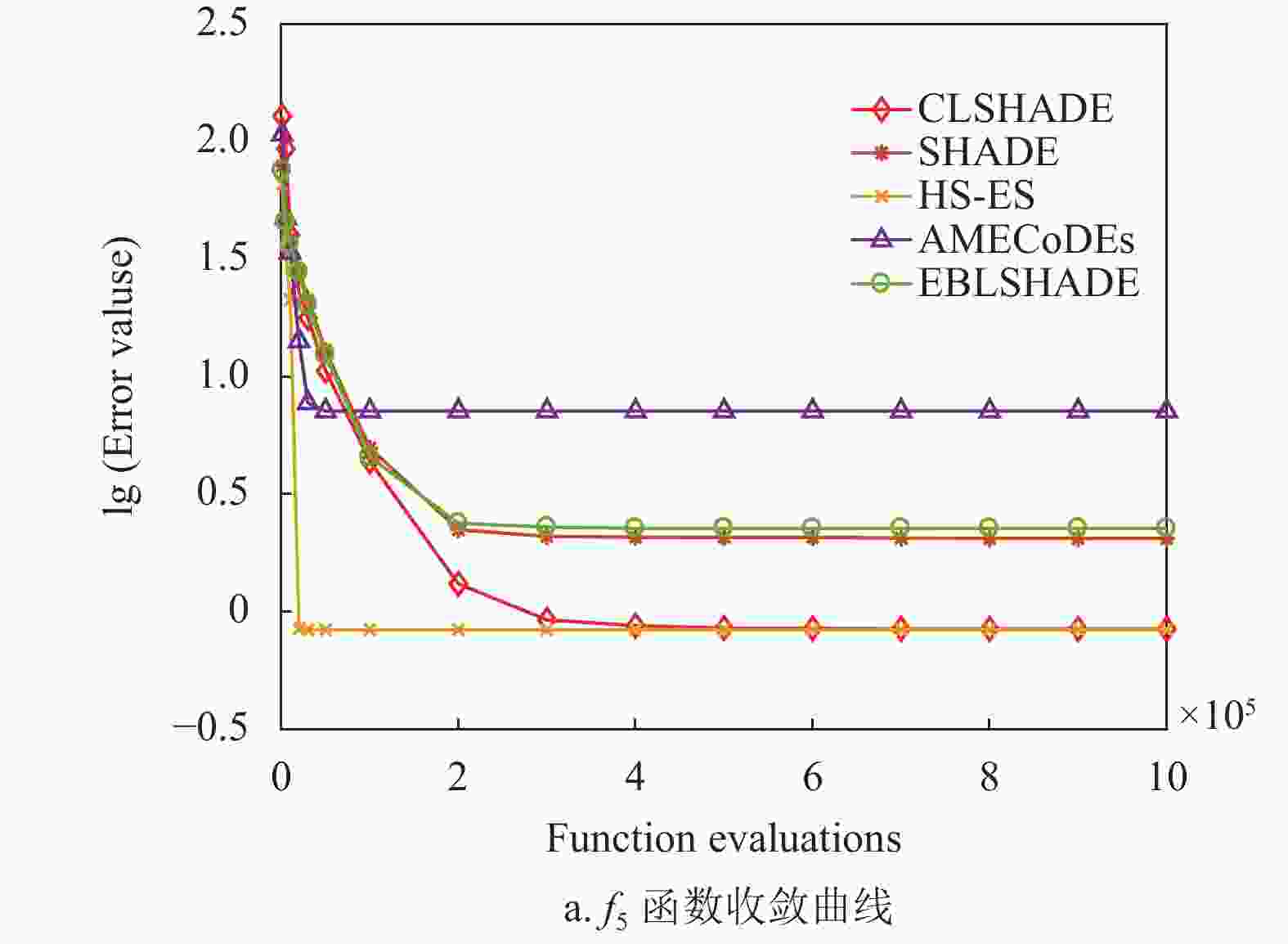
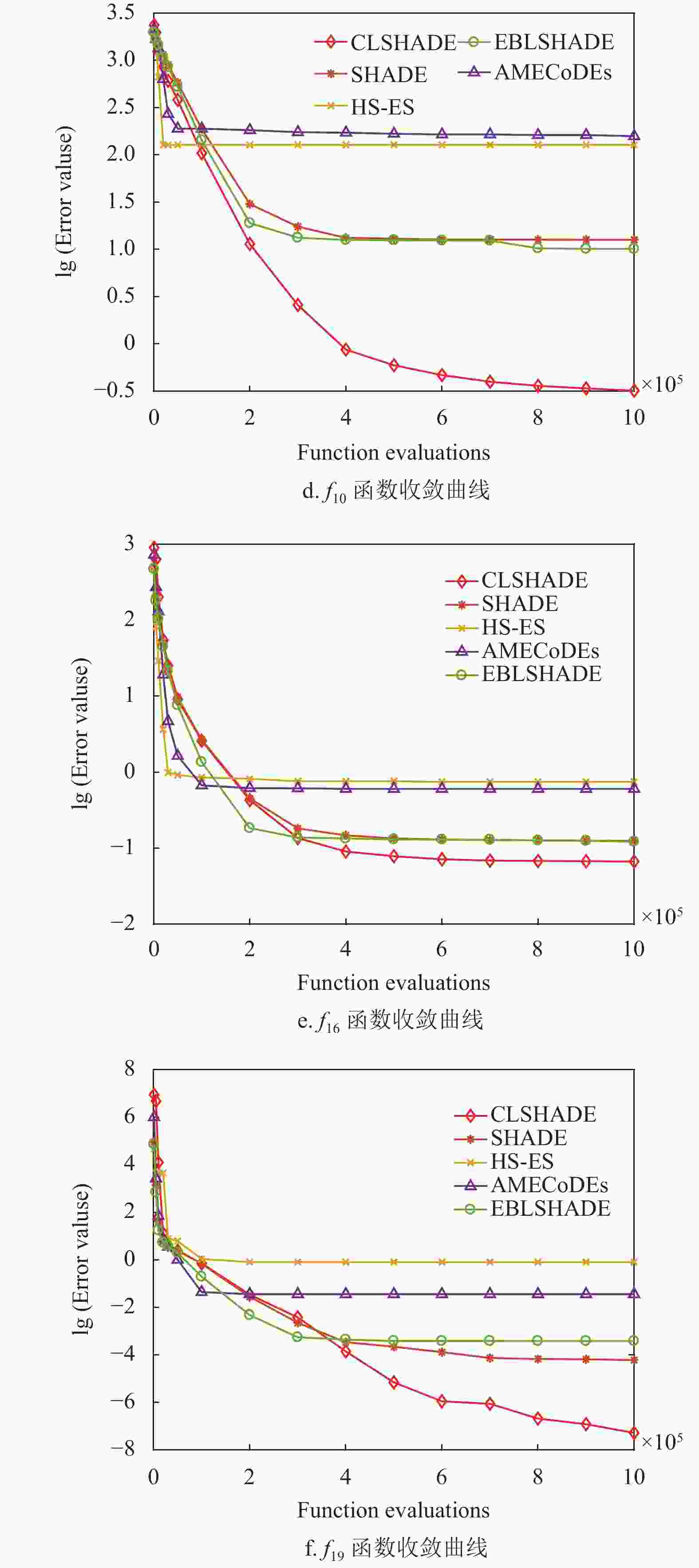
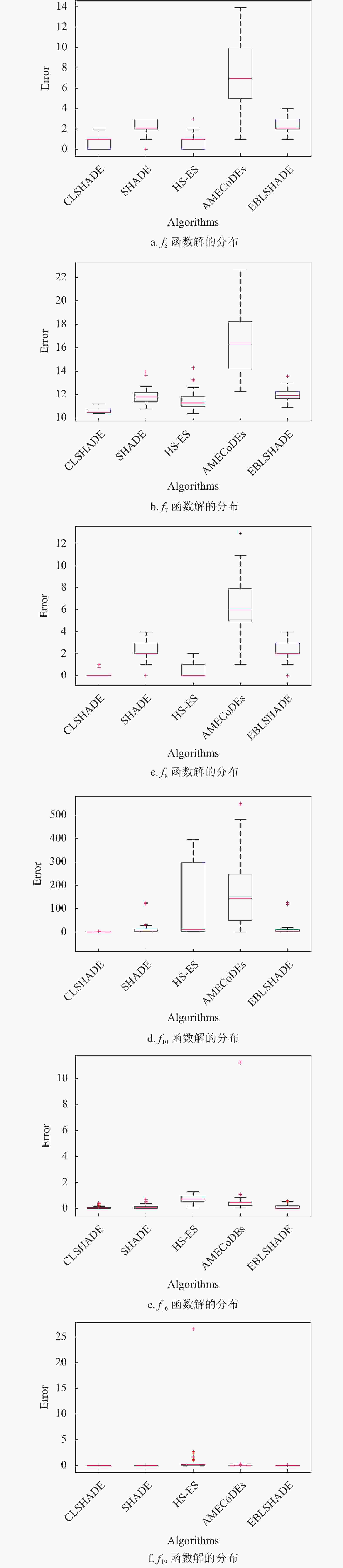
图4列出了部分函数的收敛图，可以看出CLSHADE算法与其他算法在进化前期与其他算法收敛速度接近。但是随着进化迭代次数的增加，构造的$ {{\boldsymbol{X}}}_{{\rm{cpbest}}}^t $更接近最优解所在的区域，其引导搜索的作用更加明显，因此算法执行后期收敛速度加快并且解的精度也有明显的提升，如图中函数${f_8}$、${f_{10}}$、${f_{16}}$及${f_{19}}$等所示。

图5反映了与图4对应函数各算法最优解的分布情况，可以看出CLSHADE算法在函数${f_7}$、${f_8}$和${f_{10}}$上具有良好的分布特性，表现优秀；在函数${f_5}$、${f_{16}}$和${f_{19}}$上与其他优秀算法表现相当，解的分布都比较集中，具有良好的稳定性。

表6为CLSHADE与其他算法在显著性水平为0.05和0.1下的Wilcoxon非参数检验结果，可以看出在所有10维问题上CLSHADE与其他算法存在显著差异，都优于其他对比算法。在30维问题上，CLSHADE显著优于SHADE和AMECoDEs，当显著水平为0.1时优于HS-ES算法，其他情况下虽然不存在显著性差异，但从$R - $值明显大于$R + $也可以得出CLSHADE优于其他算法。因此，从统计学的角度来说，CLSHADE总体表现优于其他对比算法。

本文提出了一种基于构造学习的差分进化算法求解变量部分可分函数优化问题，采用差分分组技术揭示决策变量的底层交互结构和形成子成分并进行解耦分组；通过构造学习策略利用问题潜在的结构知识构造最优解并向其学习提升算法的寻优性能。在CEC 2017部分可分测试函数上的实验结果表明，本文算法在解的精度、收敛性和稳定性等方面均表现突出。