-
Quantum entanglement is widely used in quantum communication, such as quantum key distribution[1-3], quantum superdense coding[4], quantum secure direct communication[5-7], and quantum teleportation[8-12]. The transmission of quantum state could be implemented by quantum teleportation (QT) with the large information capacity and high reliability, but could not be accomplished by pure complete classical methods or pure quantum methods.
In 1993, Ref. [8] firstly presented a complete QT scheme to transfer an arbitrary unknown single-particle to a distant receiver from a sender by using maximally entangled Bell states. Ref. [13] extended the discrete variable teleportation theory of Ref. [8] and conceptually defined the teleportation of continuous variables in 1994. Ref. [14] successfully achieved the single-particle quantum teleportation experimentally in 1997. In 1998, Ref. [15], based on Ref. [11], realized the teleportation of the continuous coherent light field by using the two-mode squeezed vacuum field. With the development of technology, the transmitted particles have expanded from the initial single-particle state[16-17] to the multi-particle state[18-19], and the teleportation channels have also expanded from the initial two-particle state to the multi-particle state[20], which composed of the W state, GHZ state, or some other combination of states.
In a practical situation, the influence of the environment and the inevitable occurrence of decoherence make it impossible for entangled channels to be in an ideal, noiseless, and maximally entangled state. Evenmore, they may be in non-maximally entangled states or even mixed states. If these quantum channels are not in maximally entangled state, it is impossible to transmit particles with perfect probability and fidelity. However, it has been shown that QT with the perfect fidelity can also be achieved by using non-maximally entangled states but with a probability less than 1, so it turns out to be possible to use the non-maximally entangled basis as the measurement basis. This new idea of QT is called probabilistic quantum teleportation (PQT)[21-22].
Subsequently, QT has been further developed, and the QT scheme has also been generalized to the controlled quantum teleportation (CQT)[23] and
$ N $ particles QT[24] by using various kinds of quantum channels and the design of the process. There are many CQT schemes[25-26], such as some special bidirectional controllable quantum teleportation (BCQT)[27-29] and cyclic controllable quantum teleportation (CCQT)[30-32].We propose two controllable probabilistic teleportation schemes for an arbitrary three-particle GHZ state or W state in this paper, by using a partially entangled four-particle state and a partially entangled three-particle state as the QT channel. At the same time, our schemes can implement teleportation from a sender to either one of the two receivers. To recover the unknown state, apart from the sender, the only requirement for the controller is to perform Bell-state measurement, and the receiver merely needs to have the ability to perform the unitary operation with the help of the controller. The overall success probabilities of our two schemes are both
$ 8d^2n^2 $ . The probability of success can attain 100$ \% $ if the channel is in its maximally entangled state. -
We first introduce the process of realizing teleportaion of the three-particle unknown GHZ state. Suppose Alice is the sender and the two possible receivers are Bob and Charlie. If Bob is the receiver, then Charlie is the controller, and vice versa. The arbitrary GHZ state to be teleported is denoted by:
where the unknown numbers
$ x $ and$ y $ meet$ {\lvert x\rvert}^2+{\lvert y\rvert}^2 = 1 $ . A four-particle partially entangled state and a three-particle partially entangled state constitute the channel we need for teleportation. To ensure generality, the quantum channel linking Alice, Bob, and Charlie can be written as follows:where
$ a $ ,$ b $ ,$ c $ ,$ d $ ,$ m $ ,$ n $ are real coefficients and satisfy$ {\lvert a\rvert}^2+{\lvert b\rvert}^2+{\lvert c\rvert}^2+{\lvert d\rvert}^2 = 1 $ ,$ {\lvert m\rvert}^2+{\lvert n\rvert}^2 = 1 $ and$ \lvert a\rvert>\lvert b\rvert> \lvert c\rvert>\lvert d\rvert $ ,$ \lvert m\rvert>\lvert n\rvert $ . The definition of Bell states$ \vert\varPsi^\pm\rangle_{ij} $ and$ \vert\varPhi^\pm\rangle_{ij} $ are given as following:The above four-particle and three-particle partially entangled states are shared by two possible receivers (Bob and Charlie) and the sender (Alice) that are sufficiently far apart in space. Assume that the sender Alice has particles 1, 5,
$ A $ ,$ B $ , and$ C $ , Bob has particles 4,7, the remaining two particles 3 and 6, belong to Charlie. Initially, the state of the three-particle unknown GHZ state and the channel composed of four-particle and three-particle partially entangled state is given by:In our quantum teleportation scheme, there are the following three steps.
1) In order to achieve teleportation, the first step Alice has to do is to carry out Bell-state measurement on particle pair (
$ A $ ,1) and particle pair ($ B $ ,5) in turn. After the measurement is completed, the following different quantum states will be generated according to the different measurement basis:where
$ \pm^1,\pm^2 $ represent the results corresponding to the measurement outcomes of the Bell-state on particle pairs ($ A $ ,1) and ($ B $ ,5), respectively.2) Alice performs a single-particle measurement on particle C, where the measurement basis is
$ \vert\xi^\pm\rangle = \dfrac{1}{\sqrt2}(\vert0\rangle\pm\vert1\rangle) $ . After the measurement is completed, Eqs. (7)~Eqs. (10) can be rewritten as the following four equations:where
$ \pm^3 $ denotes measurement result on particle C.3) Now, notice that the attribution of particle 2 depends on the person who wants to restore the state
$ \vert\eta\rangle_{ABC} $ , here we assume that Bob wants to restore the state$ \vert\eta\rangle_{ABC} $ , then Charlie is the controller. Alice has to transmit the measurements result to Bob and Charlie over the classical channel after she has completed the measurement, and Charlie needs to perform a Bell-state measurement on particles (3,6) at the request of Bob. After the measurement is completed, Eqs. (11)~Eqs. (14) can be rewritten as the following eight equations:where
$ \pm^4 $ denotes Bell-state measurement outcomes corresponding to particles (3,6).4) After the measurement, according to the different measurement results delivered by Charlie through the classical channel, Bob can choose the appropriate unitary operation to restore the unknown state
$ \vert\eta\rangle_{ABC} $ . Then Bob needs to construct a corresponding relationship between$ \vert000\rangle_{247},\vert111\rangle_{247} $ and the coefficients$ x $ and$ y $ , respectively. For instance, assume that the measurement results of Alice are$\vert\varPhi^+\rangle_{A1}\vert\varPhi^+\rangle_{B5}\vert\xi^+\rangle_{C}$ , the measurement result of Charles is$\vert\varPhi^+\rangle_{36}$ , so when Charlie tells Bob the measurement result on particle pair (3,6), Bob can infer that the quantum state collapses into$ \dfrac{1}{4}(xbm\vert101\rangle+ycn\vert010\rangle)_{247} $ . To recover the initial state, Bob ought to implement the Pauli$ {\boldsymbol{X}} $ operator(expressed as$ {\boldsymbol{X}} $ ) on particle 5,7 and perform the identity operator (expressed as$ {\boldsymbol{I}} $ ) on particle 6. That is,$ {\boldsymbol{U}}_1 = {\boldsymbol{X}}_5\bigotimes {\boldsymbol{I}}_6\bigotimes {\boldsymbol{X}}_7 $ . Therefore, Bob will obtain:5) Bob adds an auxiliary particle
$ H $ where$ \vert0\rangle_H $ is as its original state. Then he performs an unitary matrix$ {\boldsymbol{U}}_2 $ based on a set of basis$ \{\vert00\rangle_{7H},\vert01\rangle_{7H}, \vert10\rangle_{7H},\vert11\rangle_{7H}\} $ :where
$ {\boldsymbol{H}}_i $ ($ i = 1,2 $ ) is a 2$ \times $ 2 matrix, they can be written as$ {\boldsymbol{H}}_1 $ = diag($ h_0 $ ,$ h_1 $ ),$ {\boldsymbol{H}}_2 $ = diag($ \sqrt{1-h_0^2} $ ,$ \sqrt{1-h_1^2} $ ), and ($ h_0 $ ,$ h_1 $ ) = ($ \dfrac{dn}{bm} $ ,$ \dfrac{d}{c} $ ). Under this transformation, the state in Eq.(23) will transform into:6) Finally, Bob needs to measure particle
$ H $ . The measurement result of$ \vert0\rangle_H $ means that the teleportation of their joint efforts is successful and the measurement result of$ \vert1\rangle_H $ means failure.In the process, Bob must carry out different unitary operations according to the state that he has got. Table 1 shows all possible states obtained by Bob and the corresponding unitary operation
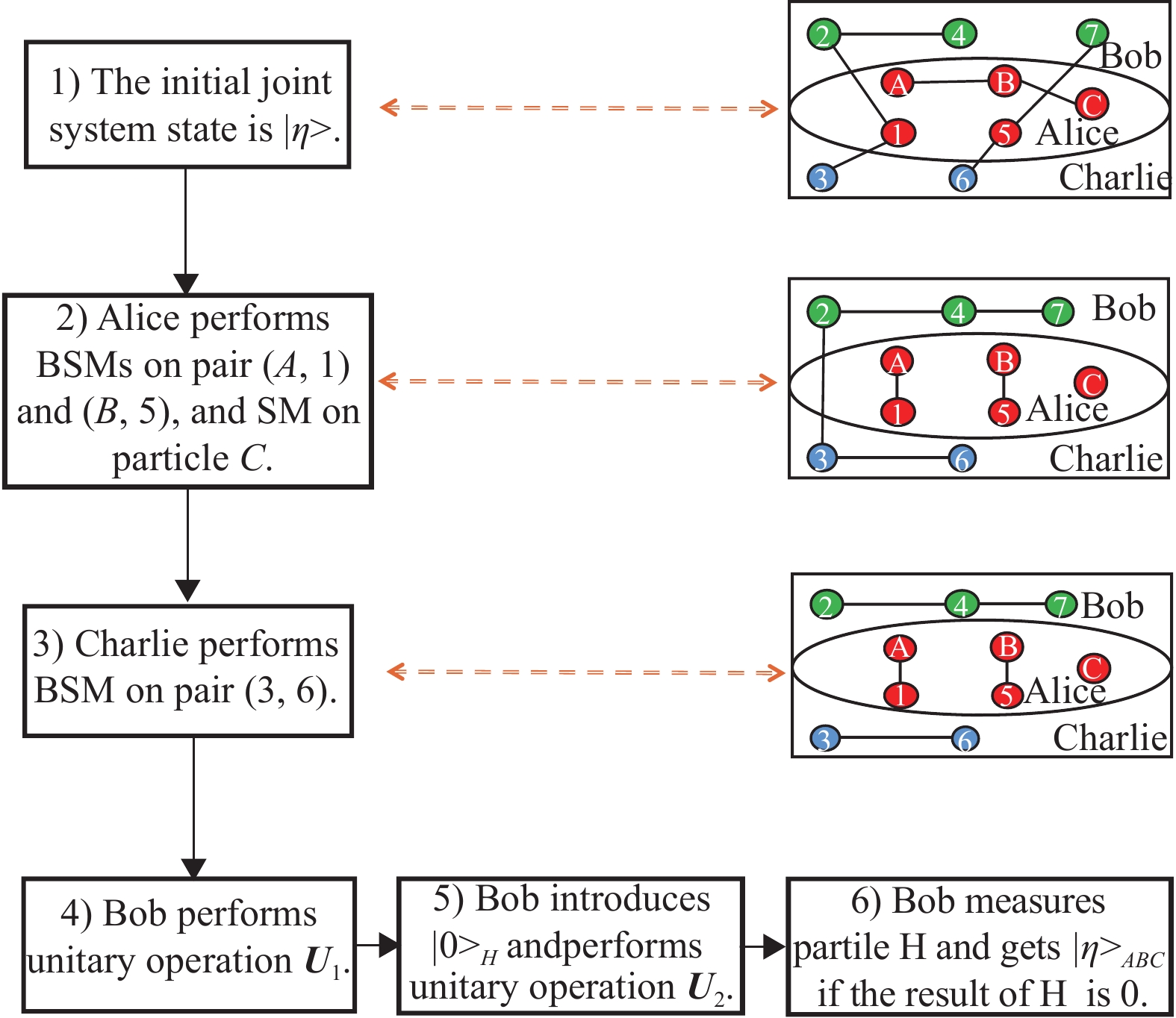
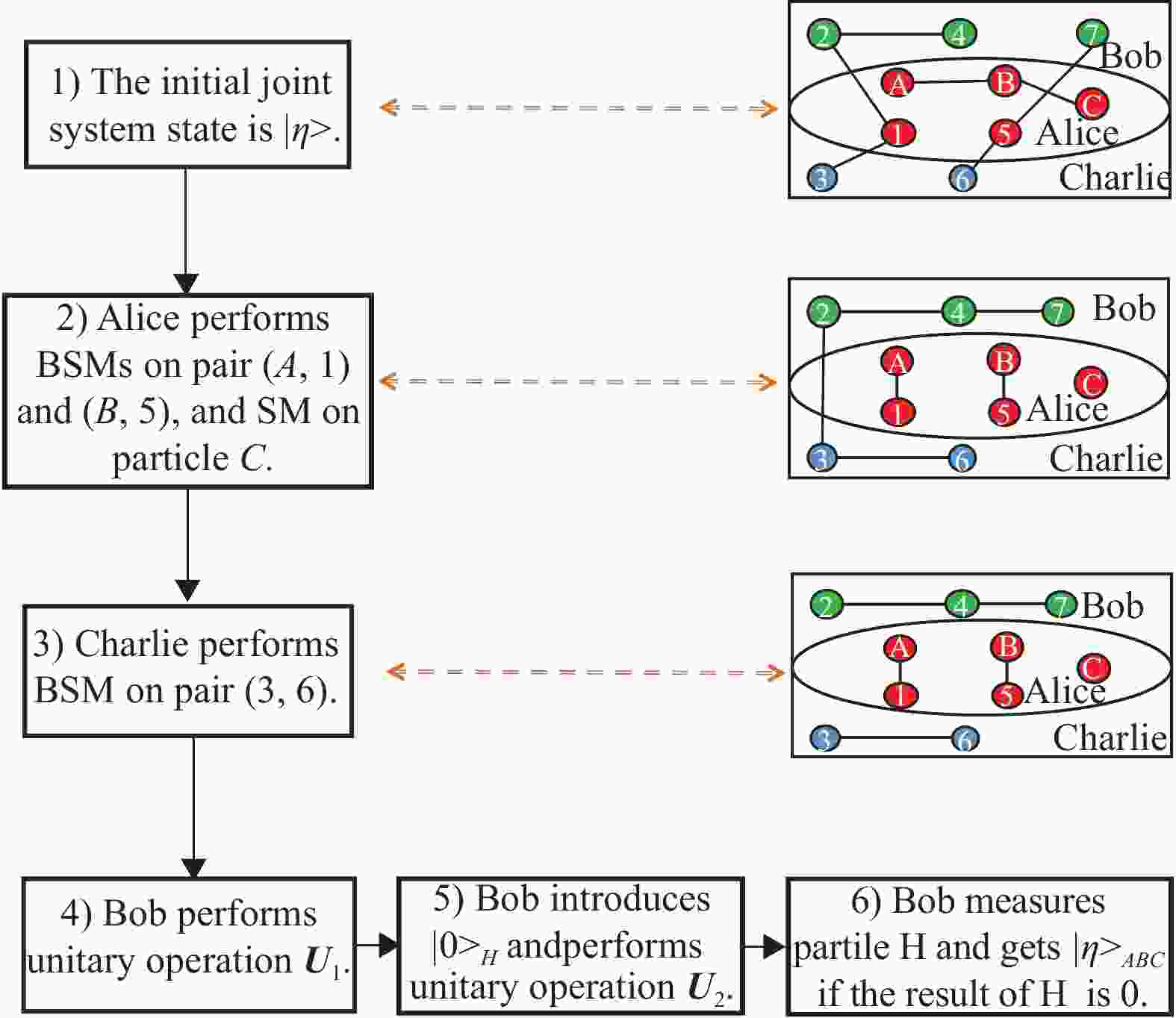
$ {\boldsymbol{U}}_1 $ . Table 2 shows the values of different$ h_i $ in unitary operation$ {\boldsymbol{U}}_2 $ .The main process of our PQT scheme, in which Bob is as the receiver, is illustrated as Fig. 1. The particles are represented by solid circles and the entanglement between particles is represented by solid lines. The drawings on the rightside are entanglement representation in steps 1), 2), 3), respectively. BSM and SM are as Bell-state measurement and single-particle measurement.
Bob’s states Bob’s operation $xbm\vert101\rangle+ycn\vert010\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{X}}_7$ $xbm\vert101\rangle-ycn\vert010\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{I}}_6\otimes (i{\boldsymbol{Y}})_7$ $-xbm\vert101\rangle+ycn\vert010\rangle$ $(-i{\boldsymbol{Y}})_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{X}}_7$ $-xbm\vert101\rangle-ycn\vert010\rangle$ $(-{\boldsymbol{X}})_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{X}}_7$ $xam\vert111\rangle+ydn\vert000\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{X}}_6\otimes {\boldsymbol{X}}_7$ $xam\vert111\rangle-ydn\vert000\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{X}}_6\otimes (i{\boldsymbol{Y}})_7$ $xan\vert110\rangle+ydm\vert001\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{X}}_6\otimes {\boldsymbol{I}}_7$ $xan\vert110\rangle-ydm\vert001\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{X}}_6\otimes {\boldsymbol{Z}}_7$ $xbn\vert100\rangle+ycm\vert011\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{I}}_7$ $xbn\vert100\rangle-ycm\vert011\rangle$ ${\boldsymbol{X}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{Z}}_7$ $-xbn\vert100\rangle+ycm\vert011\rangle$ $(-i{\boldsymbol{Y}})_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{I}}_7$ $-xbn\vert100\rangle-ycm\vert011\rangle$ $(-{\boldsymbol{X}})_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{I}}_7$ $xdm\vert001\rangle+yan\vert110\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{X}}_7$ $xdm\vert001\rangle-yan\vert110\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes (i{\boldsymbol{Y}})_7$ $-xdm\vert001\rangle+yan\vert110\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes (-i{\boldsymbol{Y}})_7$ $-xdm\vert001\rangle-yan\vert110\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes (-{\boldsymbol{X}})_7$ $xcm\vert011\rangle+ybn\vert100\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{X}}_6\otimes {\boldsymbol{X}}_7$ $xcm\vert011\rangle-ybn\vert100\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{X}}_6\otimes (i{\boldsymbol{Y}})_7$ $xcn\vert010\rangle+ybm\vert101\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{X}}_6\otimes {\boldsymbol{I}}_7$ $xcn\vert010\rangle-ybm\vert101\rangle$ ${\boldsymbol{I}}_5\otimes (i{\boldsymbol{Y}})_6\otimes {\boldsymbol{I}}_7$ $xdn\vert000\rangle+yam\vert111\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{I}}_7$ $xdn\vert000\rangle-yam\vert111\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes {\boldsymbol{Z}}_7$ $-xdn\vert000\rangle+yam\vert111\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes (-{\boldsymbol{Z}})_7$ $-xdn\vert000\rangle-yam\vert111\rangle$ ${\boldsymbol{I}}_5\otimes {\boldsymbol{I}}_6\otimes (-{\boldsymbol{I}})_7$ Table 1. States and the corresponding unitary operation
${\boldsymbol{U}}_1$ for Bobrestored state by ${\boldsymbol{U}}_1$ $h_0$ $h_1$ $xbm\vert000\rangle+ycn\vert111\rangle$ $\dfrac{dn}{bm}$ $\dfrac{d}{c}$ $xam\vert000\rangle+ydn\vert111\rangle$ $\dfrac{dn}{am}$ 1 $xan\vert000\rangle+ydm\vert111\rangle$ $\dfrac{d}{a}$ $\dfrac{n}{m}$ $xbn\vert000\rangle+ycm\vert111\rangle$ $\dfrac{d}{b}$ $\dfrac{dn}{cm}$ $xdm\vert000\rangle+yan\vert111\rangle$ $\dfrac{n}{m}$ $\dfrac{d}{a}$ $xcm\vert000\rangle+ybn\vert111\rangle$ $\dfrac{dn}{cm}$ $\dfrac{d}{b}$ $xcn\vert000\rangle+ybm\vert111\rangle$ $\dfrac{d}{c}$ $\dfrac{dn}{bm}$ $xdn\vert000\rangle+yam\vert111\rangle$ 1 $\dfrac{dn}{am}$ Table 2.
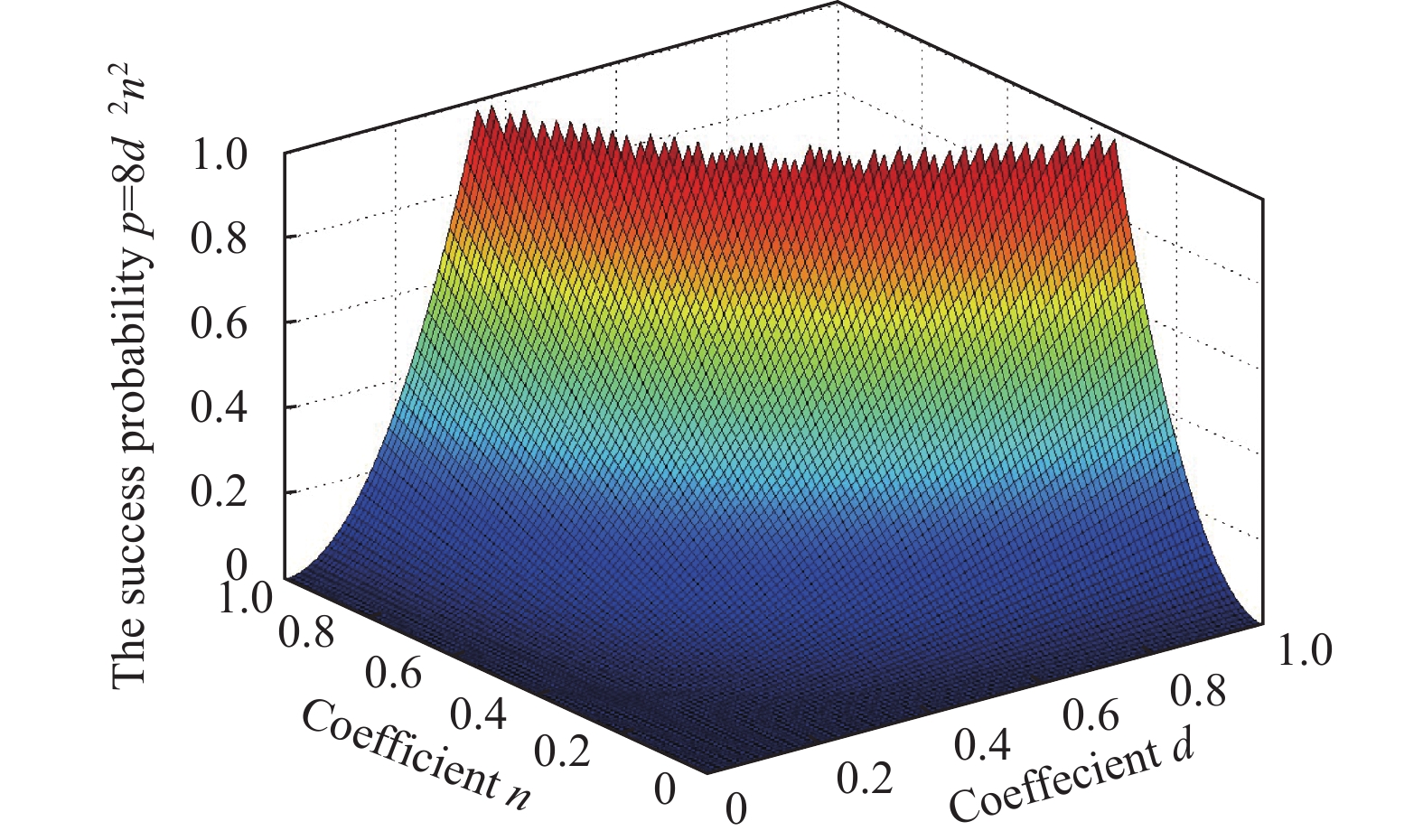
$h_i$ in the unitary operation${\boldsymbol{U}}_2$ In the former case, the state of particles 2,4,7 will collapse into
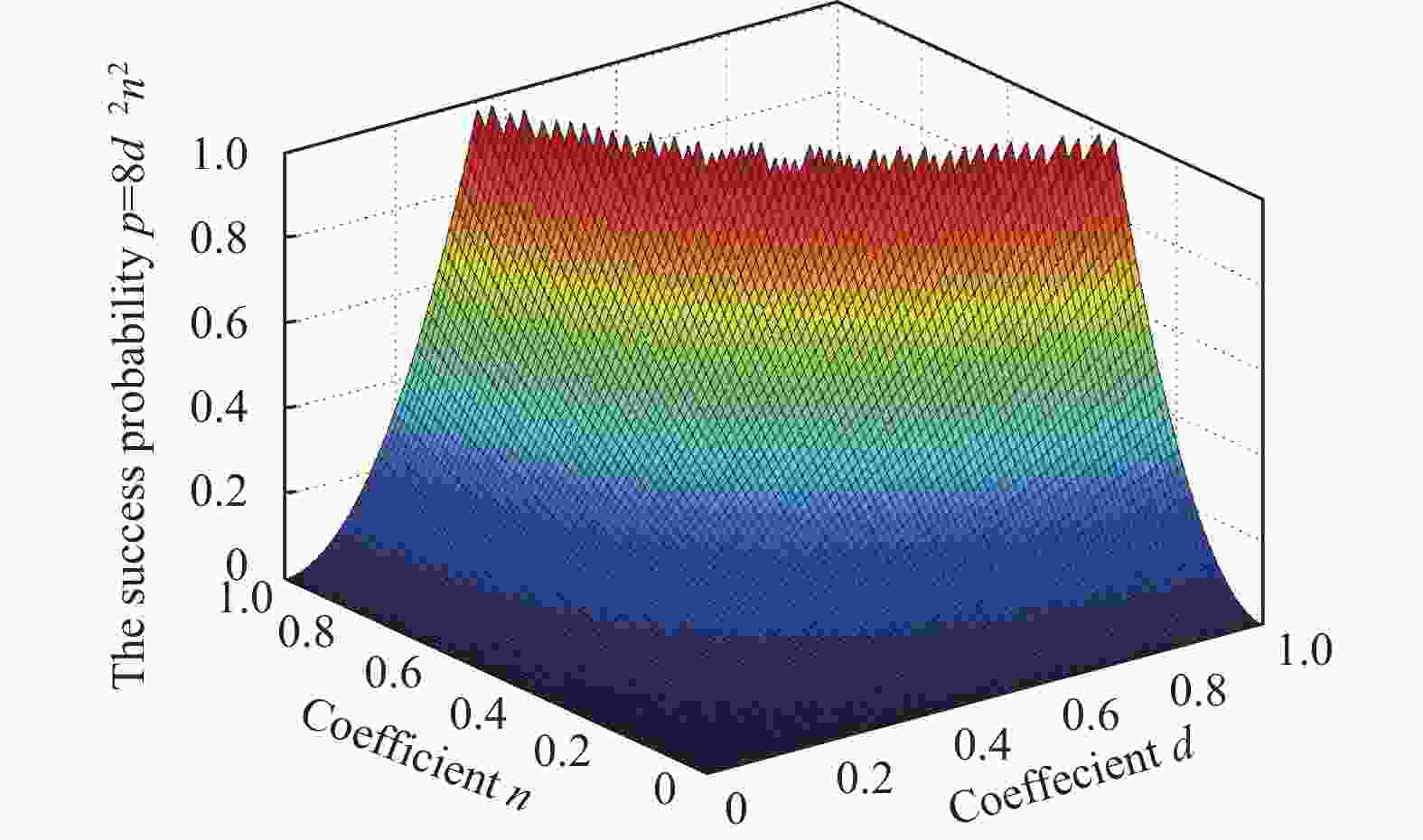
$ \dfrac{1}{4}dn(x\vert000\rangle+y\vert111\rangle)_{247} $ , and the probability of success is$ \dfrac{1}{16}d^2n^2 $ . Simultaneously, for Eq. (15), since Alice and Charlie have two different choices for each measurement, there are 16 possible cases in total. It’s easy to figure out that the probability of success is$ d^2n^2 $ . Considering that there are 128 cases, the total success probability is$ 8d^2n^2 $ . We show the success probability surface of our PQT in Fig. 2, which gives the relationship between probability and coeffecients$ d $ and$ n $ .If the coefficients in Eq. (2) satisfy
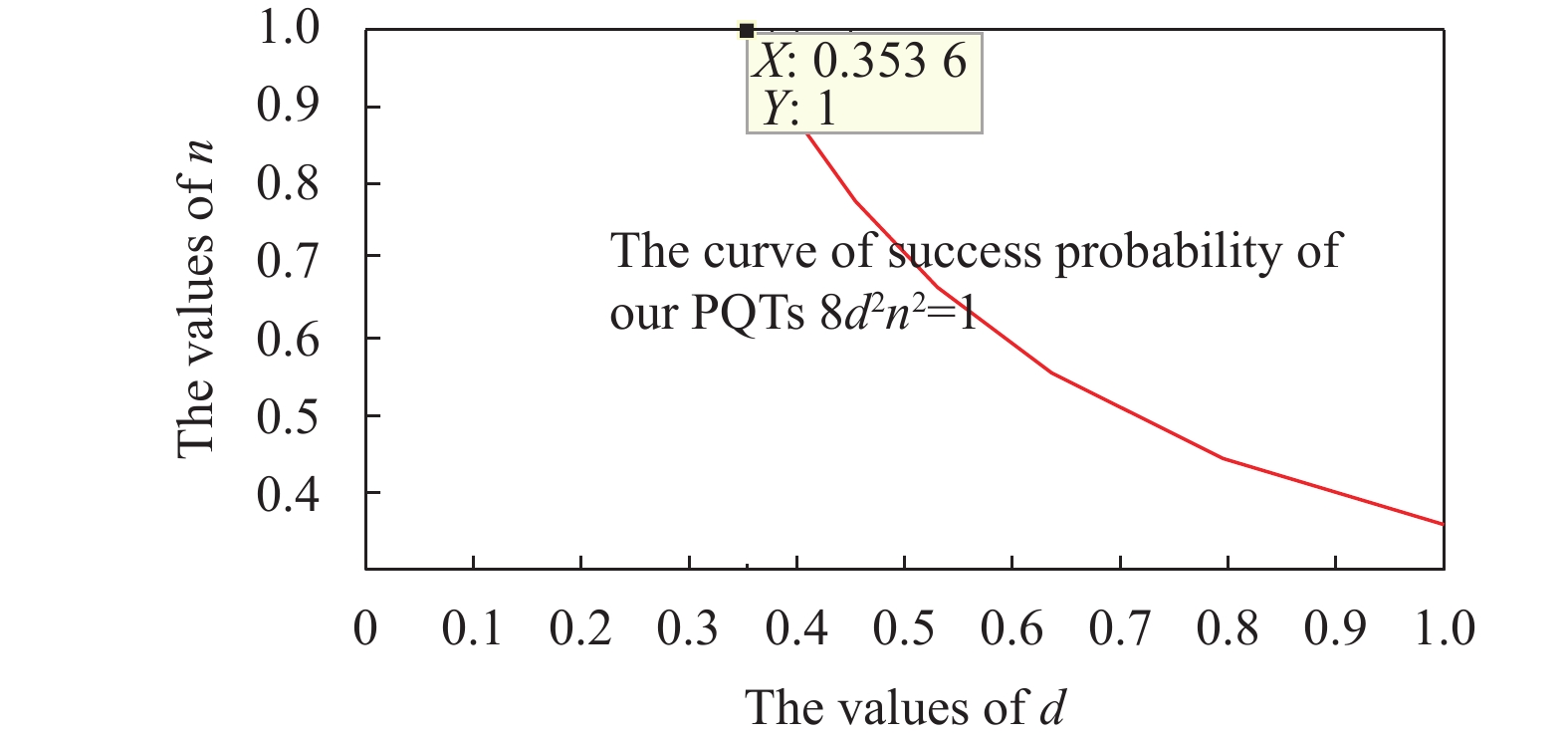
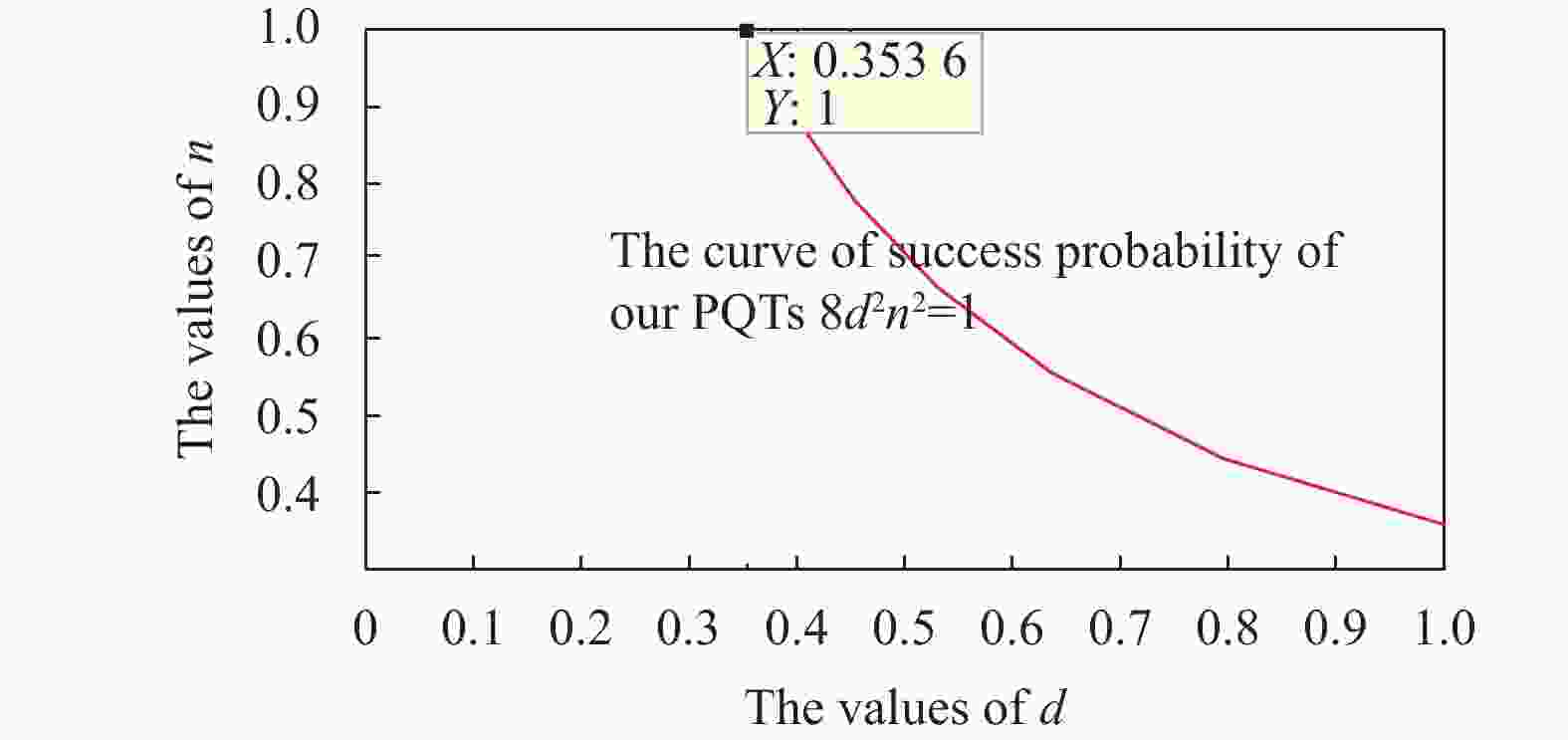
$ a = b = c = d = \dfrac{1}{2} $ and the coefficients in Eq. (3) satisfy$ m = n = \dfrac{1}{\sqrt{2}} $ , then the channel will be in its maximally entangled states, and thus the probability of teleportation equals 1. Namely, this is the usual teleportation. Fig. 3 illustrates the relation between$ d $ and$ n $ when the probability$ 8d^2n^2 = 1 $ .Likewise, if the person who wants to restore the state
$ \vert\eta\rangle_{ABC} $ is Charlie, then assign particle 2 to him. First of all, after Alice makes her measurements on particles (A,1), (B,5), and C, she sends the measurement result to Charlie through the classical channel. Next, Bob needs to carry out a Bell-state measurement on particles (4,7) at the request of Charlie. The remaining steps are the same as the case when the person who wants to restore the state$ \vert\eta\rangle_{ABC} $ is Bob. It is not difficult to figure out the probability that Charlie can recover the initial state$ \vert\eta\rangle_{ABC} $ is$ 8d^2n^2 $ . Accordingly, we can find that whether the person who wants to restore the original state is Bob or Charlie, the probability of success is the same in both cases. -
Assuming that the state we want to transmit is not the GHZ state but the three-particle W state, through the following discussion we can find that the quantum channel we constructed in Eqs. (2) and Eqs. (3) can also realize the teleportation of arbitrary three-particle W states. The arbitrary W state to be teleported can be written as:
where the unknown real numbers
$ p,q,r $ satisfy$ {\lvert p\rvert}^2+{\lvert q\rvert}^2+{\lvert r\rvert}^2 = 1 $ .If Alice is the sender, she intends to transmit a three-particle W state, and Charlie, who is far away from Alice, wants to get this state with the help of Bob (Here, for simplicity, we only consider the cases where Charlie is the receiver). Assume that Alice has particles 1,5,
$ A $ ,$ B $ , and$ C $ , Charlie has particles 2,4,7 and the remaining two particles 3,6 belong to the controller Bob. Initially, the state of the composite system is given by:To achieve teleportation from Alice to Charlie, the first step Alice needs to do is to operate Bell-state measurement on particle pairs (
$ A' $ ,1) and ($ B' $ ,5) in possession, respectively. Next, Alice needs to perform single-particle measurement on particle C, where the measurement basis is$ \vert\xi^\pm\rangle = \dfrac{1}{\sqrt2}(\vert0\rangle\pm\vert1\rangle) $ . After operations, Alice needs to send the measurement result to Bob and Charlie through the classical channel. If Bob is willing to help Charlie to rebuild the initial state, Bob has to carry out Bell-state measurement on particle pair (3,6). In the light of the result of Alice and Bob, Charlie will be able to rebuild the original state in Eq. (25) by performing a suitable unitary operation$ {\boldsymbol{U}}_1' $ on the particles 2,4,7. We show all possible states obtained by Charlie and the corresponding unitary operation$ {\boldsymbol{U}}_1' $ in Table 3.Charlie’s states Charlie’s operation $\pm^4\pm^3pbm\vert101\rangle\pm^2qan\vert110\rangle\pm^4\pm^1rdm\vert001\rangle$ $\vert000\rangle\langle000\vert+\vert110\rangle\langle010\vert+\vert101\rangle\langle100\vert\pm^2\vert010\rangle\langle110\vert\pm^4\pm^1$ $\vert100\rangle\langle001\vert+\vert011\rangle\langle011\vert\pm^4\pm^3\vert001\rangle\langle101\vert+\vert111\rangle\langle111\vert$ $\pm^3pam\vert111\rangle\pm^4\pm^2qbn\vert100\rangle\pm^1rcm\vert011\rangle$ $\vert000\rangle\langle000\vert+\vert011\rangle\langle010\vert\pm^4\pm^2\vert010\rangle\langle100\vert+\vert110\rangle\langle110\vert+$ $ \vert101\rangle\langle001\vert\pm^1\vert100\rangle\langle011\vert+\vert111\rangle\langle101\vert\pm^3\vert001\rangle\langle111\vert$ $\pm^3pan\vert110\rangle\pm^4\pm^2qbm\vert101\rangle\pm^1rcn\vert010\rangle$ $\vert000\rangle\langle000\vert\pm^1\vert100\rangle\langle010\vert+\vert110\rangle\langle100\vert\pm^3\vert001\rangle\langle110\vert+$ $ \vert101\rangle\langle001\vert+\vert011\rangle\langle011\vert\pm^4\pm^2\vert010\rangle\langle101\vert+\vert111\rangle\langle111\vert$ $\pm^4\pm^3pbn\vert100\rangle\pm^2qam\vert111\rangle\pm^4\pm^1rdn\vert000\rangle$ $\vert000\rangle\langle001\vert+\vert011\rangle\langle011\vert+\vert101\rangle\langle101\vert\pm^2\vert010\rangle\langle111\vert$$\pm^4\pm^1$ $ \vert100\rangle\langle000\vert+\vert110\rangle\langle010\vert\pm^4\pm^3\vert001\rangle\langle100\vert+\vert111\rangle\langle110\vert $ $\pm^4\pm^3pdm\vert001\rangle\pm^2qcn\vert010\rangle\pm^4\pm^1rbm\vert101\rangle$ $\vert000\rangle\langle000\vert\pm^2\vert010\rangle\langle010\vert+\vert101\rangle\langle100\vert+\vert110\rangle\langle110\vert\pm^4\pm^3$ $ \vert001\rangle\langle001\vert+\vert011\rangle\langle011\vert\pm^4\pm^1\vert100\rangle\langle101\vert+\vert111\rangle\langle111\vert$ $\pm^3pcm\vert011\rangle\pm^4\pm^2qdn\vert000\rangle\pm^1ram\vert111\rangle$ $\vert001\rangle\langle010\vert\pm^4\pm^2\vert010\rangle\langle000\vert+\vert000\rangle\langle100\vert+\vert110\rangle\langle110\vert+$ $ \vert111\rangle\langle001\vert\pm^3\vert011\rangle\langle011\vert+\vert101\rangle\langle101\vert\pm^1\vert100\rangle\langle111\vert$ $\pm^3pcn\vert010\rangle\pm^4\pm^2qdm\vert001\rangle\pm^1ran\vert110\rangle$ $\vert011\rangle\langle011\vert\pm^4\pm^2\vert010\rangle\langle001\vert+\vert101\rangle\langle101\vert+\vert111\rangle\langle111\vert+$ $\vert000\rangle\langle000\vert\pm^3\vert001\rangle\langle010\vert+\vert110\rangle\langle100\vert\pm^1\vert100\rangle\langle110\vert $ $\pm^4\pm^3pdn\vert000\rangle\pm^2qcm\vert011\rangle\pm^4\pm^1rbn\vert100\rangle$ $\vert000\rangle\langle001\vert\pm^2\vert010\rangle\langle011\vert+\vert101\rangle\langle101\vert+\vert111\rangle\langle111\vert\pm^4\pm^3$ $\vert001\rangle\langle000\vert+\vert011\rangle\langle010\vert\pm^4\pm^1\vert100\rangle\langle100\vert+\vert110\rangle\langle110\vert $ Table 3. Unitary operations
${\boldsymbol{U}}_1'$ corresponding to the state obtained by CharlieSimilarly, Charlie needs to add an auxiliary particle
$ {{H}} $ ,$ \vert0\rangle_H $ is its original state. Then Charlie performs unitary matrix$ {\boldsymbol{U}}_2' $ based on a set of basis$ \{\vert000\rangle_{47H},\vert100\rangle_{47H},\vert010\rangle_{47H},\vert001\rangle_{47H},\vert101\rangle_{47H}, $ $ \vert011\rangle_{47H}\} $ :where
$ {\boldsymbol{H}}_i' $ ($ i $ = 1,2) is a 3×3 matrix, written as$ {\boldsymbol{H}}_1' $ = diag($ h_0 $ ,$ h_1 $ ,$ h_2 $ ),$ {\boldsymbol{H}}_2' $ = diag($ \sqrt{1-h_0^2} $ ,$ \sqrt{1-h_1^2} $ ,$ \sqrt{1-h_2^2} $ ). The values of$ h_i $ in the unitary operations$ {\boldsymbol{U}}_2' $ are shown in Table 4.Since the measurement process is the same as Section 1, we only give the collapse state of particles (2,4,7) after measurement.
restored state by ${\boldsymbol{U}}_1'$ $h_0$ $h_1$ $h_2$ $pbm\vert001\rangle+qan\vert010\rangle+rdm\vert100\rangle$ $\dfrac{n}{m}$ $\dfrac{d}{a}$ $\dfrac{dn}{bm}$ $pam\vert001\rangle+qbn\vert010\rangle+rcm\vert100\rangle$ $\dfrac{dn}{cm}$ $\dfrac{d}{b}$ $\dfrac{dn}{am}$ $pan\vert001\rangle+qbm\vert010\rangle+rcn\vert100\rangle$ $\dfrac{d}{c}$ $\dfrac{dn}{bm}$ $\dfrac{d}{a}$ $pbn\vert001\rangle+qam\vert010\rangle+rdn\vert100\rangle$ 1 $\dfrac{dn}{am}$ $\dfrac{d}{b}$ $pdm\vert001\rangle+qcn\vert010\rangle+rbm\vert100\rangle$ $\dfrac{dn}{bm}$ $\dfrac{d}{c}$ $\dfrac{n}{m}$ $pcm\vert001\rangle+qdn\vert010\rangle+ram\vert100\rangle$ $\dfrac{dn}{am}$ 1 $\dfrac{dn}{cm}$ $pcn\vert001\rangle+qdm\vert010\rangle+ran\vert100\rangle$ $\dfrac{d}{a}$ $\dfrac{n}{m}$ $\dfrac{d}{c}$ $pdn\vert001\rangle+qcm\vert010\rangle+rbn\vert100\rangle$ $\dfrac{d}{b}$ $\dfrac{dn}{cm}$ 1 Table 4.
$h_i$ in the unitary operations${\boldsymbol{U}}_2'$ Now we take
$ \vert\varPhi^+\rangle_{A1}\vert\varPhi^+\rangle_{B5}\vert\xi^+\rangle_{C}\vert\varPhi^+\rangle_{36} $ as an example to show how to achieve teleportation. Suppose that:In order to recover the initial state
$ \vert\eta'\rangle_{A'B'C'} $ , Charlie has to carry out an appropriate unitary operation:Then, Charlie will obtain:
Next, we set
$ h_0 = \dfrac{n}{m} $ ,$ h_1 = \dfrac{d}{a} $ ,$ h_2 = \dfrac{dn}{bm} $ in the unitary matrix$ {\boldsymbol{U}}_2' $ . Through a unitary transformation similar to$ {\boldsymbol{U}}_2 $ , the state in Eq. (27) will transform into:Finally, Charlie needs to measure particle H. The measurement result of
$ \vert0\rangle_H $ means the teleportation of their joint efforts is successful, and the measurement result of$ \vert1\rangle_H $ means failure. In the former case, the state of particles 2,4 and 7 will collapse into$ \dfrac{1}{4}dn(p\vert001\rangle+q\vert010\rangle+r\vert100\rangle)_{247} $ , and the probability of success is$ \dfrac{1}{16}d^2n^2 $ . Similarly, other possible states can be calculated in the same way. Therefore, the total probability of success is$ 8d^2n^2 $ based on all 128 cases. If the coefficients in Eq. (2) satisfy$ a = b = c = d = \dfrac{1}{2} $ and the coefficients in Eq. (3) satisfy$ m = n = \dfrac{1}{\sqrt{2}} $ , then the channel will be in its maximally entangled state, and the probability of teleportation equals 1. -
In summary, two explicit tripartite schemes are proposed for the controllable probabilistic teleportation of any unknown partially entangled GHZ or W state. At the same time, our schemes can implement teleportation from the sender to either one of the two receivers. In these two schemes, we construct a new quantum channel which is consisted of a one-dimensional four-particle partially entangled state and a three-particle partially entangled state. This channel can realize not only the transmission of the GHZ state but also the transmission of the W state. The processes of our schemes are the sender carries out two Bell-state measurement and a single-particle measurement on suitable particles, the controller performs a Bell-state measurement, the receiver performs the corresponding unitary operation and introduces an auxiliary particle. After these processes are completed, the unknown state can be transmitted with a certain probability, depending on the coefficient with the smallest absolute value in the four-particle partially entangled state and the coefficient with the smallest absolute value in the three-particle partially entangled state.
Since devices cannot be perfect in the experiment, the generation of maximally entangled state is not possible. Entanglement purification methods are usually helpful for acquiring the ideal entangled state but often requires additional resources. Accordingly, our schemes are more feasible in experiments. We can find that the overall success probabilities of the two schemes are both
$ 8d^2n^2 $ . If the channel is the maximally entangled state, then probabilistic teleportation becomes the usual teleportation, which has a probability of success equal to 100$ \% $ .
Probabilistic Teleportation of Arbitrary Three-Particle GHZ and W State
doi: 10.12178/1001-0548.2022356
- Received Date: 2022-10-20
- Accepted Date: 2023-04-03
- Rev Recd Date: 2023-02-23
- Available Online: 2024-04-01
- Publish Date: 2024-03-30
-
Key words:
- Bell state measurement /
- partially entangled state /
- quantum teleportation /
- unitary operation
Abstract: A new quantum channel composed of two multi-particle partially entangled states for quantum teleportation (QT) is constructed. Two explicit controlled probabilistic teleportation tripartite schemes are proposed for arbitrary three-particle partially entangled GHZ state and W state. The arbitrary GHZ state and W state can be teleported with a certain probability to the receiver who introduces an auxiliary particle and performs the corresponding unitary operation, with the help of the measurement of Bell-state and single-particle from the sender and the controller. The overall success probabilities of two QT schemes are both
| Citation: | WANG Haozhen, TAN Xiaoqing, XU Qingshan, BAO Daipengwei. Probabilistic Teleportation of Arbitrary Three-Particle GHZ and W State[J]. Journal of University of Electronic Science and Technology of China, 2024, 53(2): 291-298. doi: 10.12178/1001-0548.2022356 |

 ISSN
ISSN 











































































































































 DownLoad:
DownLoad: