2. 中北大学计算机与控制工程学院 太原 030051
2. School of Computer and Control Engineering, North University of China Taiyuan 030051
模式分类是数据挖掘、模式识别、机器学习等领域的研究热点。当前主流的分类方法可归纳为以下几类:1) 决策树。ID3算法通过互信息理论建立树状分类模型,在ID3基础上先后提出C4.5[1]、PUBLIC[2]、SLIQ[3]、RainForest[4]等改进算法;2) 关联规则算法主要包括关联分析算法[5]、多维关联规则算法以及预测性关联规则算法[6];3) 支持向量机。支持向量机(support vectorachine, SVM)[7, 8, 9, 10]起初于1995年被提出,随着应用的不断深入,根据不同的应用场合,研究人员先后提出众多改进算法:ν-SVM[11]、单类支持向量机(one class supportvector machine, OCSVM)[12]、支持向量数据描述(support vector data description,SVDD)[13] 、核心向量机(core vector machine, CVM)[14]、Lagrangian支持向量机(Largrangian support vector machine, LSVM)[15]、最小二乘支持向量机(least squares support vector machine, LSSVM)[16]以及光滑支持向量机(smooth support vector machine, SSVM)[17]等;4) 贝叶斯分类器包括半朴素贝叶斯分类器(semi-naive Bayesian classifier)、基于属性删除的选择性贝叶斯分类器(selective Bayesian classifierbased on atribute deletion)[18] 、基于懒惰式贝叶斯规则的学习算法(lazy Bayesian rule learning algorithm,LBR)[19] 及树扩张型贝叶斯分类器(tree augmented Bayesian classifier, TAN)[20]等。
上述方法在实际应用中取得良好的分类效果,但它们面临如下挑战:1) 在分类决策时无法同时考虑样本的全局特征和局部特征;2) 大多算法仅关注各类样本的可分性,而忽略样本之间的相对关系。GRPLM工作原理为,三类样本在W1方向上的投影顺序为m1 m2 m3,而在W2方向上的投影顺序是m2 m3 m1,假设原空间三类样本的相对关系为m1 m2 m3,则W1方向优于W2方向;3) 无法解决大规模分类问题。鉴于此,提出基于流形判别分析的全局保序学习机(global rank preservation learning machine based on manifold-baseddiscriminant analysis, GRPLM)。该方法通过引入流形判别分析[21]来保持样本的全局和局部特征;在最优化问题的约束条件中增加样本中心相对关系限制保证分类决策时考虑样本的相对关系;通过引入核心向量机(core vector machine, CVM)[14]将所提方法适用范围扩展到大规模数据。
本文后续做如下假设:样本集为$T = \{ ({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_N},{y_N})\} \in {(X \times Y)^N}$,其中${x_i} \in X = {R^N},{y_i} \in Y = \{ 1,2, \cdots ,c\} $,类别数为c,各类样本数为${N_i}(1,2, \cdots ,c)$,x为所有样本均值,xi为第i类样本均值。
1 流形判别分析文献[21]提出流形判别分析MDA,流形判别分析引入基于流形的类内离散度(manifold-based Within-classscatter, MWCS)${M_W}$和基于流形的类间离散度(manifold-based between-classscatter, MBCS)${M_B}$两个概念,试图利用Fisher准则,通过最大化${M_B}$和${M_W}$之比获得最佳投影方向。其中,${M_B}$和${M_W}$的定义如下:
| ${M_W} = \mu {S_W} + (1 - \mu ){S_S}$ | (1) |
| ${M_B} = \lambda {S_B} + (1 - \lambda ){S_D}$ | (2) |
式中,$\mu$ 和λ为常数并通过网格搜索策略进行选择;sw和sB分别表示类内离散度和类间离散度,其定义同LDA;sS和sD分别表征同类样本和异类样本的局部结构,两者定义如下:
| ${S_W} = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {({x_{ij}} - {{\bar x}_i}){{({x_{ij}} - {{\bar x}_i})}^{\rm{T}}}} } $ | (3) |
| ${S_B} = \sum\limits_{i = 1}^c {{N_i}({{\bar x}_i} - \bar x){{({{\bar x}_i} - \bar x)}^{\rm{T}}}} $ | (4) |
| ${S_S} = X(S' - S){X^{\rm{T}}}$ | (5) |
式中,$S'$为对角阵且$S' = \sum\nolimits_j {{S_{ij}}}$ 为同类权重函数:
| ${S_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\exp ( - {{\left\| {{x_i} - {x_j}} \right\|}^2}) {y_i} = {y_j}}\\ { 0 {y_i} \ne {y_j} } \end{array}} \right.$ | (6) |
| ${S_D} = X(D - D){X^{\rm{T}}}$ | (7) |
式中,$D'$为对角阵且$D' = \sum\limits_j^ {{D_{ij}}}$ ,其中${D_{ij}}$为异类权重函数:
| ${D_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\exp ( - 1/{{\left\| {{x_i} - {x_j}} \right\|}^2}) {y_i} \ne {y_j}}\\ { 0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_i} = {y_j} } \end{array}} \right.$ | (8) |
MDA的最优化问题定义如下:
| $J = \mathop {\max }\limits_W \frac{{{W^{\rm{T}}}{M_B}W}}{{{W^{\rm{T}}}{M_W}W}} = \mathop {\max }\limits_W \frac{{{W^{\rm{T}}}(\lambda {S_B} + (1 - \lambda ){S_D})W}}{{{W^{\rm{T}}}(\mu {S_W} + (1 - \mu ){S_S})W}}$ | (9) |
GRPLM利用SVM和MDA分别在智能分类和特征提取方面的优势,在分类过程中将样本的全局特征和局部特征以及样本之间相对关系考虑在内,在一定程度上提高分类效率。GRPLM找到的分类超平面具有以下优势:1) 通过引入流形判别分析来保持样本的全局特征和局部特征;2) 通过最小化基于流形的类内离散度,保证同类样本尽可能紧密;3) 通过保持各类样本中心的相对关系不变进而实现保持全体样本的先后顺序不变。
上述思想可表示为如下最优化问题:
| $\mathop {{\rm{min}}}\limits_W {W^{\rm{T}}}{M_W}W - \nu \rho $ | (10) |
| ${W^{\rm{T}}}({m_{i + 1}} - {m_i}) \ge \rho {\rm{ }}i = 1,2, \cdots ,c - 1$ | (11) |
式中,W为分类超平面的法向量;ν为常数并通过网格搜索策略选择;ρ为各类样本间隔;${m_i} = \frac{1}{{{N_i}}}\sum\limits_{k = 1}^{{N_i}} {{x_k}} (i = 1,2, \cdots ,c) $为各类样本均值,c为样本类别数;${W^{\rm{T}}}{M_W}W$表示找到的分类超平面将样本的全局特征和局部特征考虑在内;$\nu \rho $的存在保证各类样本的间隔尽可能大,有利于提高分类精度;式(11)表明GRPLM在分类决策时保持各类样本的相对关系不变。
上述最优化问题的对偶形式如下:
| $\mathop {{\rm{max}}}\limits_\alpha - \sum\limits_{i = 1}^{c - 1} {\sum\limits_{j = 1}^{c - 1} {{\alpha _i}{\alpha _j}{{({m_{i + 1}} - {m_i})}^{\rm{T}}}M_W^{ - 1}({m_{j + 1}} - {m_j})} } $ | (12) |
| $s.t\sum\limits_{i = 1}^{c - 1} {{\alpha _i}} = \nu $ | (13) |
| ${\alpha _i} \ge 0 {\rm{ }} i = 1,2, \cdots ,c - 1$ | (14) |
证明:由Lagrangian定理可得:
| $\begin{array}{l} L(W,\rho ,\alpha ) = {W^{\rm{T}}}{M_W}W - \rho - \\ \sum\limits_{i = 1}^{c - 1} {{\alpha _i}({W^{\rm{T}}}({m_{i + 1}} - {m_i}) - \nu \rho )} \end{array}$ | (15) |
| $\frac{{\partial L}}{{\partial W}} = 0 \Leftrightarrow W = \frac{1}{2}M_W^{ - 1}\sum\limits_{i = 1}^{c - 1} {{\alpha _i}({m_{i + 1}} - {m_i})} $ | (16) |
| $\frac{{\partial L}}{{\partial \rho }} = 0 \Leftrightarrow \sum\limits_{i = 1}^{c - 1} {{\alpha _i}} = \nu $ | (17) |
将式(16)和式(17)带入到式(15),并去掉与研究无关的常数项可得上述对偶式。
2.2 决策函数GRPLM的决策函数为:
| $f(x) = \mathop {\min }\limits_{k \in \{ 1,2, \cdots ,c - 1\} } \{ k:{W^{\rm{T}}}x < {b_k}\} $ | (18) |
假设映射函数Ø满足$\phi :x \to \phi (x)$。原最优化问题的核化形式可表示为:
| $\mathop {{\rm{min}}}\limits_W {W^{\rm{T}}}M_W^\phi W - \nu \rho $ | (19) |
| $s.t{\kern 1pt} {\kern 1pt} {\kern 1pt} {W^{\rm{T}}}(m_{i + 1}^\phi - m_i^\phi ) \ge \rho {\rm{ }}i = 1,2, \cdots ,c - 1$ | (20) |
式中,
| $\begin{array}{c} m_i^\phi = \frac{1}{{{N_i}}}\sum\limits_{k = 1}^{{N_i}} {\phi ({x_k})} (i = 1,2, \cdots ,c)\\ M_W^\phi = \mu S_W^\phi + (1 - \mu )S_S^\phi \\ S_W^\phi = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {{N_i}(\phi ({x_{ij}}) - m_i^\phi ){{(\phi ({x_{ij}}) - m_i^\phi )}^{\rm{T}}}} } \\ S_S^\phi = \sum\limits_{i,j} {(\phi ({x_i})S_{ii}^\phi \phi ({x_i}^{\rm{T}}) - \phi ({x_i})S_{ij}^\phi \phi ({x_i}^{\rm{T}}))} = \\ \phi (X)({{S'}^\phi } - {S^\phi })\phi ({X^{\rm{T}}}) \end{array}$ |
式中,${S'^\phi }$为对角阵且${S'^\phi } = \sum\limits_j^ {S_{ij}^\phi }$ ,其中$S_{ij}^\phi$ 为核同类权重函数:
| $S_{ij}^\phi = \left\{ {\begin{array}{*{20}{c}} {\exp ( - {{\left\| {\phi ({x_i}) - \phi ({x_j})} \right\|}^2}) {y_i} = {y_j}}\\ { 0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_i} \ne {y_j} } \end{array}} \right.$ |
原最优化问题的核化对偶形式为:
| $\begin{array}{l} \mathop {{\rm{max}}}\limits_\alpha - \sum\limits_{i = 1}^{c - 1} {\sum\limits_{j = 1}^{c - 1} {{\alpha _i}{\alpha _j}{{(m_{i + 1}^\phi - m_i^\phi )}^{\rm{T}}}{{(M_W^\phi )}^{ - 1}}(m_{j + 1}^\phi - m_j^\phi )} } \\ s.t\;\;\;\;\;\sum\limits_{i = 1}^{c - 1} {{\alpha _i}} = \nu \\ {\alpha _i} \ge 0 {\rm{ }}i = 1,2, \cdots ,c - 1 \end{array}$ |
GRPLM优化问题求解主要包括大小为NxN矩阵的转置运算以及大小为(c-1)x(c-1)Hessian矩阵QP问题求解运算。大小为NxN矩阵的转置运算的时间复杂度为$O({N^2}\log (N))$,大小为(c-1)x(c-1) Hessian矩阵QP问题求解的时间复杂度为$O({(c - 1)^3})$,GRPLM的时间复杂度为$O({N^2}\log (N)) + O({(c - 1)^3})$,由于c<<N,则GRPLM的时间复杂度近似表示为$O({c^3})$。
2.5 大规模分类 2.5.1 核心向量机核心向量机CVM的基本思路是在大规模样本空间中利用一个逼近率为(1+ε)的近似算法找到核心集,该集合较之原始样本具有比更小的规模。更重要的是,文献[14]指出该核心集与样本数无关,只与参数ε有关,该结论有力地支持了CVM在解决大规模分类问题方面的有效性。
2.5.2 最小包含球最优化问题定义线性形式为:
| ${\rm{min }}{R^2}$ | (21) |
| $s.t.{\left\| {c - {x_i}} \right\|^2} \le {R^2}{\rm{ }}i = 1,2, \cdots ,N$ | (22) |
式中,$c$为超球体球心;$R$为超球体半径。非线性形式为:
| ${\rm{min }}{R^2}$ | (23) |
| $s.t.{\left\| {c - \varphi ({x_i})} \right\|^2} \le {R^2}{\rm{ }}i = 1,2, \cdots ,N$ | (24) |
式中,$\varphi ({x_i})$表示从原始样本空间到高维特征空间的映射。
由Lagrangian定理可得如下对偶形式:
| $\mathop {{\rm{max}}}\limits_\alpha {\rm{ }}{\alpha ^{\rm{T}}}{\rm{diag}}(K) - {\alpha ^{\rm{T}}}{\bf{K}}\alpha $ | (25) |
| $s.t.\;\;\;{\alpha ^{\rm{T}}}1 = 1\alpha \ge 0$ | (26) |
| $\mathop {{\rm{max}}}\limits_\alpha {\rm{ }} - {\alpha ^{\rm{T}}}K\alpha $ | (27) |
令$\beta = \alpha /\nu $,GRPLM的span lang=EN-US>QP形式可转化为:
| $\begin{array}{l} \mathop {{\rm{max}}}\limits_\beta - {\beta ^{\rm{T}}}K\beta \\ s.t\;\;\;\;{\beta ^{\rm{T}}}1 = 1\\ \beta \ge 0 \end{array}$ | (28) |
式中,$K = [{({m_{i + 1}} - {m_i})^{\rm{T}}}M_W^{ - 1}({m_{i + 1}} - {m_i})]$,$1 = {[1,1, \cdots ,1]^{\rm{T}}}$,$0 = {[0,0, \cdots ,0]^{\rm{T}}}$。GRPLM与MEB的对偶形式等价,则可利用CVM解决大规模分类问题。
GRPLM-CVM算法描述如下:
1) 初始化参数;B(c, R):球心为c,半径为R的最小包含球;St:核心集;t:迭代次数;ε:终止参数。
2) 对于$\forall z$有$\varphi (z) \in B({c_t},(1 + \varepsilon )R)$,则转到步骤6),否则转到步骤3);
3) 如果$\varphi (z)$距离球心ct最远,则${S_{t + 1}} = {S_t} \cup \{ \varphi (z)\}$ ;
4) 寻找最新最小包含球B(St+1),并设置:${c_t} = {c_{B({S_{t + 1}})}}$,${R_t} = {R_{B({S_{t + 1}})}}$;
5) t=t+1并转到步骤2);
6) GRPLM对核心集进行训练并得到决策函数。
3 实验分析 3.1 人工数据集人工生成4类服从Gaussian分布的数据集,各类样本50个,其中心点分别为(4,4)、(-3,-3)、(-9,-9)、(-15,-15),均方差均为2.5。人工数据集如图 1a所示。将上述数据集投影到GRPLM找到的方向向量可得图 1b,GRPLM中参数ν选取1。
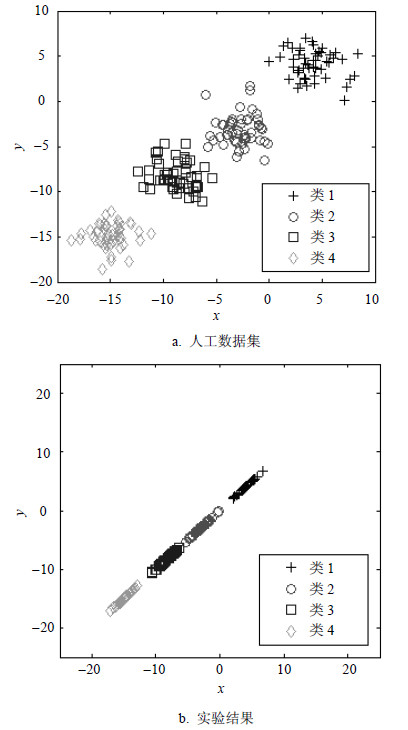 |
| 图1 人工数据集及实验结果 |
由图 1b可以看出,GRPLM找到的方向向量能较好地保持原始数据的相对关系不变,且具有良好的可分性。
3.2 中小规模数据集实验数据集见表 1所示,分别选取实验数据集中各类样本的60%作为训练样本,剩余样本用作测试。
| 表1 中小规模数据集 |
GRPLM的分类性能受核函数选择的影响。本实验将Gaussian核函数、Polynomial核函数、Sigmoid核函数、Epanechnikov核函数,分别带入GRPLM核化形式中来考察GRPLM的分类性能。实验结果如图 2所示。
 |
| 图2 核函数对分类结果的影响 |
由图 2可以看出:在Wine、Liver、Glass、Pima数据集上,选取Gaussian核函数的GRPLM分类精度最优,选取Epanechnikov核函数的GRPLM分类精度次之,选取Sigmoid核函数和Polynomial核函数的GRPLM分类精度分别排在后两位;选取Gaussian核函数和Epanechnikov核函数的GRPLM在Iris数据集上分类精度相同且均具有最优的分类能力。
后续实验选取核函数的依据是:Sigmoid核函数在特定参数下与Gaussian核函数具有近似性能;Polynomial核函数参数较多Polynomial核函数参数较多且较难确定;Gaussian核函数和Epanechnikov核函数在实际中均广泛被使用。但从方便计算角度考虑,后续实验选用Gaussian核函数。
3.2.2 比较实验本节通过与多类支持向量机[22]、K近邻算法比较实验验证GRPLM的有效性。本文实验K取5。Multi-class SVM的最优化表达式如下:
| ${\rm{min }} \frac{1}{2}\sum\limits_{m = 1}^c {{{\left\| {{W_m}} \right\|}^2}} + C\sum\limits_{i = 1}^N {\sum\limits_{m \ne {y_i}} {{\xi _i}^m} } $ | (29) |
| ${\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{W_{{y_i}}}^{\rm{T}}{x_i} + {b_{{y_i}}} \ge {W_m}^{\rm{T}}{x_i} + {b_m} + 2 - {\xi _i}^m$ | (30) |
| $\begin{array}{c} {\xi _i}^m \ge 0{\rm{ }}i = 1,2, \cdots ,c\\ m,{y_i} \in \{ 1,2, \cdots ,c\} ,m \ne {y_i} \end{array}$ | (31) |
| 表2 实验参数表 |
| 表3 中小规模数据集实验结果 |
由表 3可以看出:从平均分类性能看,与Multi-class SVM和KNN相比,GRPLM在UCI数据集上具有更优的分类精度。具体而言,在Wine、Liver、Glass、Pima数据集上GRPLM的分类精度好于Multi-class SVM和KNN;在Iris数据集上GRPLM和Multi-class SVM分类精度相当且略高于KNN。综上所述,GRPLM在中小规模数据集上能较好地完成分类任务。
3.3 大规模数据集 3.3.1 终止参数ε对分类结果的影响实验采用Bank数据集,实验选取60%的数据集用作训练,剩余的用于测试。CVM中的参数ε在网格{10-2, 10-3, 10-4, 10-5, 10-6, 10-7}中选取。GRPLM- CVM的效率受到参数e取值的影响。具体情况参如图 3所示。
 |
| 图3终止参数e对GRPLM-CVM的影响 |
图 3反映的结论是参数ε影响到算法的训练时间以及分类精度。不失一般性,实验选取ε=10-6。
3.3.2 GRPLM-CVM分类性能分析实验采用文献[23]提供的数据集。实验训练样本分别取数据集的20%、40%、60%、80%,从剩下样本中任取500个作为测试样本。实验结果如表 4所示。
| 表4 GRPLM-CVM分类结果 |
由表 4可以看出:随着训练样本规模的增大,GRPLM-CVM分类精度和训练时间呈上升趋势,即训练样本规模影响GRPLM-CVM的分类性能。从分类效果看,GRPLM-CVM基本上能在有限时间内较好地完成分类任务。
4 结 论针对当前分类方法面临的不足,提出基于流形判别分析的全局保序学习机GRPLM。该方法的主要优势在于:1) 进行分类决策时同时考虑样本的全局特征和局部特征;2) 具有保持样本相对关系不变的特性;3) 能在一定程度上解决传统分类器面临的大规模分类问题。与传统分类器的比较实验表明本文所提方法在分类性能方面具有一定优势。但GRPLM仍存在一定问题,如其分类能力对参数的选取较为依赖,如何提高参数选取效率对GRPLM分类性能的提升至关重要,这也是下一步的工作。
| [1] | QUINLAN J R. C4.5: Programs for Machine Learning[M]. San Francisco: Morgan Kaufmann Publishers, 1993. |
| [2] | RASTOGI R, SHIM K. Public: a decision tree classifier that integrates building and pruning[C]//Proc of the Very Large Database Conference (VLDB). New York: [s.n.], 1998: 404-415. |
| [3] | MEHTA M, AGRAWAL R, RISSANEN J. SLIQ: a fast scalable classifier for data mining[C]//Proc of International Conf Extending Database Technology(EDBT'96). France: [s.n.], 1996: 18-32. |
| [4] | GEHRKE J, RAMAKRISHNAN R, GANTI V. Rainforest: a framework for fast decision tree construction of large datasets[J]. Data Mining and Knowledge Discovery, 2000, 4(2-3): 127-162. |
| [5] | LIU B, HSU W, MA Y. Integrating classification and association rule[C]//Proc of the 4th International Conf on Knowledge Discovery and Data Mining. New York, USA: AAAI Press, 1998: 80-86. |
| [6] | LI W M, HAN J, JIAN P. CMAR: Accurate and efficient classification based on multiple class association rules[C] //Proc of IEEE International Conf on Data Mining.Washington D C: IEEE Computer Society, 2001: 369-376. |
| [7] | YIN X, HAN J. Classification based on predictive association rules[C]//SIAM International Conf on Data Mining. San Francisco: [s.n.], 2003: 331-335. |
| [8] | VAPNIK V. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995. |
| [9] | 邓乃扬, 田英杰. 支持向量机——理论、算法与拓展[M]. 北京: 科学出版社, 2009. DENG Nai-yang, TIAN Ying-jie. Support vector machine: Theory, algorithm and development[M]. Beijing: Science Press, 2009. |
| [10] | PAL M, FOODY G M. Feature selection for classification of hyper spectral data by SVM[J]. IEEE Trans on Geoscience and Remote Sensing, 2010, 48(5): 2297-2307. |
| [11] | SCHOLKOPF B, SMOLA A, BARTLET P. New support vector algorithms[J]. Neural Computation, 2000, 12: 1207-1245. |
| [12] | SCHOLKOPF B, PLATT J, SHAWE-TAYLOR J, et a1. Estimating the support of high-dimensional distribution[J]. Neural Computation, 2001, 13: 1443-1471. |
| [13] | TAX D M J, DUIN R P W. Support vector data description [J]. Machine Learning, 2004(54): 45-66. |
| [14] | TSANG I W, KWOK J T, CHEUNG P M. Core vector machines: Fast SVM training on very large data sets[J]. Journal of Machine Learning Research, 2005(6): 363-392. |
| [15] | MANGASARIAN O, MUSICANT D. Lagrange support vector machines[J]. Journal of Machine Learning Research, 200l(1): 161-177. |
| [16] | SUYKENS J A, VANDEWALLE J. Least squares support vector machines classifiers[J]. Neural Processing Letters, 1999, 19(3): 293-300. |
| [17] | LEE Y J, MANGASARIAN O. SSVM: a smooth support vector machines[J]. Computational Optimization and Applications, 2001, 20(1): 5-22. |
| [18] | LANGLEY P, SAGE S. Introduction of selective Bayesian classifier[C]//Proc of the 10th Conf on Uncertainty in Artificial Intelligence. Seattle: Morgan Kaufmann Publishers, 1994: 339-406. |
| [19] | ZHENG Z H, WEBB G I. Lazy Bayesian rules[J]. Machine Learning, 2000, 32(1): 53-84. |
| [20] | FRIEDMAN N, GEIGER D, GOLDSZMIDT M. Bayesian network classifiers[J]. Machine Learing, 1997, 29(2): 131-163. |
| [21] | 刘忠宝, 潘广贞, 赵文娟. 流形判别分析[J]. 电子与信息学报, 2013, 35(9): 2047-2053. LIU Zhong-bao, PAN Guang-zhen, ZHAO Wen-juan. Manifold-based discriminant analysis[J]. Journal of Electroincs & Information Technology, 2013, 35(9): 2047-2053. |
| [22] | WESTON J, WATKINS C. Multi-class support vector machines[R]. London: Department of Computer Science, Royal Holloway University of London Technology, 1998. |
| [23] | LIN L, LIN H T. Ordinal regression by extended binary classification[J]. Advanced in Neural Information Processing Systems, 2007, 19: 865-872. |
 2015, Vol. 44
2015, Vol. 44
