长期以来高可靠、长寿命产品的量化评估是可靠性工程的难题之一[1]。加速试验技术的发展为其提供了一个良好的途径。传统的加速试验均为增应力试验,即恒加应力、步进应力和序进应力,试验终止常采用截尾试验[2]。加速模型和加速试验方法是加速试验技术的两个主要内容。文献[3]基于寿命与应力的概率相关性,建立了一种与现有的加速模型具有同等效力的BEC加速寿命模型。文献[4, 5, 6]在现有的试验方法基础上,提出了一种步降应力加速寿命试验方法(简称步降试验),该试验方法在损耗型长寿命产品的可靠性评估试验中,可明显提高试验效率。文献[7, 8]等基于累计损伤模型对气动缸进行了双应力交叉步降加速寿命试验,得出该试验方法比传统试验方法具有更高的试验精度和试验效率。文献[9]在对数正态分布下对步降和步进试验的效率进行了对比分析,得出步降试验的效率优于步进试验。文献[10, 11]在不同的寿命分布下,进行了双应力交叉步降和步进试验方法的仿真模拟,得出在确定的参数下步降试验比步进更能提高试验效率。文献[12]对双应力交叉步降加速寿命试验进行优化设计,并用Monte Carlo仿真验证了该方法的高效性。文献[13]利用极大似然法,对系统级多应加速寿命数据的模型参数进行了估计,并提出了一种多应力加速试验数据的分析方法。
上述文献对双应力交叉步降、步进试验的效率及数据统计分析进行了研究。结果表明,在确定条件下交叉步降比交叉步进更能缩短试验时间,提高试验效率。但双应力交叉步降、步进试验每次只步降或步进单个应力方向的幅值。用这种方法对重、大型产品进行加速试验,如风力机叶片双轴疲劳加速试验时,仍然存在试验效率较低的问题。
因此,本文提出一种双应力同步步降加速寿命试验方法,将应力的下降改进为同步步降,使其形成一种斜坡式下降轨迹,以提高试验效率。并与双应力交叉步降加速寿命试验方法进行比较分析,验证双应力同步步降加速寿命试验方法的有效性。
1 双应力同步步降加速寿命试验双应力同步步降定数截尾试验是在截尾样本数达到事先规定的截尾数时,将两个加速应力同步降低一级。然后,将样本在低应力下继续进行定数截尾试验。以此类推,直到两应力降至最低加速应力,试验终止。具体的试验步骤描述如下:
1) 设有两组加速应力${{S}^{(1)}}$和${{S}^{(2)}}$,每组应力包含一系列应力水平。正常应力水平分别为$S_{0}^{(1)}$和$S_{0}^{(2)}$,加速应力水平分别为:
| $\left\{ \begin{align} & S_{0}^{(1)}<S_{1}^{(1)}<\cdots <S_{p}^{(1)} \\ & S_{0}^{(2)}<S_{1}^{(2)}<\cdots <S_{q}^{(2)} \\ \end{align} \right.$ | (1) |
2) 从试验产品中随机抽取n个样本,首先置于最高水平组合(p,q)下进行定数截尾试验,记截尾样本数为${{r}_{pq}}$。试验时若有${{r}_{pq}}$个样本发生失效,则将两加速应力在各自的应力级上同步降低一级,使水平组合为$(p-1,q-1)$。
3) 将未失效的$n-{{r}_{pq}}$个样本继续在该水平组合下进行定数截尾试验,记截尾数为${{r}_{(p-1,q-1)}}$。如果有${{r}_{(p-1,q-1)}}$个样本失效,将应力继续同步降低一级,使水平组合为($p-2,q-2$),然后对$n-{{r}_{pq}}-{{r}_{(p-1,q-1)}}$个样本在该应力下作用,进行截尾数为${{r}_{(p-2,q-2)}}$的截尾试验。
4) 以此类推,直到水平组合降至(1,1)级,失效样本数为r11个时,同步步降试验终止,试验轨迹如图 1所示。
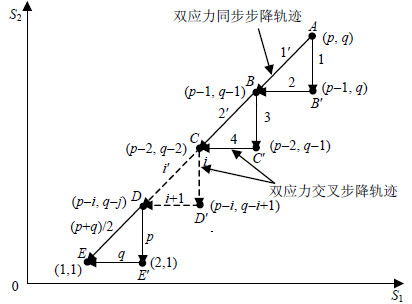 |
| 图1 双应力步降试验轨迹图 |
图 1中,粗斜线ABCDE为本文提出的同步步降试验轨迹,细折线AB'BC'CD'DE'E为交叉步降试验轨迹。由上述轨迹可知,同步步降试验中应力以斜坡式轨迹下降,交叉步降试验中应力以台阶式轨迹下降,两者轨迹有交叉点。为提高试验效率,两加速应力保持$|p-q|\le 1$。
记同步步降试验过程的总步数为:
| $H=\left\{ \begin{align} & \frac{p+q}{2}p=q \\ & \frac{p+q+1}{2}p\ne q \\ \end{align} \right.$ | (2) |
| ${H}'=p+q-1$ | (3) |
将$H$步的各水平组合记为D:
| $D=\left\{ (p,q) \right.,(p-1,q-1),\cdots (2,2),\left. (1,1) \right\}$ | (4) |
| $r={{r}_{pq}}+{{r}_{(p-1,q-1)}}+\cdots +{{r}_{22}}+{{r}_{11}}$ | (5) |
| $\begin{matrix} {{t}_{ij,1}}\le {{t}_{ij,2}}\cdots \le {{t}_{ij,{{r}_{ij}}}} \\ (i,j)\in D\ \text{ }l=1,2,\cdots ,{{r}_{ij}} \\ \end{matrix}$ | (6) |
蒙特卡罗方法是一种通过随机变量的统计试验、随机模拟来求解数学物理、工程技术问题近似解的数值方法。Weibull分布是寿命分布中常用分布之一,用来描述金属材料断裂、绝缘材料老化、传感器及电子元器件等的寿命。本文在Weibull分布下进行双应力同步步降试验的Monte Carlo仿真。
寿命服从Weibull分布时,做如下假定:
1) 产品在正常水平组合$(0,0)$和加速水平组合$(i,j)$下的寿命${{T}_{ij}}$均服从Weibull分布,则寿命分布函数为:
| ${{F}_{ij}}\text{(}t\text{)}=1-\exp \left\{ -{{\left( \frac{t}{{{\eta }_{ij}}} \right)}^{{{m}_{ij}}}} \right\}$ | (7) |
| $t>0,i=0,1,\cdots ,p,j=0,1,\cdots ,q$ |
2) 加速应力下,产品的失效机理保持不变。即在Weibull分布下表征失效机理的形状参数${{m}_{ij}}$保持不变。则有:
| ${{m}_{00}}={{m}_{ij}}\equiv m$ | (8) |
3) 样本的特征寿命${{\eta }_{ij}}$与两个加速应力满足某一加速模型:
| ${{\eta }_{ij}}=\phi ({{S}^{1}},{{S}^{2}})$ | (9) |
双应力加速模型的一般式为[14]:
| $\begin{align} & {{\xi }_{ij}}={{\beta }_{0}}+{{\beta }_{1}}{{\phi }_{1}}(S_{^{i}}^{^{(1)}})+{{\beta }_{2}}{{\phi }_{2}}(S_{j}^{(2)})+{{\beta }_{3}}{{\phi }_{3}}(S_{i}^{(1)},S_{j}^{(2)}) \\ & i=0,1,\cdots ,p,j=0,1,\cdots ,q \\ \end{align}$ | (10) |
加速寿命试验的试验数据中,除第一级应力下的试验数据以外,其余均为多级应力共同作用的结果。因此,对累积试验数据进行折算,从而分离出完整的寿命数据是同步步降试验数据分析的关键。失效数据的转换基于物理原理,利用Nelson累积失效模型进行[15]。
Nelson累积失效模型:产品的残余寿命仅依赖于已累积的失效概率和当前的应力水平,与累积方式无关。其含义为:在应力$({{S}^{(i)}},{{S}^{(j)}})$下,样本工作时间${{\tau }_{ij}}$内累积失效的概率${{F}_{ij}}({{\tau }_{ij}})$相当于该样本在应力(${{S}^{(u)}},{{S}^{(v)}}$)下,工作时间${{\tau }_{uv}}$内的累积失效概率${{F}_{uv}}({{\tau }_{uv}})$,即${{F}_{ij}}({{\tau }_{ij}})={{F}_{uv}}({{\tau }_{uv}})$。代入式(7)可得:
| ${{\tau }_{uv}}/{{\tau }_{ij}}={{\eta }_{uv}}/{{\eta }_{ij}}$ | (11) |
| ${{\tau }_{uv}}=({{\eta }_{uv}}/{{\eta }_{ij}}){{\tau }_{ij}}$ | (12) |
Weibull分布下,同步步降试验的仿真模拟步骤如下:
1) 产生服从Weibull分布的随机样本
若随机变量$X$的分布函数$F(x)$连续,则$r=F(x)$是(0,1)区间上均匀分布的随机变量。由式(7)可知,若令$w=F(x)$,则$w=1-\exp [-{{(t/\eta )}^{m}}]$,w为(0, 1)区间上均匀分布的随机变量。又由于w与1-w在(0, 1)上同分布,则通过逆变换法得Weibull分布的抽样公式为[16]:
| $t=\eta {{(-\ln w)}^{1/m}}$ | (13) |
2) 最高水平组合下的抽样公式
同步步降试验在最高水平组合(p,q)下开始,所以$\eta ={{\eta }_{pq}}$,m已知。因此,最高水平组合下的抽样公式为:
| ${{t}_{{{w}_{k}}}}={{\eta }_{pq}}{{(-\ln {{w}_{k}})}^{1/m}}k=1,2,\cdots ,n$ | (14) |
3) 各水平组合下失效数据的转换
① 将式(14)产生的样本数据从小到大排列,取前$r(r={{r}_{pq}}+{{r}_{(p-1,q-1)}}+\cdots +{{r}_{11}})$个数据作为失效样本,剩余n-r个作为定数截尾的截尾样本。再取前${{r}_{pq}}$个数据的${{t}_{m}}(m=1,2,\cdots ,r_{pq}^{{}})$作为最高水平组合的失效数据。
② 取${{r}_{(p-1,q-1)}}$个数据的tm。此时,$m=({{r}_{pq}}+1,{{r}_{pq}}+2,\cdots ,{{r}_{pq}}+{{r}_{(p-1,q-1)}})$分别减去累积失效时间${{t}_{r,pq}}$,再乘以加速因子${{a}_{pq,(p-1,q-1)}}={{\eta }_{(p-1,q-1)}}/{{\eta }_{pq}}$,即可得水平组合$(p-1,q-1)$下的失效数据。
③ 同理,令$m=({{r}_{pq}}+{{r}_{(p-1,q-1)}}+1,$${{r}_{pq}}+{{r}_{(p-1,q-1)}}+2,\cdots ,{{r}_{pq}}+{{r}_{(p-1,q-1)}}+{{r}_{(p-2,q-2)}})$减去${{t}_{r,(p-1)(q-1)}}$,乘以${{a}_{pq,(p-2,q-2)}}={{\eta }_{(p-2,q-2)}}/{{\eta }_{pq}}$,即得水平组合($p-2,q-2$)下的失效数据。
④ 以此类推,直到得出最低水平组合(1, 1)下的失效数据为止。至此,得到同步步降试验中所有步降应力级下的全部失效数据。
3 实例分析本文的实例源于文献[10],某直流电机寿命服从Weibull分布,形状参数$m=1.5$,对该直流电机进行通断电循环步降加速寿命试验。温度${T}'$(单位为绝对温度)和电压${V}'$(单位为伏特)作为直流电机的两个加速应力,其正常温度水平为${{{T}'}_{0}}=353$,正常电压水平为${{{V}'}_{0}}=100$,设T'和V'的各加速应力分别为:T'1=373,T'2=388,T'3=403,V'1=200,V'2=300,V'3=400,V'4=500。
当样本量N=100,双应力加速模型为:
| $\ln {{\eta }_{pq}}=-20+\frac{20\ 000}{{{T}'}}-4.5\ln {V}'$ | (15) |
用本文提出的双应力同步步降加速寿命试验方法对该实例进行计算机仿真模拟。根据试验步骤得两应力同步步降轨迹为:$(3,4)\to (2,3)\to (1,2)\to (1,1)$。试验总步数$H=(3+4+1)/2=4$。每步定数截尾样本均值为:${{r}_{34}}=23,{{r}_{23}}=17,{{r}_{12}}=6,{{r}_{11}}=5$。利用Matlab进行Monte Carlo仿真模拟,重复仿真300次,得到同步步降试验的失效数据如表 1所示。步降试验是步进试验的逆过程,应力施加具有可复制性。因此,将本文的同步步降方法及原理应用于步进试验,进行双应力同步步进加速寿命试验的仿真模拟。同样重复仿真300次,得到同步步进试验的失效数据如表 2所示。
| 表1 同步步降试验仿真失效数据表(Weibull分布) |
| 表2 同步步进试验仿真失效数据表(Weibull分布) |
表 1、表 2中,数据分别为双应力同步步降、步进加速寿命试验中各加速应力水平组合下,样本从零失效数到规定失效数依次发生失效的累积试验时间,将所有累积试验时间相加,即为整个试验所需的总时间。因此,双应力同步步降、步进加速寿命试验的总时间如表 3所示。并与文献[10]的双应力交叉步降、步进加速寿命试验的总试验时间进行比较。表中时间百分比为本文试验方法的试验时间与文献[10]中对应试验方法的时间之比。
| 表3 试验数据对比表 |
由表 3可知,双应力同步步降试验总时间为交叉步降试验总时间的78.62%,双应力同步步进试验总时间为交叉步进试验总时间的79.61%。因此,双应力同步步降、步进试验相对双应力交叉步降、步进试验,更能缩短试验时间,提高试验效率。
4 结束语1) 为了提高加速寿命试验的效率,本文提出一种双应力同步步降加速寿命试验方法。
2) 在Weibull分布下,双应力同步步降试验比双应力交叉步降试验均更能缩短试验时间,提高试验效率。通过模拟数据的比较分析,验证了双应力同步步降加速寿命试验方法的有效性。
| [1] | 谭伟, 师义民, 孙玉东. 步降应力加速寿命试验的可靠性仿真[J]. 计算机仿真, 2011, 28(12): 80-83. TAN Wei, SHI Yi-min, SUN Yu-dong. Reliability simulation for step-down-stress accelerated life testing[J]. Computer Simulation, 2011, 28(12): 80-83. |
| [2] | MEEKER W Q, ESCOBAR L A. A review of recent research and current issues in accelerated testing[J]. International Statistical Institute(ISI), 1993, 61(1): 147-168. |
| [3] | 安宗文, 黄洪钟, 王贵宝. 基于二维指数条件分布的加速寿命模型[J]. 电子科技大学学报, 2009, 38(3): 455-458. AN Zong-wen, HUANG Hong-zhong, WANG Gui-bao. Accelerated life mode based on bivariate exponential conditional distribution[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(3): 455-458. |
| [4] | 张春华, 陈循, 温熙森. 步降应力加速寿命试验(上篇)-方法篇[J]. 兵工学报, 2005, 26(5): 661-665. ZHANG Chun-hua, CHEN Xun, WEN Xi-sen. Step-down-stress accelerated life test-methodology[J]. Acta Armamentarii, 2005, 26(5): 661-665. |
| [5] | 张春华, 陈循, 温熙森. 步降应力加速寿命验(下篇)-统计分析篇[J]. 兵工学报, 2005, 26(5): 666-669. ZHANG Chun-hua, CHEN Xun, WNE Xi-sen. Step-down-stress accelerated life test-statistical analysis[J]. Acta Armamentarii, 2005, 26(5): 666-669. |
| [6] | 汪亚顺, 张春华, 陈循. 步降应力加速寿命试验(续篇)-优化设计篇[J]. 兵工学报, 2007, 28(6): 686-691. WANG Ya-shun, ZHANG Chun-hua, CHEN Xun. Step-down-stress accelerated life test-optimal design[J]. Acta Armamentarii, 2007, 28(6): 686-691. |
| [7] | CHEN J, WANG D Y, FU Y L, et al. Double-crossed step-stress accelerated life testing for pneumatic cylinder[J]. Applied Mechanics and Materials, 2012, 121-126: 1274-1278. |
| [8] | CHEN J, LI J, WANG D Y, et al. Double crossed step-down-stress accelerated life testing for pneumatic cylinder based on cumulative damage model[J]. Advanced Materials Research, 2014, 871: 56-63. |
| [9] | 徐晓岭, 王蓉华, 於嵩, 等. 对数正态分布步加试验和步降试验的效率比较分析[J]. 机械工程学报, 2009, 45(4): 56-63. XU Xiao-ling, WANG Rong-hua, YU Song, et al. Comparison analysis of efficiencies for lognormal distribution based on step acceleration test and step deceleration test[J]. Journal of Mechanical Engineering, 2009, 45(4): 56-63. |
| [10] | 王玉明, 蔡金燕. 双应力交叉步降加速寿命试验的数值模拟[J]. 计算机仿真, 2008, 25(12): 342-345. WANG Yu-ming, CAI Jin-yan. Numerical simulation of double-cross-step-down-stress accelerated life test[J]. Computer Simulation, 2008, 25(12): 342-345. |
| [11] | 孙玉东, 师义民. 对数正态分布双应力交叉步降试验的仿真分析[J]. 火力与指挥控制, 2012, 37(9): 23-26. SUN Yu-dong, SHI Yi-min. Numerical simulation of double-crossed step-down-stress accelerated life test under lognormal distribution[J]. Fire Control & Command Control, 2012, 37(9): 23-26. |
| [12] | SOUMYA R, CHIRANJIT M. Maximum likelihood analysis of multi-stress accelerated life test data of series systems with competing log-normal causes of failure[J]. Journal of Risk and Reliability, 2015, 229(2): 119-130. |
| [13] | 吕萌, 蔡金燕, 潘刚, 等. 双应力交叉步降加速寿命试验优化设计Monte-Carlo仿真[J]. 电光与控制, 2013, 20(10): 96-101. LÜ Meng, CAI Jin-yan, PAN Gang, et al. Optimal design of double-crossed-step-down-stress accelerated life test based on Monte-Carlo simulation[J]. Electronics Optics & Control, 2013, 20(10): 96-101. |
| [14] | 吴清太, 叶而骅. Weibull分布下两应力交叉定时截尾恒加试验的统计分析[J]. 南昌大学学报(理科版), 1997, 21(3): 251-258. WU Qing-tai, YE Er-hua. Statistical from analysis of type-I censoring data from alternate constant-stress accelerated life testing method under two-parameter Weibull distribution law[J]. Journal of Nanchang University (Natural Science), 1997, 21(3): 251-258. |
| [15] | NELSON W. Accelerated life testing step-stress models and data analysis[J]. IEEE Trans on Reliability, 1980, 29(2): 103-108. |
| [16] | 陈文华, 杨帆, 刘俊俊, 等. 步进应力加速寿命试验方案模拟评价理论与方法[J]. 机械工程学报, 2012, 48(22): 177-181. CHEN Wen-hua, YANG Fan, LIU Jun-jun, et al. Theory and method for simulation evaluation of accelerated life test plan under step-stress[J]. Journal of Mechanical Engineering, 2012, 48(22): 177-181. |
 2016, Vol. 45
2016, Vol. 45
