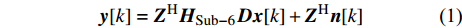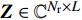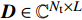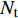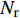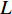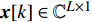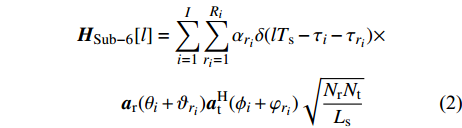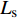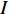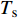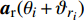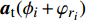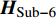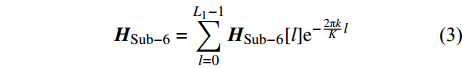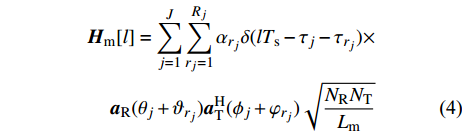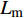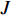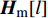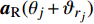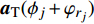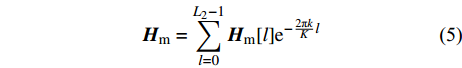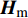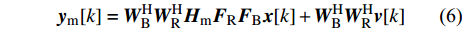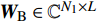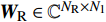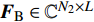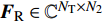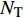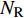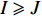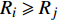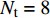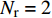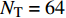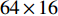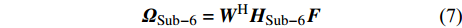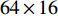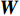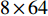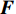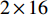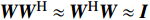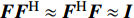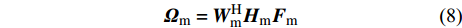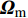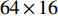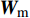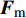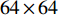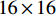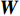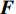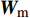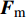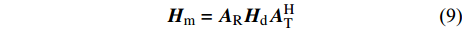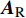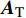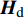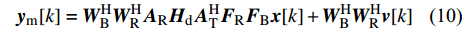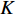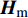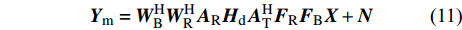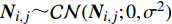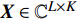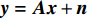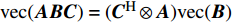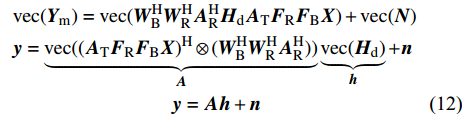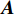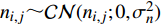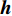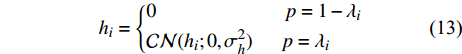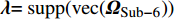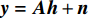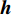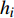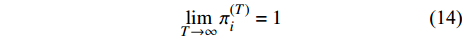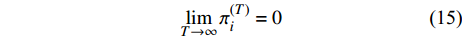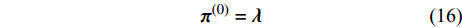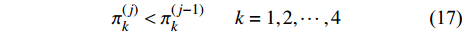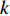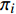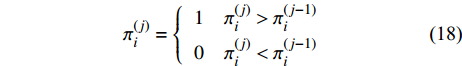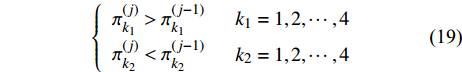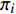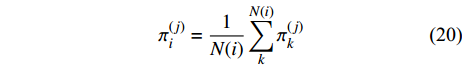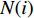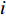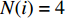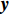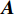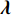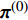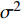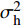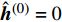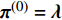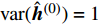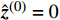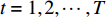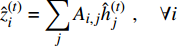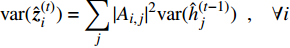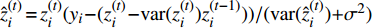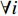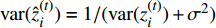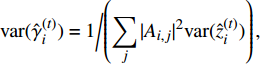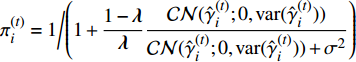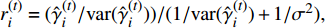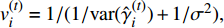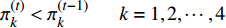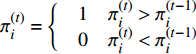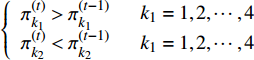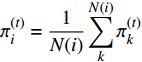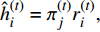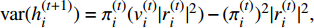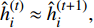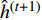Acquisition of Channel State Information Based on K-Learning Sub-6GHz Assist mmWave
-
摘要: 毫米波通信是下一代蜂窝通信之类的大数据通信的可行方案。然而,因为毫米波频率具有极大的路径损耗,所以为了减轻毫米波路径损耗,混合模拟/数字波束成形可以作为一种技术来降低路径损耗。对于获得高波束源增益至关重要的是在发射机处获得准确的毫米波信道信息。该文着重讨论具有大规模MIMO阵列的毫米波通信系统中的信道状态信息获取问题。由于信道信息获取是一种开销很大的方法,因此该文考虑了一种开销低的精确信道估计方案。通过在子-6GHz处提取的支持信息来辅助毫米波信道信息的获取,将毫米波信道信息获取公式化为压缩感测问题,并使用广义近似消息传递(GAMP)算法获得信道信息。使用子-6GHz信道的支持分布信息扩展了GAMP算法。此外,基于K最近邻的思想,根据子-6GHz的支持分布信息重新设计GAMP算法。仿真结果表明,与现有的信道估计算法相比,该算法不仅可以提高估计精度还能降低导频开销。Abstract: Millimeter-wave (mmWave) communication is a practicable scheme for big data communication, such as next-generation cellular communication. However, mmWave frequencies have an extremely large path loss, for this, hybrid analog/digital beamforming could serve as an awesome technique to reduce such loss. This paper concentrates on the channel state information acquirement problem in mmWave communication systems with massive multiple-input multiple-output (MIMO) arrays. Because the channel state information acquirement is a method of significant overhead, we consider an accurate channel estimation scheme with low overhead. This paper proposes using support information extracted at Sub-6GHz to aid the mmWave channel state information acquirement. We formulate mmWave channel state information acquirement as a compressive sensing problem and use generalized approximate message passing (GAMP) algorithm. We also extend the GAMP algorithm with support distribution information from Sub-6GHz channel. Furthermore, based on the K nearest neighbor idea, we redesign the GAMP algorithm depending on Sub-6GHz support distribution information. Simulation results show that the out-of-band information aided mmWave channel estimation is capable of reducing the pilot overhead greatly and channel estimation accuracy can be improved as well.
-
在5G通信中,信道估计是一个重要问题。特别是对于毫米波(mmWave)大规模多输入多输出(MIMO)系统,只有通过获取准确的信道信息才能设计混合预编码矩阵。为了获取mmWave大MIMO系统的信道信息,压缩感知(compressed sensing, CS)技术已经被广泛地应用。利用mmWave信道的稀疏性,CS技术可以极大地提高信道估计精度。在CS算法中,广义近似信息流(GAMP)算法是一个重要技术。尽管GAMP算法具有性能好、低复杂度等特点,但是由于mmWave通信系统中采用模拟预编码器,导致接收信号维度大幅减少,这对信道估计非常不利,即便采用GAMP算法也不能实现高的估计精度。根据文献[1-2],发现如果知道稀疏信号中非零元素的位置即支撑集信息,GAMP算法的性能将会得到极大提高,还能减少训练信号开销,提高符号利用率。在之前的研究中,假设非零元素位置信息是已知的。但是这个假设在实际中是不合理的,为此可以利用文献[3]提供的子-6GHz(Sub-6GHz)和mmWave信道的空间一致性来获取支撑集信息。
尽管Sub-6GHz信道和mmWave信道存在大量不同,二者的信道模型有时是不通用的[4],然而,它们在空间上存在一致性[5-6]。当位置和阵列排布方式相同时,二者在到达角、离开角和角度功率谱上存在一致性,称这种一致性为空间一致[7]。
本文利用Sub-6GHz信道和mmWave信道的空间一致性来获取mmWave支撑集分布,将获取的分布信息作为GAMP算法的先验信息,然后结合K学习更新先验信息,得到K-GAMP算法。仿真结果表明K-GAMP算法可减少导频开销,提高估计精度。
1. 系统模型
本文中,
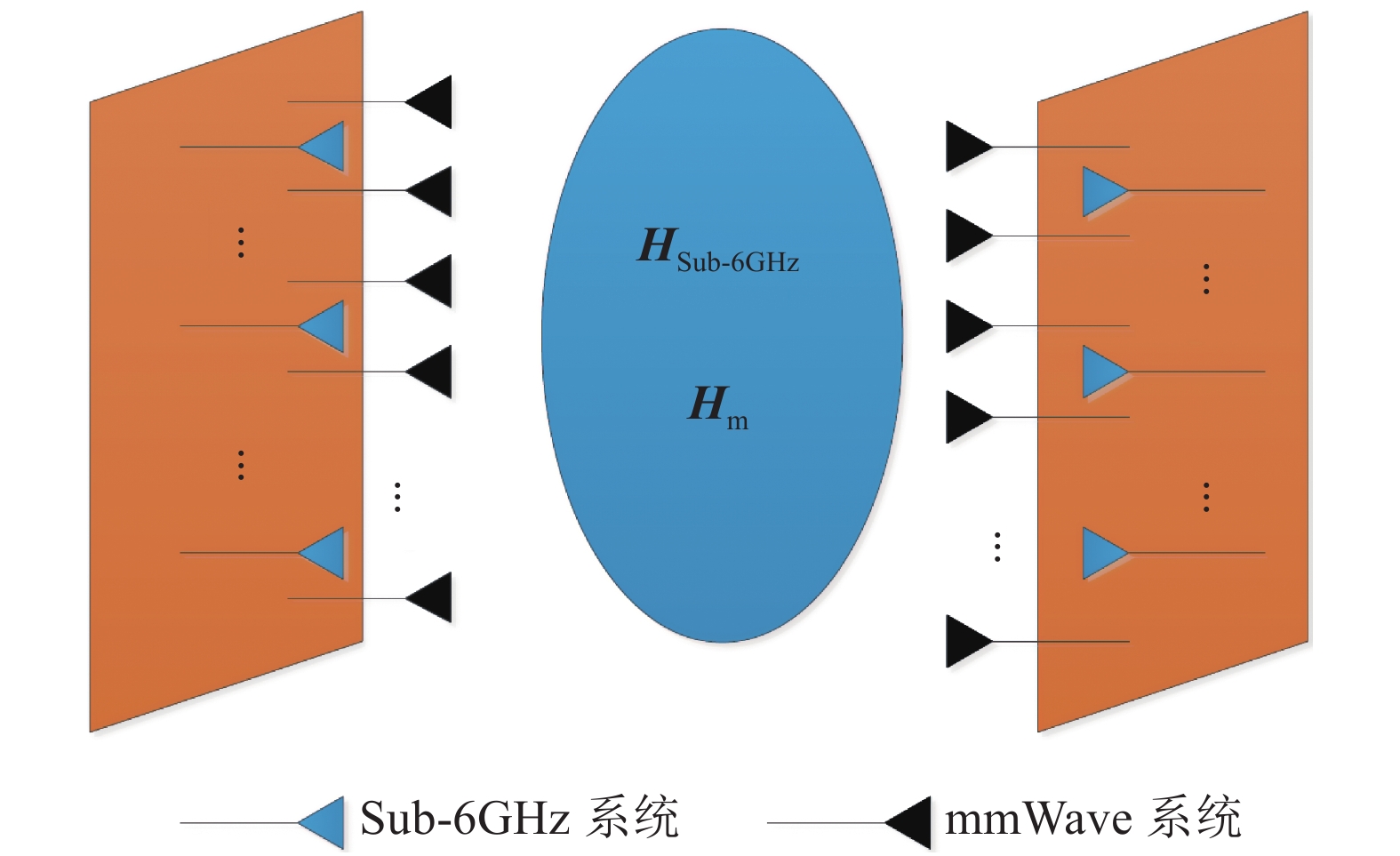
${{A}}$ 和${{a}}$ 分别表示矩阵和向量,${{{a}}_i}$ 表示${{a}}$ 中的第$i$ 个元素,${{{A}}_{i,j}}$ 是${{A}}$ 中第$(i,j)$ 个元素。转置运算、共轭运算和共轭转置运算分别表示为${( \cdot )^{\rm{T}}}$ 、${( \cdot )^{\rm{*}}}$ 和${( \cdot )^{\rm{H}}}$ 。${\mathbb{E}}[ \cdot ]$ 是期望运算并且${\rm{var}} ( \cdot )$ 为方差运算。$\delta ( \cdot )$ 表示冲激响应函数。${\mathbb{C}}$ 和${\mathbb{R}}$ 分别表示实数域和复数域。${\cal{C}}{\cal{N}}(x;a,b)$ 是满足方差为$b$ 、均值为0的高斯分布的变量$x$ 。图1为一个包括Sub-6GHz和mmWave的双基站系统。
图1双基站系统中Sub-6GHz天线阵列和mmWave天线阵列为均匀线性阵列并且二者是共址的(即平行排列)。下面给出Sub-6GHz和mmWave的系统模型。
Sub-6GHz系统是一个全数字系统,所以Sub-6GHz的接收信号为:
$${{y}}[k] = {{{Z}}^{\rm{H}}}{{{H}}_{{\rm{Sub - 6}}}}{{Dx}}[k] + {{{Z}}^{\rm{H}}}{{n}}[k]$$ (1) 式中,
${{Z}} \in {{\mathbb{C}}^{{N_{\rm{r}}} \times L}}$ 为组合矩阵;${{D}} \in {{\mathbb{C}}^{{N_{\rm{t}}} \times L}}$ 为预编码矩阵;${N_{\rm{t}}}$ 和${N_{\rm{r}}}$ 分别为发射天线和接收天线数;$L$ 为数据流长度;${{x}}{\rm{[}}k{\rm{]}} \in {{\mathbb{C}}^{L \times 1}}$ 为发射数据流。因为要利用Sub-6GHz信道和mmWave信道的空间一致性,所以采用几何信道建模方法。时延域的Sub-6GHz信道为:$$ \begin{split} & {{{H}}_{{\rm{Sub - 6}}}}[l] = \sum\limits_{i = 1}^I {\sum\limits_{{r_i} = 1}^{{R_i}} {{\alpha _{{r_i}}}\delta (l{T_{\rm{s}}} - {\tau _i} - {\tau _{{r_i}}}) \times } } \\ & \qquad\;{{{a}}_{\rm{r}}}({\theta _i} + {\vartheta _{{r_i}}}){{a}}_{\rm{t}}^{\rm{H}}({\phi _i} + {\varphi _{{r_i}}})\sqrt {\frac{{{N_{\rm{r}}}{N_{\rm{t}}}}}{{{L_{\rm{s}}}}}} \end{split}$$ (2) 式中,
${L_{\rm{s}}}$ 为路径衰落因子;$I$ 是信道路径数量;${T_{\rm{s}}}$ 为OFDM符号间隔;${{{a}}_{\rm{r}}}({\theta _i} + {\vartheta _{{r_i}}})$ 和${{{a}}_{\rm{t}}}({\phi _i} + {\varphi _{{r_i}}})$ 分别为接收阵列响应和发射阵列响应向量。频域信道${{{H}}_{{\rm{Sub - 6}}}}$ 能通过傅里叶变换得到:$${{{H}}_{{\rm{Sub - 6}}}} = \sum\limits_{l = 0}^{{L_1} - 1} {{{{H}}_{{\rm{Sub - 6}}}}[l]{{\rm{e}}^{ - \frac{{2{\text π}k}}{K}l}}} $$ (3) 同样,对于mmWave信道,可以表示为:
$$ \begin{split} {{{H}}_{\rm{m}}}[l] = \sum\limits_{j = 1}^J {\sum\limits_{{r_j} = 1}^{{R_j}} {{\alpha _{{r_j}}}\delta (l{T_{\rm s}} - {\tau _j} - {\tau _{{r_j}}})} } \times \\ {{{a}}_{\rm{R}}}({\theta _j} + {\vartheta _{{r_j}}}){{a}}_{\rm{T}}^{\rm{H}}({\phi _j} + {\varphi _{{r_j}}})\sqrt {\frac{{{N_{\rm{R}}}{N_{\rm{T}}}}}{{{L_{\rm{m}}}}}} \end{split}$$ (4) 式中,
${L_{\rm{m}}}$ 为路径衰落因子;$J$ 是信道路径数量;${{{H}}_{\rm{m}}}[l]$ 表示mmWave时延域信道;${{{a}}_{\rm{R}}}({\theta _j} + {\vartheta _{{r_j}}})$ 和${{{a}}_{\rm{T}}}({\phi _j} + {\varphi _{{r_j}}})$ 分别表示发射端和接收端的阵列响应向量。同样,用傅里叶变换能得到mmWave频域信道为:$${{{H}}_{\rm{m}}} = \sum\limits_{l = 0}^{{L_2} - 1} {{{{H}}_{\rm{m}}}[l]{{\rm{e}}^{ - \frac{{2{{\text π}}k}}{K}l}}} $$ (5) 式中,
${{{H}}_{\rm{m}}}$ 是mmWave频域信道。mmWave接收信号为:$${{{y}}_{\rm{m}}}[k] = {{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{{H}}_{\rm{m}}}{{{F}}_{\rm{R}}}{{{F}}_{\rm B}}{{x}}{\rm{[}}k{\rm{]}} + {{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{v}}{\rm{[}}k{\rm{]}}$$ (6) 式中,
${{{W}}_{\rm{B}}} \in {{\mathbb{C}}^{{N_1} \times L}}$ 和${{{W}}_{\rm{R}}} \in {{\mathbb{C}}^{{N_{\rm{R}}} \times {N_1}}}$ 分别表示接收端的模拟组合矩阵和数字组合矩阵;${{{F}}_{\rm{B}}} \in {{\mathbb{C}}^{{N_2} \times L}}$ 和${{{F}}_{\rm{R}}} \in {{\mathbb{C}}^{{N_{\rm{T}}} \times {N_2}}}$ 表示发射端的数字预编码和模拟预编码矩阵;${N_{\rm{T}}}$ 和${N_{\rm{R}}}$ 表示发射天线和接收天线。通过研究之前的工作不难发现以下规律:1) 信道特性随频率而变化,并且差异随着载波频率的增加而增加;2) 具有延迟特性的多径对频率具有依赖性;3) 某些路径可能会以一个频率呈现。4) Sub-6GHz和mmWave的路径数满足规律$I \geqslant J$ 和${R_i} \geqslant {R_j}$ 。这些性质在仿真中将被用到。下面讨论Sub-6GHz和mmWave信道的空间一致性。由于空间一致性常常表现为Sub-6GHz和mmWave信道的支撑集位置存在重合,所以将空间一致性也称为支撑集一致性。2. 基于Sub-6GHz信道提取毫米波信道支撑集信息
由于Sub-6GHz信道和mmWave信道的维度不相同,设计预编码矩阵将Sub-6GHz信道的维度进行扩展,然后获取mmWave支撑集信息。Sub-6GHz系统的发射天线数
${N_{\rm{t}}} = 8$ ,接收天线数${N_{\rm{r}}} = 2$ ,因此Sub-6GHz信道就是一个$8 \times 2$ 的矩阵。mmWave系统的发射天线数${N_{\rm{T}}} = 64$ ,接收天线数${N_{\rm{R}}} = 16$ ,mmWave信道是一个$64 \times 16$ 的矩阵。根据文献[5-6]给出的矩阵提取Sub-6GHz信道支撑集信息为:$${{{\varOmega}} _{{\rm{Sub - 6}}}} = {{{W}}^{\rm{H}}}{{{H}}_{{\rm{Sub - 6}}}}{{F}}$$ (7) 式中,
${{{\varOmega}} _{{\rm{Sub - 6}}}}$ 是$64 \times 16$ 的矩阵;${{W}}$ 是$8 \times 64$ 的矩阵;${{F}}$ 是$2 \times 16$ 的矩阵。根据文献[8],${{W}}{{{W}}^{\rm{H}}} \approx {{{W}}^{\rm{H}}}{{W}} \approx {{I}}$ ,${{F}}{{{F}}^{\rm{H}}} \approx {{{F}}^{\rm{H}}}{{F}} \approx {{I}}$ ,其中,I是单位矩阵。同样,通过调整mmWave系统的模拟预编码矩阵和数字预编码矩阵也能得到mmWave的支撑集分布信息为:$${{{\varOmega}} _{\rm{m}}} = {{W}}_{\rm{m}}^{\rm{H}}{{{H}}_{\rm{m}}}{{{F}}_{\rm{m}}}$$ (8) 式中,
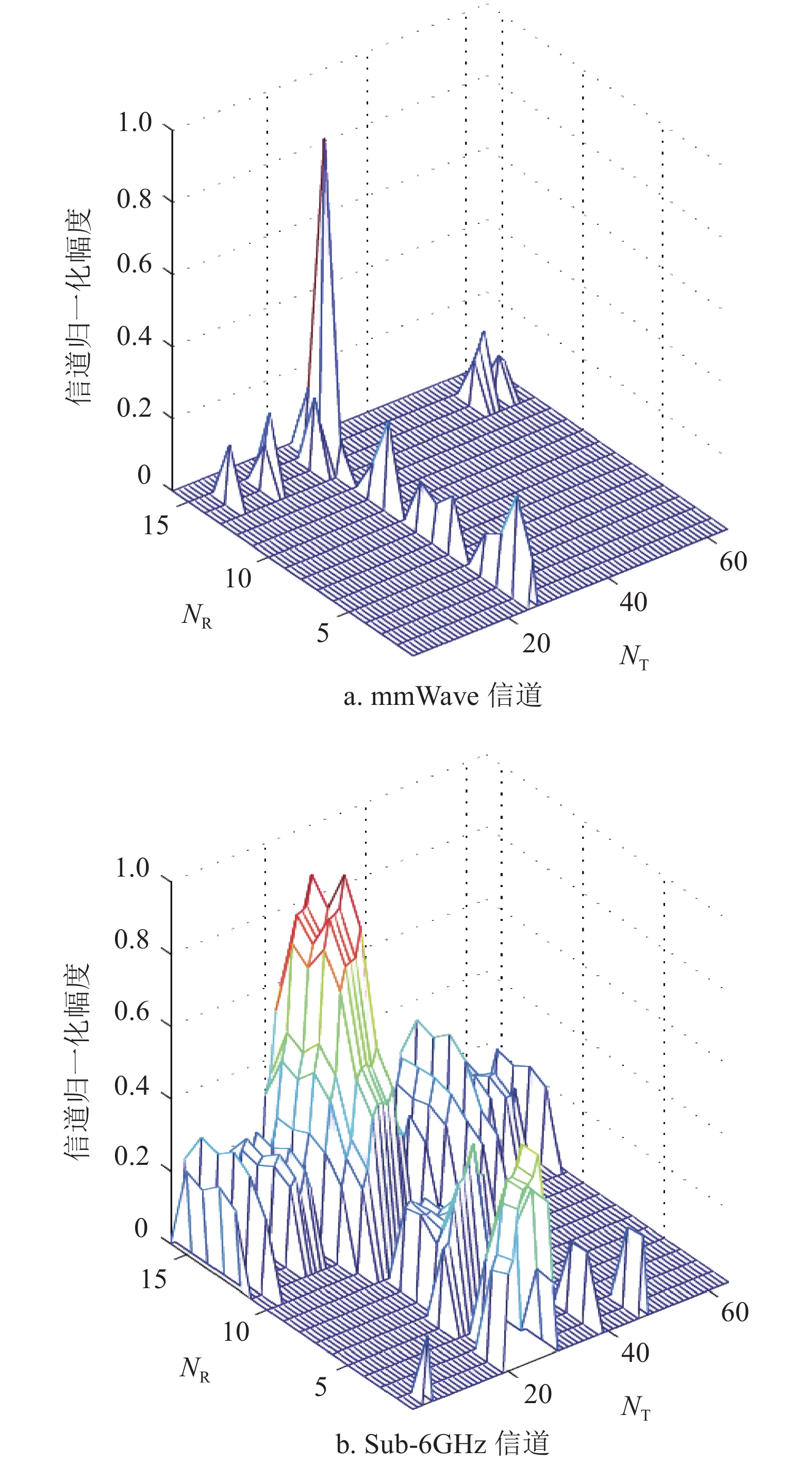
${{{\varOmega}} _{\rm{m}}}$ 是$64 \times 16$ 的矩阵;${{{W}}_{\rm{m}}}$ 和${{{F}}_{\rm{m}}}$ 分别为$64 \times 64$ 和$16 \times 16$ 的矩阵。仿真结果如图2所示。由图2可以看出:首先,由于矩阵
${{W}}$ 和${{F}}$ 、${{{W}}_{\rm{m}}}$ 和${{{F}}_{\rm{m}}}$ 满足近似酉矩阵特性,所以二者经过这种变换后不会改变信道的功率;其次,mmWave的支撑集位置信息和Sub-6GHz的支撑集位置信息是重合的,即${\rm{supp(}}{{{\varOmega}} _{\rm{m}}}{\rm{)}} \subset {\rm{supp(}}{{{\varOmega}} _{{\rm{Sub - 6}}}}{\rm{)}}$ 。Sub-6GHz提供了mmWave信道的支撑集分布信息,但是这个支撑集信息是粗略的,可以视为先验信息。下面介绍问题公式和如何利用K学习来更新先验信息。3. 问题公式
为了应用CS技术,将式(5)化简为:
$${{{H}}_{\rm{m}}} = {{{A}}_{\rm{R}}}{{{H}}_{\rm{d}}}{{A}}_{\rm{T}}^{\rm{H}}$$ (9) 式中,
${{{A}}_{\rm{R}}}$ 和${{{A}}_{\rm{T}}}$ 分别为接收端和发射端的阵列响应矩阵;${{{H}}_{\rm{d}}}$ 为时延域稀疏信道矩阵。将式(9)代入式(6)中,有:$${{{y}}_{\rm{m}}}[k] = {{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{{A}}_{\rm{R}}}{{{H}}_{\rm{d}}}{{A}}_{\rm{T}}^{\rm{H}}{{{F}}_{\rm{R}}}{{{F}}_{\rm{B}}}{{x}}{\rm{[}}k{\rm{]}} + {{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{v}}[k]$$ (10) 假设使用了
$K$ 个子载波并且信道${{{H}}_{\rm{m}}}$ 是准静态信道,式(10)进一步整理为:$${{{Y}}_{\rm{m}}} = {{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{{A}}_{\rm{R}}}{{{H}}_{\rm{d}}}{{A}}_{\rm{T}}^{\rm{H}}{{{F}}_{\rm{R}}}{{{F}}_{\rm{B}}}{{X}} + {{N}}$$ (11) 式中,
${{{N}}_{i,j}} \sim {\cal{C}}{\cal{N}}({{{N}}_{i,j}};0,{\sigma ^2})$ 为高斯白噪声;${{X}} \in {{\mathbb{C}}^{L \times K}}$ 为导频矩阵。只有将问题公式化简为${{y}} = {{Ax}} + {{n}}$ 的形式,才能应用CS技术。根据矩阵向量化公式${\rm{vec}} ({{ABC}}) = ({{{C}}^{\rm{H}}} \otimes {{A}}){\rm{vec}} ({{B}})$ ,式(11)化简为:$$ \begin{split} & {\rm{vec}} ({{{Y}}_{\rm{m}}}) = {\rm{vec}} ({{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{A}}_{\rm{R}}^{\rm{H}}{{{H}}_{\rm{d}}}{{{A}}_{\rm{T}}}{{{F}}_{\rm{R}}}{{{F}}_{\rm{B}}}{{X}}) + {\rm{vec}} ({{N}})\\ & {{y}} = \underbrace {{\rm{vec}} ({{({{{A}}_{\rm{T}}}{{{F}}_{\rm{R}}}{{{F}}_{\rm{B}}}{{X}})}^{\rm{H}}} \otimes ({{W}}_{\rm{B}}^{\rm{H}}{{W}}_{\rm{R}}^{\rm{H}}{{A}}_{\rm{R}}^{\rm{H}}))}_{{A}}\underbrace {{\rm{vec}} ({{{H}}_{\rm{d}}})}_{{h}} + {{n}}\\ & \qquad\qquad\qquad\qquad{{y}} = {{Ah}} + {{n}} \end{split} $$ (12) 式中,
${{A}}$ 为感知矩阵;${{{n}}_{i,j}} \sim {\cal{C}}{\cal{N}}({{{n}}_{i,j}};0,\sigma _n^2)$ 同样满足高斯分布。至此,信道估计问题转化为CS处理的典型问题。根据文献[9],${{h}}$ 中的元素满足伯努利高斯分布:$${{{h}}_i} = \left\{ {\begin{aligned} & 0\qquad\qquad\quad\quad\;\;{p = 1 - {{{\lambda}} _i}} \\ & {{\cal{C}}{\cal{N}}({{{h}}_i};0,\sigma _h^2)}\quad\;\;{p = {{{\lambda}} _i}} \end{aligned}} \right.$$ (13) 根据上面叙述,已知了mmWave信道的支撑集信息
${{\lambda}} {\rm{ = supp(}}{\rm{vec}} ({{{\varOmega}} _{{\rm{Sub - 6}}}}){\rm{)}}$ 和问题公式${{y}} = {{Ah}} + {{n}}$ 。下面介绍K-GAMP算法。4. 基于K学习的广义近似信息流算法(K-GAMP)
本文利用K学习的思想,根据文献[10],在原有的GAMP算法中首先要对支撑集的位置进行判断,使用π表示位置向量。当估计向量
${{h}}$ 中的元素${{{h}}_i}$ 为非零元素时,且算法迭代次数$T$ 足够时,有:$$\mathop {\lim }\limits_{T \to \infty } {{\pi}} _i^{(T)} = 1$$ (14) 当估计向量中的元素
${{{h}}_i}$ 为零元素时,有:$$\mathop {\lim }\limits_{T \to \infty } {{\pi}} _i^{(T)} = 0$$ (15) 由于估计向量维度过大,使算法GAMP的导频开销变的极大。利用估计的信道作预编码时,不需要零元素,所以在信道估计中只考虑非零元素,这样会极大缩小估计数量且减少导频开销[11],通过使用Sub-6GHz提供的支撑集信息可以实现这个目标。将示性向量函数
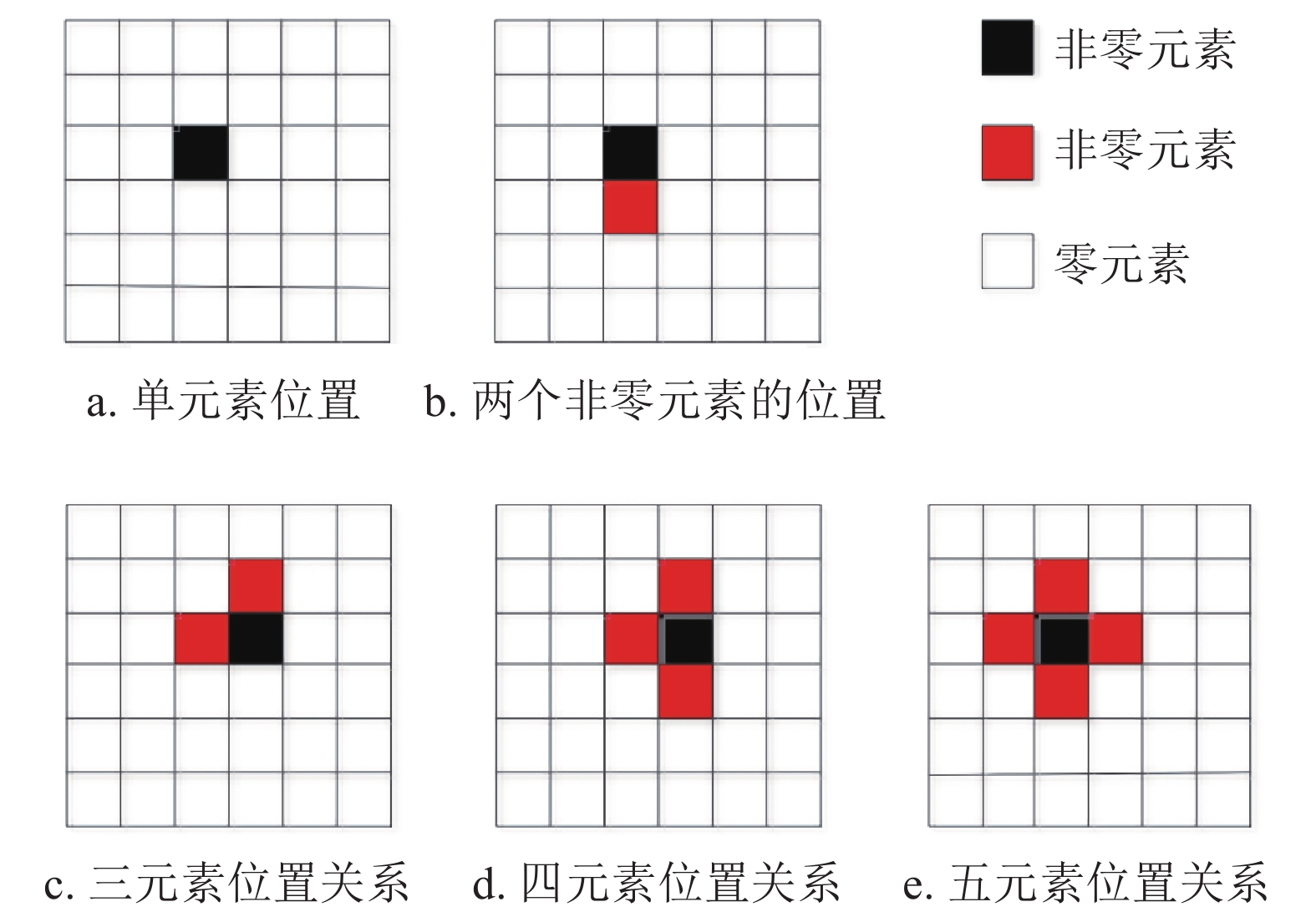
${{\pi}} $ 的初始迭代值设为:$${{{\pi}} ^{(0)}} = {{\lambda}} $$ (16) 由于Sub-6GHz信道提供的是粗略估计信息,所以要缩小这个初始值。利用K学习的方法进行判断,给出如图3所示的非零元素的位置关系。
如图3a所示,如果非零元周围都是零元素,存在如下的关系:
$${{\pi}} _k^{(j)} < {{\pi}} _k^{(j - 1)}\begin{array}{*{20}{c}} {}&{k = 1,2, \cdots ,4} \end{array}$$ (17) 由于非零元周围最多有4个相邻元素,所以
$k$ 在1~4之间变化。如果非零元素周围满足式(17),变量${{{\pi}} _i}$ 在第j次迭代为:$${{{\pi}} }_i^{(j)} = \left\{\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{{{{\pi}} }_i^{(j)} > {{{\pi}} }_i^{(j - 1)}} \end{array}} \\ {\begin{array}{*{20}{c}} 0&{{{{\pi}} }_i^{(j)} < {{{\pi}} }_i^{(j - 1)}} \end{array}} \end{array}} \right.$$ (18) 非零元素的位置关系如图3b~图3e所示,非零元素周围的元素将会表现为如下两种关系:
$$\left\{ {\begin{array}{*{20}{c}} {{{{\pi}} }_{{k_1}}^{(j)} > {{{\pi}} }_{{k_1}}^{(j - 1)}\begin{array}{*{20}{c}} {}&{{k_1} = 1,2, \cdots ,4} \end{array}} \\ {{{{\pi}} }_{{k_2}}^{(j)} < {{{\pi}} }_{{k_2}}^{(j - 1)}\begin{array}{*{20}{c}} {}&{{k_2} = 1,2, \cdots ,4} \end{array}} \end{array}} \right.$$ (19) 根据K学习思想,非零元素位置
${{{\pi}} _i}$ 为:$${{\pi}} _i^{(j)} = \frac{1}{{N(i)}}\sum\limits_k^{N(i)} {{{\pi}} _k^{(j)}} $$ (20) 式中,
$N(i)$ 表示非零元素$i$ 周围元素的个数,由于采用4阶K学习算法,所以本文中$N(i) = 4$ 。K-GAMP的算法如下:
输入:
${{y}}$ ,${{A}}$ ,$\lambda $ ,${{{\pi}} ^{(0)}}$ ,${{{\sigma}} ^2}$ ,${{\sigma}} _{\rm{h}}^{\rm{2}}$ 初始化:
${\hat{{h}}^{(0)}} = 0$ ,${{{\pi}} ^{(0)}} = \lambda $ ,${\rm{var}} ({\hat{{h}}^{(0)}}) = 1$ ,${\hat { z}^{(0)}} = 0$ 1) for
$ t = 1,2, \cdots ,T$ 2)
$ {\hat{ z}}_i^{(t)} = \displaystyle\sum\limits_j {{{{A}}_{i,j}}{{\hat{{h}}}}{{_j^{\left( t \right)}}}} \;\,,\quad \forall i$ 3)
$ {\rm{var}} ({\hat{ z}}_i^{(t)}) = \displaystyle\sum\limits_j {|{{{A}}_{i,j}}{|^2}} {\rm{var}} ({{\hat{{h}}}}_j^{(t - 1)})\begin{array}{*{20}{c}} ,&{\forall i} \end{array}$ 4)
$ {\hat{ z}}_i^{(t)} \!=\! {{z}}_i^{(t)}{({{{y}}_i}\! -\! ({{z}}_i^{(t)} \!-\! {\rm{var}} ({{z}}_i^{(t)}){{z}}_i^{(t - 1)}))} / {({\rm{var}} ({\hat{ z}}_i^{(t)}) +} {\sigma ^2}) $ ,${\forall i}$ 5)
$ {\rm{var}} ({\hat{ z}}_i^{(t)}) = {1 / {({\rm{var}} ({{z}}_i^{(t)}) + {\sigma ^2})}}$ 6)
$ {\rm{var}} ({\hat{ \gamma }}_i^{(t)}) = {1 \bigg/ {\left(\displaystyle\sum\limits_j {|{{{A}}_{i,j}}{|^2}} {\rm{var}} ({\hat{ z}}_i^{(t)})\right),}}$ 7)
$ {{{\pi}} }_i^{(t)} = {1 \bigg/ {\left( {1 + \dfrac{{1 - \lambda }}{\lambda }\dfrac{{{\cal{C}}{\cal{N}}({\hat{ \gamma }}_i^{(t)};0,{\rm{var}} ({\hat{ \gamma }}_i^{(t)}))}}{{{\cal{C}}{\cal{N}}({\hat{ \gamma }}_i^{(t)};0,{\rm{var}} ({\hat{ \gamma }}_i^{(t)})) + {\sigma ^2}}}} \right)}}$ ,8)
$ r_i^{(t)} = {{({{{\hat{ \gamma }}_i^{(t)}} / {{\rm{var}} ({\hat{ \gamma }}_i^{(t)})}})} / {({1 / {{\rm{var}} ({\hat{ \gamma }}_i^{(t)})}} + {1 / {{\sigma ^2}}})}},$ 9)
$ v_i^{(t)} = {1 / {({1 / {{\rm{var}} ({\hat{ \gamma }} _i^{(t)})}} + {1 / {{\sigma ^2}}})}},$ 10) if
$ {{{\pi}} }_k^{(t)} < {{{\pi}} }_k^{(t - 1)}\begin{array}{*{20}{c}} {}&{k = 1,2, \cdots ,4} \end{array}$ 11)
$ {{{\pi}} }_i^{(t)} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{{{{\pi}} }_i^{(t)} > {{{\pi}} }_i^{(t - 1)}} \end{array}} \\ {\begin{array}{*{20}{c}} 0&{{{{\pi}} }_i^{(t)} < {{{\pi}} }_i^{(t - 1)}} \end{array}} \end{array}} \right.$ 12) else if
$ \left\{ {\begin{array}{*{20}{c}} {{{{\pi}} }_{{k_1}}^{(t)} > {{{\pi}} }_{{k_1}}^{(t - 1)}\begin{array}{*{20}{c}} {}&{{k_1} = 1,2, \cdots ,4} \end{array}} \\ {{{{\pi}} }_{{k_2}}^{(t)} < {{{\pi}} }_{{k_2}}^{(t - 1)}\begin{array}{*{20}{c}} {}&{{k_1} = 1,2, \cdots ,4} \end{array}} \end{array}} \right.$ 13)
$ {{{\pi}} }_i^{(t)} = \dfrac{1}{{N(i)}}\displaystyle\sum\limits_k^{N(i)} {{{{\pi}} }_k^{(t)}}$ 14) end
15) end
16)
$ {{\hat{{h}}}}_i^{(t)} = {{{\pi}} }_j^{(t)}{{r}}_i^{(t)},$ 17)
$ {\rm{var}} ({{h}}_i^{(t + 1)}) = {{{\pi}} }_i^{(t)}({{v}}_i^{(t)}|{{r}}_i^{(t)}{|^2}) - {({{{\pi}} }_i^{(t)})^2}|{{r}}_i^{(t)}{|^2},$ 18) while
$ {{\hat{{h}}}}_i^{(t)} \approx {{\hat{{h}}}}_i^{(t + 1)},$ 19) end
20) end
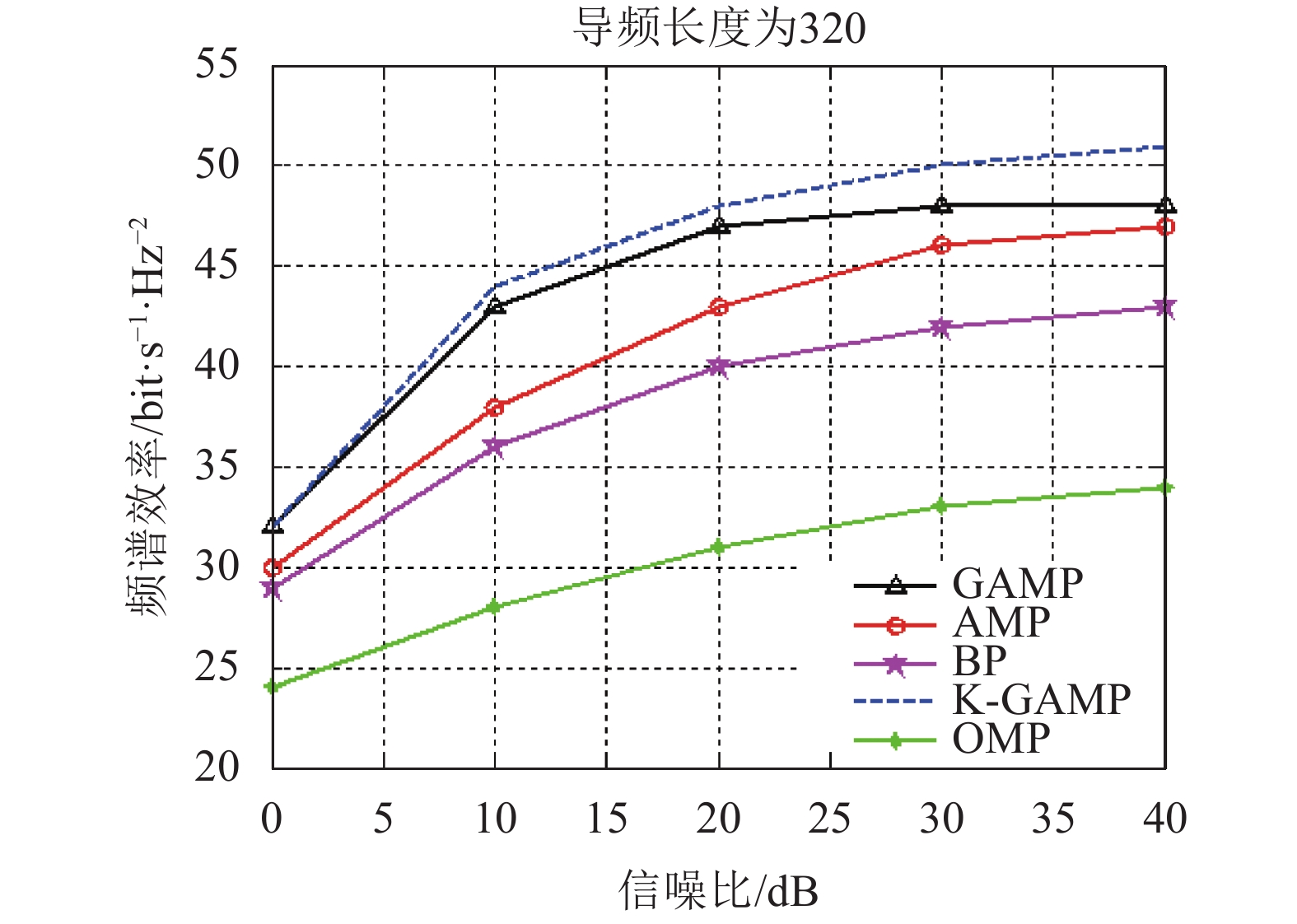
21) 输出:
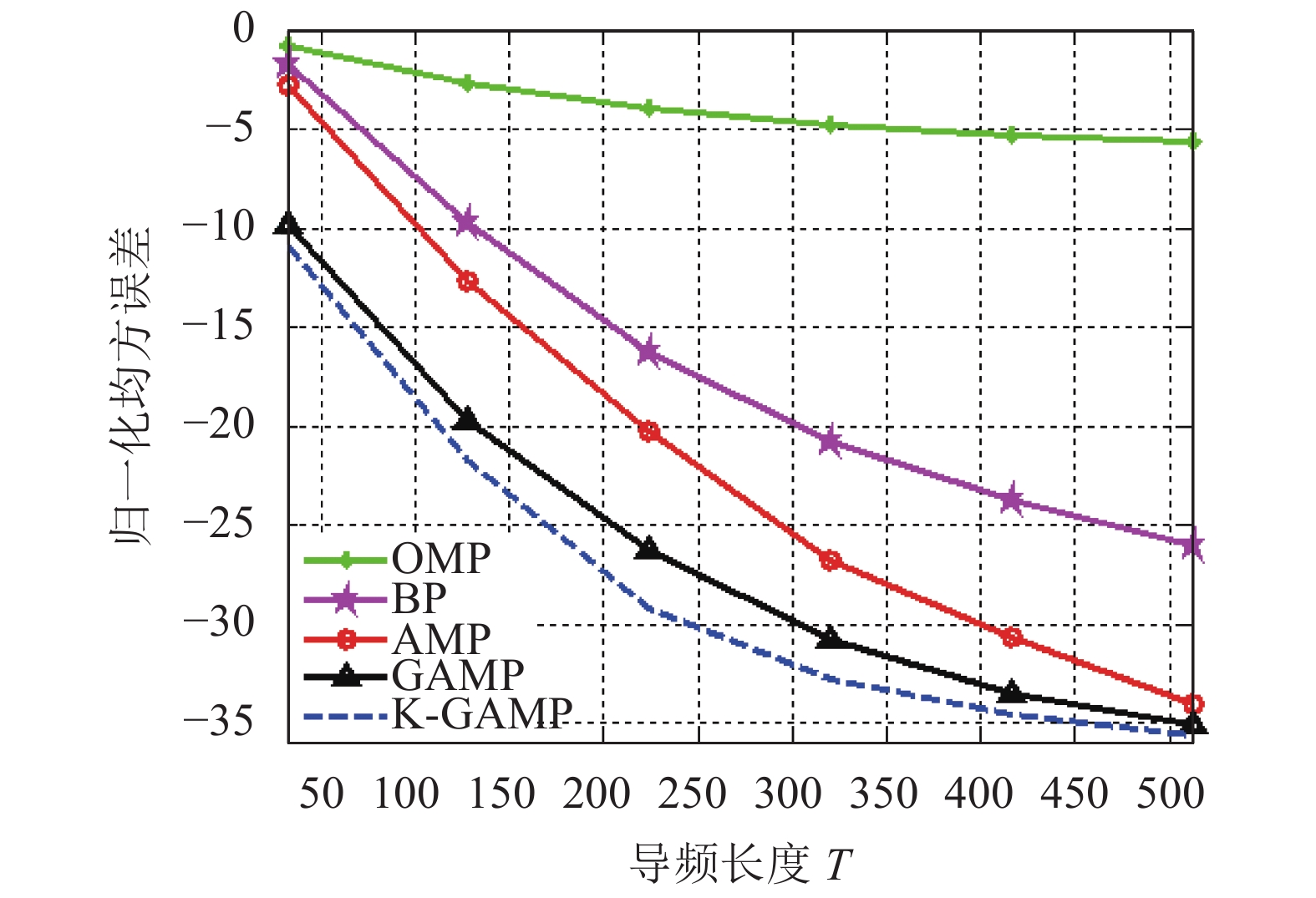
$ \hat {{h}}_{}^{(t + 1)}$ 本文在文献[12]中GAMP算法的基础上给出了结合了Sub-6GHz信道提供的支撑集信息的GAMP算法,即K-GAMP算法。由于文章篇幅有限,不再重复文献[12]中的GAMP算法。下面通过仿真结果来说明改进的K-GAMP算法的性能。
5. 仿真结果
在分析中,考虑一个发射天线数为64、接收天线数为16的大MIMO mmWave系统。Sub-6GHz系统的发射接收天线数分别为8和2。除此之外,mmWave信道服从独立复高斯分布,在Sub-6GHz中获取的是完美的信道信息。
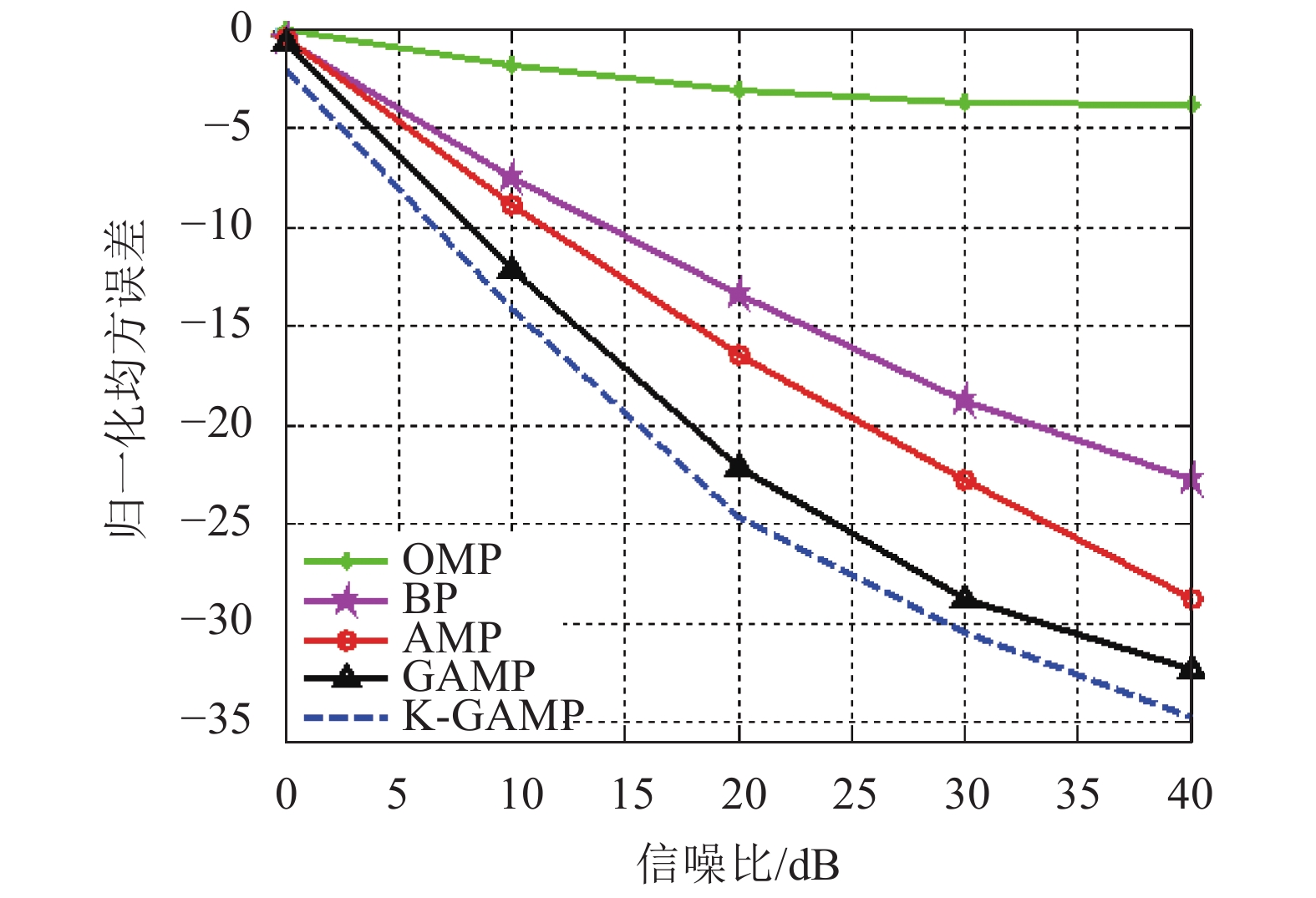
K-GAMP算法与导频开销和信噪比的比较分析分别如图4和图5所示,在仿真中使用归一化均方误差对估计精度进行评估。通过比较发现相比于传统的GAMP算法,本文提出的K-GAMP不仅在估计精度上取得了很大提高,也极大地减少了导频开销。从图4和图5中发现传统的OMP算法在这种系统中几乎不能正常工作。在图6中,通过比较5种算法给系统带来的频谱效率提升来衡量算法的性能。同样,本文的K-GAMP在提升频谱效率上仍然是最好的。
6. 结 束 语
本文针对混合毫米波系统信道估计问题,通过利用Sub-6GHz信道和mmWave信道的空间一致性确定mmWave非零元素位置信息。在此基础上给出了一种全新的信道估计算法K-GAMP。仿真结果表明,利用Sub-6GHz辅助mmWave信道估计可以大幅减少导频开销和提高估计精度。此外,与现有的算法相比,还能显著提高系统频谱效率。
-
[1] WANG Wen-yuan, XIU Yue, LI Bin-rui, et al. FDD downlink channel estimation solution with common sparsity learning algorithm and zero-partition enhanced GAMP algorithm[J]. IEEE Access, 2018, 16(6): 11123-11145.
[2] WANG Wen-yuan, XIU Yue, ZHANG Zhong-pei. FDD massive MIMO downlink channel estimation with complex hybrid generalized approximate message passing algorithm[J]. J Ambient Intell Humanized Comput, 2017, DOI: 10.1007/s12652-017-0634-x.
[3] GONZELEZ-PELCIC N, ALI A, VA V, et al. Millimeter-wave communication with out-of-band information[J]. IEEE Commun Mag, 2017, 55(12): 140-146. DOI: 10.1109/MCOM.2017.1700207
[4] HASHEMI M, KOKSAL C E, SHROFF N B. Out-of-band millimeter wave beamforming and communications to achieve low latency and high energy efficiency in 5G systems[J]. IEEE Trans Commun, 2018, 66(2): 875-888. DOI: 10.1109/TCOMM.2017.2771308
[5] JIANG Z, MOLISCH A F, CAIRE G. Achievable rates of FDD massive MIMO systems with spatial channel correlation[J]. IEEE Transactions on Wireless Communications, 2015, 14(5): 2868-2882. DOI: 10.1109/TWC.2015.2396058
[6] PETER M, AKI K, KATSUYUKI H. Measurement campaigns and initial channel models for preferred suitable frequency ranges[EB/OL]. [2016-03-20]. https://bscw.5g-mmmagic.eu/pub/bscw.cgi/d94832.
[7] ROH W, SEOL J Y, PARK J, et al. Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results[J]. IEEE Commun Mag, 2014, 52(2): 106-113. DOI: 10.1109/MCOM.2014.6736750
[8] SEMIARI O, SAAD W, BENNIS M, et al. Integrated millimeter wave and Sub-6GHz wireless networks: a roadmap for ultra-reliable low-latency communications[EB/OL]. [2018-02-12]. https://arxiv.org/abs/1802.03837.
[9] WIPF D P, RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Trans Signal Process, 2007, 55(7): 3704-3716. DOI: 10.1109/TSP.2007.894265
[10] LIN Xin-cong, WU Sheng, JIANG Chun-xiao, et al. Estimation of broadband multiuser millimeter wave massive MIMO-OFDM channels by exploiting their sparse structure[J]. IEEE Trans Wireless Commun, 2018, 17(6): 3959-3973. DOI: 10.1109/TWC.2018.2818142
[11] XIU Y, WANG W, WU J, et al. Massive MIMO downlink channel estimation based on improved CAMP-MMV algorithm[C]//2017 9th International Conference on Advanced Infocomm Technology (ICAIT). [S.l.]: IEEE, 2017: 114-119.
[12] RANGAN S. Generalized approximate message passing for estimation with random linear mixing[C]//2011 IEEE International Symposium on Information Theory Proceedings. St Petersbug, Russia: IEEE, 2011: 2168-2172.
-
期刊类型引用(4)
1. 南作用,钟志刚,陈任翔,王亚. 考虑传输损耗的无线通信毫米波信道建模分析. 计算机仿真. 2025(02): 531-535 .  百度学术
百度学术
2. 陈璐,任志雄,刘赛,时连存,刘寰宇. 毫米波辅助治疗类风湿关节炎的有效性及对机体免疫、炎性反应的影响. 吉林医学. 2023(02): 330-332 .  百度学术
百度学术
3. 孙长印,毛亚宁,江帆,王军选. 基于无监督DNN和Sub-6GHz的毫米波功率控制算法. 西安邮电大学学报. 2023(02): 29-38 .  百度学术
百度学术
4. 孙长印,刘李延,江帆,姜静. 基于DNN的Sub-6 GHz辅助毫米波网络功率分配算法. 通信学报. 2021(09): 184-193 .  百度学术
百度学术
其他类型引用(3)

 ISSN
ISSN 


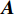
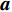
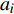
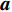
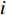
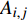
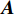

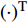
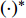
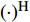
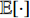
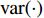
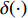


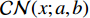
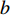
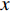
 下载:
下载: