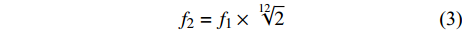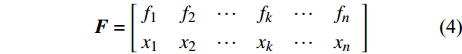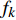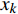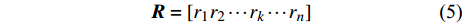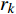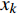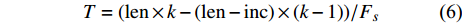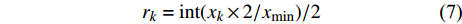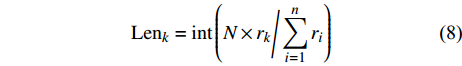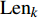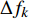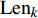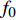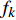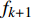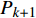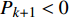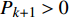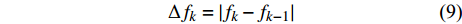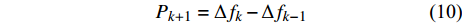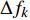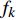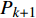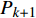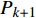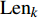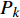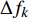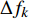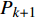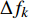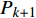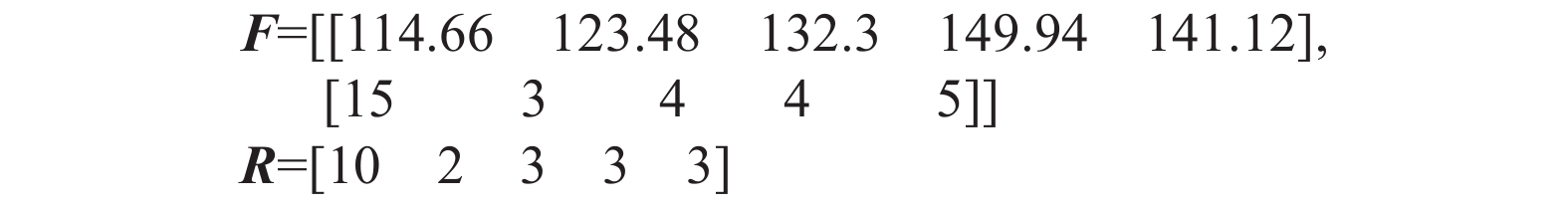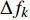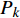An Improved Iterative Algorithm for Humming Tune Recognition and Notation
-
摘要: 哼唱记谱是音乐创作谱曲的重要方法与过程。该文分析了受多种环境因素影响的复杂哼唱音频基本特征;基于加窗傅里叶变换方法,以音符为单位对哼唱音频进行区域性的划分、定义和特征提取,提出了以相对振幅为依据快速提取基频的方法,设计出一种可变区域的傅里叶变换迭代算法。采用Python 3.6编程实现了上述迭代算法,自动获取哼唱音符的音高和音长并形成数字乐谱,实验测试准确率达到84.3%。上述结果表明,该算法能更加精确地识别哼唱曲调,为开发精准辅助作曲软件提供了一种可行的识别与记谱算法,具有较好的应用前景。Abstract: Humming notation is an important method and process of composing music. Considering the complexity of humming audio and the influence of various environmental factors, this paper analyzes the basic characteristics of humming audio. On the basis of windowed Fourier Transform, the humming audio is regionally divided, defined and extracted according to the notes. A method of fast extraction of fundamental frequency is proposed based on relative amplitude of humming audio. And further a variable-region Fourier Transform iteration algorithm is designed and implemented programmatically by Python 3.6. This iteration algorithm can recognize humming melody more accurately, obtain the pitch and length of each note of humming, and automatically form a digital music score. The accuracy of the experimental test reached 84.3%. The achieved results show that the algorithm can identify humming tunes more accurately, thus it would be a feasible recognition and notation algorithm for developing composing-assisting software with good application prospects.
-
音乐是构建人类文明、传承文化、表达思想情感的艺术和重要途径,人类社会发展离不开音乐。随着网络的发展,数字音乐用户逐渐普及。仅2015年,中国数字音乐市场规模就达近500亿[1],音乐创作步入了数字时代。在音乐创作中,通过哼唱形成曲谱是音乐创作过程中必不可少的重要过程与方法[2]。哼唱曲调人工写作曲谱难度大,一般只有专业音乐人才能完成,且目前没有成熟的通用辅助软件。如果可以通过手机APP软件完成哼唱直接转换为乐谱,无疑将会帮助更多人进入音乐创作行业。因此,设计一种快速精准识别哼唱曲调的算法与软件,实现自动记谱具有广阔的应用前景和市场。
对哼唱的曲调的识别,通常的方法是采用寻找音频频率的突变点,并对音符音长进行切分,然后提取切分段的频率。频率的提取主要有时域、频域以及统计3种方法[3]。当前应用较多的是频域分析方法,主要有离散小波变换(DWT)和加窗傅里叶变换(WFT)2种。离散小波变换主要的特征是灵活性、快速性、双域性和深刻性[4],但是对音高频率相差只有几赫兹的人声低频部分,提取误差较大。而加窗傅里叶变换通过简单调整窗长,可以较好地满足需求。
在使用加窗傅里叶变换提取基频的方法中,国内外已经做了较多的报导。文献[5]提出了自适应的短时傅里叶变换(ASTFT),利用自适应关系调整窗长;但自适应调整需要提前知道目标参数,与哼唱基频提取的目标相悖。文献[6]提出了多分辨率快速傅里叶变换(FFT)的正弦提取;虽然提高了和弦音频的提取能力,但准确度只有71.4%,并且与哼唱记谱的基频提取要求仍有差距。文献[7]采用了加窗傅里叶变化提取人声哼唱音高,通过对谐波分组来确定基频;但其固定窗长的提取方法无法同时满足高频和低频提取的精确度。文献[8]采用多分辨率短时离散傅里叶变换(STDFT)对音频的主旋律进行提取,并指出应在局部区域对频率不断变化的音频进行频率测量;但该工作追求对谐波的提取,适合对一般音乐信号的处理,含有大量的乐器噪声,与哼唱记谱中的基频提取背景不符。人声哼唱的能量很难固定,波动较大,因此,对哼唱的音符度量(频率、音高、音长)的精确识别,成为解决辅助作曲软件的技术关键点,也是难点。不同人的发音标准、声音大小、节奏情况相对不同,再加上哼唱环境影响导致音频组成更加复杂,节奏变化模糊,随机性更大,因此在对人声哼唱的音频的精确提取方面,更具挑战性。
综上所述,对于人声哼唱的自动识别记谱方面,当前并没有成熟且完美的解决方案。本文在基于加窗傅里叶变换基础上,提出了一种新的符合哼唱特征的加窗傅里叶变换改进算法,较好地解决了对哼唱作曲过程中音频的分析与提取,为开发精准的哼唱作曲软件,提供了一种关键技术和解决方案。
1. 哼唱基频提取
哼唱的基频频率一般为80~1 600 Hz,基频是哼唱中的重要特征,基频的频率决定了哼唱的音高。当前通常采用谐波分析法提取哼唱基频[7-10],即通过找出部分谐波,再通过谐波频率推测基频频率,但是谐波频率并不一定恰好出现在基频的整数倍上,尤其体现在含谐波频率较多的哼唱低频部分[7],还容易将基频误判为实际值的一半或一倍。因此使用谐波分析的误差较大。本文对多种大量实际的哼唱音频进行采样分析,发现基频的峰值通常出现在振幅第一次达到最大振幅的1/10左右处。为了进一步得到更精确的基频,采用式(1)对得出的基频进行修正。这种利用最大振幅直接提取基频的方法明显克服了谐波分析方法的不足。
$$ f' = [{f_{1/10}}] + 2 \times F_{\!s}/N $$ (1) 式中,
$f'$ 是修正后的频率;$[{f_{1/10}}]$ 是第一次出现的不超过最大振幅1/10对应的频率值;$F_s$ 是离散数字哼唱音频对原始连续声音信号的采样率;$N$ 是离散数字哼唱音频信号的采样点数。利用最大振幅直接提取基频的方法必须尽可能地降低噪声能量,突出基频峰峰值,并防止频谱泄漏。加窗傅里叶变化为此提供了一种解决方案,常用的窗函数有固定矩形(Rectangular)窗、汉宁(Hanning)窗、布莱克曼(Blackman)窗和海明(Hamming)窗[7,11]。由于海明窗对音频频谱泄漏与噪声处理的效果最好[12],因此本文采用了海明窗函数减少噪声对音频数字信号基频提取的影响,表达式为:
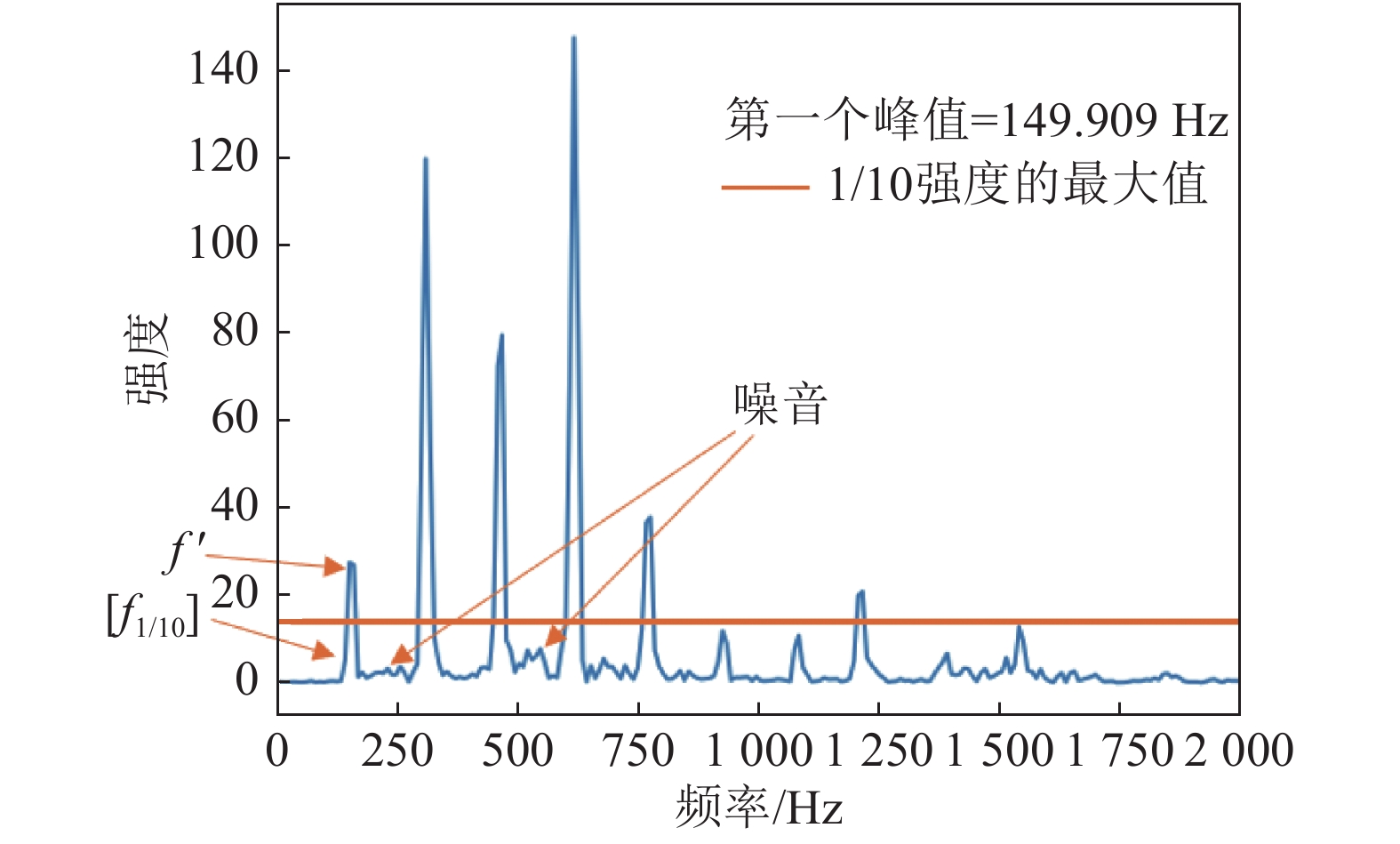
$$ w(n) = 0.54 - 0.46\cos \frac{{2n{\text π} }}{\rm {len}}{\rm{ }}\quad 1 \leqslant n \leqslant {\rm {len}} $$ (2) 图1显示了一段0.1 s、147 HZ的哼唱音频的幅频关系,以及其对应的
$f'$ 和$[{f_{1/10}}]$ 。由基频可以推算出音高,一般采用国际标准音高(standard pitch)度量,按照高度顺序分别为A、Bb、B、C、C#、D、Eb、E、F、F#、G、G#,越靠后表示半音高度越高。2个半音高度之间的频率关系为[7]:
$$ {f_2} = {f_1} \times \sqrt[{12}]{2} $$ (3) 式中,f1和f2分别是2个音高对应的频率,且f1比f2低一个半音高度。这样就可以计算出所有频率和音高的对应关系。
2. 哼唱记谱识别流程与算法
2.1 哼唱音频识别流程
整个哼唱的识别记谱,就是对音频信号进行合理切分、精确提取哼唱特征信息的过程。基本流程如图2所示。初始化参数后,通过分帧来获取基频-时间关系;通过构建可识别频率矩阵、节拍规律矩阵来实现对音符音长识别区域的切分;通过提出并实现基于加窗傅里叶变化迭代算法来对基频进行精确识别和对音符音长识别区域切分的修正;最后应用国际标准音高度量换算式(3)输出数字乐谱。
2.2 有效哼唱音符音长区域切分
按上述流程,对离散数字哼唱音频信号进行分帧,再逐帧进行哼唱基频提取,就可以得到频率-时间信息[13]。由于在哼唱基频的范围内(80~1 600 Hz),2个最低音频率E2(82.406 Hz)与F2(87.308 Hz)仅相差4.902 Hz,对于采样率为44.1 kHz的离散数字哼唱音频,帧长至少应为8 997个采样点以保证足够的分辨率。但由于人哼唱的音符音长最短为0.1 s,若取8 997个采样点作为帧长,则会严重丢失音符音长为0.1 s的唱音信息,故本文取5 000个采样点作为帧长,以提高获取频率-时间信息的分辨率。
获取频率-时间信息后,需要快速寻找音频的突变,从而实现对音符音长区域切分[14]。在切分算法实现过程中,构建了频率矩阵F和节拍矩阵R。频率矩阵F用于记录唱音的出现频率和其连续出现的次数。
$$ { F} = \left[\!\!\! {\begin{array}{*{20}{c}} {{f_1}}&{{f_2}}& \cdots &{{f_k}}& \cdots &{{f_n}} \\ {{x_1}}&{{x_2}}& \cdots &{{x_k}}& \cdots &{{x_n}} \end{array}} \right] $$ (4) 式中,
${f_k}$ 是第k个连续出现最多次的唱音频率,简称第k个频率;${x_k}$ 是该唱音频率复现的帧数。矩阵R用于记录音长区域的切分值,即形成哼唱识别的节奏,表达如下:$${ R} = [{r_1}{\rm{ }}{r_2}{\rm{ }} \cdots {\rm{ }}{r_k}{\rm{ }} \cdots {\rm{ }}{r_n}]$$ (5) 式中,
${r_k}$ 是第k个频率的唱音拍数。${x_{\min }}$ 是F矩阵中${x_k}$ 的最小值,k、n均为整数。节奏是多个单音持续时间的关系,即音符音长关系,它是哼唱音符切分的重要依据,可认为是哼唱单音的持续时间。其值可由分帧时产生的帧长和帧移2个参数计算,通常两帧之间会有重叠部分。对一定帧数的时长计算有:
$$T = ({\rm {len}} \times k - ({\rm {len}} - {\rm {inc}}) \times (k - 1))/F_s$$ (6) 式中,T为时长;len为帧长;k为帧数;inc为帧移;Fs为采样率。为了准确提取哼唱节奏,本文取最短音符音长为一拍,并将所有节奏修正为一拍的整数或半整倍。修正公式为:
$${r_k} = \operatorname{int} ({x_k} \times 2/{x_{\min }})/2$$ (7) 对音频信号的切分为:
$${{\rm {Len}}_k} = \operatorname{int} \left( {N \times {r_k}\Bigg/\sum\limits_{i = 1}^n {{r_i}} } \right)$$ (8) 式中,
${{\rm {Len}}_k}$ 是第k个区域所含的音频信号采样点数;N为离散数字哼唱音频信号采样点的总数。有效哼唱音符音长区域切分算法如图3所示。2.3 哼唱可变区域傅里叶精确识别迭代算法
虽然海明窗函数能够较好地处理音频频谱泄漏和噪声,由于人声哼唱音频普遍复杂,且受日常环境等多种因素影响,单一采样这种方法识别,往往出现漏、错、变调现象,难以达到更加精准地识别音符音长和音高。为此,本文在上述识别区域基础上,进一步改进算法,并统一进行了修正。
改进算法的基本原理是:假定一个唱音在已经切分区域内频率近似不变,通过不断迭代更改区域的大小,计算一个频率变化率
$\Delta {f_k}$ 的最小点来确定哼唱基频,并以该点出现时的区域所含采样点个数来计算该音的音符音长。首先判断哼唱频率变化方向,确定边界改变的初始方向。选择或者定义一个可变识别区域${{\rm {Len}}_k}$ ,k值为[a,b]。向右扩大区域(增大b值),令初始区域对应的基频为${f_0}$ ,向右扩展2次区域的基频对应值为${f_k}$ 、${f_{k + 1}}$ 。对这3个数据求出变化阻尼${P_{k + 1}}$ ,若${P_{k + 1}} < 0$ ,则应该沿增大b的方向继续迭代;若${P_{k + 1}} > 0$ ,则初始化b值后应该沿减小b的方向迭代。定义基频变化率和变化阻尼分别为:
$$ \Delta {f_k} = |{f_k} - {f_{k - 1}}| $$ (9) $$ {P_{k + 1}} = \Delta {f_k} - \Delta {f_{k - 1}} $$ (10) 式中,
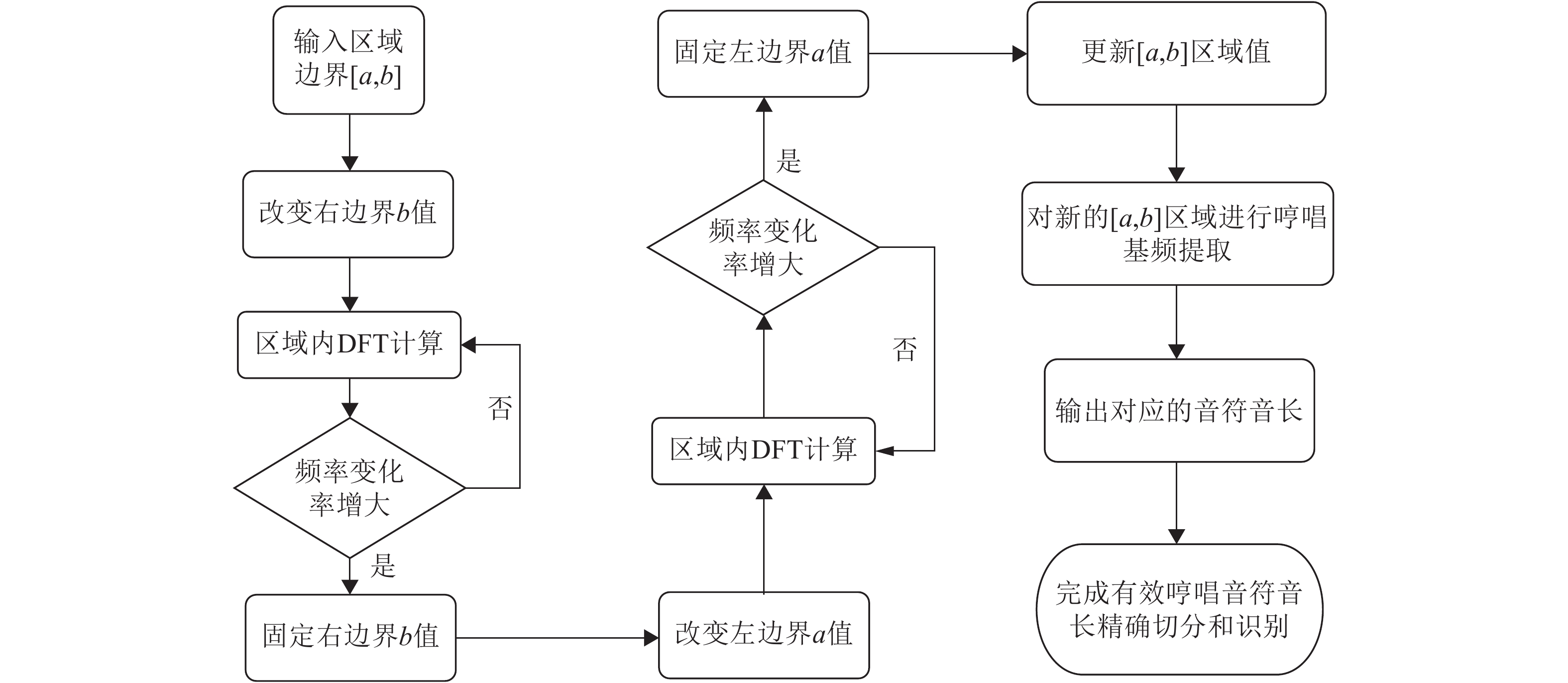
$\Delta {f_k}$ 为第k次边界改变时对应的基频变化率;${f_k}$ 为第k次边界改变后区域对应的基频;${P_{k + 1}}$ 为第k+1次边界改变的阻尼大小。在迭代过程中,若${P_{k + 1}}$ <0,则继续沿当前边界改变的方向迭代;若${P_{k + 1}}$ >0,则停止当前边界改变,迭代结束。算法流程见图4,具体步骤如下。
1)取2.2节中描述的有效音符音长区域
${{\rm {Len}}_k}$ ,定义[a,b]区间对应音频相应的振幅范围,a为振幅矩阵F中的一个起始序号,相当于一个起始采样点,b为振幅矩阵中一个终止的序号,由a、b的值决定所选择区域的长度。2)逐次改变右边界,即b的值。在[a,b]区域内进行哼唱基频提取通过迭代判断频率的变化,计算频率变化最小值,记录对应的b值。
3)改变左边界,即a的值,同样进行哼唱基频提取并计算频率变化最小值对应的a值,迭代完毕后记录a、b的值,确定最终区域。
4)对最终区域[a,b]进行处理,对应的基频视为该音频率,根据式(6)计算其时长,记录为该哼唱的音符音长。
每处理完一个区域后,按照步骤1)~步骤4)进行下一个区域的精确识别,直到整个哼唱音频结束。通过变化阻尼
${P_k}$ 判定频率变化方向后,再计算基频变化率$\Delta {f_k}$ ,这样可以显著减少整个哼唱音频的迭代计算次数,提高效率。当精度在误差允许范围内,迭代步长应该尽量取长,但是这样会严重影响算法效率。对典型的人声哼唱曲调按照精确步长分别取5、10、15、20、25进行测试,输出不同的迭代终点对应区域基频的精度,发现迭代的步长将影响
$\Delta {f_k}$ 和${P_{k + 1}}$ 的大小,迭代步长越大,$\Delta {f_k}$ 普遍越大,${P_{k + 1}}$ 普遍越小,到达迭代终点所需的迭代次数越少,由此所确定的区域对应基频的精确度越低。根据效率和精确度综合判断,在对大量音频进行分析后发现,当迭代步长增大到20时,偶尔会出现超过一个半音的误差,因此迭代步长应取15比较合适。3. 实验与结果分析
本文使用Python 3.6作为编程语言[15],应用Python提供的wave软件开发包,编程提取了哼唱录音成WAV文件格式音频信号,实现了对音频的通道数、量化位数、采样率(Fs)、采样点数(N)的矩阵计算与存储;采用了numpy软件开发包实现了快速傅里叶变换(FFT)[16]及相应的矩阵换算。
根据10个以确定的谱曲,分别进行人声哼唱录音,录音设备为普通智能手机,录音地点为校园宿舍,10个哼唱音频数据见表1,其中包含2个低音音阶、2个高音音阶、2个短时随意哼唱、2个长时随意哼唱、2个合成声。
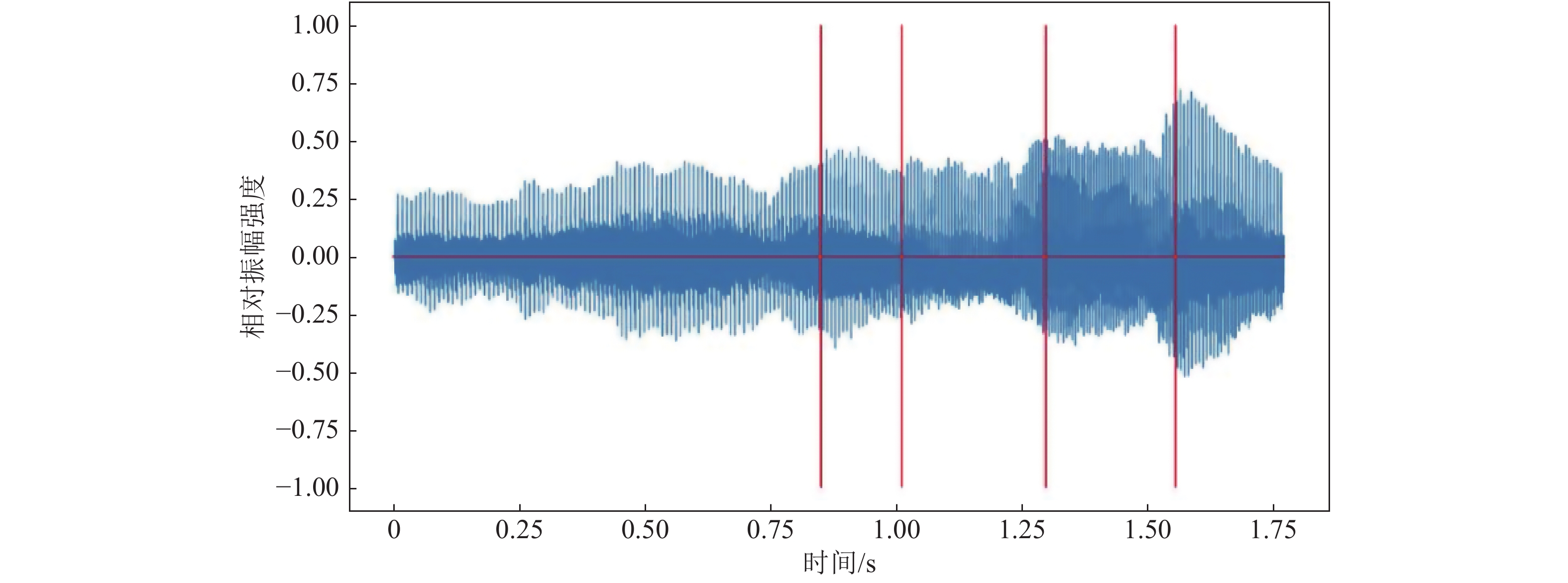
表 1 10个哼唱音频原始数据表数据名称 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 少音低音音阶 E3|1 F3|1 G3|1 A3|1 None None None None 多音低音音阶 C3|1 D3|1 E3|1 F3|1 G3|1 A4|1 B4|1 C4|1 少音高音音阶 B5|1 A5|1 G4|1 F4|2 None None None None 多音高音音阶 C4|1 D4|1 E4|1 F4|1 G4|1 A5|1 B5|1 C5|1 少音随意哼唱1 A3|3 B3|3 D3|1 F3|1 D3|1 None None None 少音随意哼唱2 A3|1 B3|1 D3|1 A3|1 None None None None 多音随意哼唱1 A5|1 G4|1 A5|1 C5|1 B5|1 A5|1 G4|1 None 多音随意哼唱2 B3|1 D3|1 A4|1 F3|1 E3|1 C3|1 D#3|1 E3|1 少音合成人声 F4|5 G4|2 F4|5 None None None None None 多音合成人声 G4|5 F4|1.5 D4|1 A5|2 G4|3.5 F4|1.5 C4|1 D4|3 由于篇幅有限,本文以少音随意哼唱1为例展示实验运行结果,所有实验结果均由Python 3.6语言编程运行后获得。对少音随意哼唱1的信息首先进行离散傅里叶变化提取基频,然后采用5 000帧长对其进行分帧,对每帧进行快速傅里叶变换得到的基频,结果如图5所示。少音随意哼唱1分帧为38帧,由基频和每帧的对应关系,计算出矩阵F与矩阵R(见图6),计算完成音符音长的切分。
对有效哼唱音符音长区域进行切分后,采用可变区域的加窗傅里叶精确识别迭代算法进一步进行最终时长划分,效果图见图7。按照音频识别流程(图2)和2.2、2.3节所述算法步骤运行,对表1中的录音音频依次处理,最后根据国际标准音高度量换算,输出结果如表2所示。
考虑人声本身发音可能存在误差,输出的音高差距在一个半音内视为正确音,差距在一个半音以上视为错音。对原有10个曲谱的音符、音高、音长进行了对比,正确率达到84.3%。分析误差来源有:1) 随意哼唱的音符音长本来就不存在精确的节拍规律,本身存在1~2拍的误差;2) 由于录音设备和录音场地简陋,多音随意哼唱录音效果较差;3) 该算法只统计了有效哼唱音符音长区域,这是一个频率较为稳定的区域,而没有统计2个音之间频率变化的非稳定区域,可能出现遗漏。但该方法总体正确率高,达到满意结果,表明该算法具有一定的普适性,具有较好的应用价值。
表 2 10个哼唱音频识别输出记谱表数据名称 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 少音低音音阶 E3|4 F3|2 F3|4 A4|3 None None None None 多音低音音阶 C3|1 C3|2 D3|4 F3|4 G3|1 C#3|4 Bb4|1 B4|4 少音高音音阶 B5|2 Bb5|2 G#4|3 E4|8 None None None None 多音高音音阶 G3|5 D4|5 E4|5 F#4|2 G4|2 G#4|2 A5|4 C5|6 少音随意哼唱1 A3|9 B3|2 C#3|3 E3|3 C#3|3 None None None 少音随意哼唱2 A4|2 C3|7 D3|4 A4|6 None None None None 多音随意哼唱1 A5|2 F#4|2 F#4|2 A5|3 B5|5 G#4|3 G4|3 None 多音随意哼唱2 B3|3 C3|2 D3|6 E3|3 D3|3 C#3|5 C#3|3 Eb3|3 少音合成人声 F4|7 G4|2 F4|9 None None None None None 多音合成人声 G4|5 Eb4|2 Bb5|1 G4|2 F4|3 C4|1 Eb4|1 Eb4|1 4. 结 束 语
在对人声哼唱特征进行分析的基础上,通过对大量离散数字哼唱音频进行分析,给出了以相对振幅为依据的直接提取基频方法,并提出了基频修正公式。结合哼唱特征和加窗傅里叶变换分帧处理技术,建立了频率矩阵和节拍矩阵,实现了有效哼唱音符音长区域切分。设计并实现了一种可变识别区域的精确识别迭代算法,通过引入频率变化率
$\Delta {f_k}$ 和变化阻尼${P_k}$ 判定方法,显著减少整个哼唱音频的迭代次数,在Python 3.6编程环境下,经过反复测试与应用,对人声平常哼唱音高音长识别准确率达到了84.3%。 -
表 1 10个哼唱音频原始数据表
数据名称 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 少音低音音阶 E3|1 F3|1 G3|1 A3|1 None None None None 多音低音音阶 C3|1 D3|1 E3|1 F3|1 G3|1 A4|1 B4|1 C4|1 少音高音音阶 B5|1 A5|1 G4|1 F4|2 None None None None 多音高音音阶 C4|1 D4|1 E4|1 F4|1 G4|1 A5|1 B5|1 C5|1 少音随意哼唱1 A3|3 B3|3 D3|1 F3|1 D3|1 None None None 少音随意哼唱2 A3|1 B3|1 D3|1 A3|1 None None None None 多音随意哼唱1 A5|1 G4|1 A5|1 C5|1 B5|1 A5|1 G4|1 None 多音随意哼唱2 B3|1 D3|1 A4|1 F3|1 E3|1 C3|1 D#3|1 E3|1 少音合成人声 F4|5 G4|2 F4|5 None None None None None 多音合成人声 G4|5 F4|1.5 D4|1 A5|2 G4|3.5 F4|1.5 C4|1 D4|3 表 2 10个哼唱音频识别输出记谱表
数据名称 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 音名|时长/拍 少音低音音阶 E3|4 F3|2 F3|4 A4|3 None None None None 多音低音音阶 C3|1 C3|2 D3|4 F3|4 G3|1 C#3|4 Bb4|1 B4|4 少音高音音阶 B5|2 Bb5|2 G#4|3 E4|8 None None None None 多音高音音阶 G3|5 D4|5 E4|5 F#4|2 G4|2 G#4|2 A5|4 C5|6 少音随意哼唱1 A3|9 B3|2 C#3|3 E3|3 C#3|3 None None None 少音随意哼唱2 A4|2 C3|7 D3|4 A4|6 None None None None 多音随意哼唱1 A5|2 F#4|2 F#4|2 A5|3 B5|5 G#4|3 G4|3 None 多音随意哼唱2 B3|3 C3|2 D3|6 E3|3 D3|3 C#3|5 C#3|3 Eb3|3 少音合成人声 F4|7 G4|2 F4|9 None None None None None 多音合成人声 G4|5 Eb4|2 Bb5|1 G4|2 F4|3 C4|1 Eb4|1 Eb4|1 -
[1] 佟雪娜, 朗云迪. 中国数字音乐产业发展报告[C]//两岸创意经济研究报告. 北京: 社会科学文献出版社, 2017: 49-67. TONG Xue-na, LANG Yun-di. China digital music industry development report[C]//Cross-Strait Creative Economy Research Report. Beijing: Social Science Literature Press, 2017: 49-67.
[2] 周泉. 简介歌曲写作的方法[J]. 科教文汇, 2009(4): 270. DOI: 10.3969/j.issn.1672-7894.2009.04.221 ZHOU Quan. A brief introduction to the method of song writing[J]. The Science Education Article Collects, 2009(4): 270. DOI: 10.3969/j.issn.1672-7894.2009.04.221
[3] 张杰, 龙子夜, 张博, 等. 语音信号处理中基频提取算法综述[J]. 电子科技大学学报, 2010(s1): 99-102. ZHANG Jie, LONG zhi-ye, ZHANG Bo, et al. Summary of fundamental frequency extraction algorithms in speech signal processing[J]. Journal of University of Electronic Science and Technology of China, 2010(s1): 99-102.
[4] 秦静. 基于内容和语义的音乐检索技术研究与应用[D]. 大连: 大连理工大学, 2018. QIN Jing. Research and application of music retrieval technology based on content and semantics[D]. Dalian: Dalian University of Technology, 2018.
[5] KWOK H K, JONES D L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform[J]. IEEE Transactions on Signal Processing, 1995, 48(10): 2964-2972.
[6] DRESSLER K. Sinusoidal extraction using an efficient implementation of a multi-resolution FFT[C]//Proc of the Int Conf on Digital Audio Effects DAFx. Montréal: McGill University, 2006: 247-252.
[7] 鲁佳. 用于哼唱的音乐检索技术研究与实现[D]. 上海: 上海海事大学, 2007. LU Jia. Research and implementation of music retrieval technology for humming[D]. Shanghai: Shanghai Maritime University, 2007.
[8] 张文歆. 基于多基频提取的歌曲主旋律提取研究[D]. 北京: 北京邮电大学, 2014. ZHANG Wen-xin. Extraction of the main melody of a song based on multi-fundamental frequency extraction[D]. Beijing: Beijing University of Posts and Telecommunications, 2014.
[9] HERMES D J. Measurement of pitch by subharmonic summation[J]. Journal of the Acoustical Society of America, 1988, 83(1): 257-264. DOI: 10.1121/1.396427
[10] CAO C, LI M, LIU J, et al. Singing melody extraction in polyphonic music by harmonic tracking[C]//International Conference on Music Information Retrieval, Ismir 2007. Vienna, Austria: DBLP, 2008: 373-374.
[11] 徐坤玉, 张彩珍, 药雪崧. 语音信号的加窗傅里叶变换研究[J]. 山西师范大学学报(自然科学版), 2011, 25(3): 79-82. DOI: 10.3969/j.issn.1009-4490.2011.03.020 XU Kun-yu, ZHANG Cai-zhen, YAO Xue-jing. Research on windowed Fourier transform of speech signals[J]. Journal of Shanxi Normal University(Natural Science Edition), 2011, 25(3): 79-82. DOI: 10.3969/j.issn.1009-4490.2011.03.020
[12] 汪伟, 谢皓臣, 梁光明, 等. 加窗离散傅里叶变换性能分析和比对[J]. 现代电子技术, 2012, 35(3): 115-118. DOI: 10.3969/j.issn.1004-373X.2012.03.032 WANG Wei, XIE Hao-chen, LIANG Guang-ming, et al. Performance analysis and comparison of windowed discrete Fourier transform[J]. Modern Electronics Technique, 2012, 35(3): 115-118. DOI: 10.3969/j.issn.1004-373X.2012.03.032
[13] GABOR D. Theory of communication[J]. J Inst Electr Eng, 1946, 93: 429-457.
[14] 王恩成, 苏腾芳, 袁开国, 等. 哼唱检索中联合音高与能量的音符切分算法[J]. 计算机工程, 2012, 38(9): 4-7. DOI: 10.3969/j.issn.1000-3428.2012.09.002 WANG En-cheng, SU Teng-fang, YUAN Kai-guo, et al. Symbol segmentation algorithm combining pitch and energy in humming retrieval[J]. Computer Engineering, 2012, 38(9): 4-7. DOI: 10.3969/j.issn.1000-3428.2012.09.002
[15] Python Software Foundation. The python standard library[EB/OL]. [2018-08-16]. https://docs.python.org/3.6/library.
[16] 杨丽娟, 张白桦, 叶旭桢. 快速傅里叶变换FFT及其应用[J]. 光电工程, 2004, 31(b12): 1-3. YANG Li-juan, ZHANG Bai-hua, YE Xu-zhen. Fast fourier transform FFT and its application[J]. Opto-Electronic Engineering, 2004, 31(b12): 1-3.
-
期刊类型引用(4)
1. 万凌艳. 基于双重消噪的钢琴音频信号特征自动识别方法. 自动化与仪器仪表. 2022(01): 35-38 .  百度学术
百度学术
2. 范静. 考虑音符序列的钢琴演奏和弦指法自动标注算法. 常州工学院学报. 2022(05): 39-45 .  百度学术
百度学术
3. 赵兴元. 机器学习在花儿识别中的运用. 信息与电脑(理论版). 2021(01): 145-147 .  百度学术
百度学术
4. 许丞. 基于卷积神经网络的钢琴音频信号识别算法. 自动化与仪器仪表. 2021(12): 12-15 .  百度学术
百度学术
其他类型引用(0)

 ISSN
ISSN 


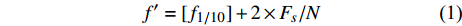
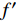
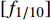
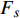
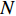
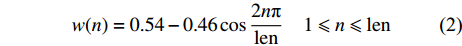
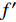
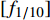
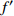
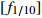
 下载:
下载: