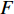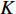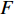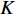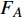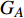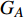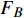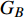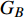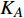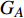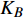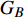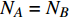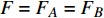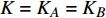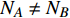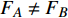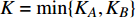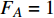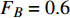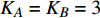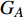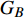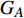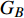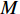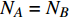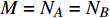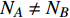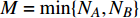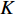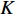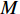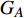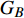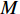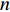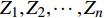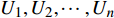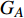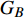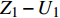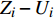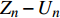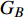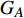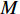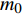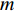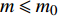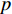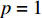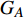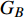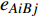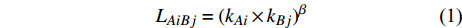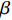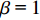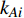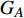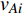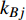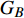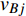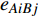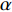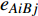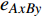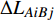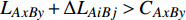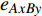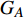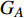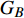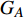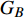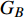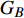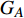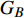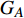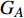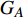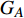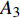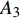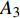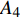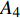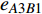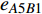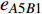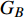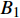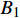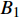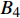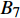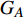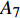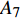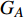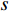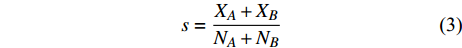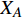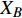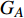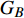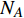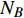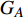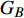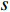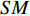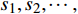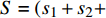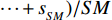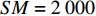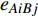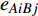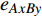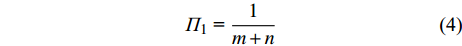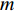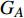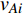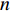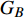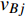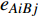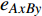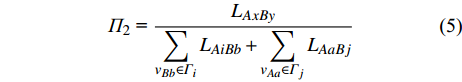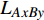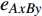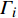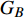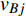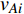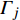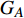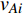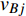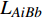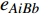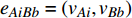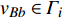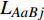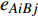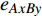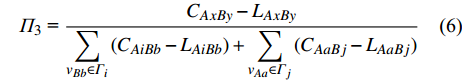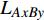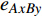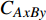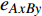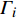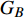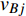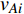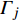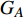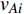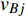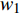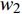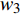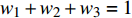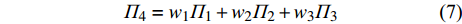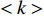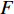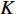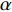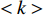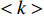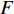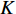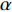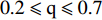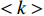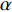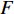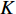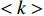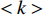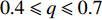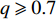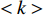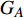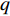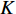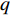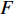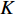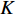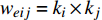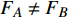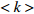Research on Robustness of Interdependent Networks Considering Dependent Side Load
-
摘要: 针对现实中不同网络之间的连接边存在负载传递和容量约束的现象,提出了一种考虑相依边负载的相依网络级联失效模型,并将该模型运用到地铁公交相依网络上,分析不同交通网络之间的换乘所带来的负载分配问题。该模型综合考虑了相依边过载失效、相依节点故障和非最大连通子图节点损失的失效情况。通过调节攻击比例,分析不同负载重分配策略、不同的网络耦合方式与组合模式、网络的相依程度、不同边攻击方式下对相依网络鲁棒性的影响。结果表明:剩余容量分配策略能有效缓解相依边的过载失效,小世界网络组成的相依网络鲁棒性更好;提高耦合程度和子网络的平均度能有效提高相依网络的抗毁性;相较于相连边,攻击相依边对网络的鲁棒性影响更大。Abstract: In view of the phenomenon of load transfer and capacity constraints in the connection edges between different networks in reality, a cascading failure model of interdependent networks considering dependent side loads is proposed and applied to the subway bus dependent networks to analyze the load distribution problem caused by the transfer between different transportation networks. In this model, the failure of dependent edge load, failure of dependent nodes and loss of non-maximum connected subgraph are comprehensively considered. By adjusting the attack ratio, this paper analyzes the influence of different load redistribution strategies, different network coupling modes and combination modes, the degree of network dependence and different edge attack modes on the robustness of interdependent networks. The results show that the residual capacity allocation strategy can effectively alleviate the overload failure of dependent edges, and the robustness of interdependent networks composed of small-world networks is better. The robustness of model decreases as the proportion of dependency node increases and increases as the redundancy of dependency increases. Improving the coupling degree and the average degree of sub-networks can effectively improve the invulnerability of interdependent networks. Compared with connected edges, attacking dependent edges has a greater impact on the robustness of networks.
-
Keywords:
- cascade failure /
- dependent edge /
- dependent network /
- load redistribution /
- robustness /
- subway and bus network
-
在现实世界中,存在着许多相互依赖的复杂网络,这些不同网络之间存在着紧密联系。当网络受到某些因素影响时,会对其他相关网络产生不同程度的危害,进而造成大规模损失。如2019年3月委内瑞拉电力系统遭遇多次攻击[1],国内大部分地区持续停电,电网故障导致交通堵塞、信息网络受阻;2020年新冠肺炎疫情在全球爆发[2],造成大规模传播,社会各个行业都受到严重影响;2021年3月“长赐”号在苏伊士运河搁浅[3],导致全球海运航道发生堵塞,对一些大宗商品市场、全球供应链和原材料价格带来了一系列影响。因此,研究此类相依网络之间的联系和鲁棒性具有重要的现实意义。
自2010年,文献[4]在《Nature》杂志上发表后,相依网络的应用与研究成为了国内外学者关注的热点。目前,相依网络失效模型在一系列基础设施网络中应用较为广泛,如文献[5]分析了在极端天气下,公交−地铁复杂双层网络的连锁故障和网络系统的脆弱性演化。文献[6]基于出行时间的可达性、出发的最佳可及性和往返行程的无障碍性3种衡量行程时间的指标,来分析时变可访问性对地铁和高铁相依网络系统的影响。文献[7]先对电力信息物理相依系统进行建模,后深入分析了节点脆弱性新特性、线路耦合深度和信息失效对网络相变特性的影响。文献[8]构建了高铁−普铁交通双层复杂网络,并对子网络和相依网络的拓扑静态指标进行了分析。而文献[9-10]分别在随机攻击和蓄意攻击的基础上,提出了一种考虑破坏力随距离衰减的局部攻击模式和多种攻击方式组合下的联合攻击策略。文献[11-12]分别提出局部优化NPC(邻居节点优先连接)的耦合策略和基于重叠链路结构的相互依赖网络耦合策略,这些耦合策略相较于传统的随机、同配和异配耦合模式能更有效地增强网络系统的鲁棒性。文献[13]在渗流理论的基础上提出了级联故障渗流模型,并分析了相依网络的耦合强度对网络相变特性的影响。文献[14-15]基于负载局域分配原则提出了负载级联失效模型,引入了节点负荷过载的失效情况,并研究了具有不同攻击策略、连接模式和负载分配机制的相互依赖网络的鲁棒性。文献[16]提出一种新的基于社区结构的容量分配策略,在不改变网络结构的情况下,这种策略能有效减少级联故障,提高网络鲁棒性。文献[17]提出了一个基于负载波动下相互流量重新分配的依赖网络级联失效模型,并通过流量损失参数来分析网络现有资源的流量损耗。但这些研究的负载级联失效模型集中于分析网络内的节点和连边,忽视了网络间的相依边同样具有负荷流动的现象。文献[18]通过建立对称相依网络和不对称相依网络模型,对负载最大的子网络相连边和相依边分别进行失效,对比网络相连边和相依边对相依网络临界成本的贡献,然而文献中并未考虑现实相依网络中相连边和相依边负载所指代的物理意义并不相同,网络内的负载在进行负载重分配时一般不进行跨网络传输。
通过对上述文献的梳理,发现多数文献的研究并没有考虑子网络之间相依边的负载,现实中不但网络内部存在负载,而且不同网络之间的信息传递也具有负荷流动的现象。相依网络中的相依边不但具备逻辑上的相依关系,也存在功能上的实际负载量。如电力网络与交通网络之间存在具体信息的传递,这些信息也受负荷流动和容量限制的约束;在不同的交通网络间存在换乘问题,公交网络站台和地铁网络站点之间的换乘路线可视作网络间的相依边,换乘的人数为相依边上的负载量,而恶劣天气造成的部分路面积水和道路维修导致的局部封路等情况都会使乘客换乘不便,不得不改换邻近站点进行换乘。
本文在这些研究的基础上,提出了考虑相依边负载的相依网络级联失效模型,并定义相依边的初始负载和初始容量,失效情况综合考虑了相依边过载失效、相依节点故障和非最大连通子图损失。以2021年6月南昌地铁网络(http://www.ncmtr.com)和部分公交网络(https://nanchang.8684.cn)组成的相依网络作为模型的实际用例,对模型的物理意义和合理性进一步说明。另外本文对考虑相依边负载的相依网络进行了多角度的分析,为进一步改善相依网络的级联失效提供新的途径。
1. 考虑相依边负载的相依网络级联失效模型
1.1 相依网络拓扑结构与性质分析
本文的相依网络系统由独立的两个子网络构成,分别为子网络
$ {G_A} $ 和子网络$ {G_B} $ ,而且节点总数为$ N = {N_A} + {N_B} $ ,它们都有特定的网络拓扑结构,并通过一定的方式进行连接。其中子网络中内部节点连接的边定义为相连边,子网络$ {G_A} $ 和$ {G_B} $ 之间节点连接的边定义为相依边。网络系统中的子网络以
$ {G_A} $ 网络为例,它的简单系统图可以表示为$ {G_A} = [{V_A},{E_A}] $ ,其中$ {V_A} = \{ {v_{Ai}}|i = 1,2, \cdots ,{N_A}\} $ 表示相依网络中子网络$ {G_A} $ 的节点集,$ {E_A} = \{ {e_{Aij}}|{e_{Aij}} = ({v_{Ai}},{v_{Aj}}),i = 1, $ $ 2, \cdots ,{N_A}; j = 1,2, \cdots , {N_A};i \ne j\} $ 代表了子网络$ {G_A} $ 中节点之间相连边的边集,$ {e_{Aij}} $ 表示子网络$ {G_A} $ 中节点$ {v_{Ai}} $ 与节点$ {v_{Aj}} $ 相连,同理子网络$ {G_B} $ 也具有相类似的系统图表示。在相依网络中将相依边的边集定义为
${E_{AB}} = $ {$ {e_{AiBj}}|{e_{AiBj}} = ({v_{Ai}},{v_{Bj}}),i = 1,2, \cdots ,{N_A};j = 1, $ $ 2,\cdots ,{N}_{B} $ ; i和j可以相等},当$ {e_{AiBj}} = 1 $ 表示子网络$ {G_A} $ 中的节点$ {v_{Ai}} $ 与子网络$ {G_B} $ 中的节点$ {v_{Bj}} $ 连接,即子网络$ {G_A} $ 中节点$ {v_{Ai}} $ 与子网络$ {G_B} $ 中节点$ {v_{Bj}} $ 具有相依关系,反之则$ {e_{AiBj}} = 0 $ 。为方便研究相依边的负载分配,本文定义一个新的参数:邻近相依边集,某相依边
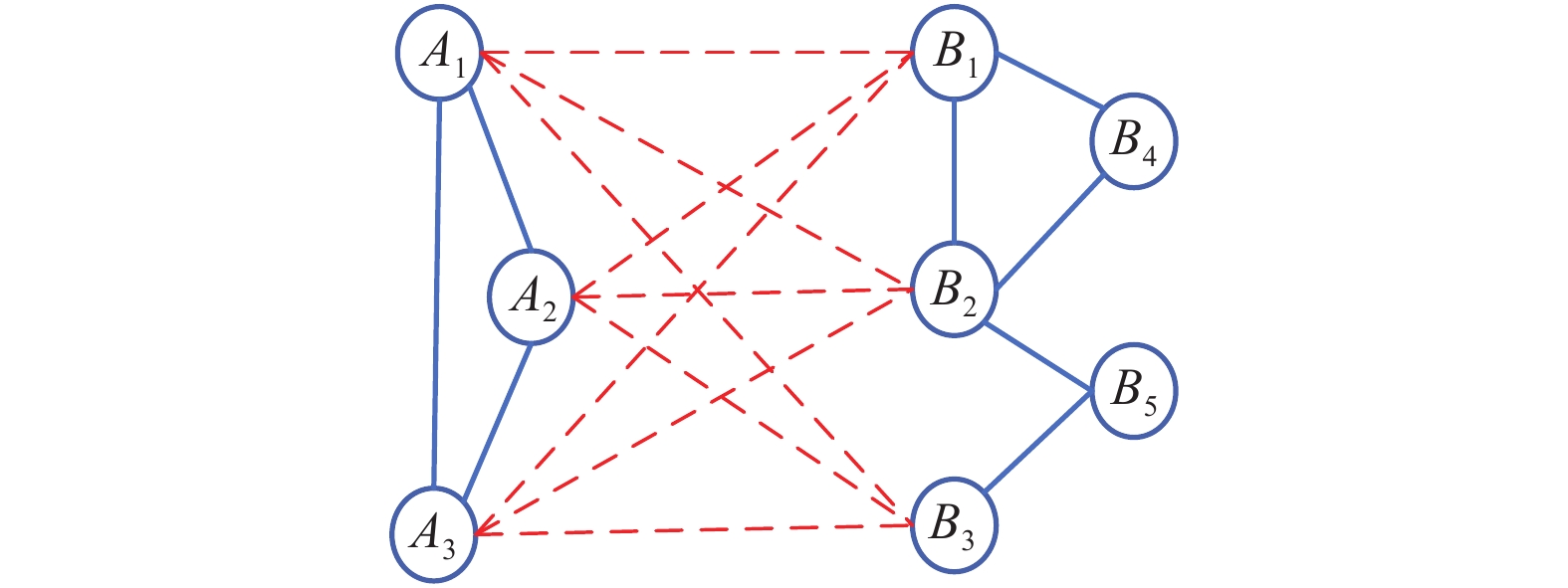
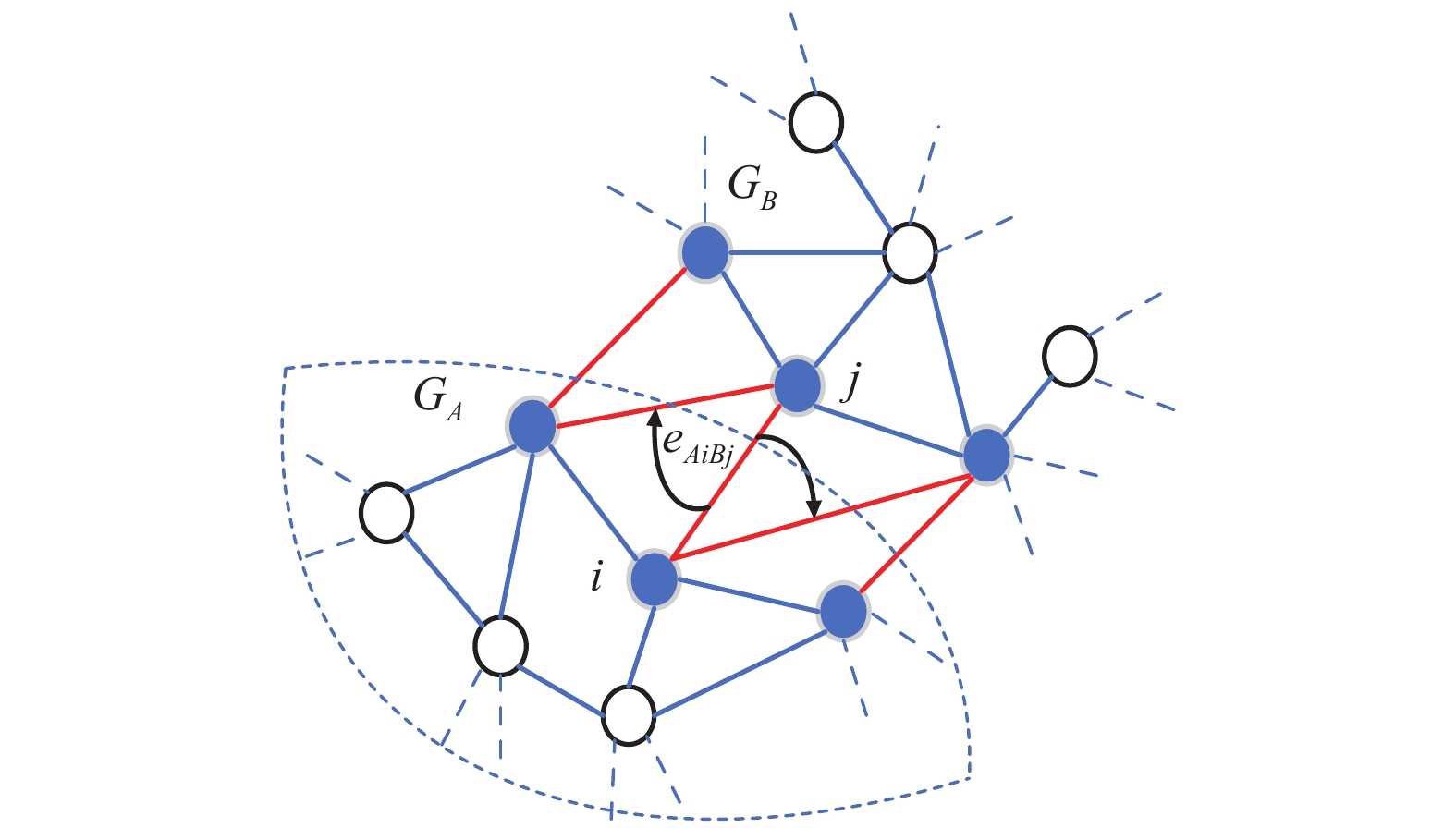
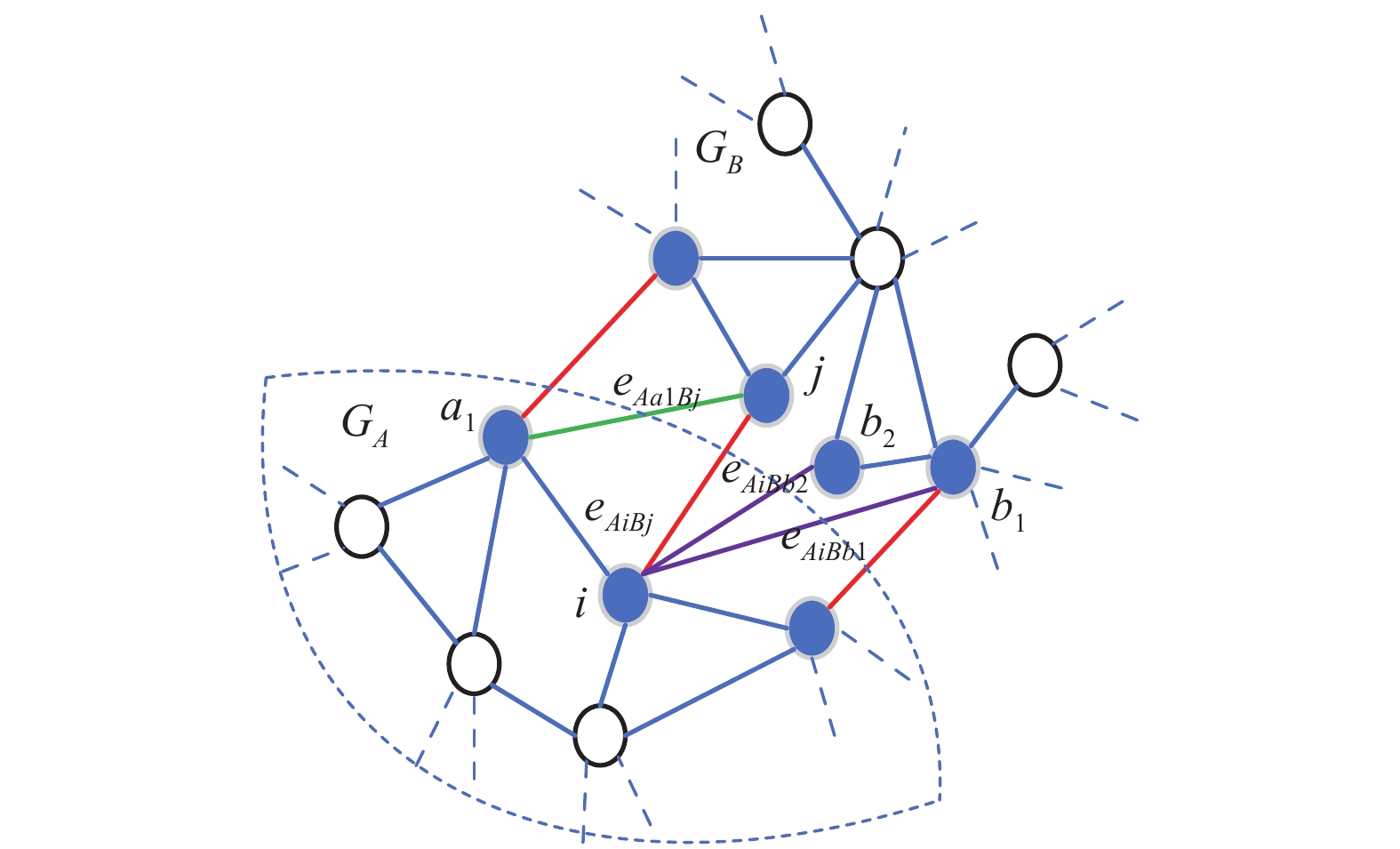
$ {e_{AiBj}} $ 的邻近相依边集可表示为$ {\rm{EL}} = {\rm{E}}{{\rm{L}}_A} \cup {\rm{E}}{{\rm{L}}_B} $ ,其中${\rm{E}}{\rm{{L}}_A} = \{ {e_{AiBb}} = ({v_{Ai}},{v_{Bb}})|{v_{Bb}} \in {\varGamma _i}\}$ ,$ {\rm{E}}{{\rm{L}}_B} = \{ {e_{AaBj}} $ $= ({v_{Aa}},{v_{Bj}})|{v_{Aa}} \in {\varGamma _j}\}$ ,${\varGamma _i}$ 表示子网络$ {G_B} $ 中除节点$ {v_{Bj}} $ 以外与节点$ {v_{Ai}} $ 相连的节点集合,${\varGamma _j}$ 表示子网络$ {G_A} $ 中除节点$ {v_{Ai}} $ 以外与节点$ {v_{Bj}} $ 相连的节点集合,${\varGamma _i}$ 和${\varGamma _j}$ 为点集。邻近相依边集如图1所示,设某相依边为$ {e_{AiBj}} $ ,那么它的邻近相依边集$ {\rm{EL}} $ 有$ {e_{Aa1Bj}} $ 、$ {e_{AiBb1}} $ 和$ {e_{AiBb2}} $ 。上式中${\varGamma _i} = \{ {v_{Bb1}},{v_{Bb2}}\}$ ,${\varGamma _j} = \{ {v_{Aa1}}\}$ ,$ {\rm{E}}{{\rm{L}}_A} $ =$ \{ {e_{AiBb1}},{e_{AiBb2}}\} $ ,$ {\rm{E}}{{\rm{L}}_B} $ =$ \{ {e_{Aa1Bj}}\} $ ,$ {\rm{EL}} = {\rm{E}}{{\rm{L}}_A} \cup {\rm{E}}{{\rm{L}}_B} = \{ {e_{Aa1Bj}},{e_{AiBb1}},{e_{AiBb2}}\} $ 。为进一步分析文中所提出的考虑相依边负载的相依网络的相依程度和耦合模式,沿用文献[19]定义的两个参数
$ F $ 和$ K $ ,$ F $ 为相依节点的比例,$ K $ 为相依冗余度。$ {F_A} $ 表示子网络$ {G_A} $ 的相依节点数占子网络$ {G_A} $ 节点总数的比例,$ {F_B} $ 表示子网络$ {G_B} $ 的相依节点数占子网络$ {G_B} $ 节点总数的比例;而$ {K_A} $ 为在子网络$ {G_A} $ 中相依节点的平均相依边数,$ {K_B} $ 为在子网络$ {G_B} $ 中相依节点的平均相依边数。本文定义相依网络为对称相依网络时,$ {N_A} = {N_B} $ ,$ F = {F_A} = {F_B} $ ,即两个子网络具有相同的网络规模和相依节点比例,且$ K = {K_A} = {K_B} $ ;若为不对称相依网络时,即$ {N_A} \ne {N_B} $ ,$ {F_A} \ne {F_B} $ 时,此时$ K = \min \{ {K_A},{K_B}\} $ 。如在图2中,$ {F_A} = 1 $ ,$ {F_B} = 0.6 $ ,$ {K_A} = {K_B} = 3 $ 。同时网络之间的耦合关系以节点的度值为标准,子网络
$ {G_A} $ 与$ {G_B} $ 之间有同配耦合、异配耦合和随机耦合3种不同的耦合模式。其中同配耦合是先对子网络$ {G_A} $ 与子网络$ {G_B} $ 中的节点分别按节点度值的降序排列,再将节点进行配对连接,连接的具体步骤为先将每个子网络中降序排列好的前$ M $ 个节点进行分组(当$ {N_A} = {N_B} $ 时,$ M = {N_A} = {N_B} $ ;当$ {N_A} \ne {N_B} $ 时,$ M = \min \{ {N_A},{N_B}\} $ ),以$ K $ 个节点为一个单元组(其中$ K $ 为相依网络的相依冗余度,当$ M $ 个节点无法被相依冗余度$ K $ 整除时,则剩余的余数单独组成最后一组)。假设子网络$ {G_A} $ 和$ {G_B} $ 中前$ M $ 个节点被分为$ n $ 组:${Z_1},{Z_2}, \cdots ,{Z_n}$ 和${U_1},{U_2}, \cdots ,{U_n}$ ,将子网络$ {G_A} $ 中第一组的每个节点与子网络$ {G_B} $ 中第一组的所有节点进行连接,即$ {Z_1} - {U_1} $ ,并以此类推使得$ {Z_i} - {U_i} $ ,最终$ {Z_n} - {U_n} $ 。同理可知,异配耦合则将子网络$ {G_B} $ 中的节点按度值的升序排列,将子网络$ {G_A} $ 中的节点按度值降序排列,具体连接方式与同配一致;随机耦合则对每个子网络随机选取$ M $ 个节点进行分组,具体连接方式与异配相同。在子网络的选取时,本文采用3种经典的人工网络模型作为相依网络的子网络。其中BA(Barabási-Albert)无标度网络模型的具体构建算法是先在给定初始节点
$ {m_0} $ 的情况下,每一步都添加一个新的节点,然后将新节点与$ m $ 个已存在的节点进行相连,且规定$ m \leqslant {m_0} $ ,相连方式按择优连接的概率进行连接[20]。WS(Watts-Strogatz)小世界网络模型的构造算法是先从规则网络开始,再进行随机化重连,即将网络中的每条边以概率$ p $ 进行重连[21]。ER(Erdős-Rényi)网络模型构建方法是以WS网络模型为基础的,不同点在于重新布线的概率$ p = 1 $ [22]。本文中这3种经典网络的节点数都选择200个节点。将2021年6月南昌地铁与部分公交网络系统作为模型的应用实例,地铁公交网络是由3条地铁线路与40条客流量最大的市区公交线路组成。由3条地铁线路组成的地铁网络共有70个站点,而由40条市区公交线路组成的公交网络共有511个公交站点。将站点抽象为网络节点,相同交通工具的站点间的连接线路看作相连边,不同交通工具站点之间可换乘的线路为相依边,可换乘的条件设为地铁站点和公交站点之间距离在800 m以内,换乘的人数抽象为相依边的负载。若在换乘时遇到不可避免的因素,乘客不得不改换邻近站点进行换乘,如何优化分配改换站点的人数以使得换乘线路不会因为换乘人数太多而导致拥堵和滞留,这一问题可看作考虑相依边负载的相依网络级联失效模型的实际应用之一。将市区公交网络设为子网络
$ {G_A} $ ,地铁网络为子网络$ {G_B} $ ,此相依网络的相关参数如表1所示。表 1 2021年6月南昌地铁与部分公交网络的相关参数网络 节点数/个 相连边数/条 相依边数/条 平均度$ \lt k \gt $ 地铁网络 70 71 393 1.014 3 市区公交网络 511 649 393 1.270 1 1.2 相依边负载容量模型
在ML模型的基础上[23],本文提出了一种考虑相依边的负载容量模型,相依边
$ {e_{AiBj}} $ 的初始负载表示为:$$ {L_{AiBj}} = {({k_{Ai}} \times {k_{Bj}})^\beta } $$ (1) 式中,
$ \beta $ 为可调参数,控制相依边的初始负载,本文设定$ \beta {\text{ = }}1 $ ;$ {k_{Ai}} $ 表示子网络$ {G_A} $ 中节点$ {v_{Ai}} $ 的度值;$ {k_{Bj}} $ 表示子网络$ {G_B} $ 中节点$ {v_{Bj}} $ 的度值。相依边的初始容量与初始负载成正比,即相依边
$ {e_{AiBj}} $ 的初始容量可以表示为:$$ {C_{AiBj}} = (1 + \alpha ){L_{AiBj}} $$ (2) 式中,
$ \alpha $ 为可调参数,一般$ \alpha \geqslant 0 $ ,表示相依边的冗余程度即容忍系数,控制相依边的容量阈值。基于相依边的负载重分配规则,假设相依边
$ {e_{AiBj}} $ 失效时,邻近相依边$ {e_{AxBy}} $ 以一定的分配比例获得额外的负载$ \Delta {L_{AiBj}} $ ,当$ {L_{AxBy}} + \Delta {L_{AiBj}} \gt {C_{AxBy}} $ 时,邻近相依边$ {e_{AxBy}} $ 过载失效,网络继续对失效的相依边进行负载分配,直到任意相依边的容量大于负载时,网络间相依边的负载失效才停止。相依边的负载重分配示意图如图3所示。1.3 级联失效模型的构建
本文的级联失效模型中失效具体情况一般分为以下4种,并且任意一种攻击和故障导致的节点失效,其对应的所有边也会被清除:
1) 在初始状态下外部攻击导致的初始失效可分为3种,其中任意一种攻击方式都可以引发网络的初始失效。
① 外部直接攻击节点导致的节点失效。
② 外界进攻网络内的相连边,以至于节点失去所有相连边,则该节点故障并被移除。
③ 外部袭击网络间的相依边,致使相依节点失去所有相依边,此相依节点失去了所有与另一个子网络耦合链接的物理通道,相对应的信息或负荷无法通过该相依节点进行跨网络传输,故视该节点失效。
2) 基于渗流理论的级联故障渗流模型[19],在子网络中若某一节点脱离了最大连通子图,则该节点失效[24]。
3) 在级联失效过程中,若节点为相依节点,由于失去了所有的相依边,该相依节点与另一个子网络的依存关系消失,相依节点与另一子网络间的正常联系中断,此相依节点失效[25]。
4) 基于上文中的相依边负载容量模型,当网络间的相依边失效时,会将失效相依边上的负载以一定比例分配给邻近相依边,若负载超过容量则发生过载失效,继续导致邻近相依边集的故障。在地铁公交网络中,假设在理想状态下换乘线路上的换乘人数超出额定的容量时,换乘线路失去基本换乘功能。根据以上4种失效模式,制定了模拟考虑相依边负载的级联失效模型的详细步骤如下。
① 对子网络
$ {G_A} $ 进行初始攻击,移除被攻击的节点与连边。② 子网络
$ {G_A} $ 分裂成若干个子图和孤立节点。基于渗流理论,当节点移除比例超过临界相变点,子网络被分解成多块互相不连通的集团。在网络中只有最大连通片保持基本的功能和相对的全局连通性,由于其余子图中的节点和孤立节点在结构上与最大连通子图并不连通,故可视为故障节点[4]。③ 子网络
$ {G_A} $ 内节点的移除,导致大量相依边失效。根据相依边负载容量模型,失效的相依边对邻近相依边集分配额外的负载,当邻近相依边的总负载量超过容量限制时会导致过载失效。④ 相依边的过载失效和子网络
$ {G_A} $ 内节点的移除使得子网络$ {G_B} $ 内相依节点失去大量的相依边,子网络$ {G_A} $ 的故障经过相依边负载重分配后传播到子网络$ {G_B} $ 。在子网络$ {G_B} $ 中,那些失去所有相依边的节点失效。⑤ 基于级联故障渗流模型,子网络
$ {G_B} $ 内发生步骤②中相似的非最大连通子图失效。若此时整个系统达到稳定状态,则失效结束,反之则将故障传播到子网络$ {G_A} $ 继续步骤⑥,如此反复迭代直到系统达到稳定。⑥ 子网络
$ {G_B} $ 内的失效会同样影响网络间的相依边,网络间的相依边会发生步骤③中的相依边过载失效。⑦ 相依边的过载失效会使得大量相依边被移除,进而导致子网络
$ {G_A} $ 发生相依失效,故障又传播回子网络$ {G_A} $ 。⑧ 系统的故障经过相依边的传递,再次回到子网络
$ {G_A} $ 中,重复步骤②~⑦,直到系统达到稳定。图4展示了一个简易相依网络的级联失效过程,在相依网络的初始状态(如阶段1)下,先蓄意攻击子网络
$ {G_A} $ 中的节点$ {A_3} $ ,则节点$ {A_3} $ 和它的连边(包括相连边和相依边)都失效,节点$ {A_3} $ 的失效导致节点$ {A_4} $ 脱离最大连通子图,则节点$ {A_4} $ 发生非最大连通子图失效。相依边$ {e_{A3B1}} $ 的失效,使得相依边发生负载重分配,若邻近相依边$ {e_{A5B1}} $ 获得额外负载后其总负载超过容量,则发生过载失效,继续进行负载分配。相依边$ {e_{A5B1}} $ 的邻近相依边获得额外负载,若相依边的总负载小于容量,则停止负载分配。又因为子网络$ {G_B} $ 中节点$ {B_1} $ 的相依边都被删除,节点$ {B_1} $ 失效被移除,并且节点$ {B_1} $ 的移除导致节点$ {B_4} $ 和$ {B_7} $ 脱离最大连通子图,故而同样发生节点失效,这些失效节点对应的连边也被移除。在阶段1中失效结束后,网络的状态如图4b所示,此时子网络$ {G_A} $ 中节点$ {A_7} $ 的所有相依节点失效,故而导致节点$ {A_7} $ 发生相依失效。此时系统中节点不再发生失效,相依网络达到稳定而且整个系统的状态如图4c所示。1.4 网络鲁棒性测量指标
攻击一定比例的节点后(若未特别说明,则是随机攻击子网络
$ {G_A} $ 的节点),考虑相依边负载的相依网络模型会发生级联失效。当网络级联失效达到稳定时,剩余最大连通子图中有效节点数与初始状态下子网络的节点总数的比例为鲁棒性指标,本文定义$ s $ 为相依网络的鲁棒性测量指标,表示为:$$ s = \frac{{{X_A} + {X_B}}}{{{N_A} + {N_B}}} $$ (3) 式中,
$ {X_A} $ 、$ {X_B} $ 分别为子网络$ {G_A} $ 和子网络$ {G_B} $ 中幸存最大连通子图中的有效节点;$ {N_A} $ 、$ {N_B} $ 分别为子网络$ {G_A} $ 和子网络$ {G_B} $ 中初始状态下节点的总数。显然$ s $ 值越大,相依网络的有效节点越多,整个网络系统的鲁棒性就越好。为了避免随机因素对整体仿真效果的影响,本文随机仿真生成
$ S M $ 个相依网络,并在相同的规则运行下得到一组鲁棒性测量指标分别为$ {s_1},{s_2}, \cdots , {s_{_{S M}}} $ 。对这组数据取均值$ S = ({s_1} + {s_2} + $ $ \cdots + {s_{_{S M}}})/S M $ 。本文仿真均取$ S M = 2\;000 $ 。2. 数值分析
2.1 相依边负载分配策略对网络鲁棒性的影响
在相依边负载分配时,相依边的负载重分配策略对网络的抗毁性有一定程度的影响,本文采用4种不同的负载重分配比例来对相依边过载失效进行分析。
1) 平均分配策略。当相依边
$ {e_{AiBj}} $ 失效且存在邻近相依边时,将相依边的负载平均分配给其所有邻近相依边。则相依边$ {e_{AiBj}} $ 分配给邻近相依边$ {e_{AxBy}} $ 的分配比例为:$$ {\varPi _1}{\text{ = }}\frac{1}{{m + n}} $$ (4) 式中,
$ m $ 表示子网络$ {G_A} $ 中节点$ {v_{Ai}} $ 上的相依边数;$ n $ 表示子网络$ {G_B} $ 中节点$ {v_{Bj}} $ 上的相依边数。2) 负载分配策略。由于负载反映了相依边上实际信息量,故对所有邻近相依边负载进行归一化,取其相对大小来作为分配比例。按失效相依边的邻近相依边负载比例进行重新分配,相依边
$ {e_{AiBj}} $ 分配给邻近相依边$ {e_{AxBy}} $ 的比例为:$$ {\varPi _2}{\text{ = }}\frac{{{L_{AxBy}}}}{{\displaystyle\sum\limits_{{v_{Bb}} \in {\varGamma _i}} {{L_{AiBb}} + \displaystyle\sum\limits_{{v_{Aa}} \in {\varGamma _j}} {{L_{AaBj}}} } }} $$ (5) 式中,
$ {L_{AxBy}} $ 为邻近相依边$ {e_{AxBy}} $ 的负载;$ {\varGamma _i} $ 表示子网络$ {G_B} $ 中除节点$ {v_{Bj}} $ 以外与节点$ {v_{Ai}} $ 相连的节点集合;$ {\varGamma _j} $ 表示子网络$ {G_A} $ 中除节点$ {v_{Ai}} $ 以外与节点$ {v_{Bj}} $ 相连的节点集合。其中$ {L_{AiBb}} $ 为求和内容,即求和的通项,表示$ {e_{AiBb}} $ 的负载,$ {e_{AiBb}} = ({v_{Ai}},{v_{Bb}}) $ ,求和的取值范围为$ {v_{Bb}} \in {\varGamma _i} $ ,同理$ {L_{AaBj}} $ 具有类似意义。3) 剩余容量分配策略。在级联失效的过程中,相依边所剩余的容量与其剩余可承受的负载成正比。所以相依边
$ {e_{AiBj}} $ 分配给邻近相依边$ {e_{AxBy}} $ 的比例为:$$ {\varPi _3}{\text{ = }}\frac{{{C_{AxBy}} - {L_{AxBy}}}}{{\displaystyle\sum\limits_{{v_{Bb}} \in {\varGamma _i}} {({C_{AiBb}} - {L_{AiBb}}) + \displaystyle\sum\limits_{{v_{Aa}} \in {\varGamma _j}} {({C_{AaBj}} - {L_{AaBj}})} } }} $$ (6) 式中,
$ {L_{AxBy}} $ 为邻近相依边$ {e_{AxBy}} $ 的负载;$ {C_{AxBy}} $ 为邻近相依边$ {e_{AxBy}} $ 的容量;$ {\varGamma _i} $ 表示子网络$ {G_B} $ 中除节点$ {v_{Bj}} $ 以外与节点$ {v_{Ai}} $ 相连的节点集合;$ {\varGamma _j} $ 表示子网络$ {G_A} $ 中除节点$ {v_{Ai}} $ 以外与节点$ {v_{Bj}} $ 相连的节点集合。4) 混合分配策略。将以上几种不同的重分配策略进行加权组合,则可得到混合分配策略。定义加权参数
$ {w_1} $ ,$ {w_2} $ ,$ {w_3} $ 且$ {w_1} + {w_2} + {w_3} = 1 $ ,则分配比例为:$$ {\varPi _4} = {w_1} {\varPi _1} + {w_2} {\varPi _2} + {w_3} {\varPi _3} $$ (7) 为研究相依边负载分配策略对网络鲁棒性的影响,将3种经典人工网络作为相依网络的子网络,子网络间采用随机耦合。令子网络的平均度
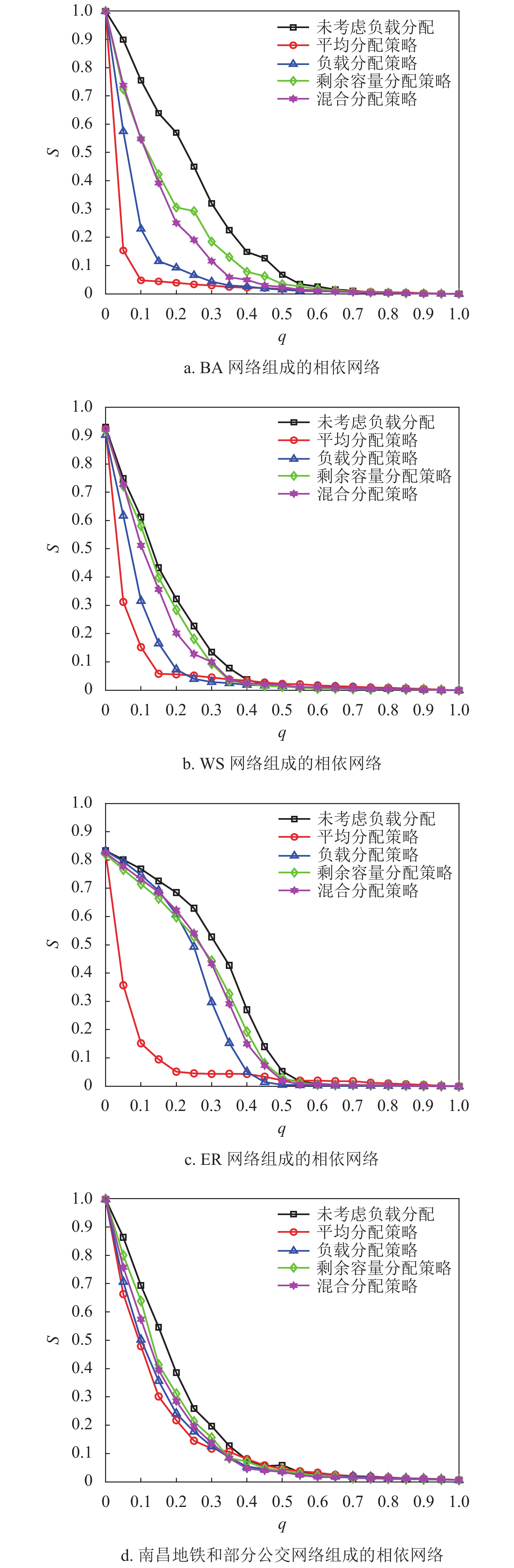
$ \lt k \gt $ =2,相依节点比例$ F $ =1,相依冗余度$ K $ =4,容忍系数$ \alpha $ =0.5,同时将南昌地铁和部分公交网络作为实验用例,探究不同的相依网络负载重分配策略对系统的鲁棒性影响,其仿真结果如图5所示。从图5可知,未考虑相依边负载分配策略时,系统的鲁棒性相对较好,因为此时系统仅考虑了拓扑结构对系统的影响,忽略了网络具有负荷流动的功能性特征,在结构特性的基础上考虑负载分配因素会增加网络故障的风险,但这也更符合现实要求。而平均分配策略在所有分配策略中表现最糟,剩余容量分配策略效果最好,负载分配策略和混合分配策略下的系统鲁棒性介于前两者之间。这是由于平均分配策略忽略了相依边的差异性,邻近相依边的剩余容量对接受额外负载的能力起很大作用。而剩余容量分配策略则是根据相依边的相对剩余容量进行分配,从而降低了相依边过载失效的风险。此外,混合分配策略不但考虑了相依边的剩余容量,而且考虑了失效相依边的邻近相依边总数,合理的对负载进行了分配。因此,混合分配策略相对较佳。另外南昌地铁和部分公交网络组成的相依网络与BA网络组成的相依网络仿真结果类似,整体下降的趋势相似,因为地铁和部分公交中网络的平均度约为为1,网络节点的度值分布较平均,而BA网络的节点度值分布较集中,所以BA网络组成的相依网络下降速度较快。在攻击比例为0时,WS网络组成的相依网络和ER网络组成的相依网络的鲁棒性不为1,原因在于WS网络和ER网络的平均度
$ \lt k \gt $ 为2时,WS网络和ER网络可能为不完全连通图,存在若干个子图。综上所述,对相依边负载进行合理的分配,能减小相依边过载失效的故障率,提高网络的鲁棒性。2.2 网络组合形式对相依网络鲁棒性的影响
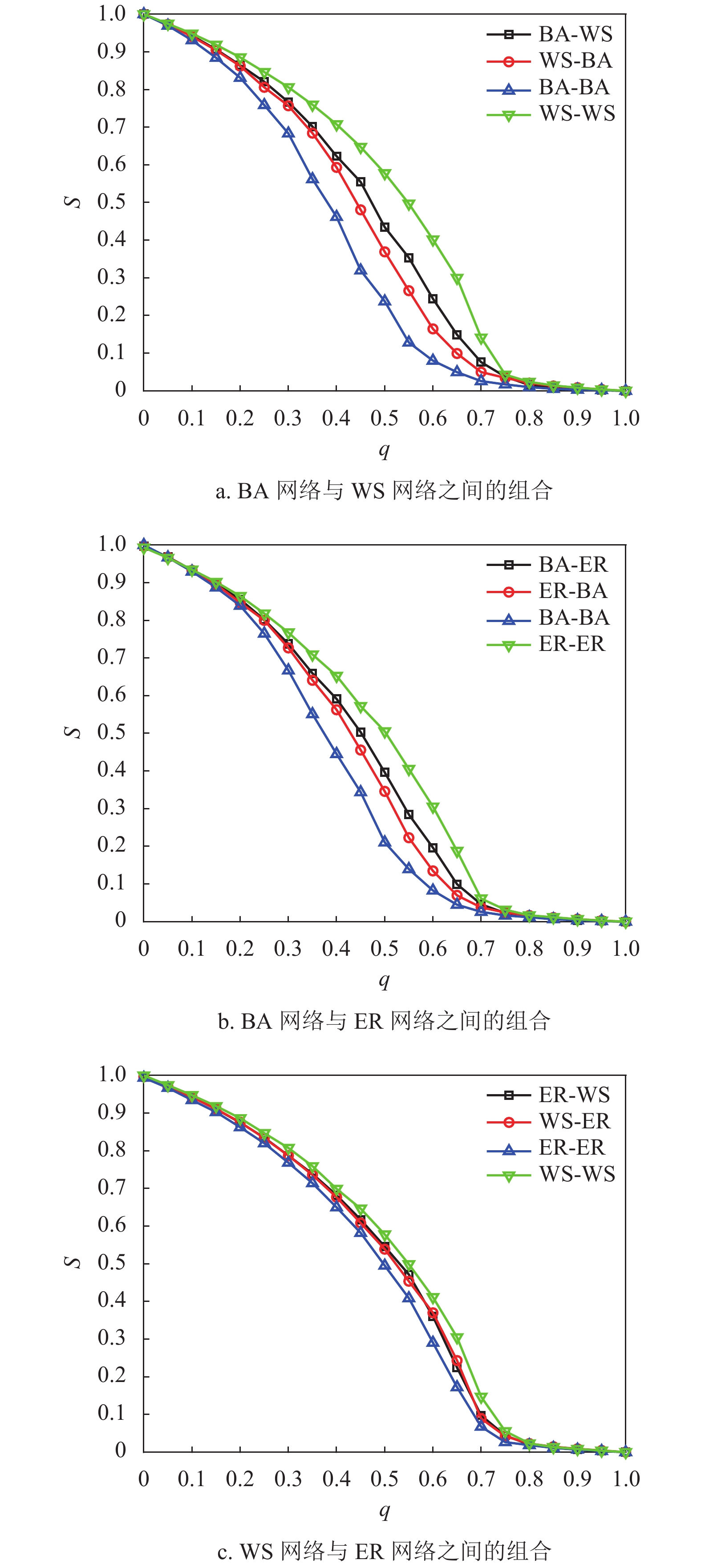
为考察不同网络组合对网络鲁棒性影响的差异性,设子网络的平均度
$ \lt k \gt $ =4,相依节点比例$ F $ =1,相依冗余度$ K $ =4,容忍系数$ \alpha $ =0.5,子网络之间随机耦合,并且相依边负载重分配采用负载分配策略,仿真分析相依网络的平均幸存节点比例和攻击节点比例的关系。仿真结果如图6所示。从图6中可以看出,在考虑相依边负载的相依网络模型中,不同的组合网络的平均幸存节点比例都随着攻击不断下降,当破坏比例达到0.8时,网络系统完全坍塌;在
$ 0.2 \leqslant {\text{q}} \leqslant 0.7 $ 时,网络的组合形式对系统抗毁性的区别最明显。WS-WS网络的下降速度在这些组合网络中最慢,BA-BA网络的鲁棒性最差,而ER-ER网络的抗毁性相对较好,混合网络则介于两者之间,并且混合相依网络相较与单一网络组成的依赖网络差异性更小。通过对比分析,考虑相依边负载的相依网络模型在不同的组合方式下的鲁棒性与文献[26]的研究结论类似,混合网络的鲁棒性往往介于两者之间,而本文考虑相依边负载的相依网络在WS-WS网络模式下抗毁性更加优异。2.3 子网络的平均度对网络鲁棒性的影响
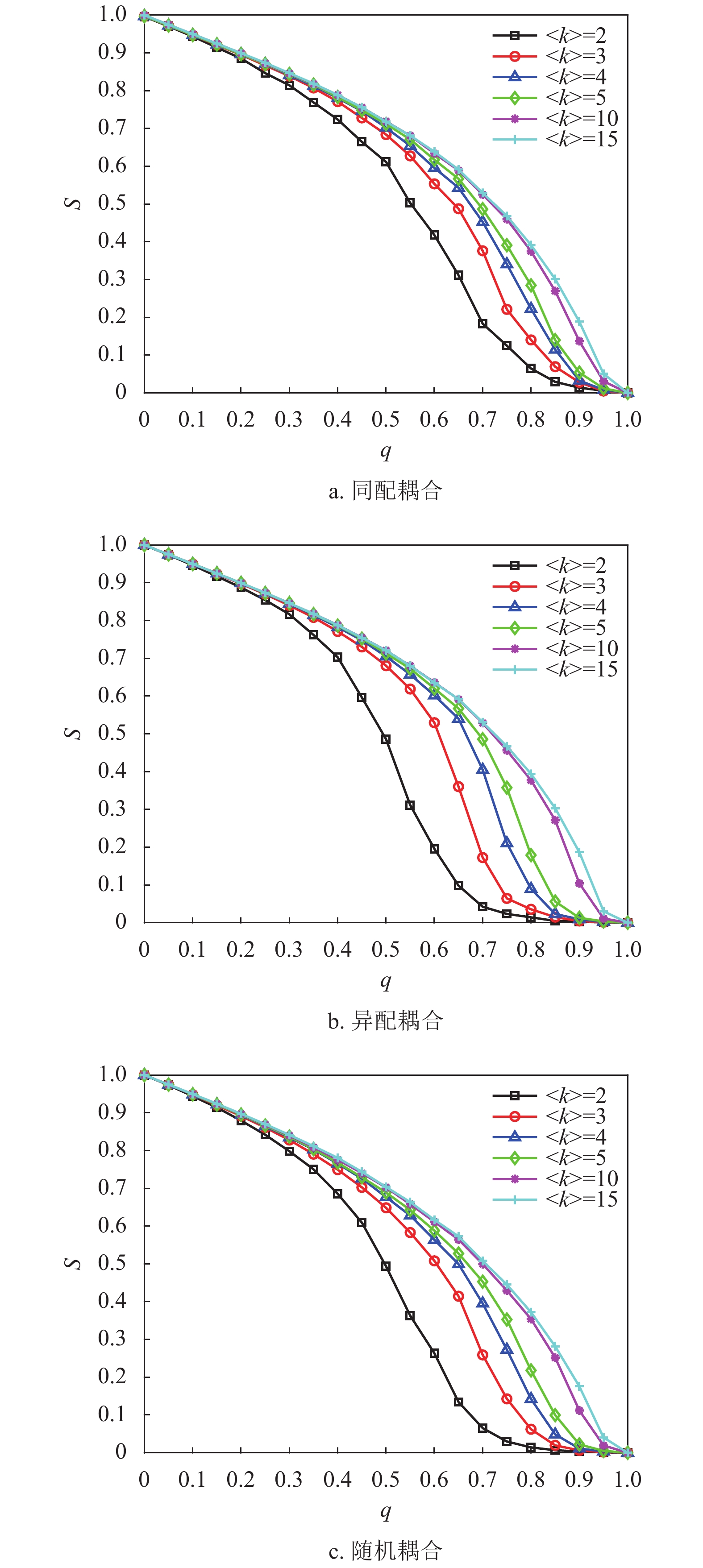
为分析子网络的平均度
$ \lt k \gt $ 对网络鲁棒性的影响,设容忍系数$ \alpha $ =0.8,两个子网络的模型为BA网络,相依节点比例$ F $ =1,相依冗余度$ K $ =4,并用同配、异配和随机耦合3种不同的耦合方式分别进行连接,采用的相依边负载重分配策略同上。仿真分析的结果如图7所示。由图7可知,随着子网络的平均度
$ \lt k \gt $ 增大,网络的鲁棒性也随之增加,同时当平均度$ \lt k \gt $ >5后,平均度对相依网络鲁棒性的强化有所减缓,而$ \lt k \gt \geqslant 10 $ 时,系统在同等破坏规模下幸存的有效节点比例差别并不明显,这说明子网络平均度对网络抗毁性优化有较强的局限性,虽然提高网络内节点的度值能有效地抵御非最大连通子图失效,但节点度值对网络整体失效的影响有一定限制。另外在$ 0.4 \leqslant q \leqslant 0.7 $ 时,相依系统中幸存节点减少较快,不同平均度对网络破坏程度的区别开始显现;当$ q \geqslant 0.7 $ 时系统的坍塌速率明显增加。且无论哪种耦合方式,整体下降趋势相同,而同配耦合下相依网络的鲁棒性最好。故此,提高子网络的平均度能在一定程度上改善网络系统的抗毁性。2.4 网络间的相依程度对相依系统鲁棒性的影响
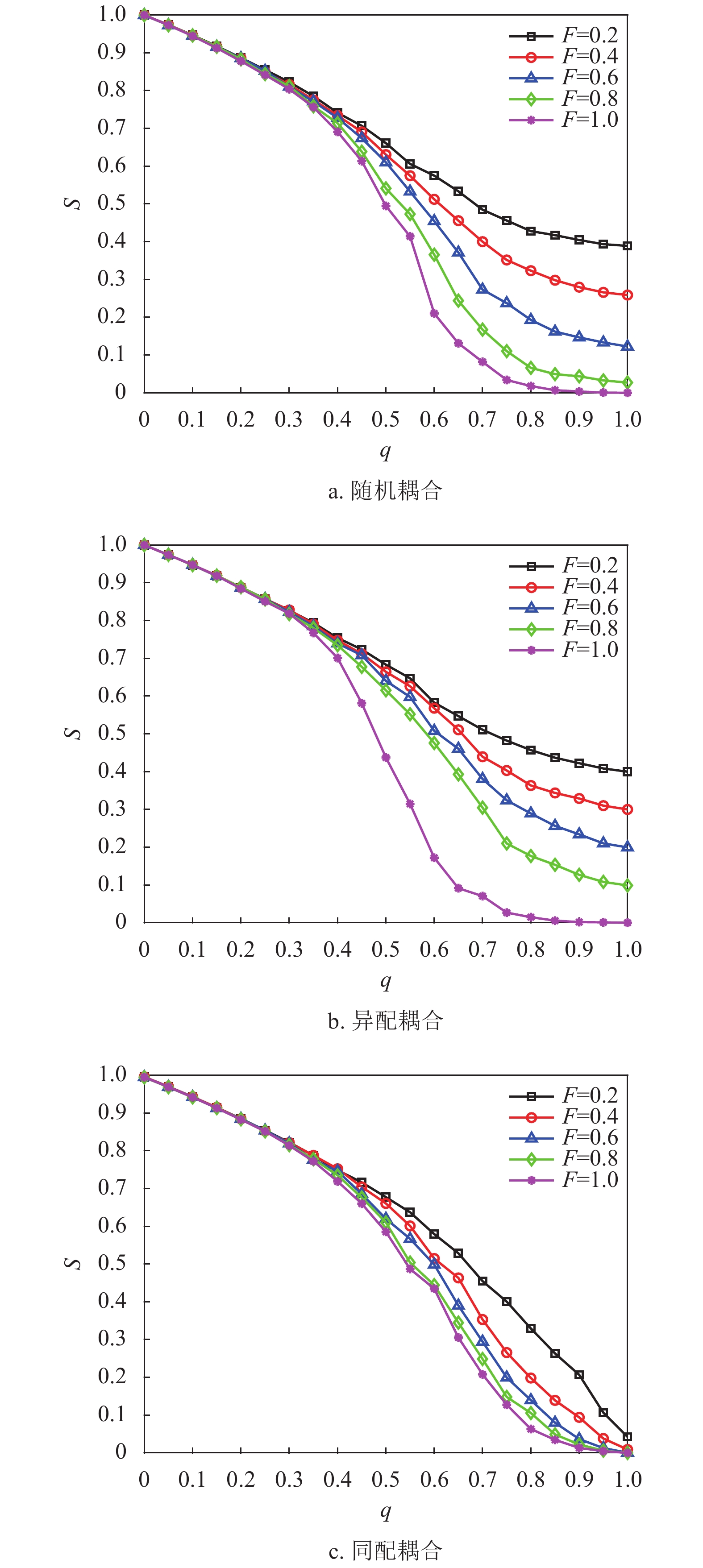
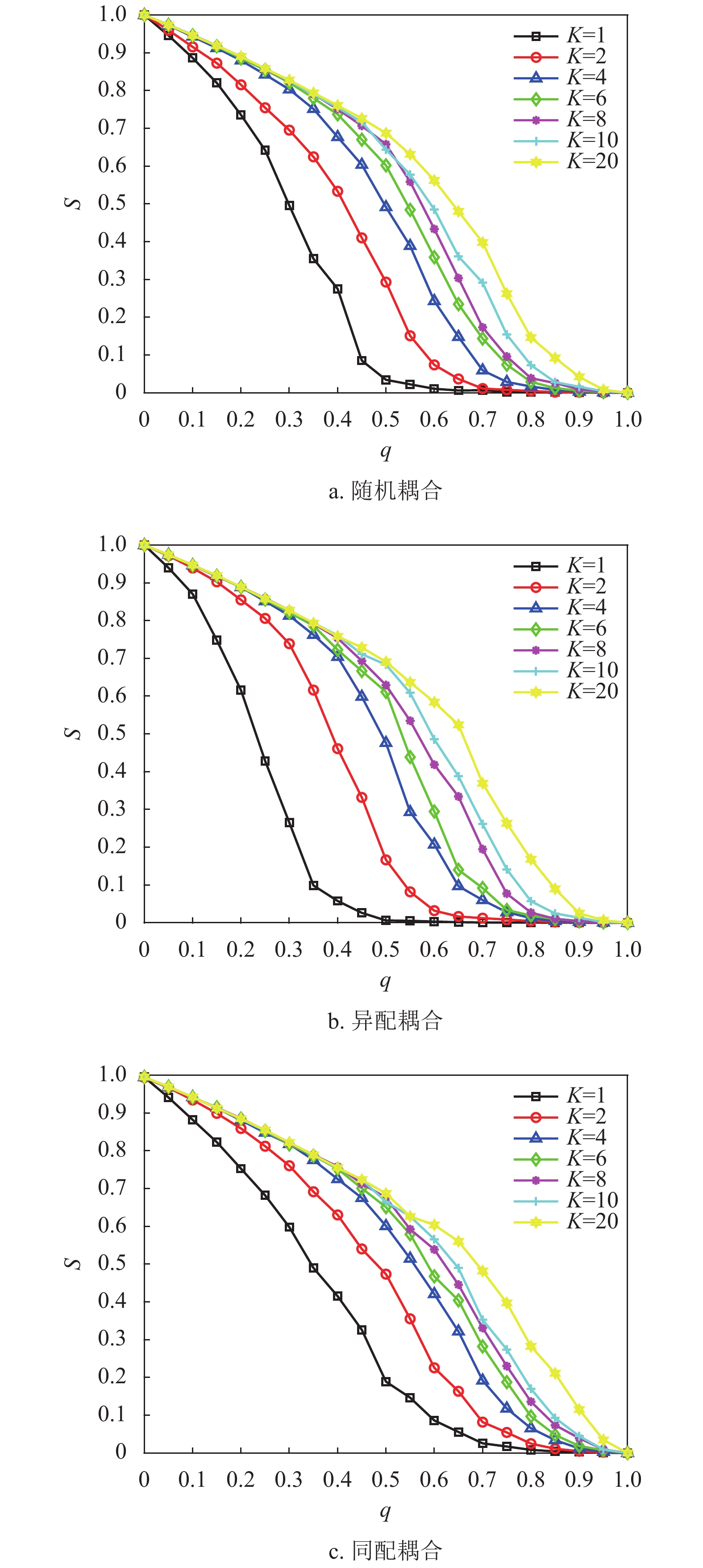
分析网络间的相依程度对网络系统的影响,两个子网络都为BA无标度网络,并以不同的耦合方式为研究对象,令子网络的平均度
$ \lt k \gt $ 为4,容忍系数和相依边负载重分配策略同上文一致。通过随机攻击子网络$ {G_A} $ 中的一定比例$ q $ 的节点,同时调节相依节点比例与相依冗余度的相对大小来进行仿真实验,仿真结果如图8和图9所示。从图8可知,在3种耦合模式下,网络系统的鲁棒性都随着攻击节点比例的增加而递减。且当相依冗余度
$ K $ 为4时,不同的相依节点比例对网络系统鲁棒性具有差异性。在攻击比例$ q $ =0.4时,不同的相依节点比例所导致的系统鲁棒性差异性开始显现,并随着攻击比例的增大,网络系统鲁棒性差异性越大。另外,相依节点比例越大,系统的鲁棒性越差,这与文献[19]中的结论相同,再次验证了相依节点比例对相依网络系统鲁棒性的影响。而且本文中相依节点比例的增加,增加了网络间信息沟通和传输的渠道,但这也利于相依边过载失效和相依失效的发生。从图9可知,在
$ F $ =1下,相依冗余度对相依网络系统的鲁棒性影响较大。随着相依冗余度的增加,相依网络系统的鲁棒性越强,即相依冗余度能有效地增强系统抵抗级联失效的抗毁性,原因在于每个节点的相依边数的增加有利于缓解相依失效和相依边过载失效,并且单个相依节点增加相依边也有助于分摊负载重分配时的额外负载,并减小相依失效的概率。此外随着相依冗余度$ K $ 的增加,$ K $ 对相依网络鲁棒性的影响在逐步减小。这与文献[19]中的结论相近,但本文考虑了相依边的负载重分配,所以系统鲁棒性的下降速率相较于文献[19]更迅速,下降比例也更大。综上所述,减少相依节点比例$ F $ ,提高相依冗余度$ K $ 能有效降低相依网络的崩溃比例。2.5 不同边攻击方式下相依网络的鲁棒性
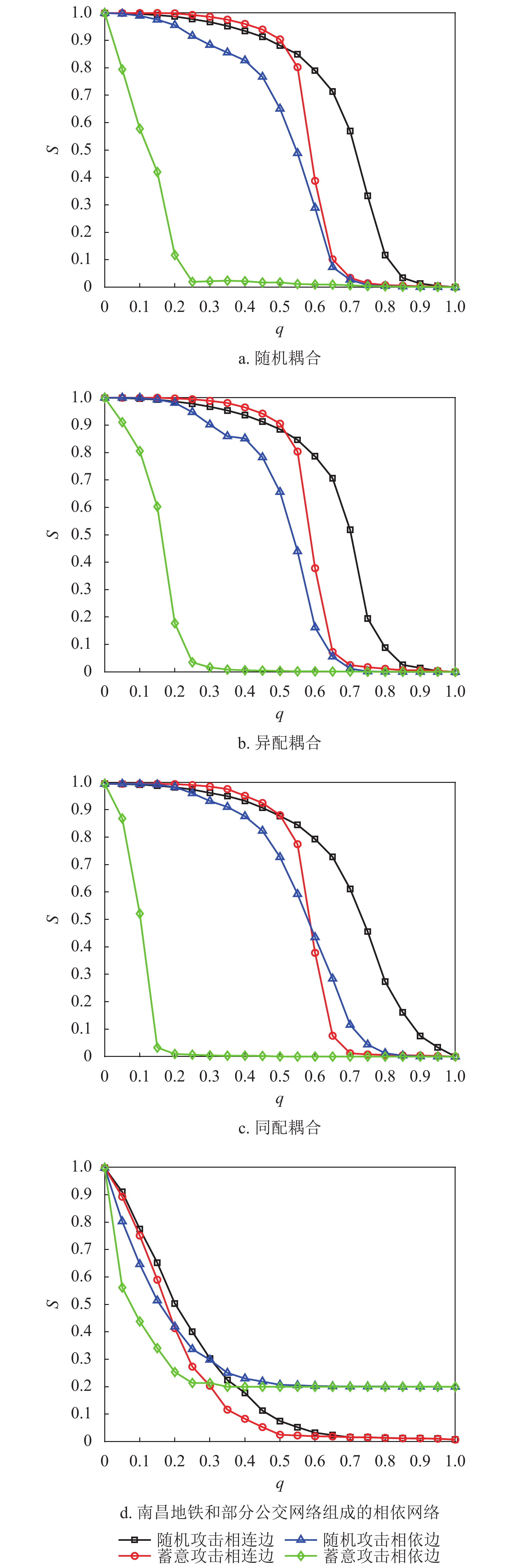
本节在初始失效时分别攻击一定比例的相连边和相依边,并通过系统处于稳定状态时鲁棒性指标的大小来判断相连边和相依边对相依网络的影响。在对系统进行蓄意攻击时,先对相连边进行加权处理,相连边的权重为连接节点度值的乘积,即
$ {w_{eij}} = {k_i} \times {k_j} $ 。初始状态时将相连边按权值降序排列,相依边按初始负载的大小降序排列,取前面一定比例的边进行攻击。若子网络中节点的相连边或相依边全都失效,则该节点失效。令系统的参数与负载重分配策略同上,子网络模型选择无标度网络和地铁公交网络,并通过上文中3种不同的耦合方式分别进行连接。在初始状态下,采用不用的攻击方式分别攻击相连边和相依边,分析系统网络的鲁棒性。仿真结果如图10所示。由图10可知,蓄意攻击比随机攻击对相依网络鲁棒性的影响更大,蓄意攻击相依边时系统网络的有效节点比例下降最快。因为攻击负载较大的相依边更容易导致相依边的过载失效和相依失效。且无论网络间的耦合采用何种方式,攻击相依边比攻击相连边对相依网络的失效风险更高。另外相比于其他耦合方式,相依网络在同配耦合下对于蓄意攻击产生的故障效果最明显,这是由于同配耦合时子网络间度值较大的节点相连接,使得失效的传播途径和故障范围更加广泛。此外,对真实地铁公交网络的仿真结果,也同样反映了相依边对网络系统的重要性,系统的整体下降趋势与无标度相依网络相似。相较于无标度网络组成的相依系统,地铁公交网络的失效速率和故障比例更大,原因在于地铁公交相依网络的子网络平均度和节点的相依冗余度较小,无法有效地抑制级联失效的传播。同时在地铁公交网络中子网络的节点总数不相等,相依节点的比例
$ {F_A} \ne {F_B} $ ,公交网络中存在较多没有相依边的节点,这就使得在攻击相依边时,会幸存大量没有相依边的节点,所以在攻击相依边的比例达到100%时,系统依然存在一些幸存节点。3. 结 束 语
在现实中不同网络之间信息或流量的传递与运输往往具有明显的负载效应,本文提出的考虑相依边负载的相依网络级联失效模型综合分析了此类现象。文中新定义了邻近相依边集,详细解释了相依边失效时负载重分配的原则。并通过人工网络和真实网络对这一现象进行说明,考虑相依边的负载会增加级联失效的复杂性,但同时这也更符合实际网络的故障状态,并探讨了耦合程度、子网络平均度和攻击方式等因素对考虑相依边负载的相依网络鲁棒性的影响。仿真结果表明了增强网络间的相互依赖比例会使得系统变得脆弱,但较大的相依冗余度能有效地遏制失效造成的破坏范围;提高子网络的平均度能显著地抵御网络内的非最大连通子图失效;相较于相连边,攻击相依边会加速整个网络系统的坍塌。这些研究对优化相依网络系统的鲁棒性提供了参考,也对现实中不同网络之间信息和流量的传递现象做出了一定的分析和解释。然而,这些研究都是在无向网络的基础上进行的,考虑相依边负载的级联失效模型对有向网络的影响有待进一步解决;此外,在对网络系统进行级联失效预防和恢复的过程中,文中所建立的失效模型如何增加恢复与预防的复杂性和困难程度是下一步研究的重点。
-
表 1 2021年6月南昌地铁与部分公交网络的相关参数
网络 节点数/个 相连边数/条 相依边数/条 平均度 $ \lt k \gt $ 地铁网络 70 71 393 1.014 3 市区公交网络 511 649 393 1.270 1 -
[1] 安天研究院. 广东省电力系统网络安全企业重点实验室. 委内瑞拉大规模停电事件的初步分析与思考启示[J]. 信息安全与通信保密, 2019, 5(1): 28-39. ANTIAN Research Institute. Guangdong province power systemnetwork security enterprise key laboratory. Preliminary analysis and reflections on large-scale power outage in Venezuela[J]. Information Security and Communication Privacy, 2019, 5(1): 28-39.
[2] ZHONG N S, ZENG G Q. Prevention and treatment of chronic respiratory diseases in China[J]. Chronic Diseases and Translational Medicine, 2019, 5(4): 209-213. DOI: 10.1016/j.cdtm.2019.12.006
[3] 苏枫. 堵船之殇: 聚焦苏伊士运河[J]. 小康, 2021(12): 48-50. SU F. Ship blocking: Focus on Suez canal[J]. Insight China, 2021(12): 48-50.
[4] BULDYREV S V, PARSHANI R, PAYL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028. DOI: 10.1038/nature08932
[5] MA F, LIU K F, YUEN K F, et al. Cascading failures and vulnerability evolution in bus-metro complex bilayer networks under rainstorm weather conditions[J]. International Journal of Environmental Research and Public Health, 2019, 16(3): 329. DOI: 10.3390/ijerph16030329
[6] HONG L, OUYANG M, XU M, et al. Time-varied accessibility and vulnerability analysis of integrated metro and high-speed rail systems[J]. Reliability Engineering and System Safety, 2020, 193: 1-10.
[7] 张艺伟, 刘文霞, 刘耕铭, 等. 考虑拓扑相关和双重耦合的电力信息物理系统建模与脆弱性分析[J]. 中国电机工程学报, 2021, 41(16): 5486-5500. DOI: 10.13334/J.0258-8013.PCSEE.210224 ZHANG Y W, LIU W X, LIU G M, et al. Modeling and vulnerability analysis of power information physical system considering topology correlation and double coupling[J]. Chinese Journal of Electrical Engineering, 2021, 41(16): 5486-5500. DOI: 10.13334/J.0258-8013.PCSEE.210224
[8] 孙晓璇, 吴晔, 冯鑫, 等. 高铁-普铁的实证双层网络结构与鲁棒性分析[J]. 电子科技大学学报, 2019, 48(2): 315-320. DOI: 10.3969/j.issn.1001-0548.2019.02.024 SUN X X, WU Y, FENG X, et al. Structure characteristics and robustness analysis of multi-layer network of high speed railway and ordinary railway[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(2): 315-320. DOI: 10.3969/j.issn.1001-0548.2019.02.024
[9] LIU Y Y, ZHAO C L, YI D Y, et al. Robustness of partially interdependent networks under combined attack[J]. Chaos (Woodbury N Y), 2019, 29(2): 021101. DOI: 10.1063/1.5085850
[10] WANG J D, LAO S Y, RUAN Y R, et al. Research on the robustness of interdependent networks under localized attack[J]. Applied Sciences, 2017, 7(6): 597. DOI: 10.3390/app7060597
[11] WANG X Y, ZHOU W J, LI R, et al. Improving robustness of interdependent networks by a new coupling strategy[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 492: 1075-1080. DOI: 10.1016/j.physa.2017.11.037
[12] ZANG W F, JI X S, LIU S X, et al. An interdependent network coupling strategy based on overlapping link structure against targeted attack[J]. International Journal of Modern Physics C, 2021, 32(8).
[13] GAO J X, BULDYREV S V, STANLEY H E, et al. Percolation of a general network of networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 88(6): 062816. DOI: 10.1103/PhysRevE.88.062816
[14] WANG N, JIN Z Y, ZHAO J. Cascading failures of overload behaviors on interdependent networks[J]. Physica A: Statistical Mechanics and its Applications, 2021, 574: 125989. DOI: 10.1016/j.physa.2021.125989
[15] LIU S, YIN C S, CHEN D J, et al. Modelling and impact analysis of interdependent characteristics on cascading overload failure of syncretic railway networks[J]. PloS One, 2020, 15(9): e0239096. DOI: 10.1371/journal.pone.0239096
[16] LIU J. Improving robustness of complex networks by a new capacity allocation strategy[J]. Chinese Physics B, 2021, 30(1): 016401. DOI: 10.1088/1674-1056/abb3f1
[17] SHEN Y, REN G, ZHANG N, et al. Effects of mutual traffic redistribution on robustness of interdependent networks to cascading failures under fluctuant load[J]. Physica A: Statistical Mechanics and its Applications, 2020, 560: DOI: 10.1016/j.physa.2020.125138.
[18] 陈世明, 邹小群, 吕辉, 等. 面向级联失效的相依网络鲁棒性研究[J]. 物理学报, 2014, 63(2): 432-441. DOI: 10.7498/aps.63.028902 CHEN S M, ZOU X Q, LU H, et al. Research on the robustness of dependent networks for cascade failure[J]. Acta Physics Sinica, 2014, 63(2): 432-441. DOI: 10.7498/aps.63.028902
[19] 陈世明, 吕辉, 徐青刚, 等. 基于度的正/负相关相依网络模型及其鲁棒性研究[J]. 物理学报, 2015, 64(4): 359-369. DOI: 10.7498/aps.64.048902 CHEN S M, LYU H, XU Q G, et al. Degree-based positive/negative correlation dependent network model and its robustness[J]. Acta Physics Sinica, 2015, 64(4): 359-369. DOI: 10.7498/aps.64.048902
[20] BARABASI A, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI: 10.1126/science.286.5439.509
[21] WATTS D J, STROGATZ S H. Collective dynamics of ’small-world’ networks[J]. Nature, 1998, 393(6684): 440-442. DOI: 10.1038/30918
[22] ERDS P, ALFRED R. On random graphs[J]. Publicationes Mathematicae, 1959, 6: 290-291.
[23] MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(2): 114-129.
[24] 赵娜, 柴焰明, 尹春林, 等. 基于最大连通子图相对效能的相依网络鲁棒性分析[J]. 电子科技大学学报, 2021, 50(4): 627-633. DOI: 10.12178/1001-0548.2020440 ZHAO N, CHAI Y M, YIN C L, et al. Robustness analysis of interdependent networks based on the largest-component relative efficiency[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(4): 627-633. DOI: 10.12178/1001-0548.2020440
[25] 刘凤增, 肖兵, 刘俊杰, 等. 级联失效下非对称依赖网络鲁棒性研究[J]. 国防科技大学学报, 2021, 43(1): 49-56. DOI: 10.11887/j.cn.202101007 LIU F Z, XIAO B, LIU J J, et al. Research on robustness of asymmetric dependent networks under cascading failure[J]. Journal of National University of Defense Technology, 2021, 43(1): 49-56. DOI: 10.11887/j.cn.202101007
[26] 王超, 郭基联, 沈安慰. 基于不对称依赖的相依网络级联故障分析[J]. 系统工程与电子技术, 2020, 42(5): 1093-1101. DOI: 10.3969/j.issn.1001-506X.2020.05.16 WANG C, GUO J L, SHEN A W. Cascade fault analysis of dependent networks based on asymmetric dependence[J]. Systems Engineering and Electronics, 2020, 42(5): 1093-1101. DOI: 10.3969/j.issn.1001-506X.2020.05.16
-
期刊类型引用(0)
其他类型引用(11)

 ISSN
ISSN 


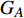
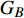
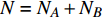
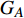
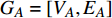
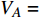
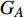
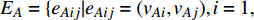
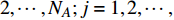
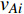
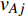
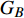
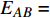
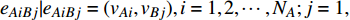
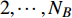
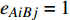
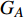
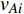
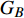
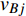
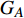
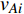
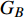
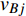
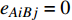
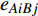
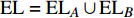
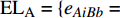
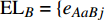
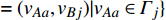
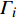
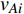
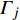
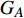
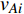
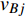
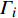
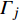
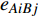
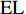
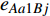
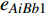
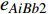
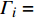
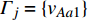
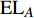
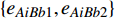
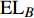
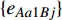
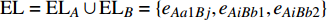
 下载:
下载: