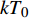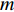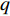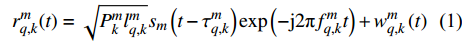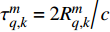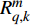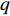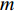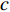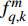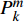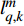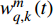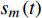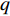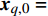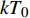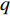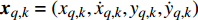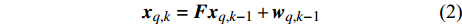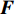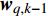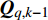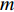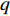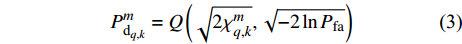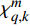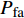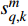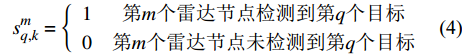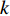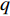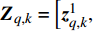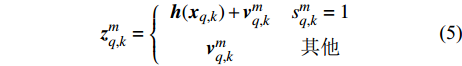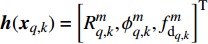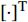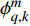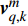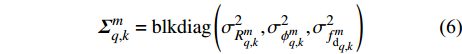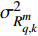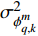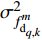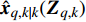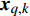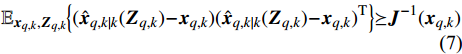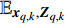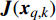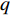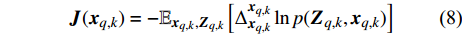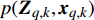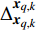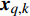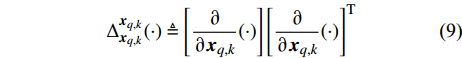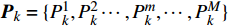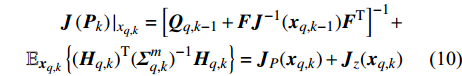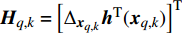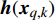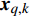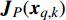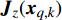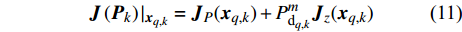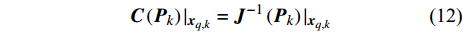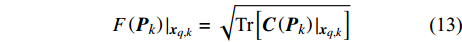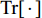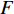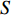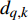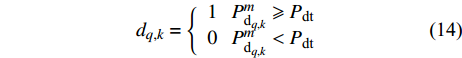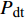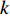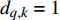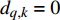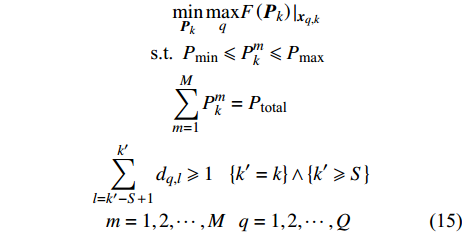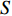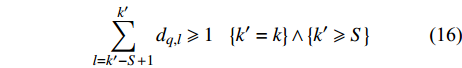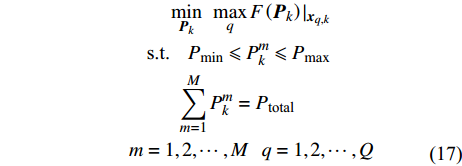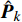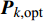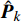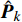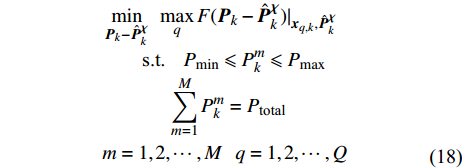A Radar Power Allocation Algorithm to Track Stably for a Long Track
-
摘要: 分布式组网雷达系统在处理跟踪任务时,低信噪比会导致目标检测概率小于1,进而可能导致目标航迹中断。为此,提出了一种长航迹稳定跟踪的分布式组网雷达功率分配算法,通过对雷达系统功率资源的优化配置,同时保证了航迹连续性与良好的系统跟踪性能。首先建立了分布式雷达回波信号及量测模型,然后推导了不确定性量测下的贝叶斯克拉美罗界(BCRLB),进而建立了功率分配问题数学模型。该优化问题中包含复杂非凸约束,为了对其进行高效求解,最后提出了一种基于凸优化的自约束功率分配(SCPA)算法。仿真结果表明,所提SCPA算法可以保证跟踪全阶段所有目标航迹不中断,并保持良好的跟踪性能。Abstract: In the tracking task of distributed radar networks, low signal-to-noise ratio will lead to detection probability of the target less than 1, which may lead to the interruption of target track. This paper proposes a power allocation algorithm for distributed radar networks to track stably for a long track. The track continuity and the tracking performance of the system are both guaranteed by optimizing the power allocation for radar nodes. First, signal and measurement models of distributed radar are established. Then, the Bayesian Cramér-Rao lower bound (BCRLB) under uncertainty measurements is derived, and a mathematical model of the power allocation problem is established. To efficiently solve the optimization problem which contains complex non-convex constraints, a self-constrained power allocation (SCPA) algorithm based on convex optimization is proposed. The simulation results show that the proposed SCPA algorithm can ensure that all target tracks are not interrupted in the whole tracking process, while keeping good tracking performance.
-
Keywords:
- distributed radar networks /
- power allocation /
- track stably /
- uncertain measurement
-
得益于空间分集增益,和传统体制雷达相比,分布式组网雷达系统在各方面均展现出显著的优点[1-3]。同时,空间广泛分布的多雷达节点为系统控制提供了更多自由度,因此,系统可通过对各种资源的优化配置获得更佳性能。当处理跟踪任务时,分布式组网雷达系统可通过对系统功率进行灵活分配,在系统总功率资源受限的条件下,实现跟踪性能的提高[4-6]。
雷达系统的跟踪过程是以对目标的量测为基础的,稳定的跟踪需要以良好的检测性能作为保障。在实际应用中,由于功率受限、信号的路径损耗等原因,雷达对目标的检测均为不完美检测,即存在一定的漏检概率。然而,已有的关于雷达功率分配的研究,大多数假设目标量测绝对可靠,这并不符合实际应用情况[4-6]。
现有的一些研究考虑了雷达系统功率分配中目标量测的不确定性,但这些研究致力于建立不确定性量测下的跟踪性能评价指标,没有考虑不确定性量测对航迹连续性的影响[7-8]。然而,在目标跟踪过程中,航迹连续性极为重要。连续的航迹会提供更多的目标信息,避免雷达反复进入扫描模式,造成资源浪费。连续的航迹也有利于对其进行融合处理,以提高跟踪性能。因此,本文研究针对多目标跟踪的分布式雷达功率分配方法,通过对功率资源的优化分配,保证航迹连续性与良好的系统跟踪性能。
1. 信号及量测模型
本章研究分布式雷达系统跟踪模型,分别建立了系统与信号模型、运动与量测模型,为优化问题的建模及求解建立了基础。
1.1 系统与信号模型
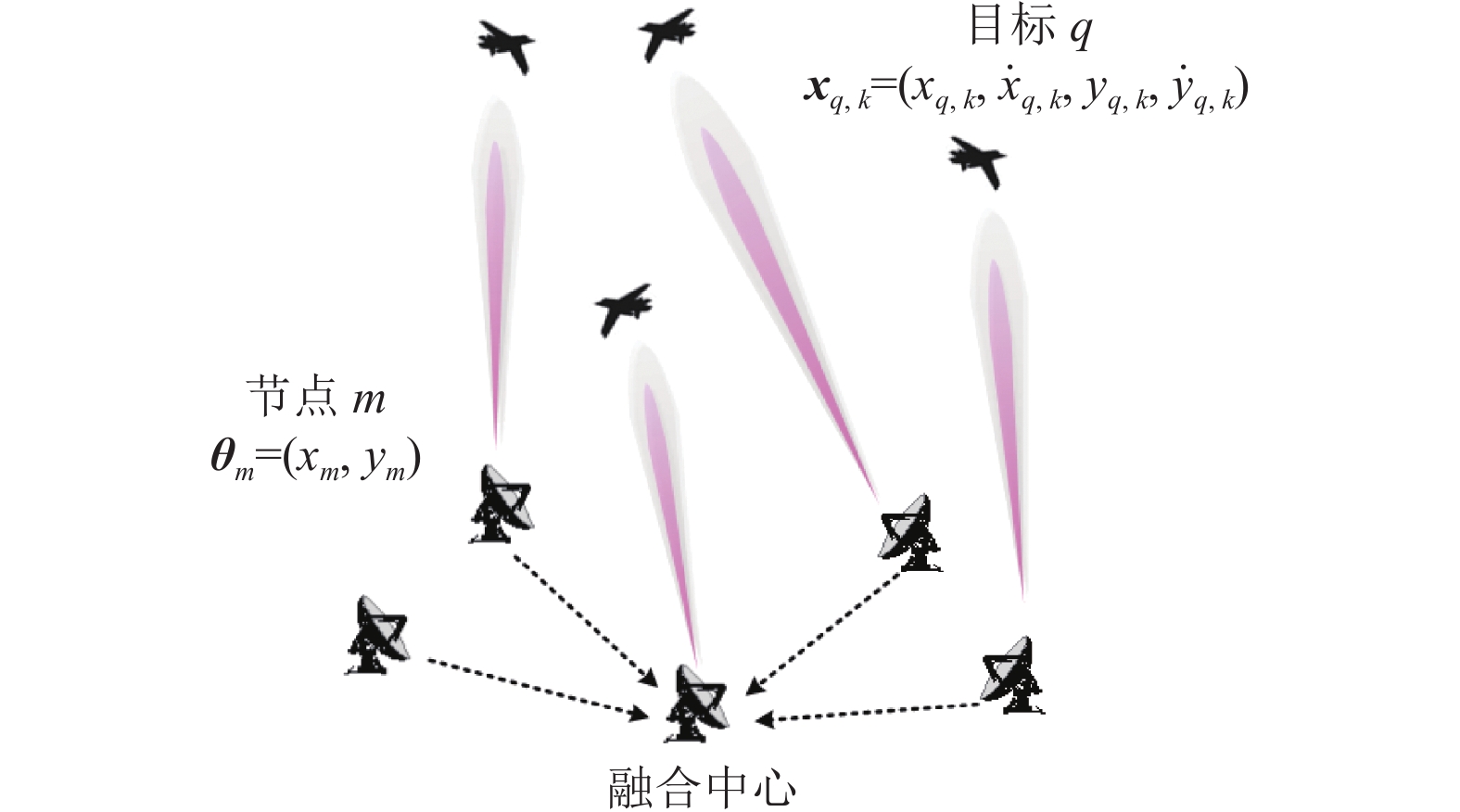
考虑一个由
$M$ 个雷达节点组成的分布式组网雷达系统,其中第$m$ 个节点位于${{\boldsymbol{\theta}} _m} = ({x_m},{y_m})$ ,如图1所示。各雷达节点工作在“自发自收”模式,并传输过门限的数据至融合中心进行联合处理。假设任务区域内有$Q$ 个分离的点目标,且$Q \leqslant M$ ,其中第$q$ 个目标的初始位置和初始速度分别为$( {{x_{q,0}},{y_{q,0}}} )$ 和$( {{{\dot x}_{q,0}},{{\dot y}_{q,0}}} )$ 。假设$ {T_0} $ 为观测时间间隔,则在$k{T_0}$ 时刻,第$q$ 个目标的位置及速度分别表示为$( {{x_{q,k}},{y_{q,k}}} )$ 和$( {{{\dot x}_{q,k}},{{\dot y}_{q,k}}} )$ 。假设在
$k{T_0}$ 时刻,第$m$ 个雷达节点所发射的信号被第$q$ 个目标反射,则接收信号可表示为:$$ r_{q,k}^m(t) = \sqrt {P_k^ml_{q,k}^m} {s_m}\left( {t - \tau _{q,k}^m} \right)\exp \left( { - {\rm{j}}2{\text π} f_{q,k}^mt} \right) + w_{q,k}^m\left( t \right) $$ (1) 式中,
$ \tau _{q,k}^m = {{2R_{q,k}^m} \mathord{\left/ {\vphantom {{2R_{q,k}^m} c}} \right. } c} $ 表示传输时延;$ R_{q,k}^m $ 为第$q$ 个目标与第$m$ 个雷达节点之间的距离;$ c $ 为光速;$f_{q,k}^m$ 表示多普勒频移;$ P_k^m $ 为发射功率;$ l_{q,k}^m $ 表示路径损耗;$ w_{q,k}^m\left( t \right) $ 为零均值复高斯白噪声;$ {s_m}\left( t \right) $ 为发射信号的归一化复包络。1.2 运动与量测模型
假设第
$q$ 个目标的初始状态可表示为${{\boldsymbol{x}}_{q,0}} = ( {{x_{q,0}},{{\dot x}_{q,0}},{y_{q,0}},{{\dot y}_{q,0}}} )$ ,在$k{T_0}$ 时刻,第$q$ 个目标的状态可表示为${{\boldsymbol{x}}_{q,k}} = ( {{x_{q,k}},{{\dot x}_{q,k}},{y_{q,k}},{{\dot y}_{q,k}}} )$ 。不失一般性,假设目标为匀速直线运动,则运动模型为:$$ {{\boldsymbol{x}}_{q,k}} = {\boldsymbol{F}}{{\boldsymbol{x}}_{q,k - 1}} + {{\boldsymbol{w}}_{q,k - 1}} $$ (2) 式中,
$ {\boldsymbol{F}} $ 为状态转移矩阵;$ {{\boldsymbol{w}}_{q,k - 1}} $ 表示协方差为$ {{\boldsymbol{Q}}_{q,k - 1}} $ 的零均值高斯过程噪声。通过信号处理,可以从接收信号中提取多种目标信息,本文主要关注时延、方位及多普勒信息。第
$m$ 个雷达节点对第$q$ 个目标的检测概率可以表示为[9]:$$ P_{{\text{d}}_{q,k}}^m = Q\left( {\sqrt {2\chi _{q,k}^m} ,\sqrt { - 2\ln {P_{{\rm{fa}}}}} } \right) $$ (3) 式中,
${{Q}}( \cdot )$ 为Marcum-Q函数;$ \chi _{q,k}^m $ 为接收信号的信噪比;$ {P_{{\rm{fa}}}} $ 表示虚警概率。定义
$ s_{q,k}^m $ 为检测变量:$$ {s}_{q,k}^{m}=\left\{\begin{array}{cc}1 & 第m个雷达节点检测到第q个目标\\ 0 & 第m个雷达节点未检测到第q个目标\end{array}\right. $$ (4) 则在第
$k$ 帧,第$q$ 个目标的量测可表示为${{\boldsymbol{Z}}_{q,k}} = \left[ {{ {\textit{z}}}}_{q,k}^1, \right. \left. {{ {\textit{z}}}}_{q,k}^2, \cdots ,{{ {\textit{z}}}}_{q,k}^m, \cdots ,{{ {\textit{z}}}}_{q,k}^M \right]$ ,其中:$$ {{ {\textit{z}}}}_{q,k}^{m}=\left\{\begin{array}{cc}{\boldsymbol{h}}({{\boldsymbol{x}}}_{q,k})+{{\boldsymbol{v}}}_{q,k}^{m}& {s}_{q,k}^{m}=1\\ {{\boldsymbol{v}}}_{q,k}^{m}& 其他\end{array} \right.$$ (5) 式中,
${\boldsymbol{h}}( {{{\boldsymbol{x}}_{q,k}}} ) = {\left[ {R_{q,k}^m,\phi _{q,k}^m,f_{{\text{d}}_{q,k}}^m} \right]^{\rm{T}}}$ 为量测函数;$ {[ \cdot ]^{\rm{T}}} $ 为转置符号;$ \phi _{q,k}^m $ 表示方位角;$ {\boldsymbol{v}}_{q,k}^m $ 为零均值高斯随机噪声,其方差为:$$ \displaystyle{{{\boldsymbol{\varSigma}}}_{q,k}^m }= {{\rm{blkdiag}}} \left( {\sigma _{R_{q,k}^m}^2,\sigma _{\phi _{q,k}^m}^2,\sigma _{f_{{\text{d}}_{q,k}}^m}^2} \right) $$ (6) 式中,
$ \sigma _{R_{q,k}^m}^2 $ 、$ \sigma _{\phi _{q,k}^m}^2 $ 和$ \sigma _{f_{{\text{d}}_{q,k}}^m}^2 $ 分别为距离、角度、多普勒估计均方根误差的克拉美罗下界。由于量测模型非线性,采取扩展卡尔曼滤波对目标状态进行估计。
2. 基于凸优化的功率分配方法
本章研究分布式组网雷达系统功率分配方法。首先给出了量测不确定情况下的贝叶斯克拉美罗界(Bayesian Cramér-Rao lower bound, BCRLB),然后建立了功率分配数学模型,最后提出了一种基于凸优化的自约束功率分配算法,对功率分配问题进行求解。
2.1 贝叶斯克拉美罗界
贝叶斯克拉美罗界BCRLB提供了目标状态的估计误差的下界,因此被广泛应用于评估雷达系统的跟踪性能。假设
${\hat {\boldsymbol{x}}_{q,k\mid k}}( {{{\boldsymbol{Z}}_{q,k}}})$ 为${{\boldsymbol{x}}_{q,k}}$ 的估计,根据贝叶斯−克拉美罗不等式可得[10-11]:$$ {\mathbb{E}_{{{\boldsymbol{x}}_{q,k}},{{\boldsymbol{Z}}_{q,k}}}} \left\{ {( {{{\hat {\boldsymbol{x}}}_{q,k\mid k}}( {{{\boldsymbol{Z}}_{q,k}}} ) - {{\boldsymbol{x}}_{q,k}}} ){{( {{{\hat {\boldsymbol{x}}}_{q,k\mid k}}( {{{\boldsymbol{Z}}_{q,k}}} ) - {{\boldsymbol{x}}_{q,k}}} )}^{\rm{T}}}} \right\} \succeq {{\boldsymbol{J}}^{ - 1}}( {{{\boldsymbol{x}}_{q,k}}} ) $$ (7) 式中,
${\mathbb{E}_{{{\boldsymbol{x}}_{q,k}},{{\boldsymbol{Z}}_{q,k}}}}$ 表示关于量测与目标状态的数学期望;${\boldsymbol{J}}( {{{\boldsymbol{x}}_{q,k}}} )$ 表示第$q$ 个目标的贝叶斯信息矩阵:$$ {\boldsymbol{J}}( {{{\boldsymbol{x}}_{q,k}}}) = - {\mathbb{E}_{{{\boldsymbol{x}}_{q,k}},{{\boldsymbol{Z}}_{q,k}}}}\left[ {\Delta _{{{\boldsymbol{x}}_{q,k}}}^{{{\boldsymbol{x}}_{q,k}}}\ln p( {{{\boldsymbol{Z}}_{q,k}},{{\boldsymbol{x}}_{q,k}}} )} \right] $$ (8) 式中,
$ p( {{{\boldsymbol{Z}}_{q,k}},{{\boldsymbol{x}}_{q,k}}} ) $ 表示量测和目标状态的联合概率密度函数;$\Delta _{{{\boldsymbol{x}}_{q,k}}}^{{{\boldsymbol{x}}_{q,k}}}$ 为关于$ {{\boldsymbol{x}}_{q,k}} $ 的二阶偏导算子:$$ \Delta _{{{\boldsymbol{x}}_{q,k}}}^{{{\boldsymbol{x}}_{q,k}}}( \cdot ) \triangleq \left[ {\frac{\partial }{{\partial {{\boldsymbol{x}}_{q,k}}}}( \cdot )} \right]{\left[ {\frac{\partial }{{\partial {{\boldsymbol{x}}_{q,k}}}}( \cdot )} \right]^{\rm{T}}} $$ (9) 定义
${{\boldsymbol{P}}_k} = \{ P_k^1,P_k^2\cdots,P_k^m,\cdots,P_k^M\}$ 为所有雷达节点的发射功率集合。如果不考虑检测的不确定性,则贝叶斯信息矩阵可以简单表示为[10-11]:$$ \begin{split} {\boldsymbol{J}}\left( {{{\boldsymbol{P}}_k}} \right){|_{{x_{q,k}}}} = {\left[ {{{\boldsymbol{Q}}_{q,k - 1}} + {\boldsymbol{F}}{{\boldsymbol{J}}^{ - 1}}( {{{\boldsymbol{x}}_{q,k - 1}}} ){{\boldsymbol{F}}^{\rm{T}}}} \right]^{ - 1}} + \\ {\mathbb{E}_{{{\boldsymbol{x}}_{q,k}}}}\left\{ {{{({{\boldsymbol{H}}_{q,k}})}^{\rm{T}}}{{({\boldsymbol{\varSigma}} _{q,k}^m)}^{ - 1}}{{\boldsymbol{H}}_{q,k}}} \right\} = {{\boldsymbol{J}}_P}( {{{\boldsymbol{x}}_{q,k}}} ) + {{\boldsymbol{J}}_z}( {{{\boldsymbol{x}}_{q,k}}} ) \end{split} $$ (10) 式中,
${{\boldsymbol{H}}_{q,k}} = {\left[ {{\Delta _{{{\boldsymbol{x}}_{q,k}}}}{{\boldsymbol{h}}^{\rm{T}}}( {{{\boldsymbol{x}}_{q,k}}} )} \right]^{\rm{T}}}$ 表示${\boldsymbol{h}}( {{{\boldsymbol{x}}_{q,k}}} )$ 关于$ {{\boldsymbol{x}}_{q,k}} $ 的雅克比函数;${{\boldsymbol{J}}_P}( {{{\boldsymbol{x}}_{q,k}}} )$ 和${{\boldsymbol{J}}_z}( {{{\boldsymbol{x}}_{q,k}}} )$ 分别为先验信息和数据的费舍尔信息矩阵。当考虑到检测的不确定性后,贝叶斯信息矩阵被修正为以下形式[10]:
$$ {\boldsymbol{J}}\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}} = {{\boldsymbol{J}}_P}( {{{\boldsymbol{x}}_{q,k}}} ) + P_{{\text{d}}_{q,k}}^m {{\boldsymbol{J}}_z}( {{{\boldsymbol{x}}_{q,k}}} ) $$ (11) 然后,贝叶斯克拉美罗界被定义为贝叶斯信息矩阵的逆:
$$ {\boldsymbol{C}}\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}} = {{\boldsymbol{J}}^{ - 1}}\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}} $$ (12) 本文以BCRLB的迹作为目标跟踪精度评价指标,即:
$$ F\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}} = \sqrt {{\text{Tr}}\left[ {{\boldsymbol{C}}\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}}} \right]} $$ (13) 式中,
$ {\text{Tr[}} \cdot {\text{]}} $ 表示取迹操作。一个更大的$ F $ 值等效于更差的跟踪精度,反之亦然。同时注意到,此指标针对的是每一帧的系统跟踪性能,但无法直接反映跟踪航迹的质量,如航迹连续性。2.2 功率分配数学模型
本文考虑优化最差性能的目标的跟踪精度,从而使所有目标均可被良好跟踪。同时,为了保证航迹的连续性,需要保证目标不能在连续
$S$ 帧内未被有效检测[12]。首先,定义有效检测指示函数$ {d_{q,k}} $ ,用于对检测不确定性进行刻画,具体表示为:$$ {d_{q,k}} = \left\{ {\begin{array}{*{20}{l}} {1{\text{ }}\;\;P_{{\text{d}}_{q,k}}^m \geqslant {P_{{\text{dt}}}}} \\ {0{\text{ }}\;\;P_{{\text{d}}_{q,k}}^m < {P_{{\text{dt}}}}} \end{array}} \right. $$ (14) 式中,
$ {P_{{\text{dt}}}} $ 为预设的检测概率阈值。式(14)表示,在第$k$ 帧,若雷达节点对目标的检测概率不小于预设检测概率阈值,则认为系统对目标有效检测,此时$ {d_{q,k}} = 1 $ ;否则,认为系统未对目标有效检测,此时$ {d_{q,k}} = 0 $ 。基于以上定义与分析,功率分配问题可表示为:
$$ \begin{split}& \qquad\qquad \underset{{{\boldsymbol{P}}}_{k}}{\mathrm{min}}\,\underset{q}{\mathrm{max}}F\left({{\boldsymbol{P}}}_{k}\right){|}_{{{\boldsymbol{x}}}_{q,k}}\\& \qquad\;\;\;\; \text{s}\text{.t}\text{.}\;\;{P}_{\mathrm{min}}\leqslant {P}_{k}^{m}\leqslant {P}_{\mathrm{max}}\\& \qquad\qquad{\displaystyle \sum _{m=1}^{M}{P}_{k}^{m}={P}_{\text{total}}}\\&{\displaystyle \sum _{l=k{'}-S+1}^{k{'}}{d}_{q,l}\geqslant 1}\;\;\;\left\{k{'}=k\right\}\wedge \left\{k{'}\geqslant S\right\}\\& \;\;\;m=1,2,\cdots,M\;\;\;q=1,2,\cdots,Q \end{split} $$ (15) 式中,前两条约束与雷达功率资源相关,分别表示:1)雷达辐射功率有最小和最大功率的约束限制;2)雷达系统功率总和为一定值。
最后一条约束为航迹连续性约束,以保证跟踪航迹的连续性,其表示不存在在连续的
$ S $ 帧内目标均未被有效检测的情况,由此保证雷达系统跟踪航迹不中断。2.3 自约束功率分配算法
由于优化问题(15)中,最后一条约束为复杂非凸约束,因此此类问题无法使用标准的凸优化算法,如梯度投影等求解[13]。而各种启发式算法(如遗传算法、模拟退火算法等)通常计算量较大,无法满足实时性优化的要求[14]。因此,提出一个基于凸优化的自约束功率分配(self-constrained power allocation, SCPA)算法,对功率分配问题(15)进行求解。
注意到,若将式(15)中的约束进行拆分,将其中有关航迹连续性的约束,即:
$$ {\displaystyle \sum _{l=k{'}-S+1}^{k{'}}{d}_{q,l}\geqslant 1}\;\;\;\left\{k{'}=k\right\}\wedge \left\{k{'}\geqslant S\right\} $$ (16) 暂时忽略,则功率分配问题变为一个标准凸优化问题:
$$\begin{split}&\qquad\qquad \mathop {\min }\limits_{{{\boldsymbol{P}}_k}} \;\;\mathop {\max }\limits_q F\left( {{{\boldsymbol{P}}_k}} \right){|_{{{\boldsymbol{x}}_{q,k}}}} \\&\qquad\;\;\;\; {\text{s}}{\text{.t}}{\text{.}}\;\;\;\;{P_{\min }} \leqslant P_k^m \leqslant {P_{\max }} \\&\qquad\qquad \;\;\sum\limits_{m = 1}^M {P_k^m = {P_{{\text{total}}}}} \\&\qquad m = 1,2,\cdots,M\;\;\;q = 1,2,\cdots,Q \\ \end{split}$$ (17) 优化问题(17)可以通过梯度投影等标准凸优化算法进行求解,将式(17)所求的优化解记为
$ {\hat {\boldsymbol P}_k} $ 。在
$ S $ 帧之前,跟踪航迹不受航迹连续性约束式(16)的限制,此时最终的优化解$ {{\boldsymbol P}_{k,{\text{opt}}}} $ 即为$ {\hat {\boldsymbol P}_k} $ 。然而在$S$ 帧之后,由于受到航迹连续性约束式(16)的限制,优化解$ {\hat {\boldsymbol P}_k} $ 不一定是原优化问题式(15)的可行解。因此,从第$S$ 帧开始,需要考虑航迹连续性约束对功率分配的影响,并基于优化问题式(17)的解$ {\hat {\boldsymbol P}_k} $ 进行进一步处理,从而得到最终的功率分配结果$ {{\boldsymbol P}_{k,{\text{opt}}}} $ 。具体方法如下。1) 基于解
$ {\hat {\boldsymbol P}_k} $ 表示的功率分配结果,判断各雷达节点是否满足航迹连续性约束式(16)。若约束满足,则输出$ {{\boldsymbol P}_{k,{\text{opt}}}} = {\hat {\boldsymbol P}_k} $ 。若约束不满足,则将所有不满足式(16)的节点标号提取并记为${\boldsymbol{\chi}} = \left\{ {{m_i}} \right\}_{i = 1}^I$ ,其中$I$ 表示所有不满足航迹连续性约束的雷达节点个数。2) 针对第
$ {m_i} $ (${m_i} \in {\boldsymbol{\chi}}$ )个雷达节点,将其发射功率改变为$ \hat P_k^{{m_i}} = P_{k,\min }^{{m_i}} $ ,其中$ P_{k,\min }^{{m_i}} $ 表示令目标检测概率刚好等于检测概率阈值的发射功率。3) 重复步骤2) 共
$I - 1$ 次,令所有不满足航迹连续性约束式(16)的节点,通过改变发射功率,满足航迹连续性约束。4) 固定所有
$\hat P_k^{{m_i}}({m_i} \in {\boldsymbol{\chi}} )$ ,即$\hat {\boldsymbol{P}}_k^{\boldsymbol{\chi}}$ ,并代入到优化问题式(17)中,对其余$M - I$ 个节点功率二次优化,即:$$ \begin{split}& \mathop {\min }\limits_{{{\boldsymbol{P}}_k} - \hat {\boldsymbol{P}}_k^{\boldsymbol{\chi}} } \;\;\mathop {\max }\limits_q F( {{{\boldsymbol{P}}_k} - \hat {\boldsymbol{P}}_k^{\boldsymbol{\chi}} } ){|_{{{\boldsymbol{x}}_{q,k}},\hat {\boldsymbol{P}}_k^{\boldsymbol{\chi}} }} \\[-2pt]&\qquad {\text{s}}{\text{.t}}{\text{.}}\;\;\;\;{P_{\min }} \leqslant P_k^m \leqslant {P_{\max }} \\[-2pt]&\qquad \;\;\;\;\;\;\sum\limits_{m = 1}^M {P_k^m = {P_{{\text{total}}}}} \\& m = 1,2,\cdots,M\;\;\;q = 1,2,\cdots,Q\;\;\; \\ \end{split}$$ (18) 5) 结合步骤2) , 3) , 4) 的优化结果,得到更新后的功率分配结果
${\hat {\boldsymbol{P}}_k}$ ,重复步骤1)。3. 仿真结果及分析
为了验证所提功率分配算法的有效性,考虑一个多目标跟踪的仿真场景。雷达节点数为4,节点位置分别为[−60,0] km、[−20,0] km、[20,0] km和[60,0] km,监视周期为40帧,观测时间间隔为2 s。雷达系统主要参数为:雷达节点有效时宽0.1 ms,有效带宽1 MHz,系统总功率100 dBw。功率约束分别为
$ {P_{\min }} = 0.1{P_{{\text{total}}}} $ 和$ {P_{\max }} = 0.9{P_{{\text{total}}}} $ ,检测概率阈值为$ {P_{{\text{dt}}}} = 0.7 $ ,航迹连续性约束中取$ S = 3 $ 。优化问题式(17)和式(18)均利用凸优化工具包CVX进行求解,所有仿真均进行300次蒙特卡洛实验。为了验证所提SCPA算法的有效性,以另一种常见固定功率分配(fixed power allocation, FPA)算法作为对比,即系统总功率平均分给各个雷达节点。
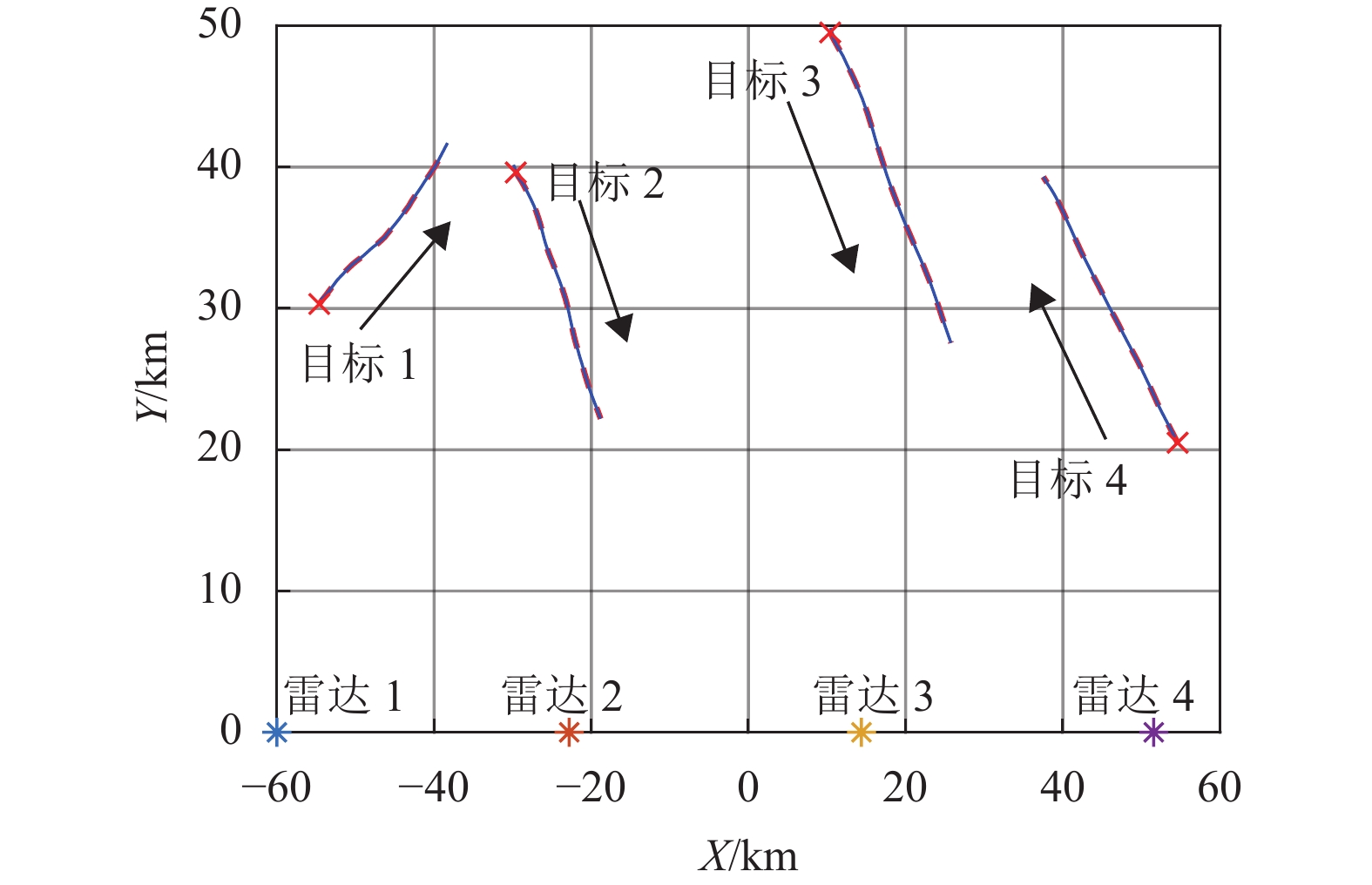
假设目标数为4,编号1~4的雷达节点分别对编号1~4的目标进行跟踪,目标的运动轨迹如图2所示。
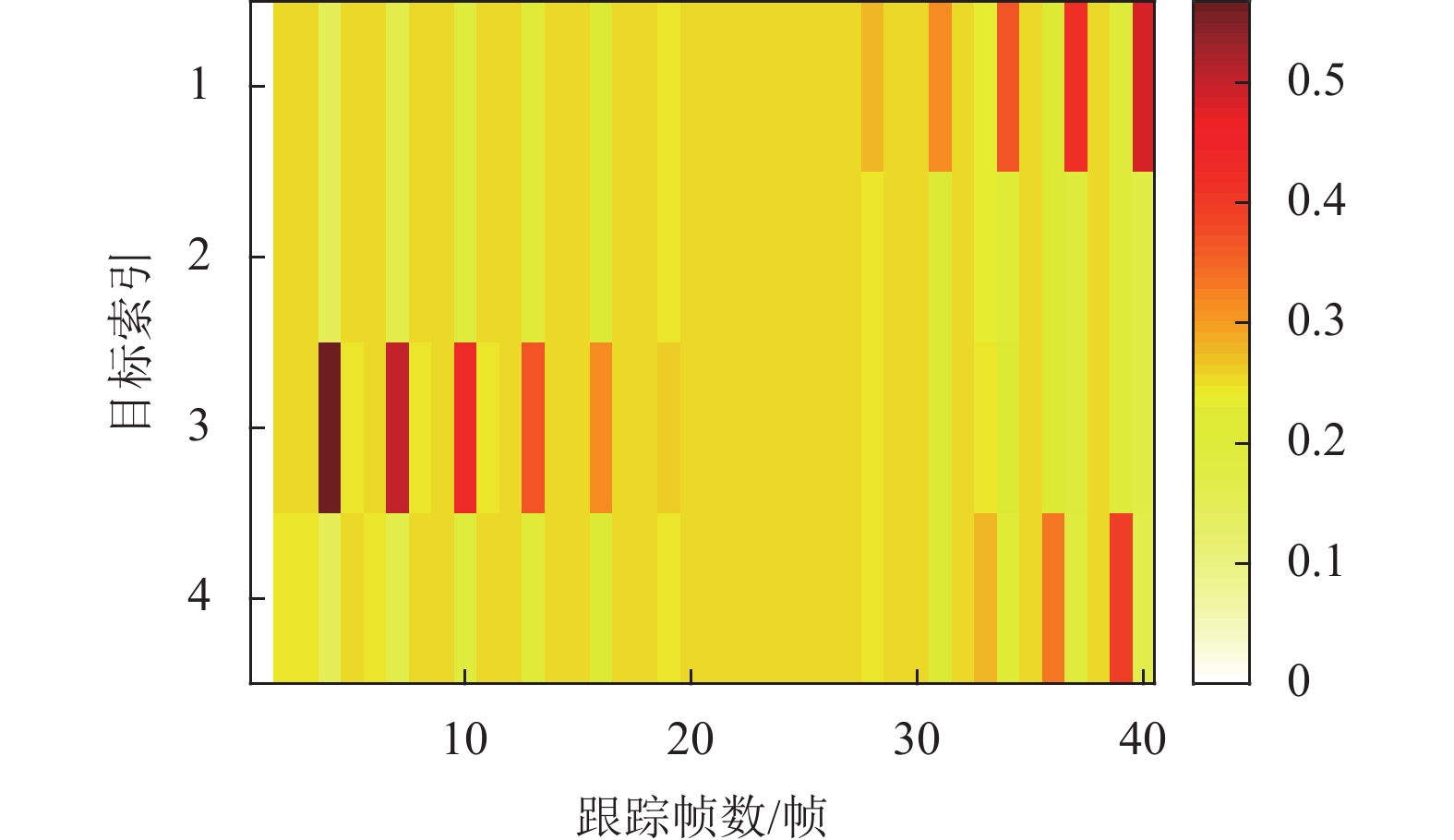
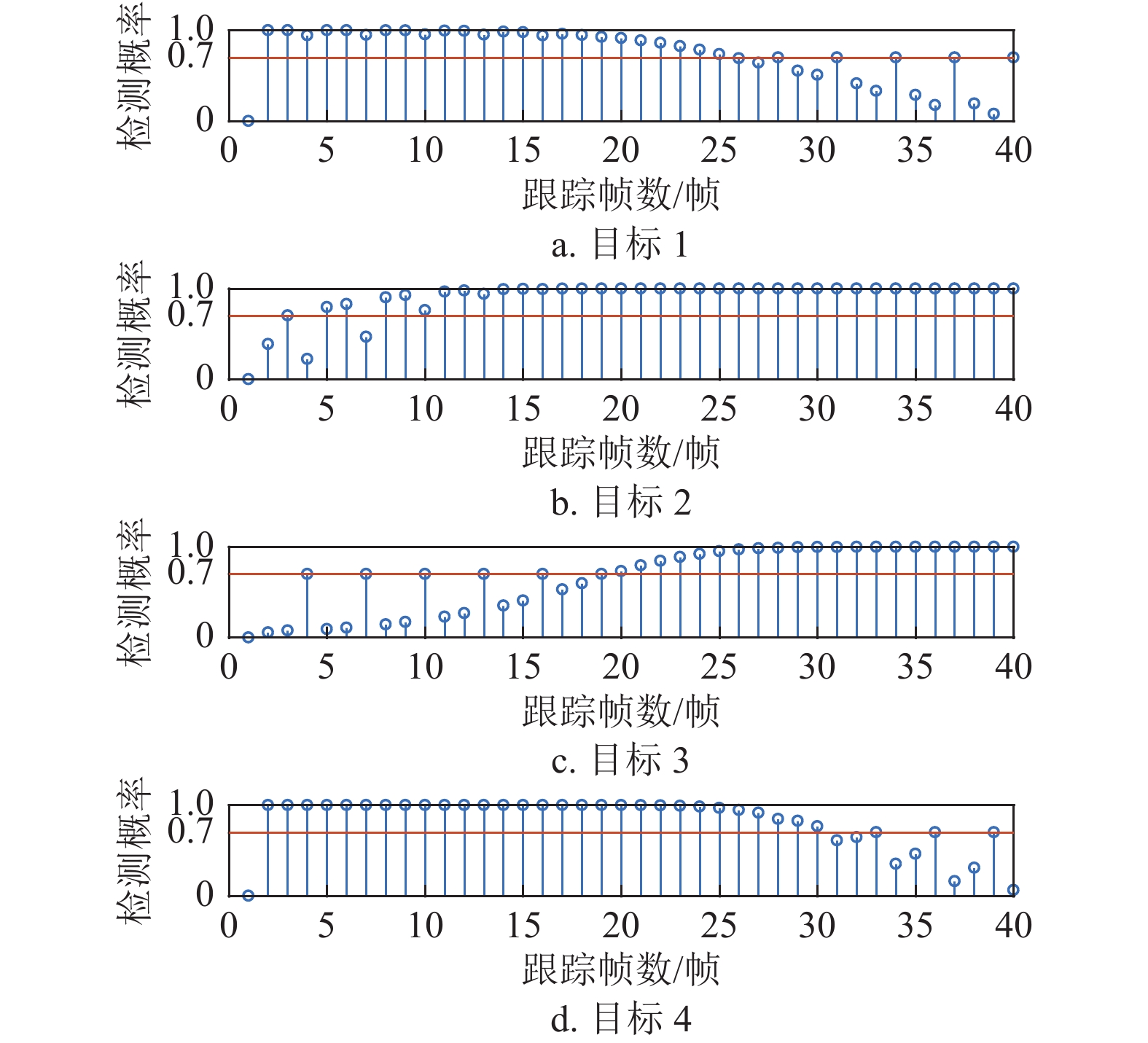
图3给出了SCPA算法优化得到的归一化功率分配方案(即功率与系统总功率的比值),栅格中的颜色表示各目标所分配的归一化功率的值。同时,图4给出了由SCPA算法优化下各目标的检测概率。可以发现,在跟踪初始阶段,目标3位于雷达系统的远区,此时目标3需要更多的功率以获得可靠的检测。从图4中可以注意到,在跟踪初始阶段,目标3的检测性能处于一个较低的水平。此时,为了避免目标在3帧内未被雷达系统有效检测而引发航迹中断,雷达系统分配给目标3的功率每隔两帧会有大幅度提升,如在第4、7、10、13、16帧,如图3所示。
随着系统分配大量功率,目标3在第4、7、10、13、16帧的检测概率达到了检测概率阈值,因此避免了航迹中断,如图4所示。而在跟踪过程后期,目标1和4运动至雷达系统远区,因此需要更多的功率以保证可靠检测。从图3中可以发现,在跟踪后期,为目标1、4分配的功率也是每隔两帧就会大幅提升,从而使检测概率达到阈值,避免航迹中断。这也对应于图4中目标1、4的检测概率。
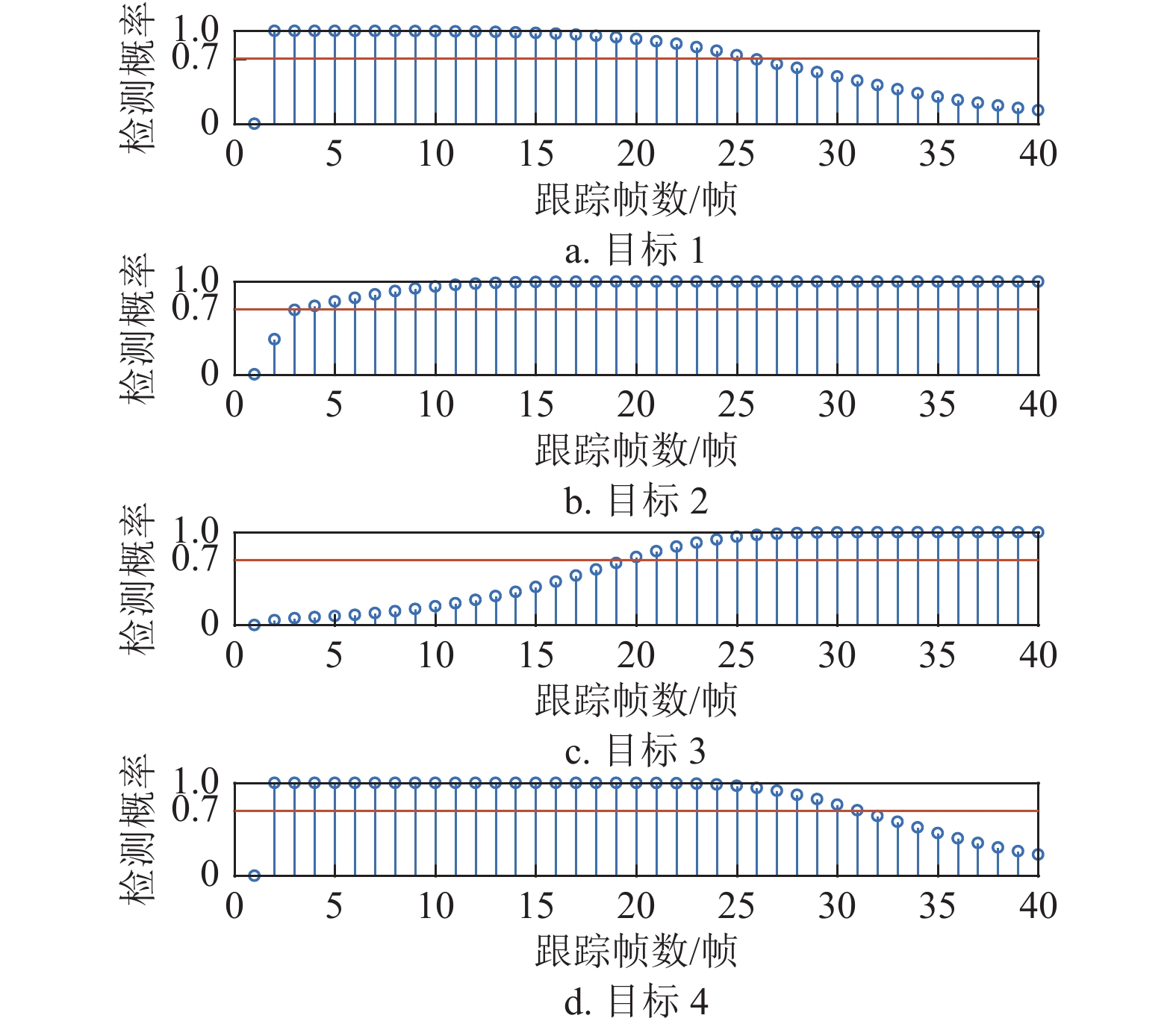
图5给出了FPA算法优化后的各目标检测概率。从图5中可以看出,由于FPA算法没有考虑检测不确定性,因此FPA优化的结果航迹中断现象非常严重。如前所述,跟踪前期的目标3和跟踪后期的目标1、4均位于雷达系统的远区,此时均匀分配的功率无法满足有效检测的需要。因此,目标1、3、4在相对应的阶段有相当长的时间,检测性能较差,因此航迹中断现象严重。而由于考虑了目标的检测不确定性,提出的SCPA算法可以保证所有目标跟踪全阶段航迹不中断,目标航迹质量高。
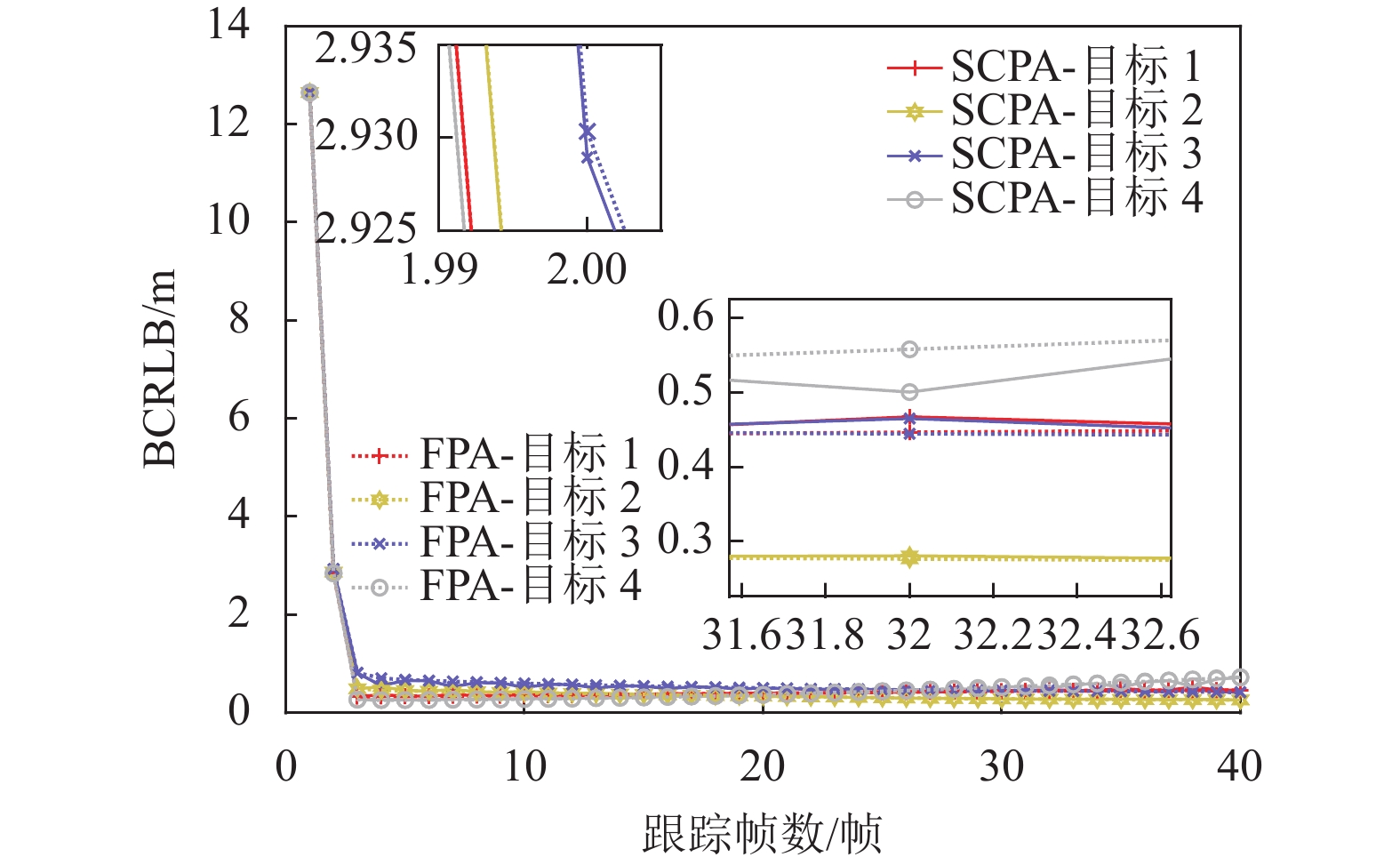
图6给出了两种算法的BCRLB,为300次蒙特卡洛实验平均结果。可以看出,两种算法优化后目标的BCRLB很接近,说明在保证航迹连续性的同时,SCPA算法可以保证良好的系统跟踪性能。因此,仿真结果表明所提SCPA算法的有效性。
4. 结 束 语
本文基于凸优化方法,将功率优化问题中的复杂约束进行拆分处理,提出了一种自约束功率分配算法,且所提算法具有可推广性。通过多组仿真实验可以看出,该算法可以通过对雷达系统功率资源的优化配置,在保证航迹连续性的同时,保证良好的系统跟踪性能。
-
[1] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823-838. DOI: 10.1109/TSP.2005.862813
[2] FISHLER E, HAIMOVICH A, BLUM R S, et al. Performance of MIMO radar systems: Advantages of angular diversity[C]//Conference Record of the 38th Asilomar Conference on Signals, Systems and Computers. Pacific Grove: IEEE, 2004: 305-309.
[3] HAIMOVICH A M, BLUM R S, CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2007, 25(1): 116-129.
[4] GODRICH H, PETROPULU A P, POOR H V. Power allocation strategies for target localization in distributed multiple-radar architectures[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3226-3240. DOI: 10.1109/TSP.2011.2144976
[5] XIE M C, YI W, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2017, 66(3): 729-743.
[6] YI W, YUAN Y, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602-1617. DOI: 10.1109/TSP.2020.2976587
[7] YAN J K, JIU B, LIU H W, et al. Prior knowledge-based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter[J]. IEEE Transactions on Signal Processing, 2014, 63(2): 512-527.
[8] FARINA A, RISTIC B, TIMMONERI L. Cramér-Rao bound for nonlinear filtering with Pd<1 and its application to target tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(8): 1916-1924. DOI: 10.1109/TSP.2002.800411
[9] WANG Y, ZHOU T, YI W, et al. A GDOP-based performance description of TOA localization with uncertain measurements[J]. Remote Sensing, 2022, 14(4): 910. DOI: 10.3390/rs14040910
[10] YAN J K, PU W Q, ZHOU S H, et al. Collaborative detection and power allocation framework for target tracking in multiple radar system[J]. Information Fusion, 2020, 55: 173-183. DOI: 10.1016/j.inffus.2019.08.010
[11] ZHANG H W, XIE J W, SHI J P, et al. Sensor scheduling and resource allocation in distributed MIMO radar for joint target tracking and detection[J]. IEEE Access, 2019, 7: 62387-62400. DOI: 10.1109/ACCESS.2019.2916334
[12] 何友. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2013. HE Y. Radar data processing with applications[M]. Beijing: Publishing House of Electronics Industry, 2013.
[13] BOYD S, VANDENBERGHE L. Convex optimization [M]. Cambridge: Cambridge University Press, 2004.
[14] WHITLEY D. A genetic algorithm tutorial[J]. Statistics and Computing, 1994, 4(2): 65-85.

 ISSN
ISSN 


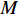
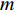

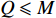
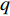
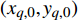


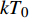
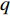
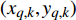
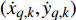
 下载:
下载: