Analysis of the Self-Interference Cancellation Capacity in Communication under Jamming Links
-
摘要: 针对基于射频干扰对消的扰中通系统,本文研究了采用多抽头射频干扰重建技术可获得的自干扰抑制度,给出了抽头数为2的自干扰消除器的解析结构,并分析了干扰消除效果与信号带宽和抽头数的关系。数值分析与计算机仿真结果表明:干扰消除能力随信号带宽增大而减弱,随抽头数增加而提升,对于100 MHz带宽信号,6抽头射频对消器在S频段可提供约70 dB的自干扰消除能力。Abstract: For a radio frequency (RF) interference cancellation based communication under jamming system, this paper investigates the achievable self-interference (SI) cancellation capacity of the multi-tap RF interference reconstruction scheme, derives the corresponding signal model in present of two taps, and analyzes the relationship between the cancellation capacity and the SI bandwidth as well as the tap number. The numerical analysis and simulations show that the achievable cancellation capacity decreases as the SI bandwidth increases and 6 taps can degrade an S-band 100-MHz bandwidth SI by about 70 dB.
-
战场环境“扰中通”链路的特征是在相同的时频资源上,干扰敌方通信设备的同时建立我方的有效无线通信[1]。由于收发使用相同(或邻近)的载波频率,己方蓄意辐射的大功率干扰会严重压制通信信号,甚至阻塞接收机前端,导致通信链路无法正常工作。因此,实现“扰中通”的核心是抑制已知的强干扰。
针对自干扰抑制技术的研究[2-4]大多聚焦于数字域信号处理,这类方法并不适宜“扰中通”场景。由于干扰机释放的干扰功率远高于通信接收机工作电平,即使接收机前端不被阻塞,ADC也难以提供足够的动态范围实现数字化。因此,扰中通系统必须首先在射频前端完成自干扰抑制,确保残余干扰功率符合ADC动态范围的约束,再进一步实施数字干扰抑制以消除残余干扰。
为实现射频自干扰抑制,文献[5]采用单独的发射通道产生自干扰信号,在接收机前端实行干扰对消。由于不能消除发射机噪声,该方法仅能提供约33 dB自干扰抑制度。文献[6]提出采用一定间距的两根发射天线,其合成方向图在接收天线处形成零陷。该方法对天线布局要求较高,且不能处理宽带干扰。文献[7-8]利用巴伦(Balun)完成发射信号取反以对消干扰,该方法可支持宽带干扰消除,但需要在射频实现高精度时延对齐,工程实现难度较大。文献[9]提出采用多抽头延时线,通过对不同抽头的幅度加权实现信号的内插重建,避免了对高精度延时调节的需求;文献[10]通过实验设计,进一步验证了该方法的有效性;然而,上述研究均未给出干扰抑制能力的理论上界分析:即不考虑工程实现损耗,给定信号带宽和重建干扰的抽头数,实现最大干扰抑制度[9]。
因此,本文首先描述了一种基于多抽头干扰重建的“扰中通”系统,其次,分析了干扰消除效果与信号带宽时延以及抽头数的关系,并给出了抽头数为2时干扰抑制度的解析表达式,最后通过对数值计算和仿真结果的分析,得出对工程实现有意义的结论。
1. 系统模型
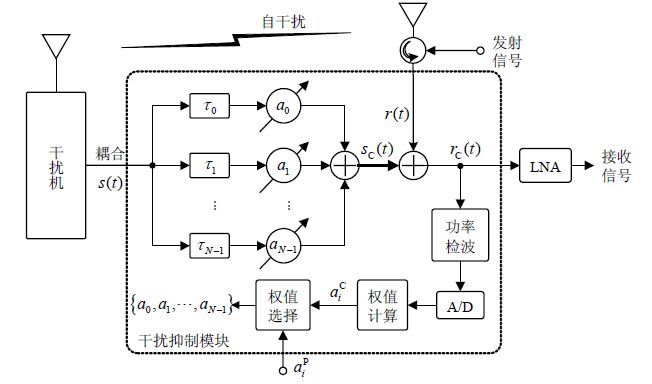
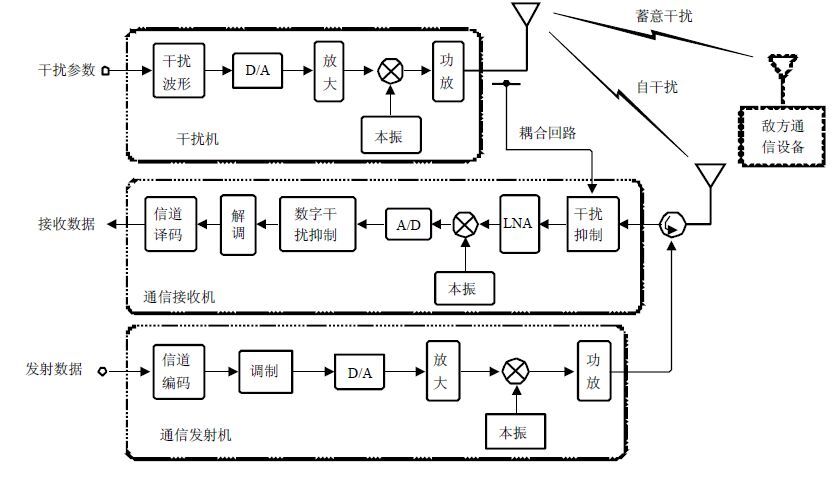
图 1给出了基于射频自干扰消除的扰中通系统模型。系统由干扰机、通信发射机和通信接收机3部分组成。假设通信接收机与干扰机在相同时间、相同频率上工作,接收通道除了会接收到远端的通信信号,即有用信号rU(t),还会收到本地发射信号的自干扰rI(t),rI(t)的功率通常比强若干数量级。干扰抑制模块位于通信接收机低噪声放大器(LNA)前级,该模块有两个射频输入信号,分别来自接收天线和耦合回路,其输出为干扰抑制后的射频信号。
接收机收到的信号可表示为:
$$r(t) = {h_{\text{J}}}s(t - {\tau _{\text{J}}}) + {r_{\text{U}}}(t) + n(t)$$ (1) 式中,s(t)为干扰信号;n(t)为接收机噪声;为自干扰信号幅度;τ(t)为传播时延。假设干扰机天线和接收机天线存在直射路径(LOS),且直射径信号功率远高于其他反射路径,则直射径信号是导致ADC阻塞的主要原因,射频自干扰抑制只需要消除直射径自干扰。
采用如图 2所示的射频自干扰抑制模型。其中,τi是固定延时,增益调节模块由可变增益放大器和衰减器组成,ai是增益调节参数, $i = 0,1, \cdots ,N - 10$ 。重建信号可以表示为:
s(t)与r(t)合路,完成自干扰消除,rc(t)为干扰对消的输出,可以表示为:
$$\eqalign{ & {r_{\text{C}}}(t) = r(t) + {s_{\text{C}}}(t) = \cr & {r_{\text{U}}}(t) + {s_{\text{R}}}(t) + n(t) \cr} $$ (3) 式中, ${s_{\text{R}}}(t) = {h_{\text{J}}}s(t - {\tau _{\text{J}}}) - {s_{\text{C}}}(t)$ 定义为残余干扰。干扰抑制的准则是最小化sR(t)的能量。一般情况下可以认为随机过程rU(t)、s(t)和n(t)之间相互独立,所以残余干扰能量rc(t)最小等价于使能量最小。给定干扰抑制目标信号的基带信号带宽B和固定抽头延时 ${\tau _i},{\text{ }}i = 0,1, \cdots ,N - 1$ ,干扰抑制的目标函数为选择 ${a_0},{a_1}, \cdots ,{a_{N - 1}}$ ,使Λ最小:
$$\Lambda = \mathop {\min }\limits_{{a_0},{a_1}, \cdots ,{a_{N - 1}}} \frac{1}{T}\int_T {{{\left| {{r_{\text{C}}}(t)} \right|}^2}{\text{d}}t} $$ (4) 式中,T为能量检测积分时间。显然Λ是目标带宽B、抽头数N、干扰时延τJ以τi及的函数。具体实施中增益调节参数的选择分3步进行:
1) (权值粗估计):干扰设备启动后射频前端处于饱和状态,接收通道被阻塞。此时利用射频功率检波器,根据梯度迭代最陡下降算法,可得到权值粗估计aic。基于aic实现干扰抑制后,阻塞消除,信号可以被A/D正常采样和量化。
2) (权值精估计):步骤1)基于射频功率检波只能得到初步的加权值。精确估计的权值aiP在图 1所示数字干扰抑制模块中计算得到,并反馈到射频干扰抑制模块。
3) (权值选择):权值选择模块根据射频及ADC阻塞情况,从aic、aiP两组权值中选择使用。
本文将首先针对的情况,推导干扰抑制度与B及τi的解析关系;再通过计算机仿真评估N>2的干扰抑制效果。用ROPT表示干扰抑制度的理论上界,其定义是:假设射频器件具有理想的数字特征(即忽略电缆时延误差、幅度调整误差、放大器线性度等工程因素),进入接收天线的自干扰能量与残余干扰能量之比的最大值。
2. 干扰抑制度计算
定义干扰的射频信号为:
$$s(t) = \operatorname{Re} \left\{ {{s_{\text{b}}}(t){{\text{e}}^{{\text{j}}2{\pi }{f_{\text{0}}}t}}} \right\}$ \end{document$ (5) 式中,sb(t)为复基带;N=2为载波频率。当时,干扰重建可以看作由两个不同幅度、相位的矢量,按照矢量加减法则(平行四边形法则)合成目标矢量的过程,则残余干扰可以表示为对消目标与重建干扰之差:
$$\eqalign{ & {s_{\text{R}}}(t) = {h_{\text{J}}}s(t - {\tau _{\text{J}}}) - ({a_0}s(t - {\tau _0}) + {a_1}s(t - {\tau _1})) = \cr & \operatorname{Re} \{ {h_{\text{J}}}{s_{\text{b}}}(t - {\tau _{\text{J}}}){{\text{e}}^{{\text{j}}2{\pi }{f_{\text{0}}}(t - {\tau _{\text{J}}})}} - {a_0}{s_{\text{b}}}(t - {\tau _{\text{0}}}){{\text{e}}^{{\text{j}}2{\pi }{f_{\text{0}}}(t - {\tau _{\text{0}}})}} - \cr & {a_1}{s_{\text{b}}}(t - {\tau _{\text{1}}}){{\text{e}}^{{\text{j}}2{\pi }{f_{\text{0}}}(t - {\tau _{\text{1}}})}}\} \cr} $$ (6) sR(t)的傅里叶变换为:
$$\eqalign{ & {S_{\text{R}}}(f) = \frac{1}{2}({S_{\text{b}}}(f - {f_0}) + S_{\text{b}}^*( - f - {f_0})) \times \cr & ({h_{\text{J}}}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{J}}}}} - {a_0}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{0}}}}} - {a_1}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{1}}}}}) \cr} $$ (7) 残余干扰的能量可以在频域计算为:
$$\eqalign{ & {E_{\text{R}}} = \int\limits_{2B} {{{\left| {{S_{\text{R}}}\left( f \right)} \right|}^2}{\text{d}}f} = \cr & {\text{ }}\int\limits_{2B} {{{\left| {\frac{1}{2}({S_{\text{b}}}(f - {f_0}) + S_{\text{b}}^*( - f - {f_0})) \times ({h_{\text{J}}}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{J}}}}} - {a_0}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{0}}}}} - {a_1}{{\text{e}}^{ - {\text{j}}2{\pi }f{\tau _{\text{1}}}}})} \right|}^2}{\text{d}}f} \cr} $$ (8) 式中,2B表示射频带宽。为便于直观表示ROPT与B和τi的关系,设sb(t)在目标带宽B内具有平坦的幅频响应Sb,且根据文献[10],τi取值应满足奈奎斯特采样定理,不妨设 ${\tau _0} - {\tau _1} = 1/(4B)$ 且 ${\tau _0} < {\tau _J} < {\tau _1}$ ,则式可以进一步表示为:
$$\eqalign{ & {E_{\text{R}}} = \int\limits_{2B} {{{\left| {{S_{\text{R}}}(f)} \right|}^2}{\text{d}}f} = \frac{{BS_{\text{b}}^2}}{2}\left( {h_{\text{J}}^2 + a_0^2 + a_1^2 - } \right. \cr & 2{a_0}{h_J}\cos \frac{{\eta {\pi }}}{2}{\text{sinc}}\frac{{\eta {\pi }B}}{{4{f_0}}} - \left. {2{a_1}{h_J}\sin \frac{{\eta {\pi }}}{2}{\text{sinc}}\frac{{(1 - \eta ){\pi }B}}{{4{f_0}}}} \right) \cr} $$ (9) 式中, $\eta = \frac{{{\tau _J} - {\tau _0}}}{{{\tau _1} - {\tau _0}}}$ 为时延比例因子, $0 < \eta < 1$ 。
分别计算ER对a0、a1的一阶偏导数,得:
$$\left\{ \matrix{ {{\partial {E_{\rm{R}}}} \over {\partial {a_0}}} = BS_{\rm{b}}^2\left( {{a_0} - {h_{\rm{J}}}\cos {{\eta \pi } \over 2}{\rm{sinc}}{{\eta \pi B} \over {4{f_0}}}} \right) = 0 \hfill \cr {{\partial {E_{\rm{R}}}} \over {\partial {a_1}}} = BS_{\rm{b}}^2\left( {{a_1} - {h_{\rm{J}}}\sin {{\eta \pi } \over 2}{\rm{sinc}}{{(1 - \eta )\pi B} \over {4{f_0}}}} \right) = 0 \hfill \cr} \right.$$ (10) 求解方程组,得抽头加权系数a0和a1的最优解:
$$\left\{ \matrix{ {a_0} = {h_{\rm{J}}}\cos {{\eta \pi } \over 2}{\rm{sinc}}{{\eta \pi B} \over {4{f_0}}} \hfill \cr {a_1} = {h_{\rm{J}}}\sin {{\eta \pi } \over 2}{\rm{sinc}}{{(1 - \eta )\pi B} \over {4{f_0}}} \hfill \cr} \right.$$ (11) 将式代入式,可得残余干扰能量的最小值ERmin为:
$$\eqalign{ & E_{\text{R}}^{\min } = \frac{{h_{\text{J}}^2BS_{\text{b}}^2}}{2}\left[ {1 - {{\left( {\cos \frac{{\eta {\pi }}}{2}{\text{sinc}}\frac{{\eta {\pi }B}}{{4{f_0}}}} \right)}^2} - } \right. \cr & \left. {{{\left( {\sin \frac{{\eta {\pi }}}{2}{\text{sinc}}\frac{{(1 - \eta ){\pi }B}}{{4{f_0}}}} \right)}^2}} \right] \cr} $$ (12) 由式可得,以对数形式表示的自干扰抑制度ROPT为:
$$\eqalign{ & {R_{{\rm{OPT}}}} = - 10\lg (E_{\rm{R}}^{\min }/E_{\rm{R}}^{\min }{E_{\rm{J}}}) = \cr & - 10\lg \left\{ {1 - {{\left( {\cos {{\eta \pi } \over 2}{\rm{sinc}}{{\eta \pi B} \over {4{f_0}}}} \right)}^2}} \right. \cr & \left. { - {{\left( {\sin {{\eta \pi } \over 2}{\rm{sinc}}{{(1 - \eta )\pi B} \over {4{f_0}}}} \right)}^2}} \right\} \cr} $$ (13) 式中, ${E_{\text{J}}} = \frac{{h_{\text{J}}^2BS_{\text{b}}^2}}{2}$ 是自干扰能量; ${\rm{sinc(}}x{\rm{)}} = \sin (x)/x$ 为SINC函数。
3. 数值分析及仿真
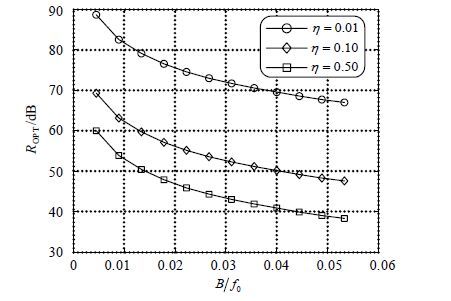
由式(13)可见,ROPT与(B/f0)以及时延比例因子有关,称为相对带宽。图 3和图 5分别根据式绘出了与和与之间的关系。
由图 3可见,ROPT随(B/f0)增加单调下降,说明了自干扰抑制能力随(B/f0)增加而减弱,该结论与文献[7-10]的实验验证结果相符;从图 3中还可以看出,自干扰抑制能力与时延比例因子η有关,η越小,自干扰抑制能力越强。
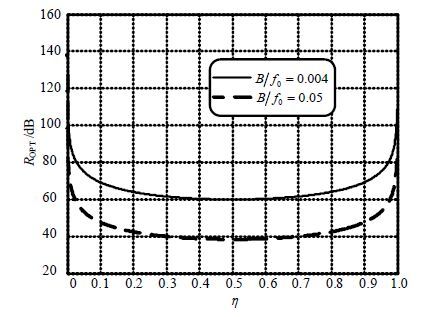
图 4进一步验证了上述结果:一方面,η=0.5时干扰抑制能力最弱,且对不同信号带宽该结论都成立;另一方面,当η→0或1时,ROPT将趋于无穷大。这是因为当η=0(或1)时,时延τJ=τ0(或τ1),自干扰信号可以被精确重建。
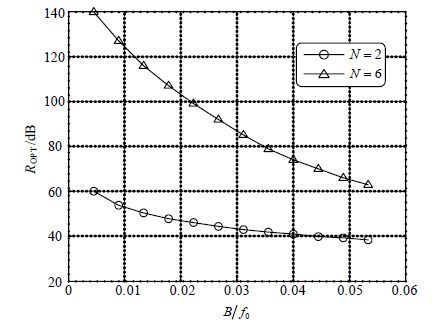
图 5给出了N=6抽头数N = 6,不同B/f0下自干扰消除能力的计算机仿结果,并与N = 2的情况进行了对比。仿真参数设置满足如下约束条件: ${\tau _i} - {\tau _{i - 1}}1/\left( {4B} \right)$ 且τJ位于两个相邻抽头延时之间1/2处(相应于图 4中τ=0.5的情况)。根据图 5的仿真结果可以得到如下3个结论。
1) 自干扰消除能力随抽头数增加而增强,其物理意义是:多抽头干扰重建可以看作是更高维度的矢量合成,越大,干扰重建精度越高。考虑f0=2 400MHz的典型S频段工程应用,对于100 MHz带宽信号,6抽头射频对消器可提供约70dB的自干扰消除能力。
2) N=6的曲线具有更大的斜率,二者性能随B/f0增加趋于相近。对于该现象,结合式的结果可初步解释如下:当B/f0较小时,SINC衰减较小,抽头数量带来的重建精度增加占主导地位,因此不同抽头数的ROPT性能差距较大。然而,当干扰带宽增加时,SINC衰减引起的ROPT减小开始逐渐占据主要地位,且SINC衰减随B/f0增加进一步加剧,最终导致不同抽头数的ROPT性能趋于相近。
3) 不同抽头数时,ROPT曲线的单调性不变。
4. 结论
针对“扰中通”链路设备同时同频收发的特征,本文描述了一种采用多抽头射频干扰重建技术的自干扰抑制系统,阐述了系统的工作原理。推导了抽头数为2时最优干扰抑制度的解析表达式,结合计算机仿真分析了干扰抑制能力随带宽和抽头数变化规律的原因,得到如下结论:首先,射频自干扰抑制度随干扰带宽增加而减小,其变化规律具有单调性;其次,增加抽头数量可以提升干扰抑制能力,其效果也随信号带宽增加而减弱。本文在分析和仿真过程中仅考虑了直射径的情况。针对多径环境射频自干扰抑制的性能分析将是下一阶段的研究方向。
-
[1] Exelis Inc. EA-18G interference cancellation system (INCANS)[EB/OL].[2015-02-13]. http://www.exelisinc.com.
[2] LEE Y J, LEE J B, SUNG I P, et al. Feedback cancellation for T-DMB repeaters based on frequency-domain channel estimation[J]. IEEE Transactions on Broadcasting, 2011, 57(1):114-120.
[3] GOLLAKOTA S, KATABI D. ZigZag decoding:Combating hidden terminals in wireless networks[C]//SIGCOMM'08:Proceedings of the ACM SIGCOMM 2008 Conference on Data Communication. New York, ACM, 2008:159-170.
[4] HALPERIN D, ANDERSON T, WETHERALL D. Taking the sting out of carrier sense:Interference cancellation for wireless lans[C]//MobiCom'08:Proceedings of the 14th ACM International Conference on Mobile Computing and Networking. New York:ACM, 2008:339-350.
[5] DUARTE M, SABHARWAL A. Full-duplex wireless communications using off-the-shelf radios:Feasibility and first results[C]//45th Asilomar Conference on Signals, Systems, and Components. CA, USA:IEEE, 2010.
[6] CHOI J I, JAIN M, SRINIVASAN K, et al. Achieving single channel, full duplex wireless communication[C]//Proc 2010 ACM MobiCom. Chicago, IL:ACM, 2010:1-12.
[7] JAIN M, CHOI J I, KIM T M, et al. Practical, real-time, full duplex wireless[C]//17th Annual International Conference on Mobile Computing and Networking (MobiCom'11). NewYork:[s.n.], 2011.
[8] HONG S, MEHLMAN J, KATTI S. Picasso:Flexible RF and spectrum slicing[C]//Proc 2012 ACM SIGCOMM. Helsinki, Finland:ACM, 2012:37-48.
[9] MCMICHAEL J G, KOLODZIEJ K E. Optimal tuning of analog self-interference cancellers for full-duplex wireless communication[C]//15th Annual Allerton Conference. Illinois, USA:[s.n.], 2012.
[10] BHARADIA D, MCMILIN E, KATTI S. Full duplex radios[C]//Proc 2013 ACM SIGCOMM. Hong Kong, China:ACM, 2013:375-386.
-
期刊类型引用(2)
1. 郭文博,林朗,赵宏志,唐友喜. 频谱共生干扰主动抑制技术研究. 中国科学:信息科学. 2022(10): 1915-1928 .  百度学术
百度学术
2. 樊小琴. 一种近场同频干扰主动抵消架构. 通信技术. 2017(12): 2684-2687 .  百度学术
百度学术
其他类型引用(2)

 ISSN
ISSN 


 下载:
下载: