Maximum Likelihood Multiple Symbol Differential Demodulation Algorithms for Underwater VLF MSK Signal
-
摘要: 水下甚低频(VLF)最小频移键控(MSK)信号受脉冲噪声、海水衰减和海面起伏的共同影响。为了降低对相位同步的要求,提高解调算法的适应性,该文研究了水下甚低频MSK信号的差分解调算法,建立了甚低频MSK调制信号在海水中的传播模型。考虑脉冲噪声处理算法的影响,基于最大似然(ML)原理推导了水下甚低频MSK信号多符号差分解调算法。仿真结果表明:水下甚低频MSK信号最大似然多符号差分解调算法在相位同步下可获得逼近相干解调的性能,在相位不同步下可获得优于相干解调的性能,具有显著的优势。Abstract: Underwater very low frequency (VLF) minimum shift keying (MSK) signals are distorted by the impulsive noise, the propagation attenuation of sea water and the fluctuation of sea wave. In order to reduce the requirement for carrier phase synchronization and improve the robustness of demodulation algorithm, the differential demodulation algorithm of the underwater VLF MSK signal is investigated in this paper. The propagation attenuation of sea water is first modeled. By considering the impact of suppressing impulsive noise, the multiple-symbols differential demodulation of the underwater VLF MSK signal is then derived based on the principle of maximum likelihood (ML) detection. Extensive simulation results show that the performance of the ML multiple-symbols differential demodulation algorithm can closely approach that of the coherent demodulation algorithm if the carrier phase is recovered and a relative large amount of symbols are utilized. On the other hand, the differential demodulation algorithm is superior to the coherent demodulation algorithm if the carrier phase is not recovered.
-
Keywords:
- differential demodulation /
- impulsive noise /
- MSK /
- sea wave /
- VLF
-
由于电磁波在水下传播时的衰减率随着频率的增大而显著增加,岸基与水下潜器通信系统一般采用频段范围为3~30 kHz[1]的甚低频。为了兼顾能量效率和频谱效率,甚低频岸基至水下潜器通信通常采用MSK信号[1]。为了叙述简洁,本文将其称为水下甚低频MSK信号。
甚低频MSK信号传播到水下的过程中会受海水衰减和天电噪声的共同影响。一方面,甚低频电磁波在海水中传播时具有较大的衰减率(约为1.9~6dBm)[2],同时,甚低频岸基与水下潜器通信系统通常的接收深度为10 m左右,而海面的起伏严重时可达几米,因此必须考虑海浪起伏对信号的影响[1]。另一方面,水下甚低频MSK信号还会受到天电噪声的干扰,天电噪声是典型的脉冲噪声[3]。由于海水对甚低频信号具有显著的低通滤波特性,脉冲噪声经过海水传播后在时域上会被展宽[4],不利于对脉冲噪声的处理,必须进行准确的海洋补偿滤波。由于上述两方面因素的影响,需要精确同步的相干解调算法,实现起来比较复杂,所以水下甚低频MSK信号通常采用非相干的差分解调算法[5]。
现有的水下甚低频MSK信号差分解调一般采用简单的两符号次优解调方法,性能不佳[1]。为此,本文综合考虑脉冲噪声、白噪声和海洋补偿滤波器对水下甚低频MSK信号的影响,基于最大似然原理,推导多符号水下甚低频MSK信号差分解调算法。
1. 系统模型
1.1 海水中电波的传播特性
电磁波在传播过程中,满足Maxwell方程组及其辅助方程。假设所研究的电磁波为简谐波,波的传播方向竖直向下,则其对时间的关系为ejωt,ω为信号角频率。令导电介质中的电荷体密度为零,即ρ=0,将其代入辅助方程,并将辅助方程代入到Maxwell方程组,得海水中Maxwell方程组为[6]:
$$ \left\{ \begin{gathered} \nabla \times {\mathbf{H}} = \sigma {\mathbf{E}} + j\omega {\mathbf{D}} \hfill \\ \nabla \times {\mathbf{E}} = - j\omega {\mathbf{B}} \hfill \\ \nabla {\mathbf{D}} = 0 \hfill \\ \nabla {\mathbf{B}} = 0 \hfill \\ \end{gathered} \right. $$ (1) 求解式可得海水中电磁波的衰减规律为[1]:
$$ \left\{ {\begin{array}{*{20}{l}} {H(z) \approx H(0)2{e^{ - \alpha z}}2{e^{ - j\beta z}}} \\ {E(z) \approx E(0)2{e^{ - \alpha z}}2{e^{ - j\beta z}}} \end{array}} \right.{\text{ }} $$ (2) 式中,E(z)和H(z)分别表示水下离海面深度为z的接收点的水平电场和磁场;E(0)和H(0)分别表示海面上的水平电场和磁场;α和β分别为衰减常数和相移常数,满足$\alpha = \beta = \sqrt {\omega \mu \sigma /2} $。本文中,取海水的导电率σ=4 S/m,磁导率$\mu = 4{\text{π }} \times {10^{ - 7}}{\text{ }}H/m $[7]。
1.2 海浪模型
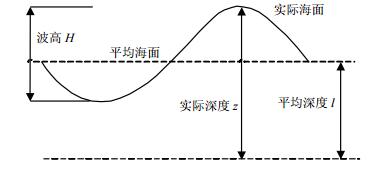
接收深度的变化对信号的幅度、相位和脉冲噪声的补偿存在影响[1, 7]。海浪对接收深度的影响如图 1所示。显然,海面的起伏会使水下接收天线的深度发生变化。
本文使用常用的线性海浪模型[8]:
$$ \zeta (t) = \sum\limits_{i = 1}^\infty {{a_i}\cos ({\omega _i}t + {\varepsilon _i})} $$ (3) 式中,ai为振幅;ωi为角频率;εi为初始相位,服从0~2π的均匀分布,即:εi~U(0, 2π)。线性海浪模型认为海浪是平稳正态过程,且具有各态历经性,由无限多个不同波幅、不同频率的组成波叠加而成,并且这些组成波是随机且互相独立的,叠加的结果也具有各态历经性的平稳正态过程。本文借助ITTC(international towing tank conference)[9]参数谱海浪谱(海浪内部结构)来对海浪进行描述,由于海浪谱与叠加海浪模型的振幅之间满足:
$$ {S_\zeta }({\omega _i})\Delta \omega = \frac{1}{2}a_i^2 $$ (4) 则简化的海浪模型波面高度为:
$$ \zeta (t) = \sum\limits_{i = 1}^\infty {\sqrt {2{S_\zeta }({\omega _i})\Delta \omega } } \cos ({\omega _i}t + {\xi _i}) $$ (5) 1.3 海水对脉冲噪声的影响和处理
海水信道可近似为一个低通滤波,在可以忽略移位电流的情况下,其复传递函数与接收点深度z处的水平电场和水平面水平磁场有关。海水的复传递函数为[7]:
$$ {W_O}(f,d) = {\left( {\frac{{j2\pi f\mu }}{\sigma }} \right)^{1/2}}\exp \left[ { - z{{(j2\pi f\mu \sigma )}^{1/2}}} \right] $$ (6) 式中,f是载波频率。
海水信道会使脉冲噪声的波形被展宽,尖锐程度锐减。这使得后续在对脉冲噪声进行处理后,信号中残留的噪声功率会大幅增加,严重影响系统性能。为此,需要对海水信道进行补偿。海洋补偿滤波器对海水低通特性补偿平衡,其幅频特性与海水的低通特性完全相反[7],脉冲噪声通过合适的海洋补偿滤波器后可恢复其脉冲特性。
1.4 脉冲噪声抑制
对脉冲噪声的抑制常用限幅器(clipper)[10]:
$$ {x_{clipper}} = \left\{ \begin{gathered} - C{\text{ }}x < - C \hfill \\ x{\text{ }}\left| x \right| \leqslant C \hfill \\ C{\text{ }}x > C \hfill \\ \end{gathered} \right. $$ (7) 式中,x为限幅器输入信号;xclipper为其输出信号。限幅器的门限c与脉冲噪声的强度、白噪声强度和信号幅度密切相关,最优门限可通过仿真实验得到。脉冲噪声通过限幅器后为准高斯噪声[11]。
1.5 接收信号模型
经过海水衰减、叠加脉冲和高斯白噪声的水下甚低频信号经过海洋补偿滤波和脉冲噪声预处理后,解调器输入端信号为:
$$ r(t) = s(t){e^{{\text{j}}\theta }}{{\text{e}}^{ - \alpha z - {\text{j}}\beta z}} + n(t) $$ (8) 式中,s(t)是发送信号;z是实际接收深度,服从N(l, (H/3)2)的正态分布,l是平均接收深度,H是波高;接收相偏θ~U(0, 2π);n(t)是高斯白噪声。
2.1 MSK信号
任意二进制全响应CPM信号可以表示为[12]:
$$ s(t) = \sqrt {\frac{{2{E_b}}}{T}} \sum\limits_i {{c_i}} g(t - iT) $$ (9) 式中,Eb是每比特信号的发送能量;1/T是比特速率;g(t)是持续时间为2T的有限时间冲击响应;{ci}是数据序列,数据ci与信息相位ϕi之间满足关系:
$$ {c_i} = {c_{i - 1}}{e^{j\pi h{\varphi _i}}} $$ (10) 对于MSK信号,h=1/2,g(t)可表示为:
$$ g(t) = \sin \left( {\frac{{\pi t}}{{2T}}} \right){u_{2T}}(t) $$ (11) 且ϕi=±1,式变为:
$$ {c_i} = {\text{j}}{c_{i - 1}}{\varphi _i} $$ (12) 水下甚低频信号接收模型为:
$$ r(t) = s(t){{\text{e}}^{{\text{j}}\theta }}{{\text{e}}^{ - \alpha z - {\text{j}}\beta z}} + n(t) $$ (13) 2.2 水下MSK最大似然差分解调
传统MSK差分解调利用前后两个码元的信息。从式~式可以发现:ϕk的变化范围与冲击响应$ {c_{k - 1}}g(t - kT + T) $(从(k-1)T持续到k+1)T)和${c_k}g(t - kT) $(从kT持续到k+2)T))有关。为了对ϕk作出判决,可至少选择3 bit的接收信号区间 $\left[{(k-1)T, (k + 2)T} \right] $。更精确一点,可以利用(2N+1)比特区间$ \left[{(k-N)T, (k + N + 1)T} \right] $对中间比特的信息相位ϕk作出判决。
基于最大似然原理,接收信号在相偏$\theta = \tilde \theta $、接收深度$ z = \tilde z $、数据向量${\tilde c_k} = \left[{{{\tilde c}_{k-N-1}}, {{\tilde c}_{k-N}}, \cdots, {{\tilde c}_{k + N}}} \right] $和接收信号模型式的条件下,似然函数为[2]:
$$ \begin{gathered} L(r(t)|{{\tilde c}_k}, \tilde \theta, \tilde z) = \\ \exp \left\{ { - \frac{1}{{2{N_0}}}\int_{{\text{ }}(k - N)T}^{{\text{ }}(k + N + 1)T} {\left| {r(t)} \right.} - {{\left. {s(t, {{\tilde c}_k}){{\text{e}}^{{\text{j}}\tilde \theta }}{{\text{e}}^{ - {\text{j}}\beta \tilde z - \alpha \tilde z}}} \right|}^2}{\text{d}}t} \right\} \\ \end{gathered} $$ (14) 将式(9)代入到式(14)中,得到:
$$ \begin{gathered} L(r(t)|{{\tilde c}_k}, \tilde \theta, \tilde z) = \exp \left\{ {\frac{1}{{{N_0}}}\sqrt {\frac{{2{E_b}}}{T}} \operatorname{Re} \left[{{{\text{e}}^{-{\text{j}}\beta \tilde z-\alpha \tilde z}}} \right.} \right. \times \\ {\text{ }}{{\text{e}}^{-{\text{j}}\tilde \theta }}\left. {\left. {\left( {\sum\limits_{i = k - N - 1}^{k + N} {\tilde c_i^ * \int_{(k - N)T}^{(k + N + 1)T} {r(t)} } g(t - iT){\text{d}}t} \right)} \right]} \right\} \\ \end{gathered} $$ (15) 记:
$$ \begin{gathered} F(r(t), {{\tilde c}_k}) = \sum\limits_{i = k - N - 1}^{k + N} {\tilde c_i^ * \int_{{\text{ }}(k - N)T}^{{\text{ }}(k + N + 1)T} {r(t)} } g(t - iT){\text{d}}t \\ \left\{ \begin{gathered} g(t) = {g_1}(t) + {g_2}(t - T) \hfill \\ {g_1}(t) = \sin \left( {\frac{{{\text{\pi }}t}}{{2T}}} \right){u_T}(t) \hfill \\ {g_2}(t) = \cos \left( {\frac{{{\text{\pi }}t}}{{2T}}} \right){u_T}(t) \hfill \\ \end{gathered} \right. \\ {x_n}(k) = \int_{{\text{ }}kT}^{{\text{ }}(k{\text{ + 1}})T} {r(t)} {g_n}(t - kT){\text{d}}t{\text{ }}n = 0, 1 \\ \end{gathered} $$ (16) 可得:
$$ \begin{gathered} F(r(t), {{\tilde c}_k}) = \tilde c_{k - N - 1}^ * {x_2}(k - N) + \\ \sum\limits_{i = k - N}^{k + N - 1} {\tilde c_i^ * \left[{{x_1}(i) + {x_2}(i + 1)} \right] + } \tilde c_{k + N}^ * {x_1}(k + N) \\ \end{gathered} $$ (17) 将$ L(r(t){\text{|}}{\tilde c_k}, \tilde \theta, \tilde z) $对θ积分得到:
$$ \begin{gathered} {L_1}(r(t)|{{\tilde c}_k}, \tilde z) = \\ {I_0}\left( {\frac{1}{{{N_0}}}\sqrt {\frac{{2{E_b}}}{T}} \left| {F(r(t), {{\tilde c}_k})} \right|{{\text{e}}^{ - {\text{j}}\beta \tilde z - \alpha \tilde z}}} \right) \\ \end{gathered} $$ (18) 式中,I0 (x)是零阶修正贝塞尔函数。再对z积分,于是求$ {L_2}(r(t){\text{|}}{\tilde c_k})$的最大值就转变为求$\left| {F(r(t), {{\tilde c}_k})} \right| $的最大值。定义:
$$ \begin{gathered} X = \left[{{x_1}(k-N), {x_2}(k-N), {x_1}(k-N + 1), } \right. \\ \left. {{x_2}(k - N + 1), \cdots, {x_1}(k + N), {x_2}(k + N)} \right] \\ \end{gathered} $$ (19) 相邻的2N个信息相位组成向量:
$$ \left\{ \begin{gathered} \tilde \varphi _{k - 1}^{( \leftarrow )} = ({{\tilde \varphi }_{k - N}}, {{\tilde \varphi }_{k - N + 1}}, \cdots, {{\tilde \varphi }_{k - 1}}) \hfill \\ \tilde \varphi _{k + 1}^{( \to )} = ({{\tilde \varphi }_{k + 1}}, {{\tilde \varphi }_{k + 2}}, \cdots, {{\tilde \varphi }_{k + N}}) \hfill \\ \end{gathered} \right. $$ (20) 结合式和式,并借助式和式的定义可得:
$$ \begin{gathered} F(X(k);\tilde \varphi _{k - 1}^{( \leftarrow )};{{\tilde \varphi }_k};\tilde \varphi _{k + 1}^{( \to )}) = {x_2}(k - N) + \\ \sum\limits_{i = k - N}^{k + N - 1} {\left[{{x_1}(i) + {x_2}(i + 1)} \right]} \exp \left( { - {\text{j}}\frac{{\text{\pi }}}{2}\sum\limits_{l = k - N}^i {{{\tilde \varphi }_l}} } \right){\text{ + }} \\ {x_1}(k + N)\exp \left( { - {\text{j}}\frac{{\text{\pi }}}{2}\sum\limits_{l = k - N}^{k + N} {{{\tilde \varphi }_l}} } \right) \\ \end{gathered} $$ (21) 又有:
$$ \begin{gathered} F(r(t), {{\tilde c}_k}) = \tilde c_{k - N - 1}^ * F(X(k);\tilde \varphi _{k - 1}^{( \leftarrow )};{{\tilde \varphi }_k};\tilde \varphi _{k + 1}^{( \to )}) \\ {\text{ }}\left| {\tilde c_{k - N - 1}^ * } \right| = 1 \\ \end{gathered} $$ (22) 利用式和判决反馈,水下MSK信号多符号差分解调算法的最终检测统计量为:
$$ {\hat \varphi _k} = \arg \mathop {\max }\limits_{{{\tilde \varphi }_k}, \tilde \varphi _{k + 1}^{( \to )}} \left\{ {\left| {F(X(k);\tilde \varphi _{k - 1}^{( \leftarrow )};{{\tilde \varphi }_k};\tilde \varphi _{k + 1}^{( \to )})} \right|} \right\} $$ (23) 3. 仿真分析
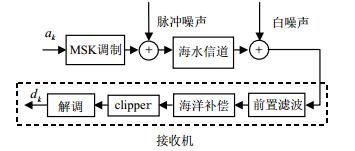
系统仿真链路如图 2所示,信息码元ak通过基带和载波调制变为MSK频带信号,然后叠加脉冲噪声,通过海水信道后叠加白噪声到达接收机前端,含脉冲噪声和白噪声的信号通过前置带通滤波器,然后进行海洋补偿恢复脉冲噪声的脉冲特性,再对脉冲噪声进行clipper处理,最后进行下变频和基带差分解调输出dk。
仿真中码元速率Rb=100b/s,载波频率fc=10 kHz,系统采样频率fs=80 kHz,水下接收深度10 m,Eb/N0是信号每比特能量与白噪声功率谱密度的比值,Clipper前端信号功率与脉冲噪声功率的比值η=0.1,Clipper的门限是根据不同强度的脉冲噪声和白噪声设置仿真获取。
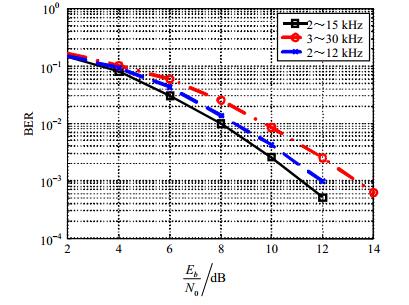
前置滤波器的带宽需要综合考虑脉冲噪声和白噪声对系统性能的影响。一方面,由于海洋补偿滤波器对高频白噪声有放大作用,前置滤波器的通带不能包含过多的高频部分;另一方面,前置滤波的带宽也不能过窄,过窄的带宽会使clipper对脉冲噪声的处理性能变差。为此,选取滤波器带宽2~15 kHz,2~12 kHz和3~30 kHz等不同范围,利用差分解调得到的仿真结果如图 3所示。从仿真结果可以看出:在当前的仿真条件下,前置滤波器的带宽选择2~15 kHz可以获得最好的性能。
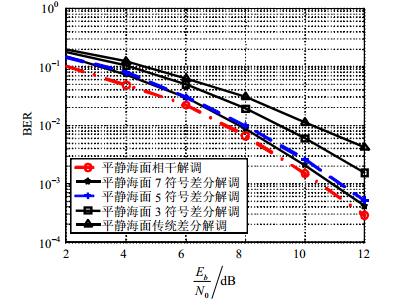
在平静海面的情况下,不同解调方法的误码曲线如图 4所示。从图中可以发现,传统的和3符号区间长度差分解调与相干解调相比性能损失超过2dB;5符号和7符号区间长度差分解调性能都可以逼近相干解调,而5符号区间差分解调计算上比7符号区间差分解调简单。所以在接收环境理想的情况下,5符号区间差分解调是一种比较理想的接收方式。
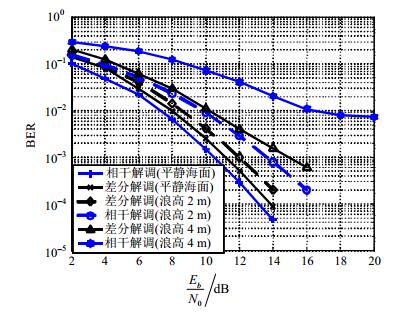
在未同步时,不同浪高的接收情况下,相干解调与5符号差分解调误码曲线如图 5所示。
图 5中,5差分解调表示的是5符号区间长度差分解调。可以发现:在浪高为2 m(接收环境较好)、BER=10-3的情况下,5符号区间长度差分解调比相干解调误码性能好大约2 dB;在浪高为4 m(接收环境恶劣)的情况下,随着Eb/N0的增大,5符号区间长度差分解调算法的误码率能达到10-3水平,而相干解调则达不到10-3水平。
这是由于:海浪的存在,会使得信号接收深度发生变化,使得信号相偏也在不断的变化,相干解调对相偏很敏感,由于不易于实现精确的相位同步,所以性能较差,而5符号区间长度差分解调对相偏不敏感,性能较好,这样降低了对相位同步的要求,能更好地适应不同的海面环境。
4. 结论
本文建立了甚低频MSK信号在海水中的传播模型,推导了水下MSK信号的多符号最大似然差分解调算法,仿真了不同海浪高度的情况下,水下甚低频MSK信号的性能。结果显示:5符号最大似然差分解调是用于水下甚低频MSK信号解调较好的方法。
-
[1] 陆洪, 潘威炎.海浪对水下甚低频最小频移键控信号解调的影响[J].电波科学学报, 2011, 26(4):731-734. http://www.cnki.com.cn/Article/CJFDTOTAL-DBKX201104019.htm LU Hong, PAN Wei-yan. Influence of sea waves on msk signal demodulation of VLF in the sea water[J]. Chinese Journal of Radio Science, 2011, 26(4):731-734. http://www.cnki.com.cn/Article/CJFDTOTAL-DBKX201104019.htm
[2] 左卫, 阚荣才, 任席闯.甚低频与超低频通信入水深度比较分析[J].舰船电子工程, 2014, 34(8):151-153. http://www.cnki.com.cn/Article/CJFDTOTAL-JCGC201408042.htm ZUO Wei, KAN Rong-cai, REN Xi-chuang. Comparison of depth of propagation in water between VLF and SLF[J]. Ship Electronic Engineering, 2014, 34(8):151-153. http://www.cnki.com.cn/Article/CJFDTOTAL-JCGC201408042.htm
[3] 施意, 张爽, 张昕.大气噪声对甚低频通信系统干扰仿真分析[J].通信技术, 2013, 46(9):32-34. http://www.cnki.com.cn/Article/CJFDTOTAL-TXJS201309010.htm SHI Yi, ZHANG Shuang, ZHANG Xin. Simulation and analysis of almospheric noise interference on VLF/LF communications[J]. Communication Technology, 2013, 46(9):32-34. http://www.cnki.com.cn/Article/CJFDTOTAL-TXJS201309010.htm
[4] 温东, 姜波, 刘翠海.超低频通信中海洋补偿滤波器设计[J].电讯技术, 2013, 53(1):77-81. http://www.cnki.com.cn/Article/CJFDTOTAL-DATE201301020.htm WEN Dong, JIANG Bo, LIU Cui-hai. Design of ocean compensation filter for super low frequency communication (SLF) communication[J]. Telecommunication Engineering, 2013, 53(1):77-81. http://www.cnki.com.cn/Article/CJFDTOTAL-DATE201301020.htm
[5] 芮国胜, 陈强, 田文飚, 等. MSK信号解调算法研究及其性能仿真比较[J].海军航空工程学院学报, 2015, 30(6):505-510. http://www.cnki.com.cn/Article/CJFDTOTAL-HJHK201506002.htm RUI Guo-sheng, CHEN Qiang, TIAN Wen-biao, et al. Demodulation algorithm reasearch and performance simulation of MSK signals[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(6):505-510. http://www.cnki.com.cn/Article/CJFDTOTAL-HJHK201506002.htm
[6] 郑强, 杨日杰.电磁波在海水中的传播特性研究[J].电声技术, 2013, 37(2):33-35. http://www.cnki.com.cn/Article/CJFDTOTAL-DSJS201302010.htm ZHENG Qiang, YANG Ri-jie. Propagation properties of electromagnetic wave in sea water[J]. Audio Engineering, 2013, 37(2):33-35. http://www.cnki.com.cn/Article/CJFDTOTAL-DSJS201302010.htm
[7] BERNSTEINS L, MCNEILL D, RICHER I. A signaling scheme and experimental receiver for extremely low frequency (ELF) communication[J]. IEEE Transactions on Communications, 1974, 22(4):508-528. DOI: 10.1109/TCOM.1974.1092208
[8] 聂卫东, 康凤举, 褚彦军, 等.基于线性海浪理论的海浪数值模[J].系统仿真学报, 2005, 17(5):1037-1039. http://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200505005.htm NIE Wei-dong, KANG Feng-ju, CHU Yan-jun, et al. Linear ocean wave simulation[J]. Journal of System Simulation, 2005, 17(5):1037-1039. http://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200505005.htm
[9] XU J B, BIAN X Q, FU M Y. Simulation and spectral analysis of sea wave[J]. Advanced Materials Research, 2012, 532-533(2):643-693. http://cn.bing.com/academic/profile?id=2084897937&encoded=0&v=paper_preview&mkt=zh-cn
[10] JAMES E E, ANDREW S G. Design of a sanguine noise processor based upon world-wide extremely low frequency (ELF) recordings[J]. IEEE Transactions on Communications, 1974, 22(4):528-539. DOI: 10.1109/TCOM.1974.1092215
[11] CHRISSAND A. Statistical analysis and modeling of low-frequency radio noise and improvement of low-frequency communications[D]. Stanford, USA:Stanford University, 1998.
[12] VITETTA G M, MENGALI U, MORELLI M. Differential detection algorithms for MSK signals over AWGN and frequency-flat Rayleigh fading channels[J]. IEEE Transactions on Communications, 2000, 47(12):1820-1827. http://cn.bing.com/academic/profile?id=2099812103&encoded=0&v=paper_preview&mkt=zh-cn
[13] GARY D B, PETER J M. Differential detection of duobinary CPFSK[J]. IEEE Transactions on Communications, 1987, 35(2):181-184. DOI: 10.1109/TCOM.1987.1096748
[14] WIKLUNDH K, FORS K, HOLM P. A log-likelihood ratio for improved receiver performance for VLF/LF communication in atmospheric noise[C]//34th Military Communications Conference. Tampa, USA:IEEE, 2015:1-6.
-
期刊类型引用(3)
1. 黄晓,陈奇东,刘睿,徐文璞,刘杨. 可用于导航定位的甚低频通信台信号相位测量技术研究. 全球定位系统. 2023(04): 75-80 .  百度学术
百度学术
2. 胥艳,陈鲁聪. MSK调制下的匹配滤波接受研究. 舰船电子工程. 2018(04): 35-39 .  百度学术
百度学术
3. 张丹丹,陈洪义,刘芳,徐琪,潘鸣. 基于MSK功率谱的巷道内宽度盲估计方法. 太赫兹科学与电子信息学报. 2017(04): 585-589 .  百度学术
百度学术
其他类型引用(8)

 ISSN
ISSN 


 下载:
下载: