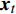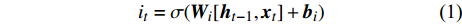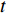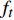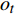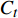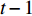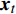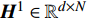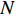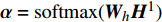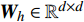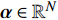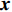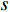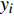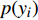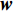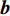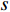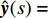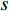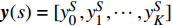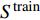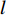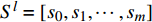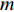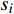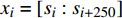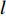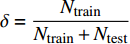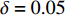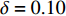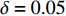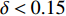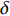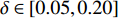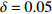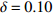Bearing Fault Diagnosis Based on DRSN-CW and LSTM
-
摘要: 利用深度残差网络中逐通道不同阈值的残差收缩模块(DRSN-CW)的降噪能力和特征提取能力,结合长短时记忆网络(LSTM)和注意力机制,设计了一个端到端的基于振动信号的轴承故障诊断模型DRSNCW-LSTM。其中,LSTM模块很好地利用了信号的时序特点,充分提取振动信号的内部时域特征。同时,注意力机制的引入可以使得模型自动提取出重要的时域特征用于后续的故障类型识别。在凯斯西储大学(CWRU)数据集上对提出的模型进行了测试,实验表明提出的方法在无降噪处理的情况下,相比于最新的MCNN-LSTM模型能更准确地诊断轴承故障。在训练数据不足的情况下,提出的方法依旧能较好地实现轴承故障诊断,平均准确率能达到98.16%,比MCNN-LSTM平均提升了2.62%。Abstract: In this paper, based on the noise reduction capability and feature extraction capability of deep residual shrinkage networks with channel-wise thresholds (DRSNCW) module, combined with long short-term memory network (LSTM) and attention mechanism module, an end-to-end vibration signal-based bearing fault diagnosis model, named DRSNCW-LSTM, is proposed. In this model, LSTM module makes good use of the time-series characteristics of the signal to sufficiently extract the internal time-domain features of the vibration signal. Moreover, the introduction of attention mechanism enables the model to automatically extract important time-domain features for follow-up fault type recognition. The effectiveness of the proposed model is validated on the authoritative case Western Reserve University (CWRU) dataset, and experiments show that the proposed method can achieve more accurate bearing fault diagnosis than the state-of-the-art multi-scale convolutional neural network-LSTM (MCNN-LSTM) model without noise reduction processing. In particular, in the case of insufficient training data, the proposed method still achieves rather good bearing fault diagnosis with an average accuracy of 98.16%, which is an average improvement of 2.62% over the MCNN-LSTM.
-
Keywords:
- attention mechanism /
- DRSN-CW /
- fault detection /
- LSTM /
- signal processing
-
滚动轴承是现代机械设备中广泛应用的零部件之一,它依靠主要元件间的滚动接触来支撑机械设备的运行,在飞机、风力涡轮机、铁路轴和发电机等多个行业中应用广泛。这些机器系统在某些不利条件下运行时,一个微小的故障就可能导致一连串的电机损坏,具有维护成本高、经济损失严重和安全隐患重大等问题[1–4]。特别地,在高速、重载、极端工作温度和污染等严酷环境下,机械系统中的轴承很容易发生故障。因此,轴承的故障诊断在系统运行过程中至关重要。
轴承故障诊断的一个重要手段是利用轴承的振动信号进行检测。基于轴承振动信号的故障诊断一般分为两个阶段:特征提取和分类[5]。传统机器学习的特征大致可分为3种不同类型:时域(time-domain)[6]、频域(frequency-domain)[7]和时频域(time-frequency-domain)[8]。由于信号的时域特征较为简单,不能准确表示轴承所有的故障信息。因此,需要将时域信息转化为表达更丰富的频域或时频域信息,如振幅谱[9]、功率谱[10]、傅里叶变换[11]和经验模式分解[12]等。然而,并非所有的特征都对诊断有用,许多特征不仅会增加计算复杂度,而且会降低故障分类的准确性。因此,需要利用特征降维技术,从高维特征中选择合适的特征,只将这些相关的特征输入分类器对信号进行分类。
在传统的轴承故障诊断过程中,信号特征的提取相当耗时,并且强依赖于专业的信号处理知识。随着深度学习的发展,相继提出了基于深度神经网络学习的轴承故障诊断方法。文献[13]在对原始数据进行离散傅里叶变换后,利用卷积神经网络(convolutional neural network, CNN)自动提取用于轴承故障诊断的特征。文献[5,14-17]针对CNN进行改进,尝试在世界公认的轴承故障诊断标准数据[18]−凯斯西储大学(Case Western Reserve University, CWRU)数据集[19]上提升故障诊断效果。为了考虑信号的时序信息,文献[20]结合长短期记忆(long short-term memory, LSTM)模型,提出了一种含有3个LSTM模块的分层深度学习轴承故障诊断算法。之后,文献[21]利用CNN分别提取信号的高频信息和低频信息,提出了MCNN-LSTM模型。特别地,由于ResNet-50[22]在图像领域能提取高质量的图像特征,文献[23]将时域故障信号转换为RGB图像格式作为输入,提出了TCNN(ResNet-50)模型。
然而,轴承振动信号是由放置在设备上的传感器所收集,收集到的信号中往往包含大量噪音。在噪声的干扰下,卷积核学习到的深层特征往往判别性不足,不能准确地进行故障分类。因此,在上述端到端的深度学习故障诊断算法中,诊断前需要进行信号去噪。在传统的信号去噪算法中通常采用软阈值法处理,如小波阈值法,它由3个步骤组成:小波分解、软阈值和小波重构。为了保证信号去噪的性能,小波阈值法的一个关键任务是设计一个滤波器,将噪声信息转换为接近零的特征。然而,设计这样一个滤波器通常很难设置合适的阈值。将软阈值和深度学习相结合是消除噪声、构造高分辨特征的新途径。针对这一问题,文献[24]设计了两种深度残差收缩网络(deep residual shrinkage networks,DRSN):通道共享阈值残差收缩模块(residual shrinkage building unit with channel-shared thresholds, RSBU-CS) 与逐通道不同阈值的残差收缩模块(deep residual shrinkage networks with channel-wise thresholds, DRSN-CW),通过机器学习的方法自适应确定软阈值以消除噪声的影响,软阈值的加入使得两种DRSNs能有效减少数据中噪声的影响,从而提高特征的有效性。RSBU-CS与DRSN-CW的区别在于,特征图的每个通道是否有独立的阈值。RSBU-CS的所有特征通道使用相同的阈值,在特征映射过程中,不同通道通常包含不同数量的噪声。相比于RSBU-CS,DRSN-CW允许特征映射过程中每个信道具有自己的阈值。因此,DRSN-CW比RSBU-CS具有更高的特征提取能力。
基于DRSNs中的DRSN-CW模块,本文设计了一个无需对信号进行前期处理的端到端轴承故障诊断模型DRSN-LSTM,模型分为特征提取和故障分类两个阶段。在特征提取阶段,DRSN-CW模块能有效提取频域中的有用信息,并自动去掉噪声信息,使提取到的特征更有鉴别性。在故障分类阶段,首先利用LSTM提取时域信息,接着引入self-attention机制,在分类任务前自动关注时域信息中的有用信息,最后将时域信息与频域信息融合,再次采用LSTM进行分类。
1. 基于DRSN-CW和LSTM的轴承故障诊断模型
将原始信号数据直接输入神经网络,而无需前期的信号预处理等操作。利用深度学习,自动从原始的含噪声的振动信号数据中提取特征,以用于轴承的故障诊断。
1.1 特征提取阶段
基于本文采取DRSN-CW模型对带噪声的信号进行特征提取和降噪,以获得更具辨识度的信号特征。在特征提取阶段,本文首先利用一个卷积核为20×20,步长为2的一维卷积(Conv1D)对输入信号(或特征)的局部区域进行卷积运算,产生相应的特征。然后利用DRSN-CW对信号噪声的学习能力,在消除原始信号中噪声的同时,提取出更为高级的信号特征。DRSN-CW中同样采用大感受野(
$ 20 \times 20 $ 和$ 10 \times 10 $ )的卷积进行特征提取。最终,将提取的特征输入分类器(堆叠LSTM网络),用于轴承故障的诊断。1.2 轴承信号分类
在轴承信号分类与故障诊断阶段,首先利用LSTM模型抽取振动信号特征之间的时序信息。LSTM是一种时间循环神经网络,解决了常规循环神经网络(recurrent neural network, RNN)存在的长期依赖问题,即当相关信息和当前预测位置之间的间隔变得非常大时,RNN会丧失学习远距离信息的能力。造成长期依赖问题的主要原因在于,RNN在反向传播中很容易出现梯度消失或梯度爆炸的问题,导致长距离的信息丢失。而LSTM通过增加输入门(input gate)、输出门(output gate)和遗忘门(forget gate)解决了这些问题。图1显示了LSTM神经元的内部结构。
沿时间轴,LSTM利用上述3个门控制信息在“细胞”内的传递,更新当前“细胞”状态。输入门决定了输入
$ {{\boldsymbol{x}}_t} $ 和前一层的隐藏状态$ {{\boldsymbol{h}}_{t - 1}} $ 是否应该被添加到当前单元状态。遗忘门与前一个隐藏状态$ {{\boldsymbol{h}}_{t - 1}} $ 和当前输入$ {{\boldsymbol{x}}_t} $ 有关,它决定当前单元值是否保留。最后,输出门利用一个tanh层判断输出哪些状态特征,作为下一个“细胞”的输入。LSTM神经元在每一步都会输出一个状态响应列表,其中包含之前的输出信息和当前的输入信息。记忆单元确保梯度可以传递到许多时间步,而不会出现梯度消失或爆炸的情况。因此,LSTM克服了训练过程中由梯度消失效应造成的困难。3个门的具体计算方法如下:$$ {i_t} = \sigma ({{{{\boldsymbol{W}}}}_i} [{{{{\boldsymbol{h}}}}_{t - 1}},{{{{\boldsymbol{x}}}}_t}] + {{{{\boldsymbol{b}}}}_i}) $$ (1) $$ {f_t} = \sigma ({{{{\boldsymbol{W}}}}_f} [{{{{\boldsymbol{h}}}}_{t - 1}},{{{{\boldsymbol{x}}}}_t}] + {{{{\boldsymbol{b}}}}_f}) $$ (2) $$ {o_t} = \sigma ({{{{\boldsymbol{W}}}}_o} [{{{{\boldsymbol{h}}}}_{t - 1}},{{{{\boldsymbol{x}}}}_t}] + {{{{\boldsymbol{b}}}}_o}) $$ (3) $$ {C_t} = {f_t} \odot {C_{t - 1}} + {i_t} \odot \tanh ({{{{\boldsymbol{W}}}}_C} [{{{{\boldsymbol{h}}}}_{t - 1}},{{{{\boldsymbol{x}}}}_t}] + {{{{\boldsymbol{b}}}}_C}) $$ (4) $$ {h_t} = {o_t} \odot \tanh ({C_t}) $$ (5) 式中,
${{{\boldsymbol{b}}}}$ 表示偏置;${{{\boldsymbol{W}}}}$ 表示网络的权重。在第$ t $ 次更新中,输入门$ {i_t} $ 、遗忘门$ {f_t} $ 、输出门$ {o_t} $ 和单元状态$ {C_t} $ 根据$ t - 1 $ 时刻的隐藏状态$ {{\boldsymbol{h}}_{t - 1}} $ 和当前时刻输入$ {{\boldsymbol{x}}_t} $ 进行更新。在抽取出振动信号特征之间的时序信息后,再利用Self-attention机制,挖掘时序信号特征的相对重要性,使得模型更关注重要的时序信息,忽略其他不重要的时序信息。
$ {{{{\boldsymbol{H}}}}^1} \in {\mathbb{R}^{d \times N}} $ 表示第一层LSTM模型各个时刻的输出向量$ [{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_2},\cdots,{{\boldsymbol{h}}_N}] $ 所组成的矩阵,$ N $ 表示第一层LSTM的时间步长。注意力权重为${\boldsymbol{ \alpha}} = {{\rm{softmax}}} ({{{{\boldsymbol{W}}}}_h}{{{{{\boldsymbol{H}}}}}^1})$ ,其中${{{{{\boldsymbol{W}}}}}_h} \in {\mathbb{R}^{d \times d}}$ 为模型参数,注意力权重${\boldsymbol{\alpha}} \in {\mathbb{R}^N}$ 。结合注意力权重,将新的特征向量
${{{{\boldsymbol{H}}}}^2} = {{{{\boldsymbol{H}}}}^1}{{\boldsymbol{ \alpha}}^{\rm{T}}}$ 输入到下一层LSTM中。最后,将尾端输出向量${{{\boldsymbol{x}}}}$ 作为特征进行分类。为避免故障分类造成过拟合,在最后一层LSTM后加入Dropout层,以一定概率将神经单元暂时屏蔽。1.3 模型训练
完整模型网络结构如图2所示。经过softmax分类函数后,模型可以预测该信号
$ s $ 为类别$ {y_i} $ 的概率$ p({y_i}) $ ,具体计算公式为:$$ p({y_i}|s) = \frac{{{{\rm{e}}^{{{{\boldsymbol{w}}}}_i^{\rm{T}}{{{\boldsymbol{x}}}} + {{{{\boldsymbol{b}}}}_i}}}}}{{\displaystyle\sum\limits_{j \in [0,K]} {{{\rm{e}}^{{{{\boldsymbol{w}}}}_j^{\rm{T}}{{{\boldsymbol{x}}}} + {{{{\boldsymbol{b}}}}_j}}}} }} $$ (6) 式中,
${{{\boldsymbol{w}}}}$ 为全连接层权重;${{{\boldsymbol{b}}}}$ 为偏置项;$ K $ 为类别数量。最终得到信号$ s $ 的输出概率向量$\hat {\boldsymbol{y}}(s) = [p({y_0}|s),p({y_1}|s),\cdots,p({y_K}|s)]$ 。若信号$ s $ 的真实one-hot标签向量为${\boldsymbol{y}}(s) = [y_0^S,y_1^S,\cdots,y_K^S]$ ,则最终目标函数定义为:$$ J = \frac{1}{{{N_{{\rm{train}}}} K}}\sum\limits_{s \in {S^{{\rm{train}}}}} {\sum\limits_{j \in [0,K]} {{{\left( {{y_j} - p({y_j}|s)} \right)}^2}} } $$ (7) 式中,
${S^{{\rm{train}}}}$ 为训练样本;${N_{{\rm{train}}}}$ 为训练样本的数目。为了学习到网络最佳超参数,本文采用能自动调整学习率的Adam(adaptive moments)[25]算法优化目标函数,设定初始化学习率为0.006。2. 实验与讨论
2.1 数据集与评估方法
本文的原始实验数据是从CWRU轴承数据中心[19]以12 kHz的采样频率从电机驱动机械系统的加速计中获得。被诊断的轴承一共有3种缺陷类型,分别是滚动体损伤、外圈损伤与内圈损伤,损伤直径的大小分别为0.007 、 0.014和 0.021 inch,共有10种故障类别(包括正常轴承)。针对不同马力(horsepower, HP)负载情况,收集了0、1、2和3 HP负载下10种不同类型的故障。
为了得到轴承故障诊断模型的训练集,针对每类故障
$ l $ 的原始有序信号数据$ {S^l} = [{s_0},{s_1},\cdots,{s_m}] $ ,其中$ m $ 是原始信号长度,随机从前50%的信号序列中选取${N_{{\rm{train}}}}$ 个数据点。为了采样信号样本,本文设置信号样本的长度为250,即对每个数据点$ {s_i} $ ,截取$ {x_i} = [{s_i}:{s_{i + 250}}] $ 作为一条信号样本。最终,${N_{{\rm{train}}}}$ 个长度为250的信号样本组成了模型的训练集。同理,从后50%的数据集中,采用相同的方法得到规模为${N_{{\rm{test}}}}$ 的测试集。本实验中,对每类故障类别的数据采样1000条长度为250的信号(即$N_{{\rm{train}}}^l + N_{{\rm{test}}}^l = 1\;000$ ,其中$ l $ 为故障类别。因此,对10种故障类型,本文共采样10000条信号用于训练和测试。同时,为了方便描述,本文定义训练集比例为$\delta = \dfrac{{{N_{{\rm{train}}}}}}{{{N_{{\rm{train}}}} + {N_{{\rm{test}}}}}}$ 。为了评估模型对轴承故障的诊断能力,本文采用准确度(Accuracy)、精确度(Precision)、召回率(Recall)和F1分数来验证模型的有效性,其计算公式为:
$$ {{\rm{Accuracy}}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{FP}} + {\rm{FN}} + {\rm{TN}}}} $$ (8) $$ {{\rm{Precision}}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}} $$ (9) $$ {{\rm{Recall}}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}} $$ (10) $$ {{\rm{F}}} 1 = \frac{{2 \times {{\rm{Precision}}} \times {{\rm{Recall}}} }}{{{{\rm{Precision}}} + {{\rm{Recall}}} }} $$ (11) 式中,TP、FP、FN和TN分别代表真阳性、假阳性、假阴性和真阴性结果的数量。针对CWRU中的10个故障类型,分别将每种类型都看做正样本,剩下的类型看做负样本。真阳性就代表被模型预测为正的正样本,假阳性代表被模型预测为正的负样本,假阴性代表被模型预测为负的正样本,真阴性代表被模型预测为负的负样本。
2.2 实验及分析
MCNN-LSTM[21]方法已远超于其他传统方法,平均故障检测准确率超过90%,因此本文只选择MCNN-LSTM模型作为对比算法。除此以外,在模型训练之前,MCNN-LSTM采用下采样以达到降噪的目的,而本文模型不进行任何信号预处理。
在CWRU数据集中的0、1、2和3 HP这4类负载数据集上进行实验,设定
$ \delta = 0.05 $ 和0.10进行训练集信号采样,最终实验结果见表1。表1中的Precision、Recall和F1为10类故障的均值。实验表明,在训练集相对充足的情况下($ \delta = 0.10 $ ),本文方法在4项指标上都略优于MCNN-LSTM。而当训练数据进一步减少,$ \delta = 0.05 $ 时,本文方法明显优于MCNN-LSTM。主要原因在于训练数据量较低的情况下,利用DRSN-CW能提取更有鉴别性的特征。同时,DRSN-CW为每个特征通道学习到了独立的降噪阈值,有偏向性的降噪相比于MCNN-LSTM采用的简单下采样降噪方法,能保留更多的信号特征。特别是在训练数据量不足的情况下,DRSN-CW保留的信号特征越多,所得到的特征也就更丰富。另外,引入注意力机制使得时序信息能更好地融入信号特征中,从而得到准确性更高的特征。表 1 轴承故障诊断实验结果$ \delta = 0.05 $ MCNN-LSTM[21] DRSNCW-LSTM DataSet Accuracy Precision Recall F1 Accuracy Precision Recall F1 0 HP 0.92505 0.92686 0.92505 0.92550 0.97842 0.97861 0.97842 0.97838 1 HP 0.95474 0.95540 0.95474 0.95442 0.97305 0.97342 0.97305 0.97284 2 HP 0.98474 0.98561 0.98474 0.98482 0.98737 0.98746 0.98737 0.98739 3 HP 0.95705 0.95813 0.95705 0.95706 0.98747 0.98797 0.98747 0.98746 $\delta = 0.10$ MCNN-LSTM[21] DRSNCW-LSTM DataSet Accuracy Precision Recall F1 Accuracy Precision Recall F1 0 HP 0.97389 0.97409 0.97389 0.97389 0.98967 0.98984 0.98967 0.98964 1 HP 0.98333 0.98346 0.98333 0.98328 0.98989 0.98995 0.98989 0.98986 2 HP 0.99122 0.99138 0.99122 0.99124 0.99511 0.99520 0.99511 0.99512 3 HP 0.98600 0.98614 0.98600 0.98597 0.99356 0.99362 0.99356 0.99357 为了进一步验证训练集对模型分类的影响,取
$ \delta \in [0.05,0.50] $ 进行轴承故障诊断实验,如图4所示。从图3看出,在4类负载的数据集中,提出的DRSNCW-LSTM在$ \delta < 0.15 $ 时,轴承故障诊断准确率明显高于MCNN-LSTM。随着$ \delta $ 的增大,训练集越来越丰富,两者均能很好地诊断出轴承的故障,诊断准确率也都达到了99%以上。而在0 HP与1 HP数据集中,本文方法能更快地达到99%的准确率。为了验证分类模块中加入的Attention机制是否有效,在移除注意力机制后进行了消融实验,结果如图4所示。在训练集有限的情况下
$ \delta \in [0.05,0.20] $ ,引入Attention后的模型明显优于无Attention的模型。随着训练数据量的增加,两个模型都能很好地提取出信号的有效特征,轴承故障诊断准确率均能达到99%以上。注意力机制的引入是为了融合信号的时域与频域信息。在训练样本缺失,特征提取不足的情况下,注意力机制能极大地补充轴承振动信号的特征信息,为后续的故障诊断带来明显增益。3. 结 束 语
本文提出了一种新的端到端的滚动轴承故障智能诊断模型,该模型包括特征提取模块和分类器模块。特征提取模块在对原始数据进行降噪处理的同时,学习到更有鉴别性的频域特征。在分类模块中,由于输入的特征为序列化的频域特征,而LSTM可以很好地利用信号的时序特点,提取频域特征之间的时域特征,同时,注意力机制的引入使得模型能自动提取出重要的时域特征。将时域信息与频域信息融合后,使用softmax函数将神经元输出转换为滚动轴承故障(包括正常)的概率分布。本文在CWRU轴承数据集下验证了所提出的故障诊断模型的可行性,在训练集充足的情况下,本文提出的DRSNCW-LSTM模型略优于当前最新的MCNN-LSTM模型。而当训练集缺乏时,本文模型在4个数据集上平均准确率达到了98.16%,对比MCNN-LSTM模型,准确率平均提升了2.6%。在没有任何信号预处理的专业知识背景下,本文方法能准确地诊断出轴承的故障,提高机械系统的可靠性,可以有效避免大型事故的发生。
-
表 1 轴承故障诊断实验结果
$ \delta = 0.05 $ MCNN-LSTM[21] DRSNCW-LSTM DataSet Accuracy Precision Recall F1 Accuracy Precision Recall F1 0 HP 0.92505 0.92686 0.92505 0.92550 0.97842 0.97861 0.97842 0.97838 1 HP 0.95474 0.95540 0.95474 0.95442 0.97305 0.97342 0.97305 0.97284 2 HP 0.98474 0.98561 0.98474 0.98482 0.98737 0.98746 0.98737 0.98739 3 HP 0.95705 0.95813 0.95705 0.95706 0.98747 0.98797 0.98747 0.98746 $\delta = 0.10$ MCNN-LSTM[21] DRSNCW-LSTM DataSet Accuracy Precision Recall F1 Accuracy Precision Recall F1 0 HP 0.97389 0.97409 0.97389 0.97389 0.98967 0.98984 0.98967 0.98964 1 HP 0.98333 0.98346 0.98333 0.98328 0.98989 0.98995 0.98989 0.98986 2 HP 0.99122 0.99138 0.99122 0.99124 0.99511 0.99520 0.99511 0.99512 3 HP 0.98600 0.98614 0.98600 0.98597 0.99356 0.99362 0.99356 0.99357 -
[1] ZHANG P, DU Y, HABETLER T G, et al. A survey of condition monitoring and protection methods for medium-voltage induction motors[J]. IEEE Transactions on Industry Applications, 2011, 47(1): 34-46. DOI: 10.1109/TIA.2010.2090839
[2] ZHANG S, ZHANG S B, WANG B N, et al. Deep learning algorithms for bearing fault diagnostics-a comprehensive review[J]. IEEE Access, 2020, 8: 29857-29881. DOI: 10.1109/ACCESS.2020.2972859
[3] BENBOUZID M E H. A review of induction motors signature analysis as a medium for faults detection[J]. IEEE Transactions on Industrial Electronics, 2000, 47(5): 984-993. DOI: 10.1109/41.873206
[4] BENBOUZID M E H, VIEIRA M, THEYS C. Induction motors' faults detection and localization using stator current advanced signal processing techniques[J]. IEEE Transactions on Power Electronics, 1999, 14(1): 14-22. DOI: 10.1109/63.737588
[5] TIAN Y L, LIU X Y. A deep adaptive learning method for rolling bearing fault diagnosis using immunity[J]. Tsinghua Science and Technology, 2019, 24(6): 750-762. DOI: 10.26599/TST.2018.9010144
[6] ZHOU W, HABETLER T G, HARLEY R G. Bearing fault detection via stator current noise cancellation and statistical control[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4260-4269. DOI: 10.1109/TIE.2008.2005018
[7] SCHOEN R R, HABETLER T G, KAMRAN F, et al. Motor bearing damage detection using stator current monitoring[J]. IEEE Transactions on Industry Applications, 1995, 31(6): 1274-1279. DOI: 10.1109/28.475697
[8] EREN L, DEVANEY M J. Bearing damage detection via wavelet packet decomposition of the stator current[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(2): 431-436. DOI: 10.1109/TIM.2004.823323
[9] WIDODO A, YANG B S. Application of nonlinear feature extraction and support vector machines for fault diagnosis of induction motors[J]. Expert Systems with Applications, 2007, 33(1): 241-250. DOI: 10.1016/j.eswa.2006.04.020
[10] PETSOUNIS K A, FASSOIS S D. Parametric time-domain methods for the identification of vibrating structures-a critical comparison and assessment[J]. Mechanical Systems and Signal Processing, 2001, 15(6): 1031-1060. DOI: 10.1006/mssp.2001.1424
[11] WU C X, CHEN T F, JIANG R, et al. A novel approach to wavelet selection and tree kernel construction for diagnosis of rolling element bearing fault[J]. Journal of Intelligent Manufacturing, 2017, 28(8): 1847-1858.
[12] JANTUNEN E, VAAJOENSUU E. Self adaptive diagnosis of tool wear with a microcontroller[J]. Journal of Intelligent Manufacturing, 2010, 21(2): 223-230. DOI: 10.1007/s10845-008-0195-0
[13] JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound and Vibration, 2016, 377: 331-345. DOI: 10.1016/j.jsv.2016.05.027
[14] WEN L, LI X Y, GAO L, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998. DOI: 10.1109/TIE.2017.2774777
[15] ZHUANG Z L, QIN W. Intelligent fault diagnosis of rolling bearing using one-dimensional multi-scale deep convolutional neural network based health state classification[C]//2018 IEEE 15th International Conference on Networking, Sensing and Control (ICNSC). [S.l.]: IEEE, 2018: 1-6.
[16] GUO S, YANG T, GAO W, et al. An intelligent fault diagnosis method for bearings with variable rotating speed based on pythagorean spatial pyramid pooling CNN[J]. Sensors, 2018, 18(11): E3857. DOI: 10.3390/s18113857
[17] 陈保家, 陈学力, 沈保明, 等. CNNLSTM深度神经网络在滚动轴承故障诊断中的应用[J]. 西安交通大学学报, 2021, 55(6): 28-36. DOI: 10.7652/xjtuxb202106004 CHEN B J, CHEN X L, SHEN B M, et al. An application of convolution neural network and long short-term memory in rolling bearing fault diagnosis[J]. Journal of Xi'an Jiaotong University, 2021, 55(6): 28-36. DOI: 10.7652/xjtuxb202106004
[18] NEUPANE D, SEOK J. Bearing fault detection and diagnosis using case Western Reserve University dataset with deep learning approaches: A review[J]. IEEE Access, 2020, 8: 93155-93178. DOI: 10.1109/ACCESS.2020.2990528
[19] SMITH W A, RANDALL R B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study[J]. Mechanical Systems and Signal Processing, 2015, 64: 100-131.
[20] YU L, QU J L, GAO F, et al. A novel hierarchical algorithm for bearing fault diagnosis based on stacked LSTM[J]. Shock & Vibration, 2019, 2019: 2756284.1-2756284.10.
[21] CHEN X H, ZHANG B K, GAO D. Bearing fault diagnosis base on multi-scale CNN and LSTM model[J]. Journal of Intelligent Manufacturing, 2021, 32: 971-987. DOI: 10.1007/s10845-020-01600-2
[22] HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2016: 770-778.
[23] WEN L, LI X Y, GAO L. A transfer convolutional neural network for fault diagnosis based on ResNet-50[J]. Neural Computing & Applications, 2020,
[24] ZHAO M H, ZHONG S S, FU X Y, et al. Deep residual shrinkage networks for fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2020, 99: 1.
[25] KINGMA D, BA J. Adam: A method for stochastic optimization[EB/OL]. [2021-06-12]. https://arxiv.org/pdf/1412.6980.pdf.
-
期刊类型引用(4)
1. 张雄,李嘉禄,董帆,武文博,万书亭,顾晓辉. 箱型图与特征融合模型在轮对轴承标签混淆数据分类中的应用. 振动工程学报. 2025(01): 88-95 .  百度学术
百度学术
2. 王小聪,郝正航,陈卓. 基于DRSN-CW-LSTM网络的锂电池荷电状态预测. 南方电网技术. 2024(02): 106-114 .  百度学术
百度学术
3. 杨金龙,董绍江,牟小燕. 基于随机LSTM块映射特征提取的旋转机械故障诊断方法. 陕西科技大学学报. 2024(04): 142-153 .  百度学术
百度学术
4. 吴胜利,周燚,邢文婷. 基于SDP和MCNN-LSTM的齿轮箱故障诊断方法. 振动与冲击. 2024(15): 126-132+178 .  百度学术
百度学术
其他类型引用(15)

 ISSN
ISSN 



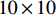

 下载:
下载: