2. 平顶山学院计算机科学与技术学院 河南 平顶山 467002;
3. 西安电子科技大学综合业务网国家重点实验室 西安 710071;
4. 河南宇通信息技术有限公司 郑州 450003
2. College of Computer Science and Technology, Pingdingshan University Pingdingshan Henan 467002;
3. State Key Laboratory of Integrated Service Networks, Xidian University Xi'an 710071;
4. Henan Yu-tong Information Technology Co., Ltd. Zhengzhou 450003
信息置乱变换既可作为信息加密的一种方法,又可作为进一步隐藏的预处理过程,越来越多地受到众多学者的关注。具有混沌特性的Arnold变换[1-3]用于图像置乱能取得很好的效果[4],因而受到学术界的重视,而Arnold变换与Fibonacci数列有关[2]。显然确定变换矩阵的周期是其用于图像置乱变换的重要基础[5],近十年来世界范围内的学者从不同的数学角度寻找计算周期的算法[3, 5-11],但鲜有这方面的理论分析结果。文献[2]研究了矩阵变换(模运算)具有周期的充要条件;文献[11]发现了二维Arnold变换的周期性与Fibonacci模数列周期性的内在联系,开辟了通过求模数列的周期来确定矩阵变换周期的新方法。基于该思路,本文研究三维Arnold变换的模周期性与孪生Fibonacci数列对[12-13]的模周期的关系。
1 基础知识下面介绍有关孪生Fibonacci数列对及其性质定理[12-13],以及相关的矩阵知识。
定义 1 孪生Fibonacci数列对{FFn}定义如下:
| $ \left\{ \begin{array}{l} F{A_0} = 1,F{A_1} = 1,F{A_{n + 1}} = F{A_n} + F{A_{n - 1}} + F{B_n}\\ F{B_0} = 0,F{B_1} = 1,F{B_{n + 1}} = F{A_n} + F{B_n} \end{array} \right. $ | (1) |
分别记这两个数列为{FAn}和{FBn}。因为{FAn}、{FBn}类似Fibonacci数列,所以将这两个数列一起定义为孪生Fibonacci数列对。
引理 1 孪生Fibonacci数列对中{FAn}、{FBn}的模数列{FAn(mod m)}={an}、{FBn(mod m)}={bn}都是周期数列且周期相同。
定义 2 孪生Fibonacci数列对中{FFn}的模数列分别是{FAn(mod m)}={an}、{FBn(mod m)}={bn},其最小正周期T定义为min{T:an+T=an, bn+T=bn, n=0, 1, 2, 3, …},简记为ordm(FFn)。
引理 2 设p为素数,r>1的正整数,若孪生Fibonacci数列对{FFn}的模数列{an(p)}, {bn(p)}的最小正周期为T,则模数列{an(pr)}, {bn(pr)}的最小正周期为pr-1T。
引理 3 N为正整数,且N的因式分解为N=p1r1, p2r2, …, pmrm,其中pi和pj(i≠j)是互不相同的素数,ri≥1(1≤i≤m),孪生Fibonacci数列对{FFn}的模数列{an(pi)}, {bn(pi)}的最小正周期为Ti,那么模数列{an(p1r1, p2r2, …, pmrm)}, {bn(p1r1, p2r2, …, pmrm)}的最小正周期为lcm(piri-1Ti, i=1, 2, …, m)。
由引理3可以知道,只要确定孪生Fibonacci数列对{FFn}的模数列{an(pr)}, {bn(pr)}的最小正周期,即可求出模为合数的孪生Fibonacci数列对的模数列的最小正周期。而由引理2可以得知,只要确定孪生Fibonacci数列对{FFn}的模数列{an(p)}, {bn(p)}的最小正周期,即可求出模为素数幂的模数列{an(pr)}, {bn(pr)}的最小正周期。所以研究模为素数的模数列的最小正周期是关键所在。
引理 4[2] 对给定的N阶数字图像p,有变换X'≡AX(mod N),其中A是变换的矩阵,向量X的每一分量的值xi∈{0, 1, 2, …, N-1}。矩阵变换A对所有向量都具有周期的充分必要条件是|A|与N互素。
定义 3[14] 实数R上的n维矩阵构成的集合记为Mn(R),Mn(R)上的可逆元的全体记为GLn(R),当R=ZN时简记为GLn(ZN)。
2 三维Arnold映射的模周期与孪生Fibonacci数列对的模周期的关系 2.1 FF_Q矩阵的周期性定理记变换矩阵FF_Q为:
| $ \mathit{\boldsymbol{Q}} = \left( {\begin{array}{*{20}{c}} 1&1&1\\ 1&1&0\\ {\rm{1}}&{\rm{0}}&{\rm{0}} \end{array}} \right) $ | (2) |
定理 1 设为m≥1的整数,如果孪生Fibonacci数列对{FFn}的模数列{an(m)}, {bn(m)}的最小正周期为T,则FF_Q变换具有周期性且最小正周期等于T。
证明 由孪生Fibonacci数列对{FFn}的定义可以得出:
| $ {\mathit{\boldsymbol{Q}}^n} = \left( {\begin{array}{*{20}{c}} {F{A_n}}&{F{B_n}}&{F{A_{n - 1}}}\\ {F{B_n}}&{F{A_{n - 1}} + F{A_{n - 2}}}&{F{B_{n - 1}}}\\ {F{A_{n - 1}}}&{F{B_{n - 1}}}&{F{A_{n - 2}}} \end{array}} \right)\;\;\;\;\;\;n > 1 $ | (3) |
显然|Qn|=(-1)n,根据引理4可以推出FF_Q变换具有周期性。为叙述方便,记Qn(mod N)为Qn(N)。
根据引理1及性质有下式成立:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}^{n + T}} = \left( {\begin{array}{*{20}{c}} {F{A_{n + T}}}&{F{B_{n + T}}}&{F{A_{n - 1 + T}}}\\ {F{B_{n + T}}}&{F{A_{n - 1 + T}} + F{A_{n - 2 + T}}}&{F{B_{n - 1 + T}}}\\ {F{A_{n - 1 + T}}}&{F{B_{n - 1 + T}}}&{F{A_{n - 2 + T}}} \end{array}} \right) \equiv }\\ {\left( {\begin{array}{*{20}{c}} {{a_{n + T}}}&{{b_{n + T}}}&{{a_{n - 1 + T}}}\\ {{b_{n + T}}}&{{a_{n - 1 + T}} + {a_{n - 2 + T}}}&{{b_{n - 1 + T}}}\\ {{a_{n - 1 + T}}}&{{b_{n - 1 + T}}}&{{a_{n - 2 + T}}} \end{array}} \right) \equiv }\\ {\left( {\begin{array}{*{20}{c}} {{a_n}}&{{b_n}}&{{a_{n - 1}}}\\ {{b_n}}&{{a_{n - 1}} + {a_{n - 2}}}&{{b_{n - 1}}}\\ {{a_{n - 1}}}&{{b_{n - 1}}}&{{a_{n - 2}}} \end{array}} \right) \equiv }\\ {\left( {\begin{array}{*{20}{c}} {F{A_n}}&{F{B_n}}&{F{A_{n - 1}}}\\ {F{B_n}}&{F{A_{n - 1}} + F{A_{n - 2}}}&{F{B_{n - 1}}}\\ {F{A_{n - 1}}}&{F{B_{n - 1}}}&{F{A_{n - 2}}} \end{array}} \right) = {\mathit{\boldsymbol{Q}}^n}({\rm{mod}}\;m)} \end{array} $ | (4) |
这样就证明了孪生Fibonacci数列对{FFn}的模数列{an(m)}, {bn(m)}的最小正周期T也是Q的周期。可以验证:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}^T} = \left( {\begin{array}{*{20}{c}} {F{A_T}}&{F{B_T}}&{F{A_{T - 1}}}\\ {F{B_T}}&{F{A_{T - 1}} + F{A_{T - 2}}}&{F{B_{T - 1}}}\\ {F{A_{T - 1}}}&{F{B_{T - 1}}}&{F{A_{T - 2}}} \end{array}} \right) \equiv }\\ {\left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right) = E({\rm{mod}}\;N)} \end{array} $ | (5) |
下面通过构造一个{FFn}到{Qn}的一一映射来证明T也是Qn的最小正周期。
由孪生Fibonacci数列对{FFn}中的任一对FAi, FBi(i∈Z, i>1),都可以构造一个3×3的矩阵:
| $ \left( {\begin{array}{*{20}{c}} {F{A_i}}&{F{B_i}}&{F{A_{i - 1}}}\\ {F{B_i}}&{F{A_{i - 1}} + F{A_{i - 2}}}&{F{B_{i - 1}}}\\ {F{A_{i - 1}}}&{F{B_{i - 1}}}&{F{A_{i - 2}}} \end{array}} \right) $ |
令f(FAn, FBn)=Qn,便定义了一个映射
| $ \begin{array}{c} f(F{A_i}, F{B_i}) * f(F{A_j}, F{B_j}) = ({\mathit{\boldsymbol{Q}}^i}) * ({\mathit{\boldsymbol{Q}}^j}) = \\ ({\mathit{\boldsymbol{Q}}^{i - 1}} * \mathit{\boldsymbol{Q}}) * ({\mathit{\boldsymbol{Q}}^j}) = ({\mathit{\boldsymbol{Q}}^{i - 1}}) * (\mathit{\boldsymbol{Q}} * {\mathit{\boldsymbol{Q}}^j}) = \\ ({\mathit{\boldsymbol{Q}}^{i - 1}}) * ({\mathit{\boldsymbol{Q}}^{j + 1}}) = {\mathit{\boldsymbol{Q}}^{i + j}} = \\ f(F{A_{i + j}}, F{B_{i + j}}) \end{array} $ | (6) |
式中,*为矩阵乘运算。这样f就是{FFn}到{Qn}的一个同态映射。不难证明f也是一个同构映射。
T是孪生Fibonacci数列对{FFn}的模数列{an(m)}, {bn(m)}的最小正周期,因为f是{FFn}到{Qn}的同构映射,所以T也是FF_Q变换的最小正周期。把Q的最小正周期(多数文献称它为阶)简记为ordN(Q(mod N))或ordN(Q)。
由引理2、引理3和定理1可以得到如下定理:
定理 2 设p为素数,r>1的正整数,且N=pr,则ordN(Q(mod N))=pr-1ordp(Q(mod p))。
定理 3 设为N≥1的整数,且N=uv,u和v互素,则有:
| $ \begin{array}{c} \mathit{\boldsymbol{ }}{\rm{or}}{{\rm{d}}_N}(\mathit{\boldsymbol{Q}}({\rm{mod}}\;N)) = \\ {\rm{lcm}}({\rm{or}}{{\rm{d}}_u}(\mathit{\boldsymbol{Q}}({\rm{mod}}\;u)){\rm{, or}}{{\rm{d}}_v}(\mathit{\boldsymbol{Q}}({\rm{mod}}\;v))) \end{array} $ |
定理 4 设为N≥1的整数,且N的因式分解为N=p1r1, p2r2, …, pmrm,其中pi和pj(i≠j)是互不相同的素数,ri≥1(m≥i≥1),那么有ordN(Q(mod N))=lcm(ordpiri(Q(mod piri)),i=1, 3, …, m。
所以只要确定了模为素数幂的矩阵的阶,即可求出模为合数的阶。
2.2 三维Arnold变换的周期性与FF_Q矩阵的周期性的关系定义 4[2] 对于给定的自然数N≥2,下列变换称为三维Arnold变换:
| $ \left( {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {z'} \end{array}} \right) \equiv \left( {\begin{array}{*{20}{c}} 1&1&1\\ 1&2&2\\ {\rm{1}}&{\rm{2}}&{\rm{3}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right)({\rm{mod}}\;N) $ | (8) |
式中,x, y, z∈{0, 1, 2, …, N-1},而N是数字图像矩阵的阶数。令
引理 5 如果变换
| $ \left( {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {z'} \end{array}} \right) \equiv \left( {\begin{array}{*{20}{c}} 1&1&1\\ 1&2&2\\ {\rm{1}}&{\rm{2}}&{\rm{3}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right)({\rm{mod}}\;N) $ | (9) |
周期为ordN(A(mod N)),则下列变换有周期,且ordN(A'(mod N))=ordN(A(mod N)):
| $ \left( {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {z'} \end{array}} \right) \equiv \left( {\begin{array}{*{20}{c}} 3&2&1\\ 2&2&1\\ {\rm{1}}&{\rm{1}}&{\rm{1}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right) \equiv \mathit{\boldsymbol{A'}}\left( {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right)({\rm{mod}}\;N) $ | (10) |
其中,x, y, z∈{0, 1, 2, …, N-1}。因为x, y, z位置的任意性和变换的线性,引理的证明比较简单,这里省略其证明过程。
引理 6 对于FF_Q的变换矩阵Q,有Q(mod N)∈GLn(ZN)。
1) 由Q生成的群<Q>={Qn(mod N):n∈Z}是GLn(ZN)上的一个交换群。
2) 由Qi(i∈Z)生成的子群<Qi>的阶整除<Q>的阶。
证明 ①对于<Q>中的任意两个元素都可以表示为Qi, Qj(i, j∈Z),由群的指数定理[14]可以得到
②<Qi>是<Q>的子群,由群的拉格朗日定理[14]得到ordN(Qi(mod N))=ordN(Q(mod N))。证毕。
由引理5和引理6立即得到:
定理 5 对于给定的整数N>2,如果三维Arnold变换的周期为ordN(A(mod N)),则FF_Q变换的周期为2ordN(A(mod N)),即ordN(A(mod N))=ordN(FFn)/2。
从上述定理得出:三维Arnold映射的模周期是孪生Fibonacci数列的模周期的一半。例如,ord2(FFn)=7,由引理2得ord64(FFn)=26-1×7=224,由定理1得到ord64(Q(mod 64))=ord64(FFn)=224,由定理5得到三维Arnold变换的周期为112,这个结论与文献[2]的结果是一致的。
综上所述,只要知道孪生Fibonacci数列对{FFn}的模数列{an(m)}, {bn(m)}的周期,便可以确定三维Arnold变换的周期,从而更好地研究图像置乱技术。
3 三维Arnold映射在图像加密中的应用及周期验证 3.1 一个简单图像位置置乱加密算法及周期验证通过分析,可知三维Arnold变换模64的周期为112,但用直观的图示方法验证其正确性却较困难,因此,设计了一种新的图像置乱加密算法,用该算法检验三维Arnold映射的周期的正确性。
1) 图像位置置乱加密算法
① 将s×s的二维平面图像变换成t×t×t的三维立体图像。
② 使用三维Arnold变换对图像像素的位置进行多次映射变换;由于三维Arnold变换在进行图像置乱中对于(0, 0, 0)位置上的像素不起任何作用,因此,可把(0, 0, 0)位置上的像素和一个固定位置(i, j, k)(0<i≤t, 0<j≤t, 0<k≤t)的像素在每轮迭代过程后进行交换。这样,前一轮(0, 0, 0)位置的像素就可以在下一轮迭代中被置乱。其中(i, j, k)也可以被看作密钥进行控制;
③ 将t×t×t的三维立体图像变换成s×s的二维加密图像。
2) 仿真实验
下面给出一个基于Arnold映射的图像仿真变换实例。如图 1a所示,图像像素为512×512,变换成64×64×64的三维立体图。使用三维Arnold映射变换对原始图像作多次变换得到的图像变换状态(image transform state,ITS),可以看出原始图像经过112次变换后恢复到原来状态,从而验证了上述相关定理的正确性。仅就位置置乱而言,效果比二维Arnold映射置乱效果好。本仿真实验在Matlab 2010软件环境下进行。
 |
| 图1 原图像进行n次Arnold变换的效果图 |
1) 图像置乱加密算法
图 1的图像加密算法中将s×s的二维平面图像变换成t×t×t的三维立体图像有时不能成立,如不能将500×500的二维平面图像变换成t×t×t的三维立体图像。下面对3.1节的算法进行改进,增加最少的冗余信息,使得将s×s的二维平面图像变换成t×t×t的三维立体图像。图像位置置乱加密算法由以下5步完成。
① 对给定的s×s求出t的值:
② 将二维图像变换为一维数组,增加t×t×t-s×s个冗余信息,将一维数组变换成t×t×t的三维立体图像。
③ 使用三维Arnold变换对图像像素的位置进行T次映射变换;由于三维Arnold变换在进行图像置乱中对于(0, 0, 0)位置上的像素不起任何作用,因此,可把(0, 0, 0)位置上的像素和一个固定位置(i, j, k)(0<i≤t, 0<j≤t, 0<k≤t)的像素在每轮迭代过程后进行交换。这样,前一轮(0, 0, 0)位置的像素就可以在下一轮迭代中被置乱。其中(i, j, k)也可以被看作密钥进行控制。
④ 求加密后的二维矩阵的阶n:
⑤ 将三维变换为一维数组,增加n×n-t×t×t个冗余信息,将一维数组变换成n×n的二维加密图像用于保存或进一步处理。
2) 仿真实验
如图 2a所示,原始图像像素为440×440。根据算法可以求出t=58,n=442,三维Arnold的周期为14。使用三维Arnold映射变换对原始图像作多次变换得到的图像变换状态如图 2所示,效果比二维Arnold映射置乱效果好。
 |
| 图2 原图像进行n次Arnold变换的效果图 |
在工程实际应用中,s的值一般比较大,如有的卫星图片大小为2 340×3 240,像3.1节一样使用变换矩阵的周期对图像恢复,代价高昂。文献[15-16]详细探讨了Arnold逆变换和使用方法,本文也使用基于Arnold逆变换的方法对图像解密。
基于图像位置置乱的解密算法如下:
1) 对给定的s×s求出t和n的值,方法同加密;
2) 将二维图像变换为一维数组,去冗余信息,将一维数组变换成t×t×t的三维立体图像;
3) 使用三维Arnold变换对图像像素进行T次逆变换;
4) 将三维立体图像变为一维数组,去冗余信息,将一维数组变换成二维图像。
3.2.3 图像位置置乱算法的冗余度在算法中增加了冗余信息,冗余度的大小也是衡量这个算法好坏的一个标准。如当原始图像像素分别440×440,300×300,512×512时,它们的冗余度分别为0.91%,1.34%,0。图 3给出了图像像素在200~2 000之间的冗余度的值,从图上可以看出信息冗余度一般不超过9%,这说明该算法是可用的。
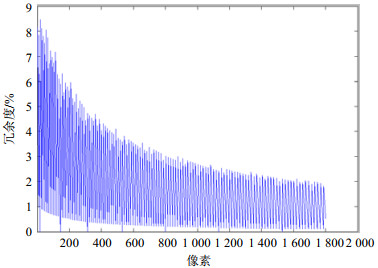 |
| 图3 图像像素在200~2 000之间的冗余度的值 |
与文献[16]相似,为了防止仅作空间置乱有轮廓显现,再引入色彩空间的置乱,然后进行多轮置乱变换。具体步骤是:1)首先使用三维Arnold变换对图像像素坐标进行置乱;2)再使用文献[16]构造的m维广义Arnold变换对图像像素灰度值进行APS变换;3)为了加强安全,重复步骤1)和步骤2)进行多轮乘积型置乱变换,达到高维矩阵置乱的效果。
图 4给出了图像Lena(图 4a,512×512)像素灰度值和坐标双置乱效果图及其相应的直方图。图 4a和图 4b分别为第1轮置乱变换的效果图及其直方图,图 4c和图 4d分别为第18轮置乱变换的效果图及其直方图,图 4e和图 4f分别为解密效果及其直方图。
 |
| 图4 图像双置乱效果图及其相应的直方图 |
通过研究孪生Fibonacci数列对的模数列的性质和定理,研究了FF_Q变换的模周期性,从而获得了三维Arnold变换矩阵的周期性规律,为其在图像置乱编码的应用提供必要的数学理论基础。这种研究方法也对变换矩阵的阶的理论分析开辟了新的途径,也为探讨任意n维Arnold变换矩阵的周期性问题提供了新的方法。下一步的相关工作有4个方面。
1) 秘密图像置乱的效果越好,将其隐藏在公开图像中其安全性越高,针对具有混沌特性的三维Arnold变换用于图像置乱,其置乱程度的进一步研究可以参考文献[2, 17]。
2) 关于三维Arnold映射的周期性与文献[12-13]中孪生Fibonacci数列对的周期性相同。
3) 使用三维Arnold变换对图像像素坐标进行置乱,因其周期性,在安全性(保密性)方面达不到要求,通常情况下一定要和别的加密算法配合使用,如本文中的多轮双置乱加密算法。本文图像加密算法的性能分析,将另文论述。
4) 将继续研究基于三维Arnold映射的多轮双置乱彩色图像加密算法。
| [1] |
ARNOLD V I, AVEZ A. Ergodic problems of classical mechanics[M]// Mathematical Physics Monograph Series NewYork: W A Benjamin, INC, 1968.
|
| [2] |
QI D X, ZOU J CH, HAN X Y. A new class of scrambling transformation and its application in the image information covering[J].
Science in China(Series E), 2000, 43(3): 304–412.
|
| [3] |
DYSON F J. FALK H. Period of a discrete cat map-ping[J]. The American Mathematical Monthly, 1992, 99(7): 603-614.
|
| [4] |
YANG Ya-li, CAI Na, NI Guo-qiang. Digital image scrambling technology based on the symmetry of Arnold transform[J].
Journal of Beijing Institute of Technology, 2006, 15(2): 216–220.
|
| [5] |
杨礼珍, 陈克非. 变换矩阵(mod n)的阶及两种推广Arnold变换矩阵[J].
中国科学, E辑, 2004, 34(2): 151–161.
YANG Li-zhen, CHEN Ke-fei. Rank of transformation matrix(mod I) and two generalized Arnold transformation matrices[J]. Science in China(Series E), 2004, 34(2): 151–161. |
| [6] |
QI D X, WANG D SH, YANG D L. Matrix transformation of digital image and its periodicity[J].
Progress in Natural Science, 2001, 11(7): 542–549.
|
| [7] |
邹建成, 铁小匀. 数字图像的二维Arnold变换及其周期性[J].
北方工业大学学报, 2000, 12(1): 1014–1032.
ZOU Jian-cheng, TIE Xiao-yun. Arnold transformation of digital image with two dimensions and its periodicity[J]. Journal of North China University of Technology, 2000, 12(1): 1014–1032. |
| [8] |
李兵, 徐家伟. Arnold变换的周期及其应用[J].
中山大学学报(自然科学版), 2004, 43(S2): 139–142.
LI Bing, XU Jia-wei. On the periods of Arnold transformations and some applications[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni(Natural Science), 2004, 43(S2): 139–142. |
| [9] |
黎罗罗. Arnold型置乱变换周期分析[J].
中山大学学报(自然科学版), 2005, 44(2): 1–4.
LI Luo-luo. On periods of Arnold _type transformations[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni (Natural Science), 2005, 44(2): 1–4. |
| [10] |
李用江, 李昌利, 葛建华, 等. n维Arnold变换矩阵模pr的周期性研究[J].
数学的实践与认识, 2010, 40(16): 53–59.
LI Yong-jiang, LI Chang-li, GE Jian-hua, et al. Study on the periodicity of n-Arnold-type transformation matrix Mod pr[J]. Mathematics in Practice and Theory, 2010, 40(16): 53–59. |
| [11] |
李用江, 张辰光, 李昌利, 等. 猫映射的周期性与Fibonacci模数列的周期性的内在联系[J].
计算机应用, 2010, 30(4): 38–43.
LI Yong-jiang, ZHANG Chen-guang, LI Chang-li, et al. Inherent relationship between the periodicity of cat map and that of series generated from Fibonacci series[J]. Journal of Computer Applications, 2010, 30(4): 38–43. |
| [12] |
LI Yong-jiang, GE Jian-hua, SUN Zhi-lin, et al. Periods of a new sequence modulo p[J].
Communications in Computer and Information Science, 2011(158): 187–193.
|
| [13] |
LI Yong-jiang, GE Jian-hua, SUN Zhi-lin. Periods of twin Fibonacci sequence modulo pr[J].
Advanced Science Letters, 2012, 7(3): 340–344.
|
| [14] |
GARRETT P. 密码学导论[M]. 吴世忠, 宋晓龙, 郭涛, 译. 北京: 机械工业出版社. 2003.
GARRETT P. An Introduction to cryptology[M]. Translated by WU Shi-zhong SONG Xiao-long, GUO Tao. Beijing: China Machine Press, 2003. |
| [15] |
YANG Ya-li, CAI Na, NI Guo-qiang. Digital image scrambling technology based on the symmetry of Arnold transform[J].
Journal of Beijing Institute of Technology, 2006, 15(2): 216–220.
|
| [16] |
李用江, 葛建华, 李昌利, 等. 一种新的n维广义Arnold矩阵构造方法及其在图像置乱中的应用[J].
北京科技大学学报, 2010, 32(12): 1631–1637.
LI Yong-jiang, GE Jian-hua, LI Chang-li, et al. A new construction method for n-Dimensional generalized Arnold matrix and its application in image scrambling[J]. Journal of University of Science and Technology Beijing, 2010, 32(12): 1631–1637. |
| [17] |
吴旻升, 王介生, 刘慎权. 图像的排列变换[J].
计算机学报, 1998, 21(6): 514–519.
WU Min-sheng, WANG Jie-sheng, LIU Shen-quan. Permutation transform of images[J]. Journal of Computers, 1998, 21(6): 514–519. |
 2015, Vol. 44
2015, Vol. 44
