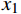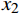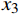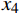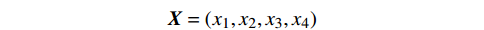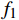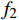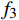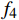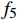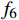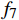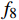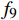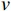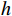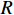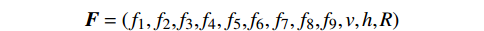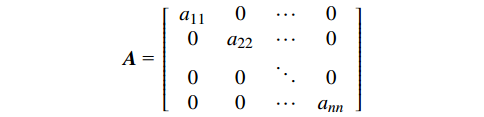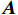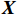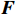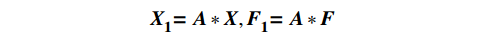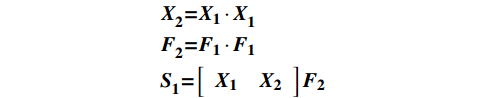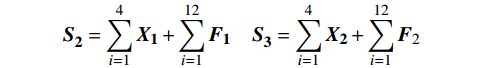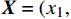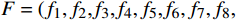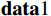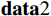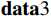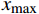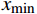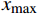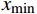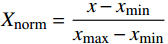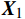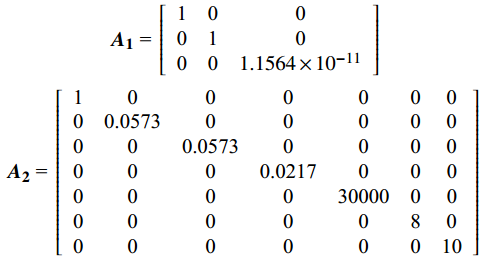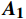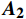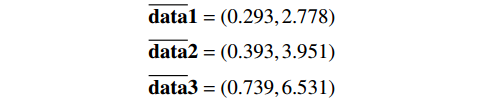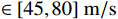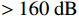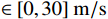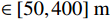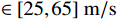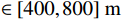Classification and recognition method of small and micro targets in low resolution radar based on high dimensional feature domains
-
摘要:
低空小微目标分类问题是雷达业界的难题之一,严重影响了雷达的探测性能和系统作战指挥效能。为了准确、快速识别旋翼、固定翼等低空小微目标,提出一种基于高维特征域的低分辨雷达小微目标分类识别方法。通过提取信号层的一系列时频微观特征和航迹宏观特征,对特征进行内积、幂变换等获取高维特征域,利用学习树网络建立多层级目标分类识别模型,实现低空小微目标分类标记。研究结果表明,该方法能准确、快速地实现小微目标的分类。
Abstract:The classification of small and micro targets at low altitude is one of the difficult problems in radar field, which seriously effects the detection performance of radar and the effectiveness of system combat command. In order to accurately and quickly identify small and micro targets at low altitude such as rotors, fixed wings and vehicles, a classification and recognition method of small and micro targets of low-resolution radar based on high-dimensional feature domain is proposed in this paper. A series of time-frequency micro features and track macro features are extracted from the signal layer, and high-dimensional feature domain is obtained by internal product and power transformation of features. A multi-level target classification and recognition model is established by using learning tree network to realize the classification and marking of small and micro targets at low altitude. The results show that this method can classify small and micro objects accurately and quickly.
-
低空小微目标的运动特征通常具有飞行高度低、高度区域严重交叉、飞行速度慢且速度范围基本一致、RCS近似等特点。利用速度、高度、幅度等很难将低空小微目标(旋翼无人机、直升机、固定翼等)进行准确的区分,严重影响了雷达的探测性能和系统作战指挥效能。利用单个低分辨雷达设备对低空小微目标的类型进行判别和提示,能大大提高雷达的探测识别能力,同时可对光电、无线电等设备提供准确的引导,提升雷达系统的指控能力。
特征的检测和提取是最终实现目标分类识别的基石,高维特征库可为判别提供准确参照。传统的低分辨雷达检测信息有限,主要包括目标幅度强度、速度、高度等信息,针对低空小微目标分类难的问题,若从单一的特征角度出发,如利用目标速度进行分类,由于旋翼无人机、固定翼无人机等小微目标运行速度范围存在交织,导致分类准确度低;若利用回波幅度强度特性去分析统计目标RCS特性作为参考依据,RCS在一段时间内会随着目标运动、目标视线角和频率的变化而起伏,导致该特征具备一定的局限性。学者们还研究了从低维特征角度出发,提出基于幅度和多普勒频谱的三特征检测,实现目标特征的联合提取,更精细化的挖掘雷达回波特征。
因此,为了进一步提升目标分类识别的准确度,稳健的、高维度的特征组合是必然趋势。联合有限的微观特征和宏观特征,形成多种特征模态,基于高维特征域利用由粗到细的多层级学习网络判别模型,实现对低空小微目标的智能化、精细化描述和识别,实现雷达“看得见(检测能力强)、辨得明(识别概率高)”目标分类能力。
1. 联合特征提取
对包含关注小微目标的雷达回波特征进行分析,提取相位特征、多普勒频谱特征、幅度能量特征等信息,结合小微目标飞行运动特性,提取航迹拟合特征等信息,形成包含微观特征和宏观特征的联合特征库[1-3]。
1.1 信号特征
由于空地运动目标的机械振动或目标上一些旋转部件(如直升机的桨叶、旋翼无人机的旋翼)的转动会对回波信号产生频率调制,表现之一即为雷达目标回波的相位调制,该调制也是微多普勒现象的一种特殊形式,而不同目标的相位调制特征存在差异,这就为目标识别奠定了基础。因此对某型雷达采集的含有关注小微目标的回波信号进行脉冲压缩、MTI、MTD、恒虚警检测(CFAR)处理后,获取目标的检测位置,按照检测位置的距离维信息进行IFFT反馈计算,提取检测目标的信号时频域特征,包括相位特征、多普勒频谱特征、幅度能量特征等[4-6]。
信号特征提取如下。
1)相位系数:
$$ {k_p} = \arctan \left(\sqrt {\frac{M}{{M - 1}}\frac{{1 - {q^{{2}}}}}{{{q^{{2}}}}}} \right) $$ 式中,
$M$ 为单帧积累的脉冲数;$q$ 为$M$ 个脉冲间相位差的和。2)频率波形熵:
${E_x} = - \displaystyle\sum\limits_{i = 1}^n {{p_i}} {\mathrm{ln}}{p_i}$ ,其中${p_i} = {{{y_i}} \Big/ {\displaystyle\sum\limits_{i = 1}^n {{y_i}} }}$ ,$y$ 是雷达波束扫描目标时间内的回波序列的频率数据。3)能量比:
$ Q=\dfrac{去掉多普勒主峰后的剩余能量}{总能量}=\frac{{\displaystyle\sum\limits_{i=1}^{N}|}Z(i){|}^{2}}{{\displaystyle \sum\limits_{i=1}^{N}|}X(i){|}^{2}} $ ,其中,$Z = {\mathrm{fft}}\left( z \right)$ 是去掉多普勒主峰后的频谱。1.2 航迹特征
雷达实测的目标检测点迹均已包含多普勒速度、高度、幅度、信噪比等信息,针对低空目标常规运动特性较为相似的特点,基于航迹宏观特性建模,挖掘更多维度的宏观特征,首先,利用稳定航迹拟合航迹作为真值估计,然后获取航迹的拟合误差均值、方差、航迹点迹的距离的均值、加速度的均值和方差、加加速度的均值和方差等一系列宏观特征。
$$ D={\displaystyle \sum _{i=1}^{n-1} {d}_{i}} \quad{d_i} = \sqrt {{{\left( {{x_{i + 1}} - {x_i}} \right)}^2} + {{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} $$ sn和s1为选择的单元内第一个点迹和最后一个点迹的扫描数,即雷达探测的时间,
$g\left( \cdot \right)$ 为拟合的曲线在$x$ 坐标点的拟合值,一般拟合选择8阶多项式,获得航迹点迹拟合误差:$$ \Delta {y_i} = \left[ {\frac{{{s_n} - {s_1} + 1}}{D}} \right]\left( {{y_i} - g\left( {{x_i}} \right)} \right) $$ 已知目标速度
$v$ ,航迹的加速度和加加速度计算分别为:$ {a}_{i}=\dfrac{{v}_{i+1}-{v}_{i}}{\Delta t},{j}_{i}=\dfrac{{a}_{i+1}-{a}_{i}}{\Delta t}。 $ 通过上述预处理后,挖掘提取以下特征。
1)拟合误差均值
${f_1} = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n \Delta {y_i}$ ;2)拟合误差方差
${f_2} = \dfrac{1}{{n - 1}}\displaystyle\sum\limits_{i = 1}^n {{{\left[ {\Delta {y_i} - {f_1}} \right]}^2}} $ ;3)距离均值
${f_3} = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{r_i}} $ ;4)距离差的最大值
${f_4} = \mathop {\max }\limits_{i \in I} {d_i}$ ,其中$I = \{ 1,2, \cdots , n - 1\} $ ;5)最小值和最大值的比值
${f_5} = \dfrac{{\mathop {\min }\limits_{i \in I} {d_i}}}{{\mathop {\max }\limits_{i \in I} {d_i}}}$ ;6)加速度的均值
${f_6} = \dfrac{1}{{n - 2}}\displaystyle\sum\limits_{i = 1}^{n - 1} {{a_i}} $ ;7)加速度的方差
${f_7} = \dfrac{1}{{n - 2}}\displaystyle\sum\limits_{i = 1}^{n - 1} {{{\left[ {{a_i} - {f_6}} \right]}^2}} $ ;8)加加速度的均值
${f_8} = \dfrac{1}{{n - 2}}\displaystyle\sum\limits_{i = 1}^{n - 1} {{j_i}} $ ;9)加加速度的方差
${f_9} = \dfrac{1}{{n - 2}}\displaystyle\sum\limits_{i = 1}^{n - 1} {{{\left[ {{j_i} - {f_8}} \right]}^2}} $ 。2. 高维特征变换
联合信号微观特征和航迹宏观特征建立特征组合,通过归一化处理,利用特征变换形成高维特征域 [7-9] 。
2.1 线性函数归一化
对特征进行归一化处理,将所有的特征都统一到一个大致相同的数值区间内,使得各个指标量纲统一并具有可比性。首先对原始数据进行线性变换,结果映射到[0,1],实现对原始数据的等比缩放,计算方式如下:
$$ {X_{{\text{norm}}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $$ 式中,
$x$ 为原始数据;$x{}_{\max }$ 为原始数据集的最大值;$x{}_{\min }$ 为原始数据集的最小值。2.2 线性变换
线性变换是属性理论中非常常用的手法,当面对一种难以处理的数学对象时,可以把它转化成另外一种数学对象,同时保持两种数学对象的同构性。线性变换意味着可以将特征空间中的量围绕零点进行旋转伸缩,但不能将其弯曲,否则是非线性变换。线性变换就是一阶导数为常数的函数,如
${\boldsymbol{y}} = k{\boldsymbol{x}}$ ,把${\boldsymbol{y}} = k{\boldsymbol{x}}$ 拓展为$n$ 维空间的映射,$ {\boldsymbol{x}}和{\boldsymbol{y}} $ 看做$n$ 维向量,当$k$ 为常数时,易得满足同质性$f(ka) = kf(a)$ ,当$k$ 为一个矩阵时,易得满足可加性$f(a + b) = f(a) + f(b)$ 。假设一个2维特征$ ({x}_{1},{x}_{2}) $ ,对特征进行不同倍数,如假设为2倍和5倍的拉伸处理,方法就是让特征组合向量都乘以一个对角矩阵:$$ \begin{gathered} \quad\quad\quad\quad\;{\boldsymbol{T}}{\text{ = }}\left| {\begin{array}{*{20}{c}} 2&0 \\ 0&5 \end{array}} \right| \\ {\boldsymbol{T}}\left| {\begin{array}{*{20}{c}} {{x_1}} \\ {x_2^{}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} 2&0 \\ 0&5 \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{x_1}} \\ {x_2^{}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {2{x_1}} \\ {5x_2^{}} \end{array}} \right| \\ \end{gathered} $$ 对特征进行翻转变换处理,就是让该特征组合向量
$ ({x}_{1},{x}_{2}) $ 乘以如下矩阵:$$ {{\boldsymbol{A}}_{\mathbf{1}}} = \left| {\begin{array}{*{20}{c}} 1&0 \\ 0&{-1} \end{array}} \right|,{{\boldsymbol{A}}_{\mathbf{2}}} = \left| {\begin{array}{*{20}{c}} {-1}&0 \\ 0&1 \end{array}} \right| $$ ${{\boldsymbol{A}}_{\boldsymbol{1}}}$ 和${{\boldsymbol{A}}_{\boldsymbol{2}}}$ 矩阵分别可实现该组合特征向量关于${\boldsymbol{K}}$ 轴翻转和${\boldsymbol{Y}}$ 轴翻转。利用矩阵
${\boldsymbol{K}}$ 对特征组合进行剪切变换,实现方法为:$$ \begin{gathered} \quad\quad\quad\quad\quad{\boldsymbol{K}}{\text{ = }}\left| {\begin{array}{*{20}{c}} 1&k \\ 0&1 \end{array}} \right| \\ {\boldsymbol{K}}\left| {\begin{array}{*{20}{c}} {{x_1}} \\ {x_2^{}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} 1&k \\ 0&1 \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{x_1}} \\ {x_2^{}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{x_1} + kx_2^{}} \\ {x_2^{}} \end{array}} \right| \\ \end{gathered} $$ 2.3 非线性变换
非线性是自然界复杂性的典型性质之一,表示变量之间的数学关系,不是直线而是曲线、曲面、或不确定的属性。与线性相比较,非线性更加接近客观事物性质本身。非线性变换的目的就是把原始的特征做非直线的弯曲变换得到一个新的特征,用这个新的特征组合来进行线性分类,对应到原始的空间中,相当于做了非线性分类,利用非线性变换可进一步提升特征的维度。
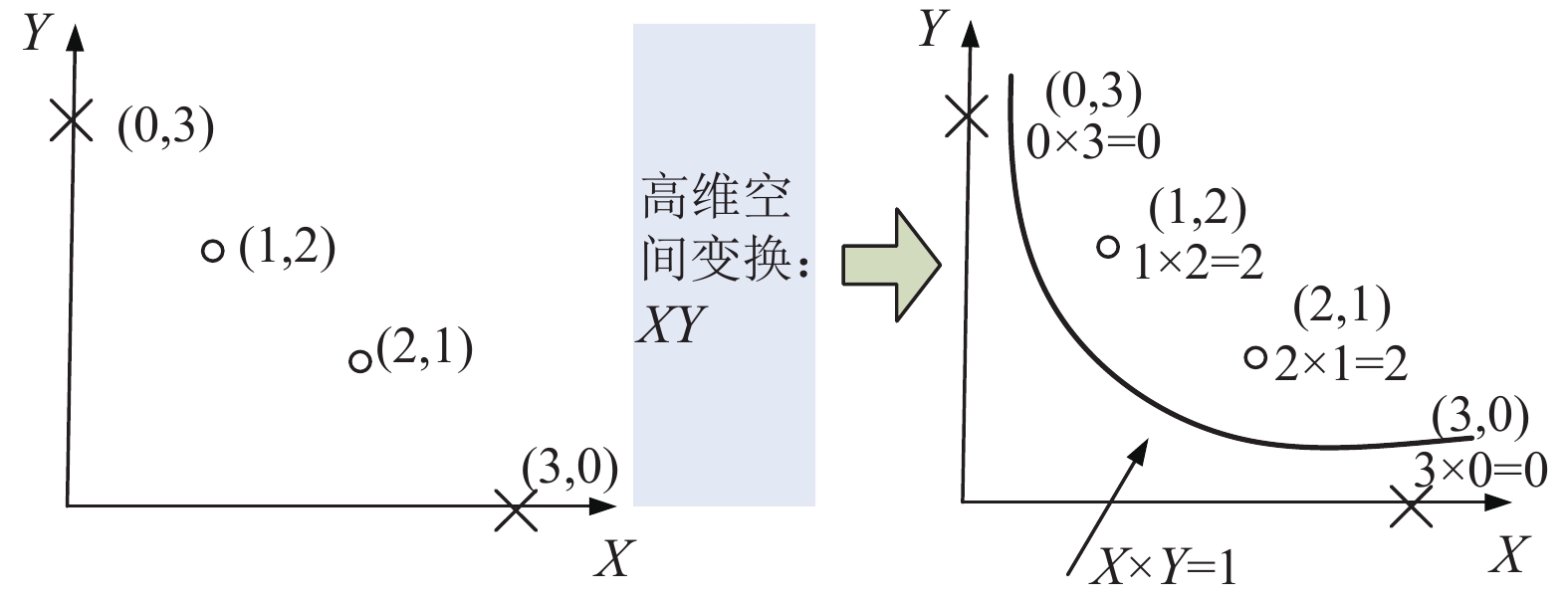
假设原始样本点的特征信息量化表示为(0, 3)、(1, 2)、(2, 1)、(3, 0),那么从图1(左)可以直观看出无法正确区分其类别,因此利用非线性变换函数包括
$x + y$ ,$xy$ 以及${x^2}$ 进行高维空间的计算,利用$xy$ 的变换能够得到两类不一样的计算特征,包括$xy = 2$ ,和$xy = 0$ ,那么利用曲线$xy = 1$ 就能够成功的将标记为2和标记为1的两类目标进行分类,如图1(右)所示。3. 实例验证分析
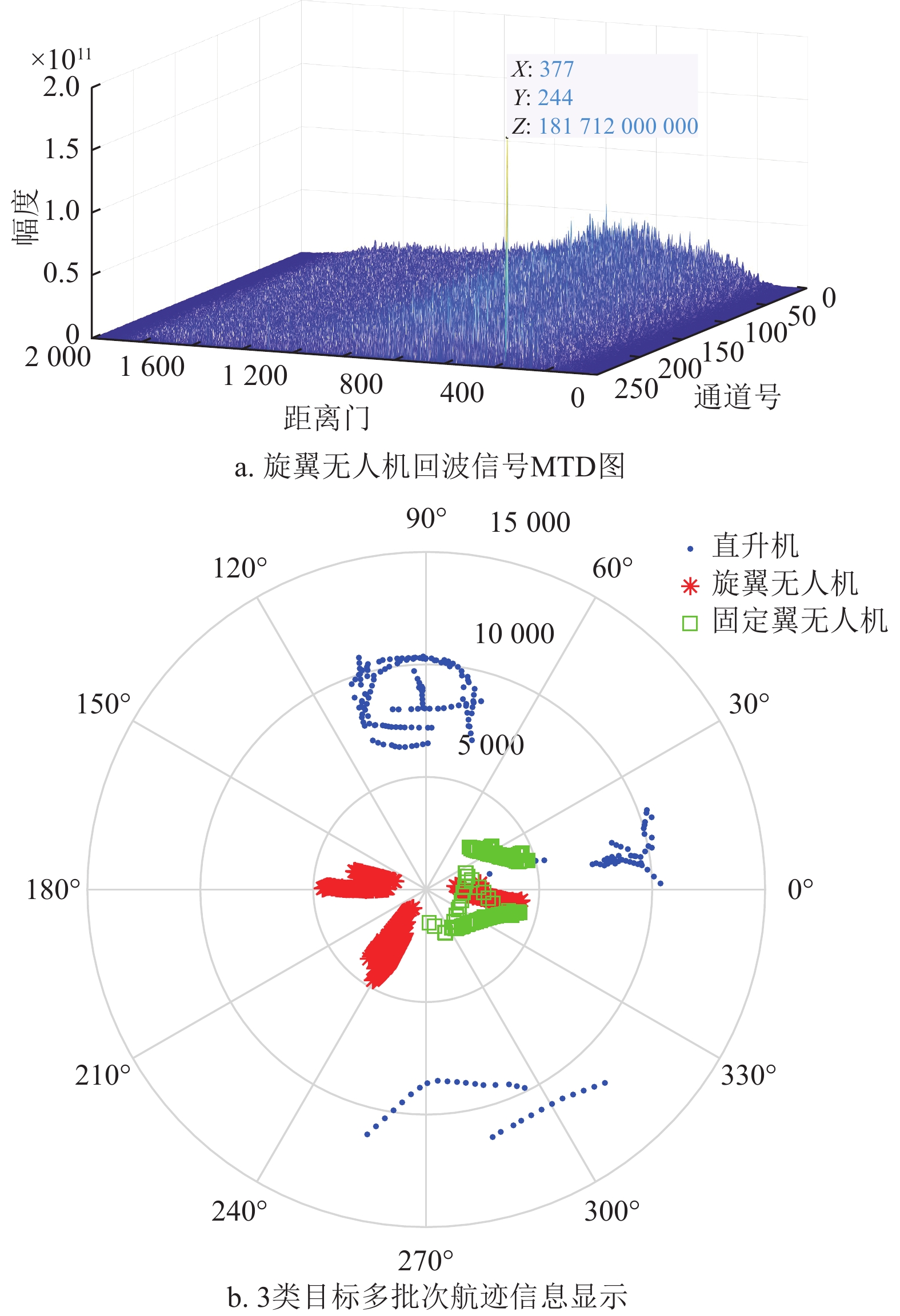
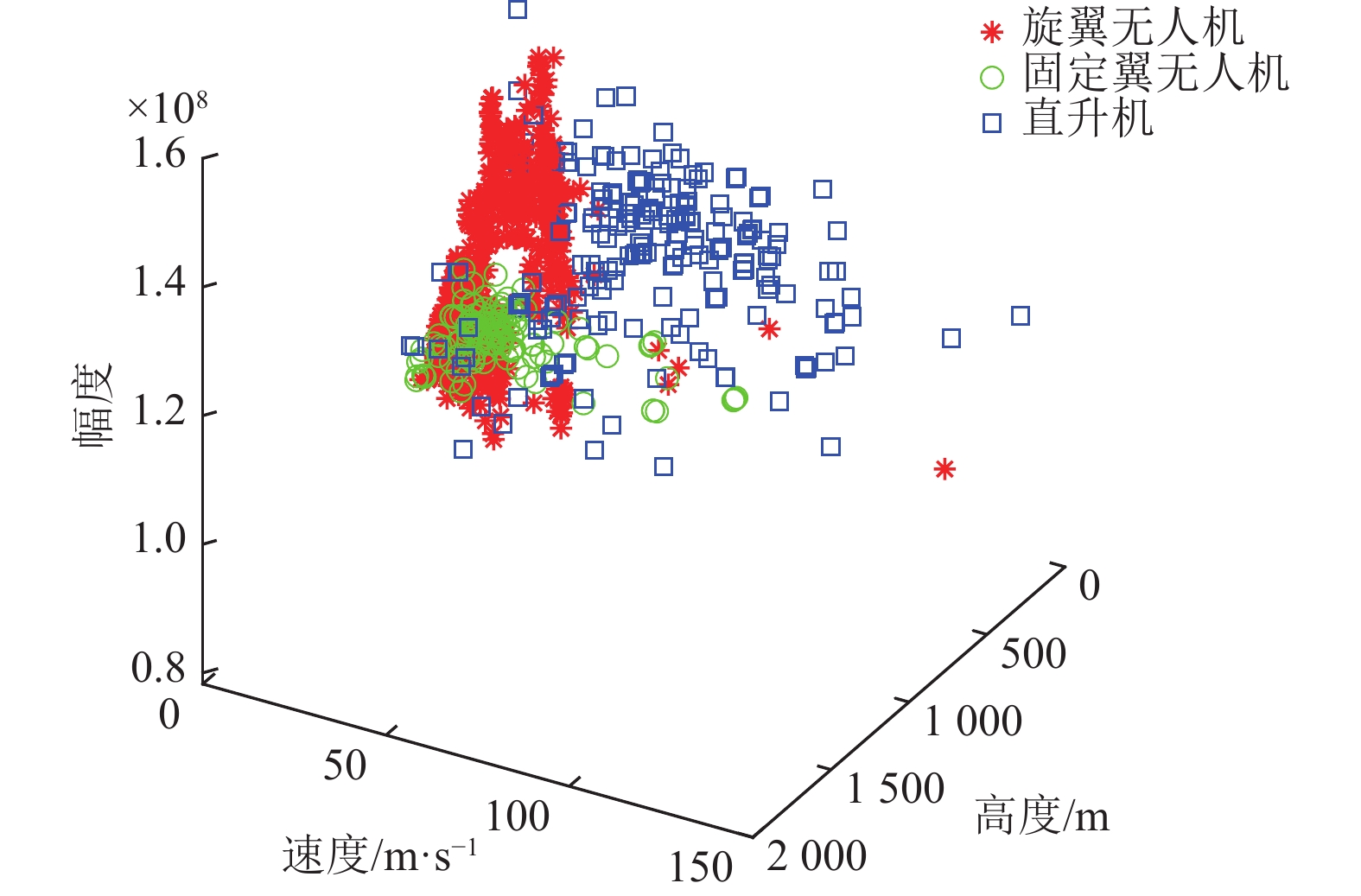
采集包含低空小微目标的雷达回波和航迹数据,如图2所示,提取目标信号及航迹信息。分析小微目标的高度-速度-幅度特征的态势分布,如图3所示,常规属性特性分布较为相似,交织严重,采用属性区间判别的方式,分辨概率低,为了能够高效、准确的实现旋翼无人机、固定翼无人机以及直升机的分类判别,因此,构建包含信号特征以及航迹拟合特征的稳健特征组合,通过线性变换和非线性变换建立高维特征域,最终利用多层级的学习树模型以实现最终的目标分类判别[10-13]。
1)按照前面介绍的信号特征模型进行计算并提取目标一系列信号特征:相位
${x_1}$ 、频率熵${x_2}$ 、能量比${x_3}$ 、幅值强度$ {x_4} $ ,形成信号特征组合:$$ {\boldsymbol{X}} = ({x_1},{x_2},{x_3},{x_4}) $$ 2)按照前面介绍的航迹特征模型进行计算并提取目标一系列航迹特征:拟合误差均值
$ {f_1} $ 、拟合误差方差$ {f_2} $ 、距离均值$ {f_3} $ 、距离差的最大值$ {f_4} $ 、最小值和最大值的比值$ {f_5} $ 、加速度的均值$ {f_6} $ 、加速度的方差$ {f_7} $ 、加加速度的均值$ {f_8} $ 、加加速度的方差$ {f_9} $ 、速度$ v $ 、高度$ h $ 、距离$ R $ ,形成航迹特征组合:$$ {\boldsymbol{F}}=({f}_{1},{f}_{2}\text{,}{f}_{3}\text{,}{f}_{4},{f}_{5}\text{,}{f}_{6},{f}_{7},{f}_{8}\text{,}{f}_{9},v,h,R) $$ 3)高维特征域获取
利用线性变换、非线性变换等对信号特征和航迹特征进行联合处理,形成高维特征域。对信号特征和航迹特征进行线性变换:
$$ {\boldsymbol{A}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{a_{11}}}&0& \cdots &0 \\ 0&{{a_{22}}}& \cdots &0 \\ 0&0& \ddots &0 \\ 0&0& \cdots &{{a_{nn}}} \end{array}} \right] $$ 利用矩阵
$ {\boldsymbol{A}} $ 对对信号特征$ {\boldsymbol{X}} $ 和航迹特征$ {\boldsymbol{F}} $ 分别进行拉伸和剪切变换,其中$ a_{ij}^{} \in [0,\infty ] $ ,得到新的两组特征组合:$$ {\boldsymbol{X}}_{\boldsymbol{1}}^{}{\boldsymbol{ = A*X}} , {\boldsymbol{F}}_{\boldsymbol{1}}^{}{\boldsymbol{ = A*F}} $$ 对联合特征组合进行求积、求和等非线性变换。
内积运算:
$$ \begin{gathered} {\boldsymbol{X}}_{\boldsymbol{2}}^{}{\boldsymbol{ = }}{{\boldsymbol{X}}_{\boldsymbol{1}}} \cdot {\boldsymbol{X}}_{\boldsymbol{1}}^{} \\ {\boldsymbol{F}}_{\boldsymbol{2}}^{}{\boldsymbol{ = }}{{\boldsymbol{F}}_{\boldsymbol{1}}} \cdot {{\boldsymbol{F}}_{\boldsymbol{1}}} \\ {\boldsymbol{S}}_{\boldsymbol{1}}^{}{\boldsymbol{ = }}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{X}}_{\boldsymbol{1}}}}&{{{\boldsymbol{X}}_{\boldsymbol{2}}}} \end{array}} \right]{{\boldsymbol{F}}_{\boldsymbol{2}}} \\ \end{gathered} $$ 和运算:
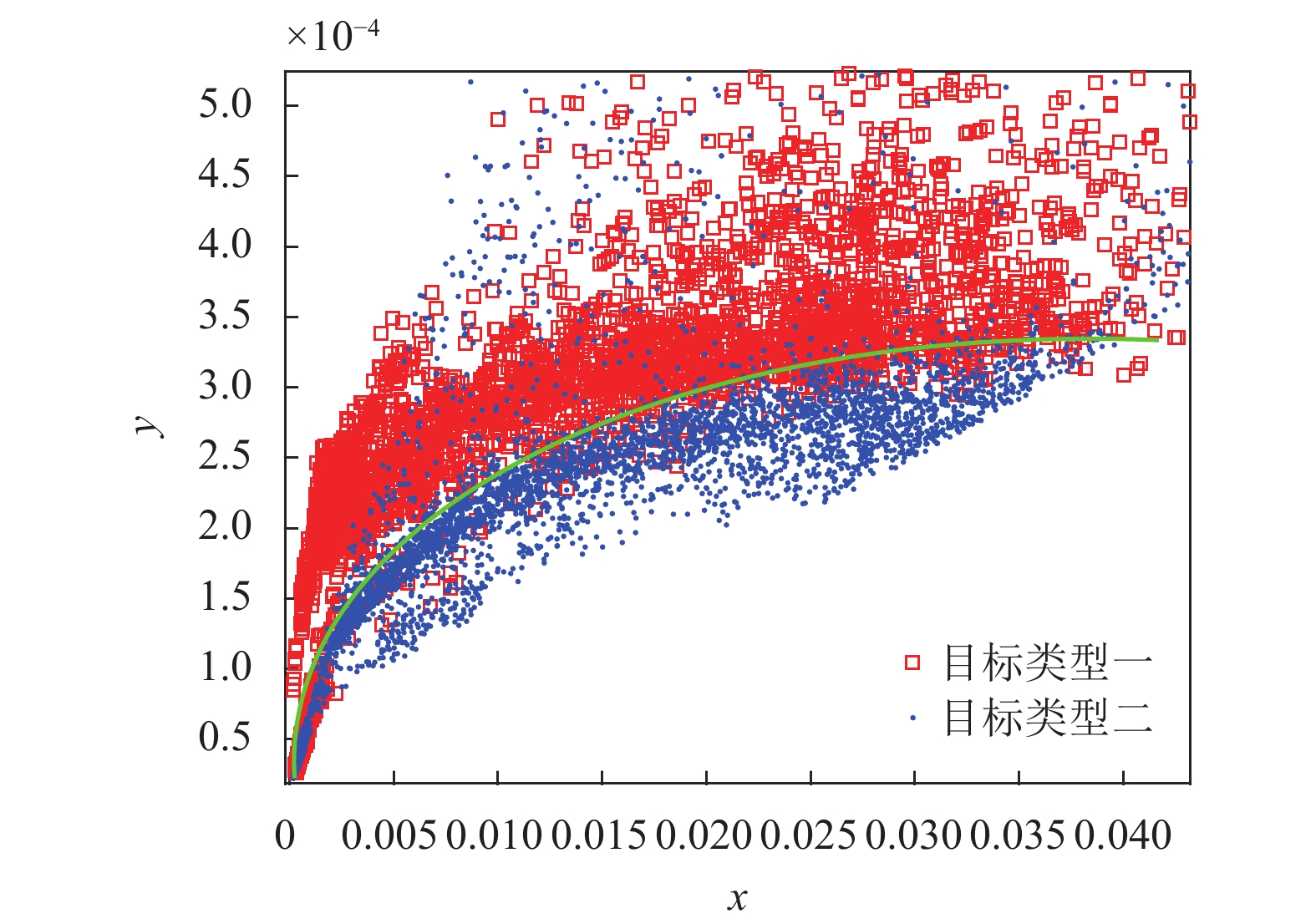
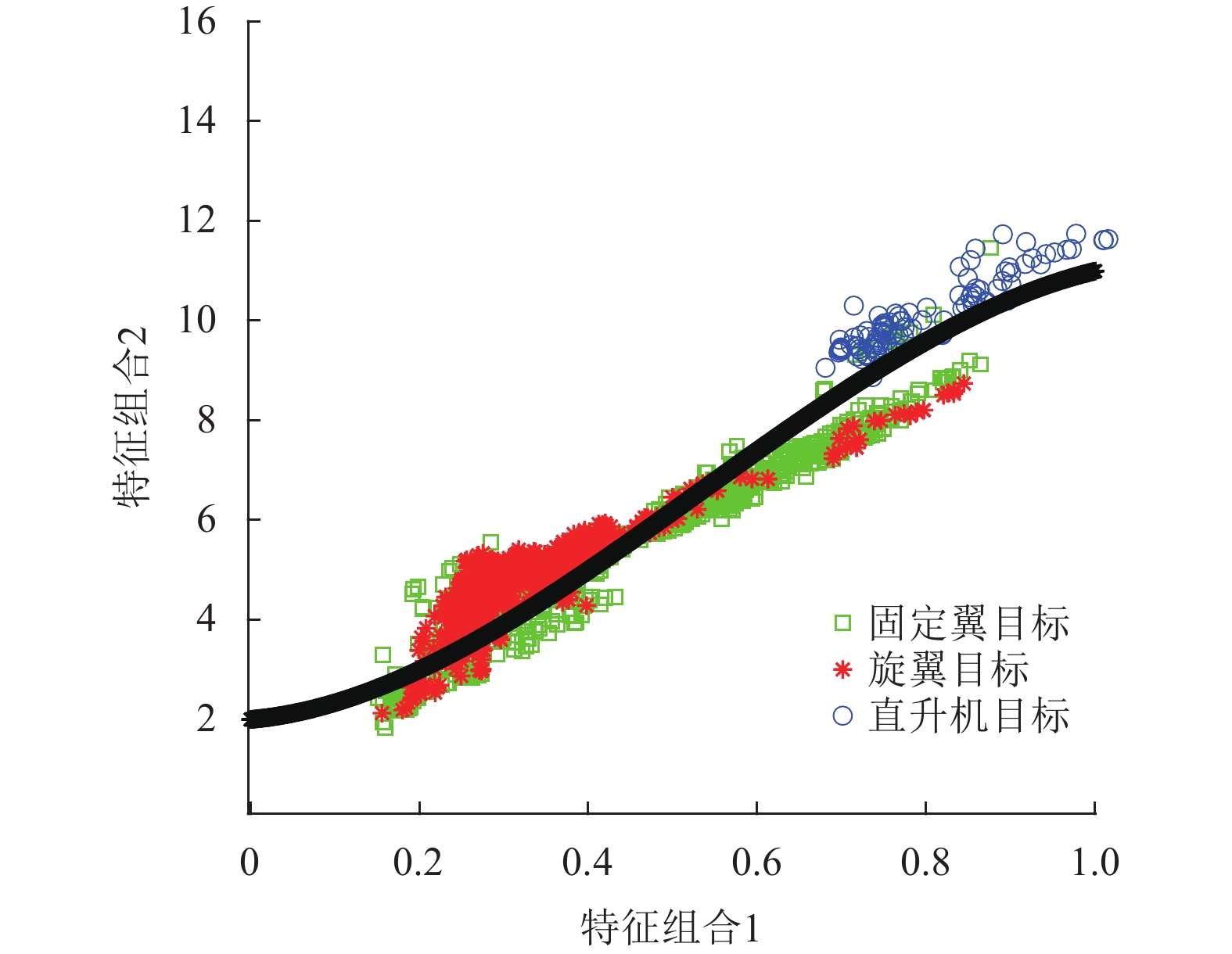
$$ {\boldsymbol{S}}_{\boldsymbol{2}}^{} = \sum\limits_{i = 1}^4 {{{\boldsymbol{X}}_{\boldsymbol{1}}}} + \sum\limits_{i = 1}^{12} {{{\boldsymbol{F}}_{\boldsymbol{1}}}} \quad{\boldsymbol{S}}_{\boldsymbol{3}}^{} = \sum\limits_{i = 1}^4 {{{\boldsymbol{X}}_{\boldsymbol{2}}}} + \sum\limits_{i = 1}^{12} {{{\boldsymbol{F}}_2}} $$ 利用实测的关注目标点迹和航迹数据通过线性变换和非线性变换后可获取高维特征域,在一种新模态下呈现出可分的态势,如图4所示。
4)仿真验证
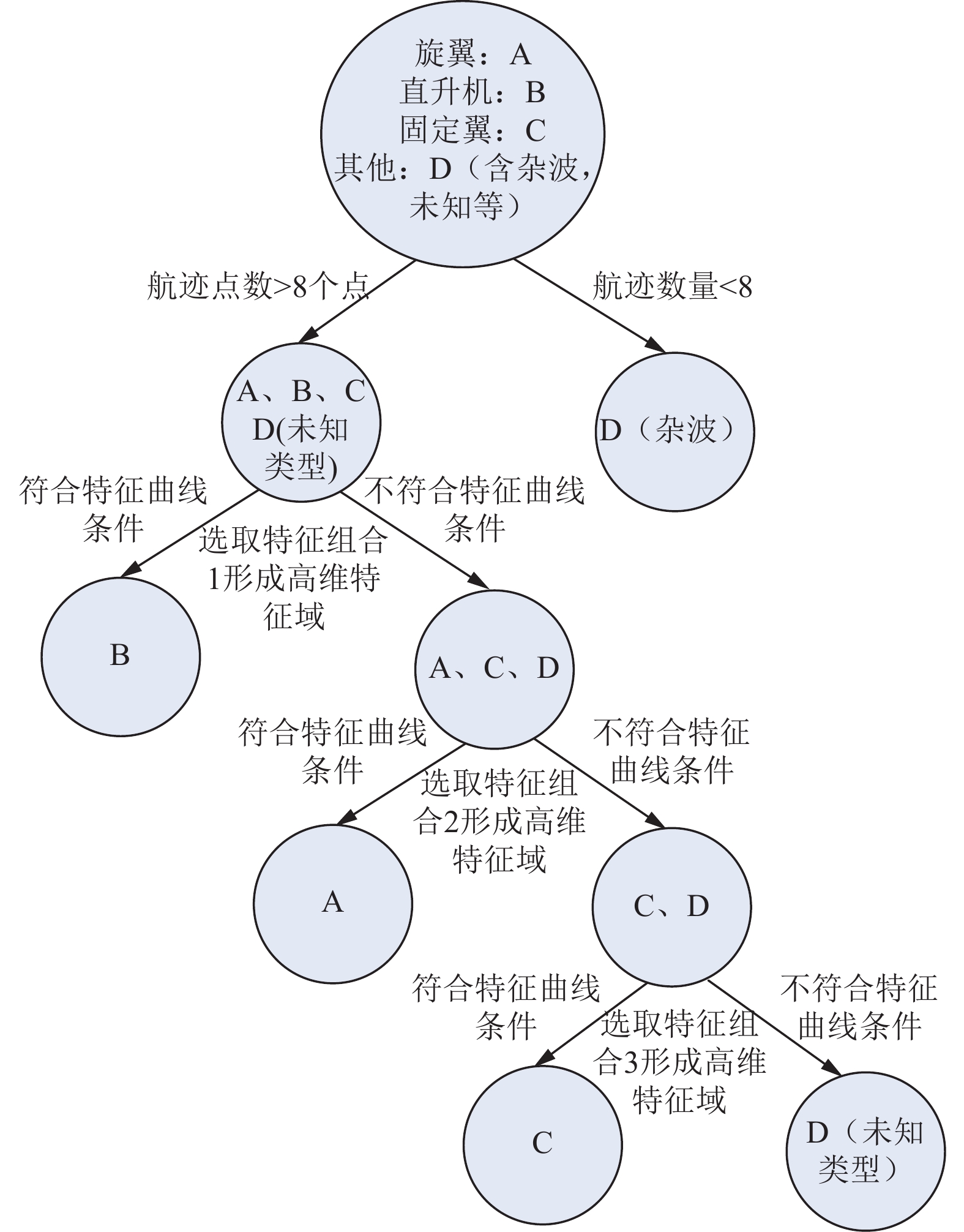
建立多层级学习树网络模型,针对每一层级关注的类型选择基本特征组建高维特征域,利用拟合分类曲线实现二分类模型的设计,如图5所示。分类实施过程中首先二分类虚假目标和关注目标,然后逐层实现旋翼无人机、直升机、固定翼以及未知类型小微目标的分类。
针对旋翼、固定翼和直升机的分类问题,分别计算并取出包含目标的4维物理特征
$ {\boldsymbol{X}} = ({x_1}, {x_2},{x_3},{x_4}) $ 和12维航迹特征$ F=({f}_{1},{f}_{2}\text{,}{f}_{3}\text{,} {f}_{4},{f}_{5}\text{,} {f}_{6},{f}_{7}, {f}_{8}\text{,} {f}_{9},v,h,R) $ 的点迹数据。从一组旋翼无人机目标点迹数据中提取一列数据并取出包含以上16维特征信息形成特征向量
$ {\bf{data}}1 $ :[97, 11, 2.2,99097242 ,0.0022 ,0.0006 ,0.0040 ,1.7371 ,1.7449 ,1537.83 ,46.3073 ,0.6349 , 271.808,1439 , 149,13]。从一组直升机目标点迹数据中提取一列数据并取出包含以上16维特征的信息形成特征向量
$ {\bf{data}}2 $ :[88, 35, 1.3,119330748 ,0.0005 , −0.0002 ,0.0008 ,0.6558 ,0.6638 ,7298.14 , 300.124,0.4135 ,1343.95 ,7437 , 280, 26]。从一组固定翼目标点迹数据中提取一列数据并取出包含以上16维特征的信息形成特征向量
$ {\bf{data}}3 $ : [86, 53, 1.7,113567082 ,0.0020 ,0.0002 ,0.0035 , −0.2397 ,0.2399 ,2992.12 , 125.17,0.5181 , 659.105,2750 , 814, 26]。从单个点迹数值上看,3类目标速度、高度均较为一致,难以准确地完成分类处理,采用某低分辨雷达采集的多组试验数据(包含旋翼、固定翼、直升机3类关注小微目标),将数据统一进行归一化处理,从以上试验数据总的点迹库中分别提取16维特征对应的最大值序列
$ {{{x}}_{\max }} $ 和最小值序列$ {{{x}}_{\min }} $ ,最大值序列$ {{{x}}_{\max }} $ 表示为 [1897 ,12413 ,3.700 ,5.455 ×1021,0.039 ,0.014 ,0.034 ,59.572 ,249.163 ,16129.577 ,1501.974 ,0.987 ,3964.310 ,16642 ,1809 , 145]。最小值序列$ {{{x}}_{\min }} $ 表示为[0, 0, 0,78255702 , 0, −0.017, 0, −58.259, 0, 0, 0, 0, 0, 419, 5, −22.805]。按照
${X_{{\text{norm}}}} = \dfrac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}$ 将数值进行归一化表示,从16维归一化特征中取出速度、高度、航迹拟合、幅度等一系列的特征形成特征组合向量$ {{\boldsymbol{X}}_1} $ :[0.0137 ,0.4291 ,1.4497 , −1.4346×10−14, −1.4346×10−14,0.0573 ,0.0217 , −1.4346×10−14,0.0449 ,0.6484 ]。$$ \begin{gathered} \quad\quad\quad\quad\quad{{\boldsymbol{A}}_{\mathbf{1}}}{\text{ = }}\left[ \begin{array}{*{20}{c}} {\text{1}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{1}}&{\text{0}} \\ {\text{0}}&{\text{0}}&1.1564 \times{10^{-11}} \end{array} \right] \\ {{\boldsymbol{A}}_{\mathbf{2}}}{\text{ = }}\left[ \begin{array}{*{20}{c}} {\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{{\text{0}}{\text{.0573}}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{{\text{0}}{\text{.0573}}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{{\text{0}}{\text{.0217}}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{{\text{30000}}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{8}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{{\text{10}}} \end{array} \right] \end{gathered} $$ 分别利用
${{\boldsymbol{A}}_{\boldsymbol{1}}}$ 和${{\boldsymbol{A}}_{\boldsymbol{2}}}$ 对数据进行线性变换和非线性变换,得到高维域下目标点迹坐标为:$$ \begin{split} &\overline {{\bf{data}}} {\boldsymbol{1}} = (0.293, 2.778) \\ &\overline {{\bf{data}}} {\boldsymbol{2}} = (0.393,3.951) \\ &\overline {{\bf{data}}} {\boldsymbol{3}} = (0.739,6.531) \end{split} $$ 从数值上便可将旋翼和其他两类目标进行有效区分。
为了进一步验证该方法的有效性,利用某低分辨雷达采集的多组试验数据,包含旋翼、固定翼、直升机3类关注小微目标共26批次,总点迹数量为
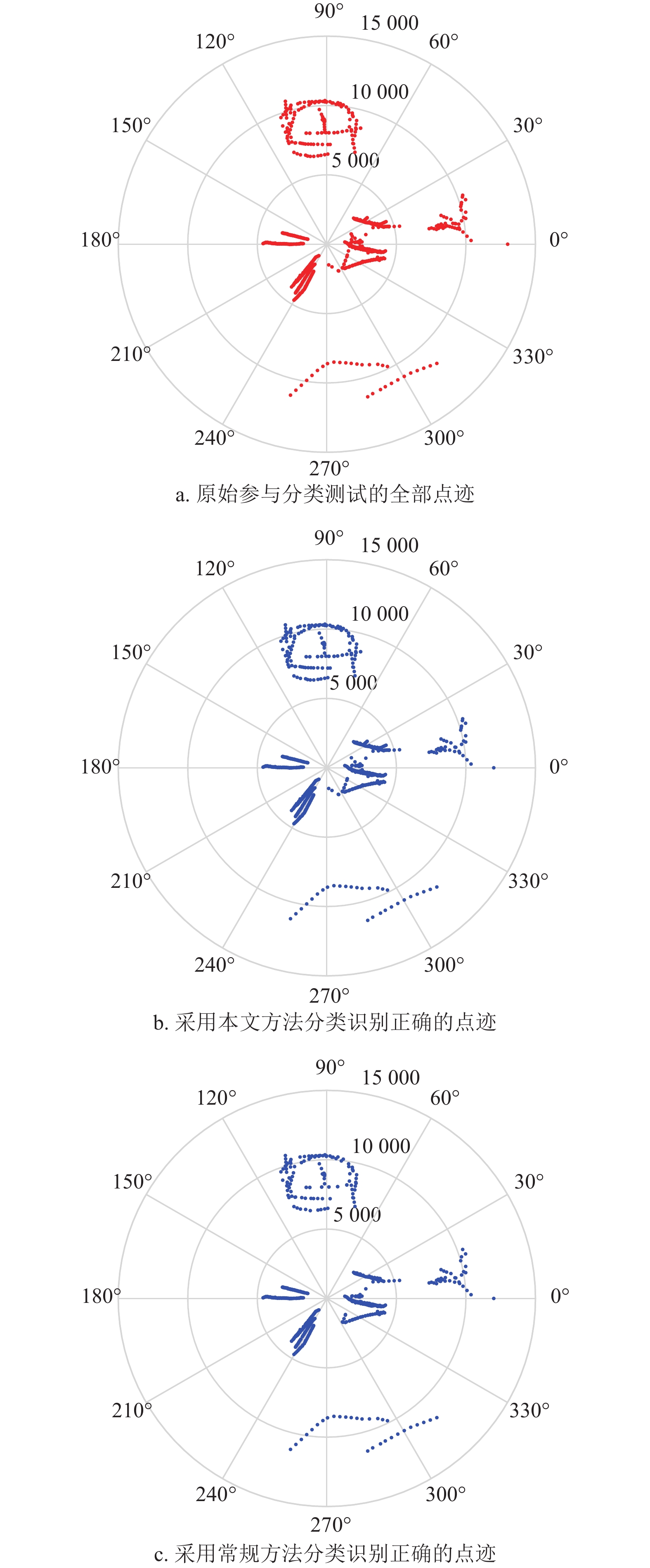
1795 ,分别采用基于目标属性经验区间判别方法和多组分类线对3类目标进行多层级网络的分类测试与筛选对比验证,其中经验区间设定为直升机速度$ \in [45,80]\;{\mathrm{m/s}}$ ,直升机幅度$ > 160\;{\mathrm{dB}}$ ,旋翼无人机速度$ \in [0,30]\;{\mathrm{m/s}}$ ,旋翼无人机高度$ \in [50,400]\;{\mathrm{m}}$ ,固定翼速度$ \in [25,65]\;{\mathrm{m/s}}$ ,固定翼高度$ \in [400,800]\;{\mathrm{m}}$ ;分类曲线则是利用幅度、速度、航迹拟合等特征组合以及高维域变换建立3类目标进行分类处理,其中1种组合特征分类曲线如图6所示。对比测试以上两种分类方法,分类判别结果如图7所示,采用常规属性区间判别方法分类正确的点迹数量为
1332 ,分类正确率74%,本文方法的正确点迹数量为1723 ,分类识别正确率大于95%。4. 结束语
本文通过对某型雷达的含有关注小微目标原始回波信号进行分析和微观特征的提取,结合航迹宏观特征建立联合特征域,针对小微目标特征分布态势交织严重、分辨准确率低等问题,采用线性变换和非线性变换提升特征的维度,获取高维特征域,最后建立由粗到细的多层级学习树网络模型,实现多类小微目标的准确分类识别。试验结果表明该方法能准确、有效地实现小微目标的分类识别。
-
[1] DAGHOUJ D, ABDELLAOUI M, FATTAH M, et al. Automatic target recognition based on the features of UWB radar signals[J]. International Journal on Engineering Applications (IREA), 2021, 9(6): 310. DOI: 10.15866/irea.v9i6.19590
[2] 施赛楠, 杨静, 董泽远. 基于高维特征域随机森林的海面小目标检测[J]. 现代雷达, 2022, 44(3): 63-69. SHI S N, YANG J, DONG Z Y. Detection of small sea-surface target based on random forest in high-dimensional feature domain[J]. Modern Radar, 2022, 44(3): 63-69.
[3] 吴琳拥, 毛谨, 白渭雄. 基于奇异值分解的雷达微小目标检测方法[J]. 电子科技大学学报, 2019, 48(3): 326-330. DOI: 10.3969/j.issn.1001-0548.2019.03.002 WU L Y, MAO J, BAI W X. Radar small target detection based on singular value decomposition method[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(3): 326-330. DOI: 10.3969/j.issn.1001-0548.2019.03.002
[4] XU S W, ZHU J N, SHUI P L, et al. Floating small target detection in sea clutter by one-class SVM based on three detection features[C]//Proceedings of the International Applied Computational Electromagnetics Society Symposium. Nanjing: IEEE, 2019: 1-2.
[5] ZHAO Q, LIU H, LU Y. A method of aircraft target recognition for meter wave-radar based on convolutional neural network[C]//Proceedings of the IET International Radar Conference. London: IET, 2020: 1205-1210.
[6] NANZER J A, ROGERS R L. Bayesian classification of humans and vehicles using micro-Doppler signals from a scanning-beam radar[J]. IEEE Microwave and Wireless Components Letters, 2009, 19(5): 338-340. DOI: 10.1109/LMWC.2009.2017620
[7] CHEN F, LIU H W, DU L, et al. Target classification with low-resolution radar based on dispersion situations of eigenvalue spectra[J]. Science China Information Sciences, 2010, 53: 1446-1460. DOI: 10.1007/s11432-010-3099-5
[8] 向凡夫, 郝冬青, 吴鹏. 针对低慢小目标的雷达信号处理算法[J]. 指挥控制与仿真, 2019, 41(4): 40-46. DOI: 10.3969/j.issn.1673-3819.2019.04.009 XIANG F F, HAO D Q, WU P. Radar signal processing algorithm for low altitude slow speed and small target[J]. Command Control & Simulation, 2019, 41(4): 40-46. DOI: 10.3969/j.issn.1673-3819.2019.04.009
[9] 王伟, 张汉华, 姜卫东, 等. 低分辨雷达的目标特征提取方法[J]. 国防科技大学学报, 2002, 24(2): 31-35 DOI: 10.3969/j.issn.1001-2486.2002.02.009 WANG W, ZHANG H H, JIANG W D, et al. The study of target feature extracting method based on low-resolution radar[J]. Journal of National University of Defense Technology, 2002, 24(2): 31-35. DOI: 10.3969/j.issn.1001-2486.2002.02.009
[10] 黄小红, 贺夏, 辛玉林, 等. 基于时频特征的低分辨雷达微动多目标分辨方法[J]. 电子与信息学报, 2010, 32(10): 2342-2347. HUANG X H, HE X, XIN Y L, et al. Resolving multiple targets with micro-motions based on time-frequency feature with low-resolution radar[J]. Journal of Electronics & Information Technology, 2010, 32(10): 2342-2347.
[11] 陈海峰, 冯源. 基于CNN的雷达目标分类识别技术研究[J]. 现代雷达, 2022(4): 38-43. CHEN H F, FENG Y. A study on radar target classidication and recognition technology based on CNN[J]. Modern Radar, 2022(4): 38-43.
[12] 朱克凡, 王杰贵. 小样本条件下SCGAN+CNN低分辨雷达目标一步识别算法[J]. 系统工程与电子技术, 2020, 42(1): 67-75. DOI: 10.3969/j.issn.1001-506X.2020.01.10 ZHU K F, WANG J G. Low resolution radar target one-step recognition algorithm based on SCGAN+CNN with a limited training data[J]. Systems Engineering and Electronics, 2020, 42(1): 67-75. DOI: 10.3969/j.issn.1001-506X.2020.01.10
[13] 晏媛, 孙俊, 孙晶明, 等. 雷达小样本目标识别方法及应用分析[J]. 系统工程与电子技术, 2021, 43(3): 684-692. DOI: 10.12305/j.issn.1001-506X.2021.03.11 YAN Y, SUN J, SUN J M, et al. Radar few shot target recognition method and application analysis[J]. Systems Engineering and Electronics, 2021, 43(3): 684-692. DOI: 10.12305/j.issn.1001-506X.2021.03.11

 ISSN
ISSN 


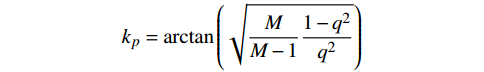
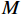
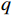
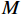
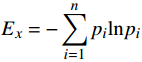
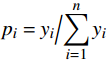
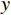


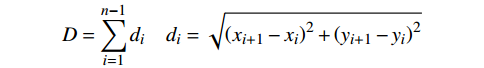
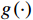
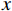
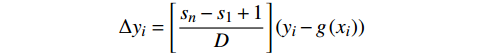
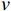
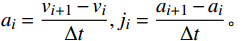
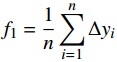
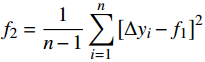
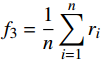

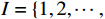
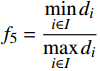
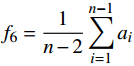
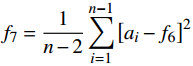
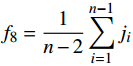
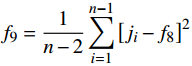
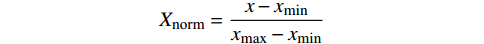
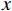
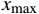
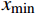
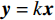
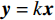
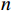
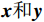
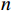
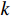
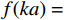
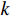
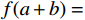
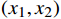
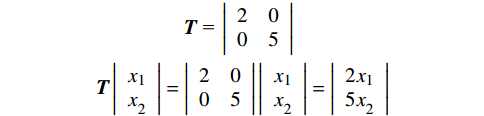
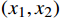
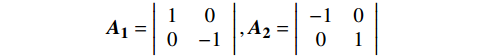
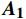
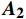
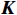
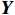
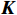
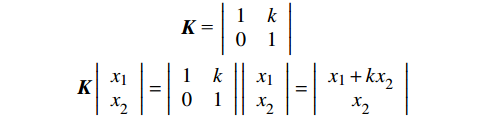
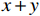
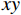
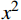
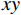
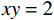
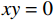
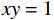
 下载:
下载: