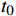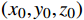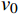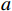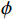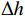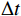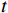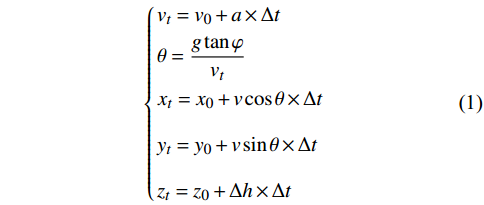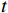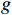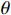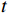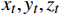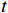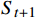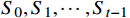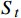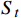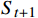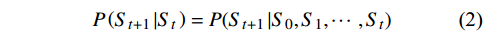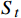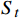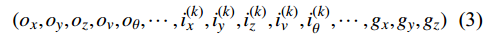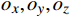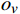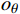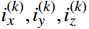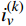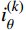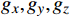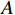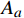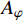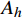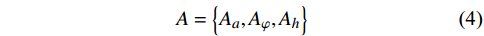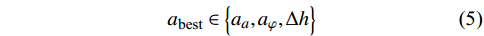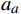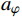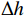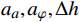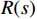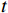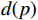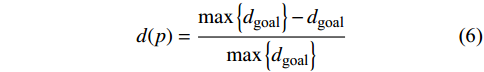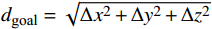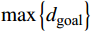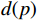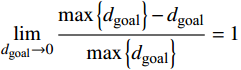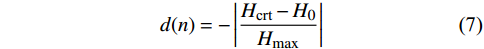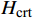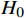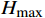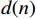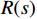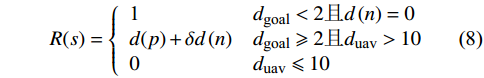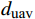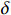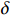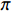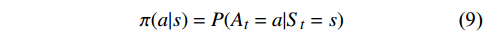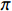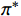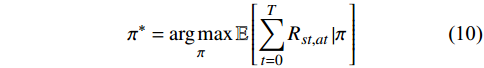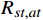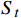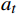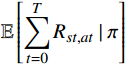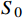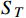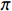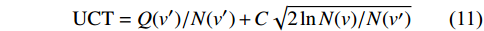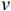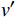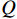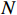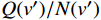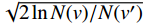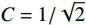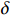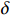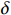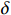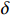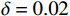Collision avoidance algorithm for urban low-altitude UAV with limited sense system
-
摘要:
针对物流无人机在城市低空复杂环境和高密度动态交通流下的避障决策问题,提出一种动态三维避障算法。首先对城市低空环境建模并将无人机的动态避障问题表达为马尔可夫决策过程,通过在动作集中加入高度变化等飞行动作,将避障算法可行解的范围拓展到三维空间中。其次改进了奖励估值函数,使算法能够在绕飞以及爬升越障中通过蒙特卡罗树搜索权衡最优避障策略。仿真表明该算法能够选择最优策略,缩短24.4%的飞行时间并减少33.2%的飞行距离。最后考虑到无人机感知系统容易因建筑物遮挡受限而造成对环境状态观测不完全,对算法鲁棒性做出了验证,其结果表明随着感知范围缩短,算法仍能求得可行解。
Abstract:Aiming at the collision avoidance problem of logistics unmanned aerial vehicle in the complex urban low-altitude environment and high-density dynamic traffic flow, a dynamic three-dimensional (3D) collision avoidance algorithm is proposed. Firstly, we model the urban low altitude operating environment, express the dynamic collision avoidance problem of unmanned aerial vehicle as a Markov decision process, and expand the feasible solution range of algorithm to the 3D space by adding the altitude change and other manoeuvre into the action set of collision avoidance. Secondly, we improve the reward valuation function, so that the algorithm can balance the optimal decision by Monte Carlo tree search in two-dimensional plane flying around and 3D space obstacle crossing. Finally, the global optimal solution is gradually obtained by approaching the single optimal feasible solution. The simulation results show that the algorithm can optimize the collision avoidance action, and choose the best collision avoidance strategy in flying around and crossing obstacles to shorten the flight time by 24.4% and reduce the flight distance by 33.2%. For the unmanned aerial vehicle operating in the urban low-altitude environment, its sense system is easy to be partially observable due to the limited building occlusion, and the algorithm cannot obtain sufficient environmental state information input for solution calculation, so the algorithm requires robustness. The simulation results show that with the shortening of sense radius, the algorithm has good performance and can still give most of the feasible solutions under the limited conditions of the unmanned aerial vehicle sense system.
-
目前,无人机逐步被用于解决城市低空场景下“最后一公里”配送效率低下的问题[1]。美团、饿了么、迅蚁等利用无人机,在深圳、上海等多个城市解决即时物流配送问题。政策方面,有关部门颁布了一系列文件促进了无人机在城市场景下的应用[2-3]。城市低空场景下运行的无人机将面临更加复杂的空域环境,为保证无人机航行安全需要具有可靠的环境状态感知和实时在线的避障决策技术。
文献[4]首次提出碰撞锥的概念,基于几何方法解决运动体的避撞问题。2020年,文献[5]提出碰撞锥结合微分几何的思路求解避障轨迹,但是该算法中的无人机只能在恒定速度下以固定姿态进行避障。2023年,文献[6]在碰撞锥的基础上结合无人机防撞预警准则以及相对运动学模型,提出了一种反应式防撞和轨迹恢复策略。文献[7]提出速度障碍法解决多智能体的动态避撞问题。2019年,文献[8]针对速度障碍法的多种改进方法进行了分析对比,给出了改进算法的适用范围和缺陷。2020年,文献[9]为解决动态避障中采用速度障碍法产生的双曲线误差,提出金字塔锥法的概念,保证了避撞飞行路径的光滑和可飞性,但建模方法具有一定的局限性。为解决高维空间和复杂约束条件下智能体的路径规划问题, 文献[10]提出采用基于空间采样的快速扩展随机树(rapidly exploring random tree, RRT)算法。2019年,文献[11]通过对RRT算法生成的最终路径进行了平滑和修正优化了避障路径,但是该算法仅限于静态三维环境下的避障。文献[12]提出人工势场法,通过在环境中构建虚拟势场引导智能体避障,该方法具有较强的实时性且对计算性能的要求较低。2023年,文献[13]在人工势场法的基础上引入位置斥力和速度斥力并加入阻尼系数解决势场法易陷入局部最优的问题,但其解脱过程耗时较长,难以适用于轻小型无人机要求的短时快速避障。随着机载性能提高,智能算法被应用在无人机避障中。2019年,文献[14]提出采用压缩深度神经网络以优化避障策略,提高了无人机避障效率,但该算法只适用于集中式无人机避障。2020年,文献[15]提出深度高斯过程进行飞行冲突探测,但该算法依赖于历史航迹,算法泛化性有限。对于运动体避障问题,常采用强化学习方法解决[16-17]。2023年,文献[18]提出分层深度强化学习方法,将无人机避障问题分解为动态避障和路径规划两个子模型,降低了模型训练难度,但算法局限于简单二维场景的实时避障。
无人机通过感知系统,如双目摄像头、激光雷达等传感器来探测周围环境,机载计算机根据获得的环境信息求解最优飞行动作,在控制无人机飞行的同时将会实时更新环境信息,并继续求解下一步飞行动作。无人机通过执行不同的飞行动作不断与周围环境进行交互,从而接近目标点。智能体通过与环境之间交互从而做出最优决策的行为,这符合强化学习框架,因此本文考虑采用强化学习对无人机避障问题求解。
现有算法大多未考虑到城市低空的特殊环境对轻小型无人机所造成的影响,如高密度的空域环境、狭窄的飞行空间、高层建筑遮挡所形成的探测盲区等,因此易导致感知系统对环境的观测不完全,使得算法无法求解。为减少探测盲区对无人机避障的影响,充分利用感知系统获取的周围环境状态信息,本文基于强化学习理论设计出一种三维避障算法,并利用蒙特卡罗树搜索计算全局最优解或近似最优解。仿真结果表明在感知系统探测范围受到限制的情况下,该算法仍能满足无人机避障所需性能。
1. 问题描述及环境建模
1.1 运行环境及避障策略
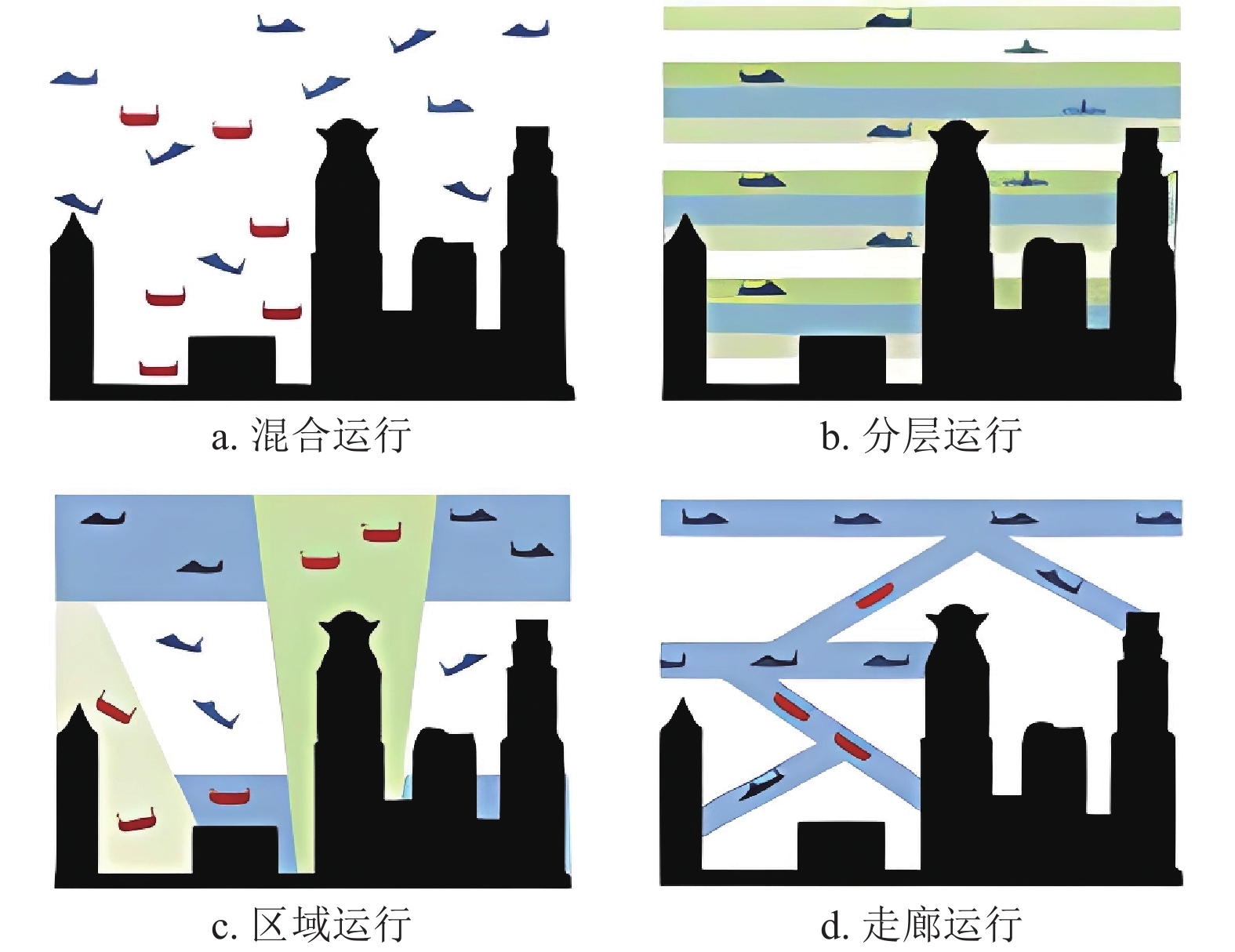
目前,学术界普遍认为对于城市低空环境下的无人机应该运行在如图1所示中的4种可能空域结构中[19]。
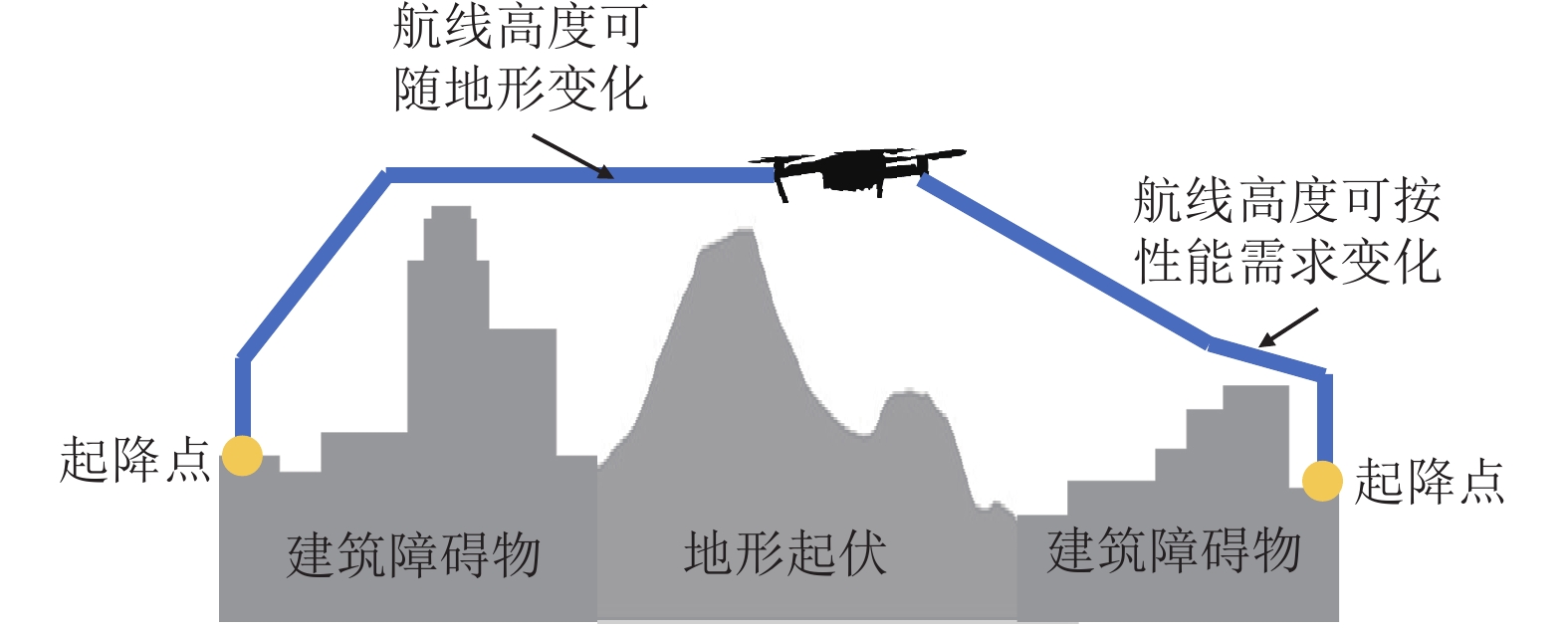
以上4种空域结构中,图1b分层运行模式被证明是在保证效率的情况下,空中冲突概率最低的一种空域结构[20],这种结构化的超低空空域飞行高度层垂直范围通常在真高40~120 m之间[21],无人机在进入巡航阶段后,除非需要进行避障否则应尽量保持在某一设定的高度层上进行飞行[22],如图2所示。
障碍物按照其运动特征分为动态障碍及静态障碍。根据分层运行规则,城市低空飞行的无人机对于不同类型的障碍将会采取不同避障策略。对于空中交通流或其他运动体等动态障碍,主要采取保持高度在水平方向机动进行避障;对于地形或建筑物等静态障碍可根据无人机性能冗余、安全超障高度并结合时间成本求解最优避障决策,选择水平绕飞或爬升越障后再回到初始高度。本文设计的算法将按照此策略来控制无人机避障。
1.2 仿真模型描述
1.2.1 环境模型定义
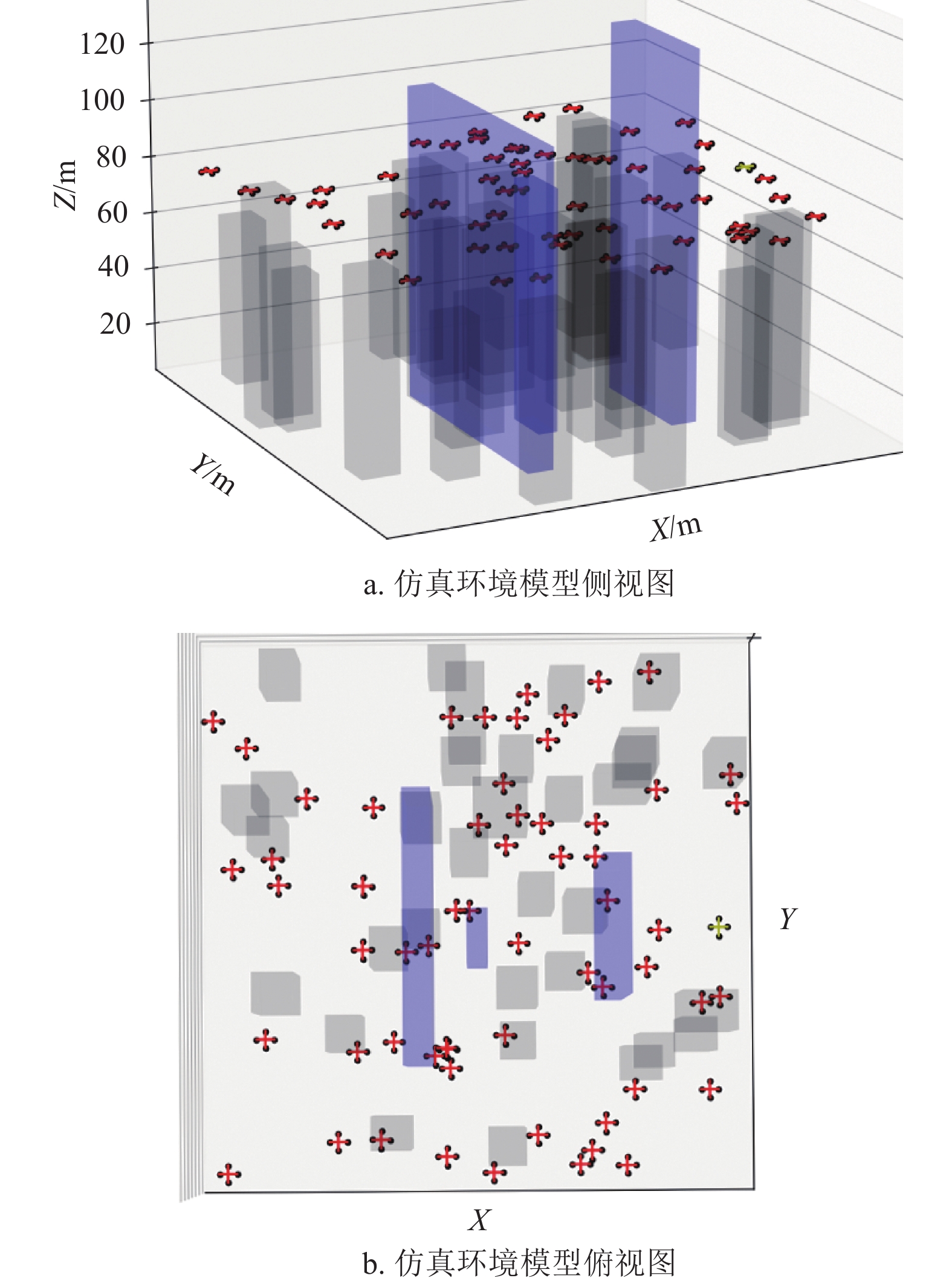
本文通过建立三维空间环境模型将无人机限制在一个有限的连续空间并对该空间进行栅格化处理。文中的长方体表示静态障碍所形成的不可飞区域,如图3所示。本模型中黑色立体图形块表示高度不超过70 m的静态障碍,蓝色立体图形块表示高度大于70 m的静态障碍;其中黄色图形代表具有本文所设计的避障算法的无人机;红色图形代表动态障碍,本文规定这类动态障碍沿直线匀速运动且不会主动进行避让,本文中将这类动态障碍称为“入侵机”。
根据中国民航局发布的技术标准要求[23],城市场景下的轻型无人机最大平飞速度可达100 km/h,为保留较大的安全冗余将无人机之间的安全距离定义为10 m,小于该安全距离则认为产生空中冲突。
1.2.2 无人机运动模型
已知
$ {t}_{0} $ 时刻无人机的状态量参数:初始位置坐标$ \left({x}_{0},{y}_{0},{z}_{0}\right) $ 、初速度$ {v}_{0} $ 、加速度$ a $ 、倾斜角$ \phi $ 、高度变化率$ \Delta h $ 以及邻近状态之间的时间改变量$ \Delta t $ ,通过式(1)可得出下一个时刻$ t $ 无人机的状态量:$$ \left\{ \begin{gathered} {v_t} = {v_0} + a \times \Delta t \\ \theta = \frac{{g\tan \varphi }}{{{v_t}}} \\ {x_t} = {x_0} + v\cos \theta \times \Delta t \\ {y_t} = {y_0} + v\sin \theta \times \Delta t\begin{array}{*{20}{c}} {} \\ {} \end{array} \\ {z_t} = {z_0} + \Delta h \times \Delta t \\ \end{gathered} \right. $$ (1) 式中,
${v_t}$ 表示无人机在时刻$t$ 的速度;$g $ 为重力常量;$\theta $ 表示无人机在时刻$t$ 的航向角,由杜宾斯运动学方程得出;$ {x}_{t},{y}_{t},{z}_{t} $ 为无人机在$ t $ 时刻的坐标。根据技术标准[21],本文为无人机运动模型定义下列性能约束条件,如表1所示。
表 1 飞行性能约束条件参数 取值范围 飞行速度$ v/{\mathrm{m \cdot s}}^{-1} $ [10, 25] 无人机倾斜角$ \varphi $/(°) [−25, 25] 高度变化率$ \Delta h/{\mathrm{m \cdot s}}^{-1} $ {−2,0,2} 2. 避障问题求解
2.1 避障过程建模
无人机在自主飞行中的避障问题可总结为无人机观测周围空域环境获取环境信息,求解最优飞行决策,通过执行飞行动作接近目标点,然后更新自身位置、速度等状态信息,最后重复上述步骤直至到达目标点。这类避障行为属于序列决策过程,在强化学习理论当中,通常将这一过程表达为马尔可夫决策过程(Markov decision process, MDP)[24],其框架如图4所示。
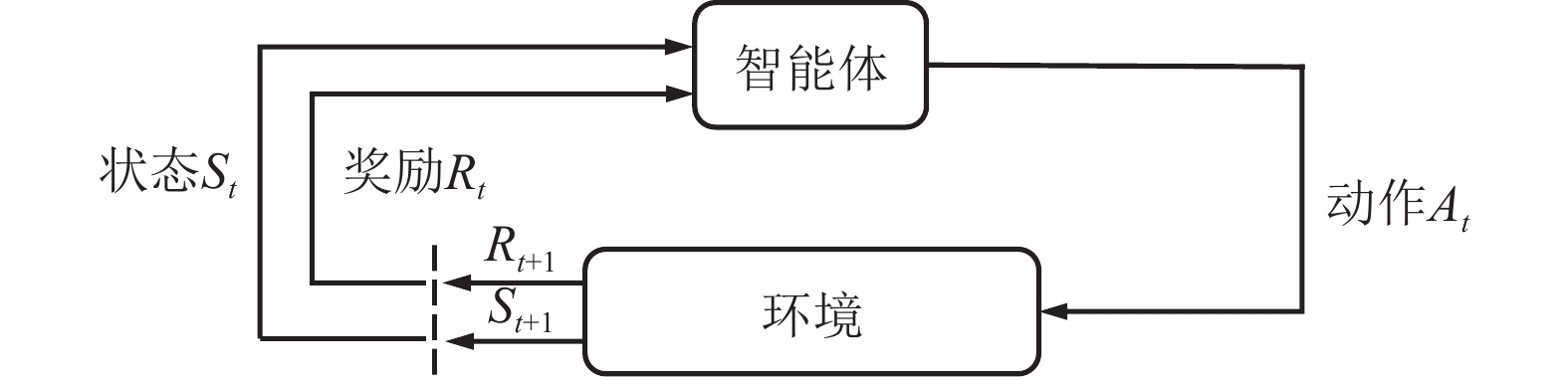
图4中St是一组有限状态集,表示无人机在避障过程中所经过的一系列状态集合,且下一个状态
$ {S}_{t+1} $ 与过去若干个状态$ S_0,S_1,\cdots,S_{t-1} $ 均无关,而只与当前状态$ {S}_{t} $ 有关,如式(2)所示;At是一组有限动作集,包含了无人机所有可执行的离散动作;Rt表示无人机通过执行动作集At中的一个动作,从当前状态$ {S}_{t} $ 转换到下一状态$ {S}_{t+1} $ 所获得的奖励。本文将奖励值Rt进行归一化处理表示为[0, 1]区间下的连续变量。$$ P\left({S}_{t+1}\left|{S}_{t}\right.\right)=P({S}_{t+1}\left|{S}_{0},{S}_{1},\cdots \right.,{S}_{t}) $$ (2) 下面将结合无人机运行特性对状态集、动作集以及奖励函数的设计进行解释。
2.1.1 无人机状态集设计
模型中无人机的状态由坐标位置、速度、航向角度、飞行高度4个分量表示;动态障碍的状态同样由坐标位置、速度、航向角度和高度4个分量表示;目标点的状态由坐标位置3个分量表示。设t时刻状态为
$ {S}_{t} $ ,若模型中有n架入侵机,那么状态$ {S}_{t} $ 将由(7+6n)维状态向量组成:$$ ({o_x},{o_y},{o_z},{o_v},{o_\theta }, \cdots ,i_x^{\left( k \right)},i_y^{\left( k \right)},i_z^{\left( k \right)},i_v^{\left( k \right)},i_\theta ^{\left( k \right)}, \cdots ,{g_x},{g_y},{g_z}) $$ (3) 式中,
$ {o_x},{o_y},{o_z} $ 为无人机的位置状态;$ {o_v} $ 为无人机的速度状态;$ o_{\theta} $ 为无人机的航向状态;$ i_x^{\left( k \right)},i_y^{\left( k \right)},i_z^{\left( k \right)} $ 为第k个入侵机的位置状态;$ i_{v}^{(k)} $ 为第k个入侵机的速度状态;$ i_{\theta}^{(k)} $ 为第k个入侵机的航向状态;$ g_{x}, g_{y}, g_{z} $ 为目标点的位置状态。2.1.2 无人机动作集合设计
为了提高算法求解效率,本文将模型中的动作空间进行离散化处理。因此无人机的动作集合
$ A $ 可由加速度动作子集$ {A_a} $ 、倾斜角动作子集$ {A_\varphi } $ 以及高度动作子集$ A_{h} $ 组成3×3×3维的有限集合表示:$$ A = \left\{ {{A_a},{A_\varphi },{A_h}} \right\} $$ (4) 考虑到无人机的飞行性能以及相关法规[23],上述3个动作子集取值范围如表2所示。
表 2 动作集合参数参数 值 加速度动作子集$ {A_a} $/m·s−2 $ \left\{ { - 5,0,5} \right\} $ 倾斜角动作子集${A_\varphi }$/(°) $\left\{ { - 5 ,0 ,5 } \right\}$ 高度动作子集${A_h}$/m·s−1 $ \left\{-2,\ 0, 2\right\}\ $ 无人机每次执行飞行动作前都会分别从加速度动作子集、倾斜角动作子集以及高度动作子集中通过算法解耦得到一个加速度和倾斜角以及高度改变作为最佳飞行动作
${a_{{\text{best}}}}$ :$$ {a_{{\text{best}}}} \in \left\{ {{a_a},{a_\varphi },\Delta h} \right\} $$ (5) 式中,
$ a_{a} $ 为加速度动作子集中的元素;${a_\varphi }$ 斜角动作子集中的元素;$\Delta h$ 为高度动作子集中的元素;{${a_a},{a_\varphi },\Delta h$ }代表由加速度和倾斜角以及高度改变构成的最优动作组合值。2.1.3 改进奖励估值函数
奖励函数是指在强化学习中,通过某种映射函数将状态和动作映射到一个奖励值,表示智能体对该状态和动作的收益或损失。奖励函数能够在每个时刻为智能体提供一个奖励,作为智能体在该时刻的反馈信号。智能体根据这个反馈信号调整自身策略选择最优的动作,从而获取最大化累积奖励值。
奖励函数的设计将直接影响到无人机的行为动作,奖励函数需要能够引导无人机执行设计者所期望的飞行动作(按照成本开销最小的方式避开障碍向目标点飞行),同时避免不希望的动作(发生空中冲突或相撞)。
本文中无人机执行飞行动作不断接近目标点是为了最大化自身所获得的累计奖励值。对于分层运行模式,除非进行避障,无人机不能主动改变高度,且在完成避障后通常需要回到原来的飞行高度,以免发生潜在的二次冲突。因此,需要根据这一实际运行情况对奖励函数
$ R(s) $ 进行优化设计。由2个稀疏奖励和1个密集奖励组成。
1)当无人机成功到达目标点则给予累计奖励值取1;
2)当无人机发生空中冲突则将受到最大惩罚,累计奖励值归零;
3)无人机在无碰撞的飞行过程中,不再适用于整数型的稀疏奖励值,需要通过密集的连续奖励值在每个时刻
$t$ 给予无人机反馈,使得无人机能够不断获取更大的奖励,迭代更新状态空间,采取更优飞行动作。对于3)这种情况下的奖励值,本文通过构建一个包含正值奖励和负值奖励的组合进行表达,其中正值奖励表示无人机在飞行过程中通过接近目标点所获得的收益,负值奖励表示无人机偏离初始高度所受到的惩罚。
具体而言,正值奖励
$ d(p) $ 用于反馈无人机与目标点的相对距离关系,并将其归一化表示为:$$ d(p) = \frac{{\max \left\{ {{d_{{\text{goal}}}}} \right\} - {d_{{\text{goal}}}}}}{{\max \left\{ {{d_{{\text{goal}}}}} \right\}}} $$ (6) 式中,
$ {d_{{\text{goal}}}} = \sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2}} $ 为无人机相对于目标点的欧式距离;$ \max \left\{ {{d_{{\text{goal}}}}} \right\} $ 表示无人机与目标点之间的最大距离,其值为常量,大小取决于不同的模型参数。因此,$ d(p) $ 表示无人机与目标点的相对距离越短所获得的奖励值就越大,且当相对距离足够小时,则有$ \mathop {\lim }\limits_{{d_{{\text{goal}}}} \to 0} \dfrac{{\max \left\{ {{d_{{\text{goal}}}}} \right\} - {d_{{\text{goal}}}}}}{{\max \left\{ {{d_{{\text{goal}}}}} \right\}}} = 1 $ 。负值奖励用于反馈无人机偏离初始飞行高度层的程度,表示如下:
$$ d(n) = - \left| {\frac{{{H_{{\text{crt}}}} - {H_0}}}{{{H_{\max }}}}} \right| $$ (7) 式中,
$ {H_{{\text{crt}}}} $ 代表无人机当前高度;$ {H_0} $ 表示设定的初始高度;$ {H_{\max }} $ 表示最大允许的高度改变量。无人机因改变高度而导致出现偏离,那么偏离量越大,奖励也将更大。$d(n)$ 用于引导无人机在避障的同时尽可能最小化飞行高度的偏离量,从而减少对其他高度层的干扰。综上所述,将本文中的奖励估值函数
$ R(s) $ 整合表达为:$$ R(s)=\left\{\begin{array}{ll}\text{1} & {d}_{\text{goal}} < 2且d\left(n\right)=0 \\ d(p)+\delta d\left(n\right) & {d}_{\text{goal}}\ge 2且{d}_{\text{uav}} > 10 \\ 0 & {d}_{\text{uav}}\le 10 \end{array}\right. $$ (8) 式中,
$ {d_{{\text{uav}}}} $ 为无人机与最近障碍之间的相对距离;$ \delta $ 为高度影响因子,用于调整高度变化对算法决策的影响程度。$\delta $ 值越大,无人机在发生冲突时越偏向于采取改变高度的避障方式;反之,无人机更倾向于选择改变方向避障。2.2 求解算法描述
求解马尔可夫决策过程需要找到一个策略
$ \pi $ ,这个策略是一个从状态S到动作A的映射,即在当前状态下对于动作的条件概率分布情况:$$ \pi (a|s) = P({A_t} = a|{S_t} = s) $$ (9) 策略
$ \pi $ 将影响着马尔可夫决策过程的求解结果,如果想要得到最优解,那么须找到一个最优策略$ \pi^{*} $ ,该策略能使得最终期望的总奖励值最大化,其表达式为:$$ {\pi ^*} = \mathop {\arg \max }\limits_\pi \mathbb{E}\left[ {\sum\limits_{t = 0}^T {{R_{st,at}}} \left| \pi \right.} \right] $$ (10) 式中,
$ R_{s t, a t} $ 代表在t时刻状态$ {S_t} $ 选取动作$ {a_t} $ 所获得的当前奖励值;$ \mathbb{E}\left[\displaystyle\sum_{t=0}^{T} R_{st,at} \mid \pi\right] $ 代表从初始时刻状态$ {S_0} $ 到终末状态$ {S_T} $ 在策略$ \pi $ 下所获得的奖励值的期望。本文采用的最优策略求解算法是蒙特卡罗树搜索(Monte Carlo tree search, MCTS),在搜索过程中,利用搜索树上限置信区间算法(upper confidence bound apply to tree, UCT)来寻找一个最佳的策略对树进行搜索,通过各个节点的UCT值来决定访问哪一个节点。UCT算法如下:
$$ {\mathrm{UCT}} = {Q(v')/{N(v')}} + C\sqrt{{2\ln N(v)}/{N(v')}} $$ (11) 式中,
$ v $ 表示当前节点;$ v^{\prime} $ 表示当前节点的子节点;$ Q $ 表示节点的总奖励值;$ N $ 表示节点被访问的次数;${{Q(v')}}/{{N(v')}}$ 表示这个子节点的平均奖励值;$\sqrt{{2\ln N(v)}/{N(v')}}$ 表示该父节点的总访问次数与其子节点的访问次数的比值;$ C $ 是一个常量参数,它可以调整比值的权重,根据文献[25]中提出的经验值,取$ C = {1/{\sqrt 2 }}$ 。2.3 算法参数调整优化
上文中已经确立奖励估值函数的表达式,但式(8)中的高度影响因子
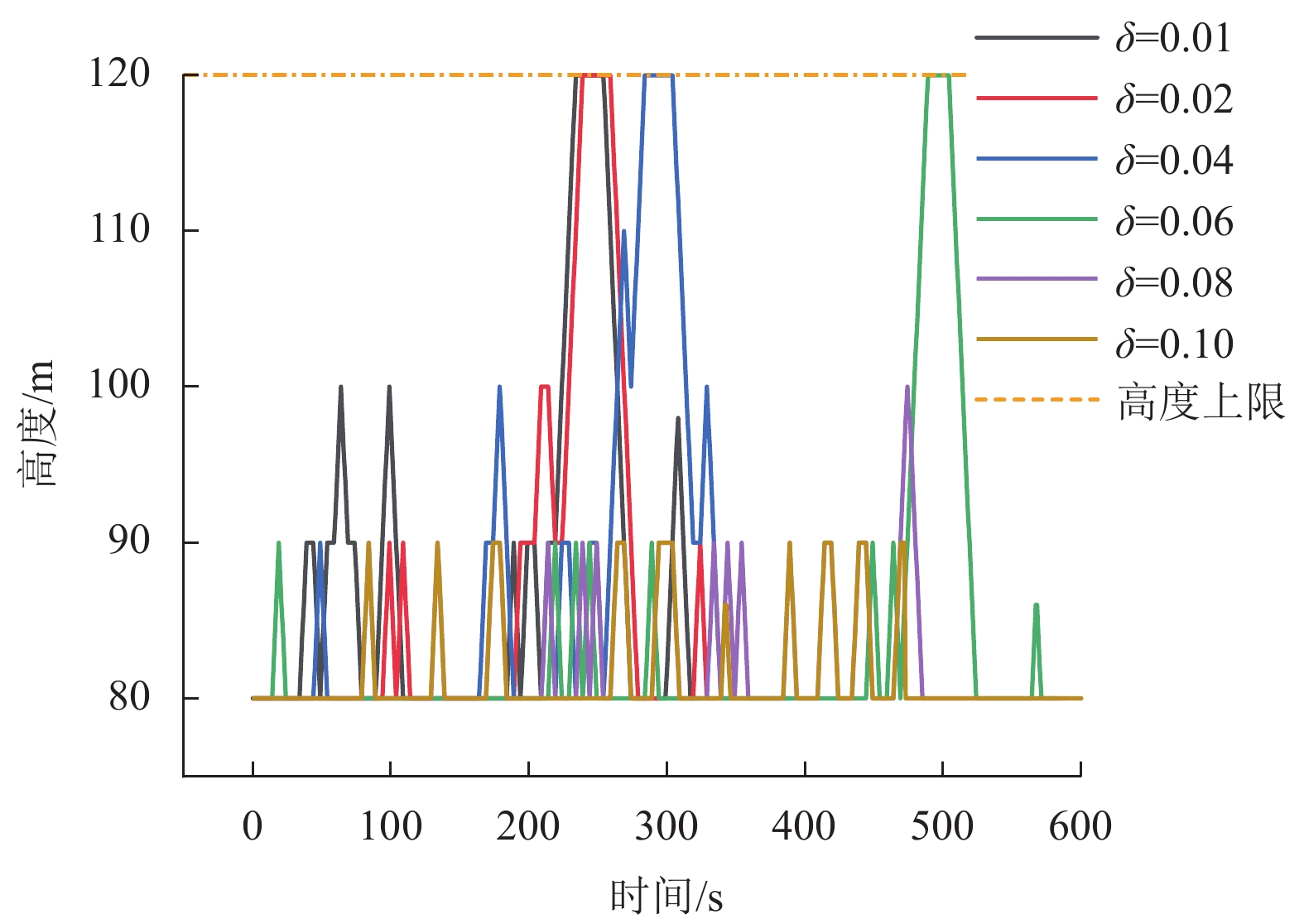
$ \delta $ 的最优值暂未确定,因此需要确定一个最优参数。由于无人机在巡航阶段需要尽可能保持所在飞行高度层,非必要情况下尽量不通过改变高度来避障,对于改变飞行高度的避障策略优先级较低。因此,高度影响因子$ \delta $ 需要设定为一个较小的数值,即高度改变的优先度较低。通过对不同的高度影响因子
$ \delta $ 进行仿真,得到图5所示结果。当高度影响因子$ \delta $ 较大时,会造成算法通过改变飞行高度所获得的奖励值偏小,因此算法将倾向于保持当前飞行高度,但这样会使得无人机无法利用冗余性能对障碍物进行超越。若高度影响因子$ \delta $ 设置过于小,则会造成无人机高度偏离过多,容易干扰到其他高度层的交通流从而影响整个空域系统的稳定。综合飞行时间以及飞行稳定性,选取$\delta = 0.02$ ,采用该系数的算法偏离程度更小且对于障碍能够在较短的时间内进行快速反应,减少了飞行时间。3. 数值仿真与分析
3.1 三维避障仿真
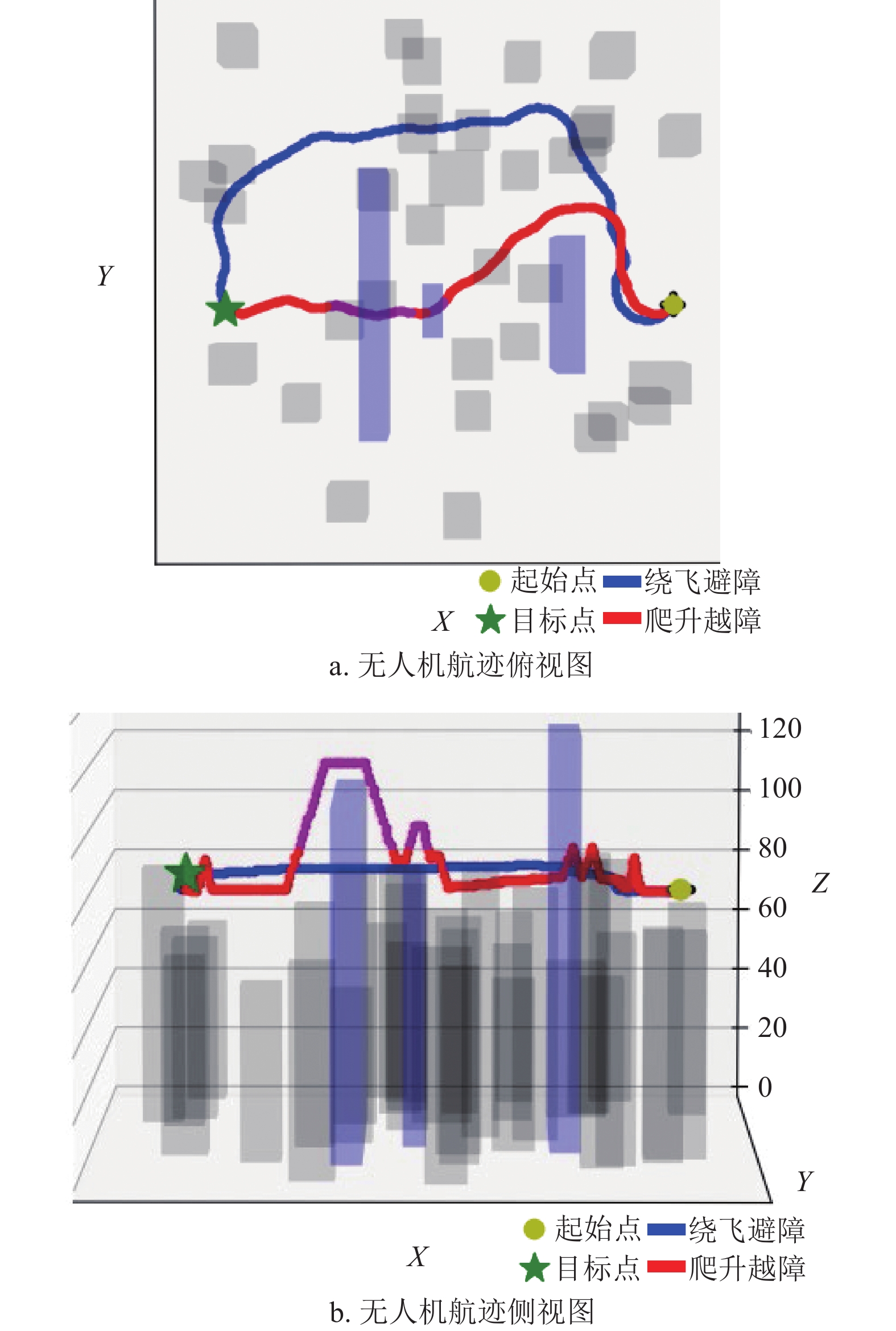
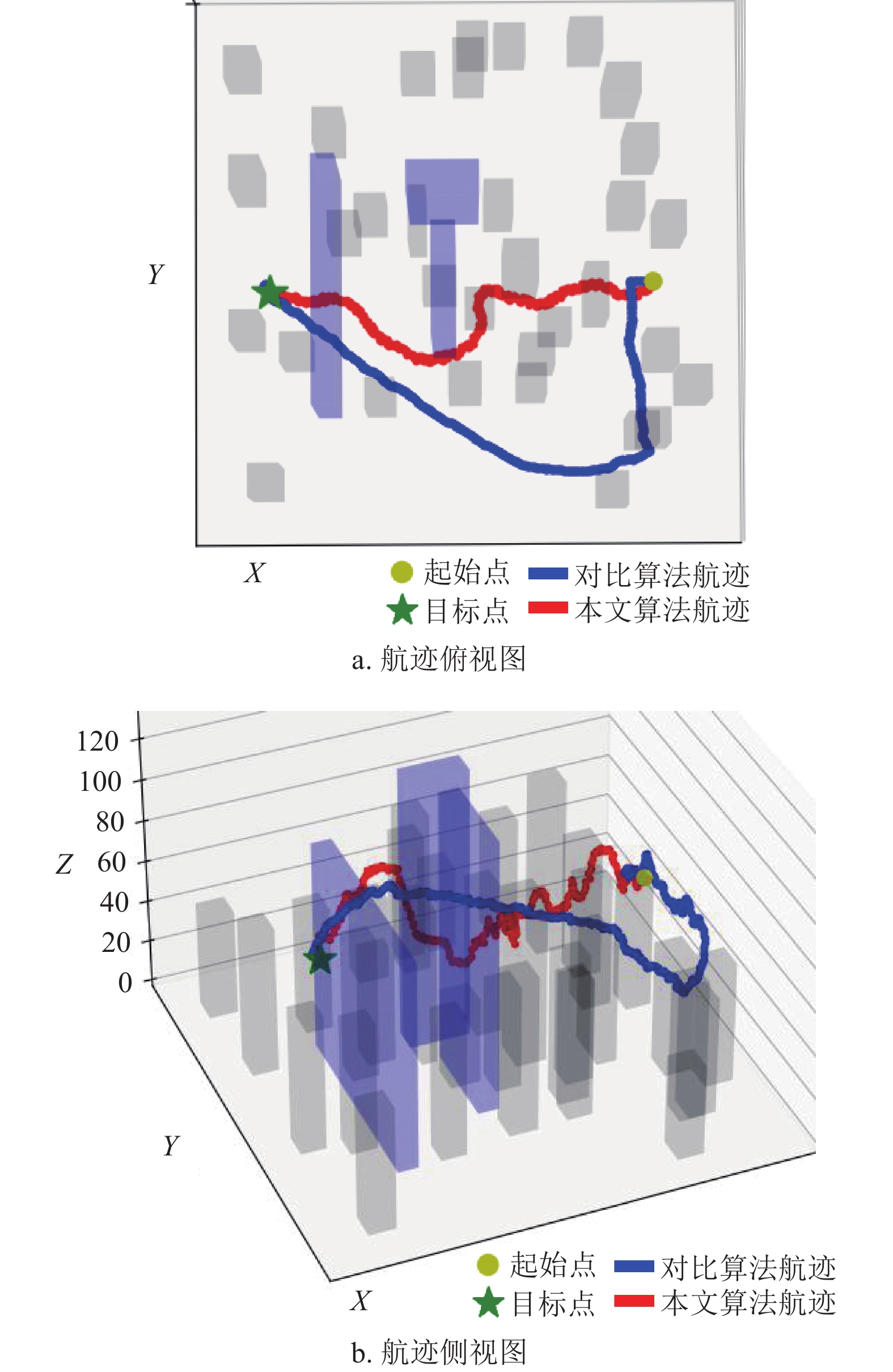
在城区飞行只要真高达到80 m便可以超越大多数静态障碍,因此仿真中设定无人机初始飞行高度为80 m。仿真界面如图6,黄色圆形图标为无人机的起始点,绿色五角星图标为目标点,无人机从黄色起始点到达绿色目标点的飞行过程中,需要对障碍物在垂直高度上保持至少10 m的距离冗余。
本文采取100组重复随机仿真来减小实验误差,每组实验中的静态障碍物几何外形和位置固定,入侵机位置和初始速度随机,目标点和无人机起始点坐标随机,最后取100组实验数据的算术平均值作为仿真结果。仿真基于Python 3.7,CPU为AMD Ryzen 74 800U,内存为16 GB。
选取其中一组仿真中的无人机航迹来进行说明,如图6所示。图6中蓝色线条代表的是仅采取在初始飞行高度上进行绕飞避障策略的无人机典型航迹;图中红色线条代表的是可以通过改变高度对障碍物进行超越或者进行绕飞的避障策略的无人机典型航迹。从图中可以看出,当面对第一个蓝色障碍时,由于障碍物高度较高而宽度相对较短,无人机都选择了进行绕飞,因此两种避障策略下的飞行航迹基本一致。当面对第二个蓝色障碍时,由于障碍物的高度相对较低,红色航迹的无人机选择了进行爬升越障的策略以尽早到达目标点;而蓝色航迹的无人机由于选择绕飞的策略从而耗费了更多时间。
最终仿真的结果如表3所示,对于采取绕飞及越障的避障策略,虽然飞行均速较慢,但其飞行时间缩短了24.4%、航迹长度减少了33.2%,从而提高运行效率并降低了飞行能耗,因此更适合城市低空下的轻小无人机。
表 3 不同避障策略下的仿真结果对比算法策略 飞行时间/s 航迹长度/km 飞行均速/m·s−1 仅允许绕飞 356 7.3 20 绕飞及越障 269 4.87 18 3.2 算法鲁棒性分析
城市密集建筑物和地形障碍的遮挡容易导致无人机感知系统出现盲区,从而造成环境状态不完全可观测。无法获取足够的状态信息用于求解,造成算法性能下降,因此对避障算法在感知系统受限下的鲁棒性提出了要求。
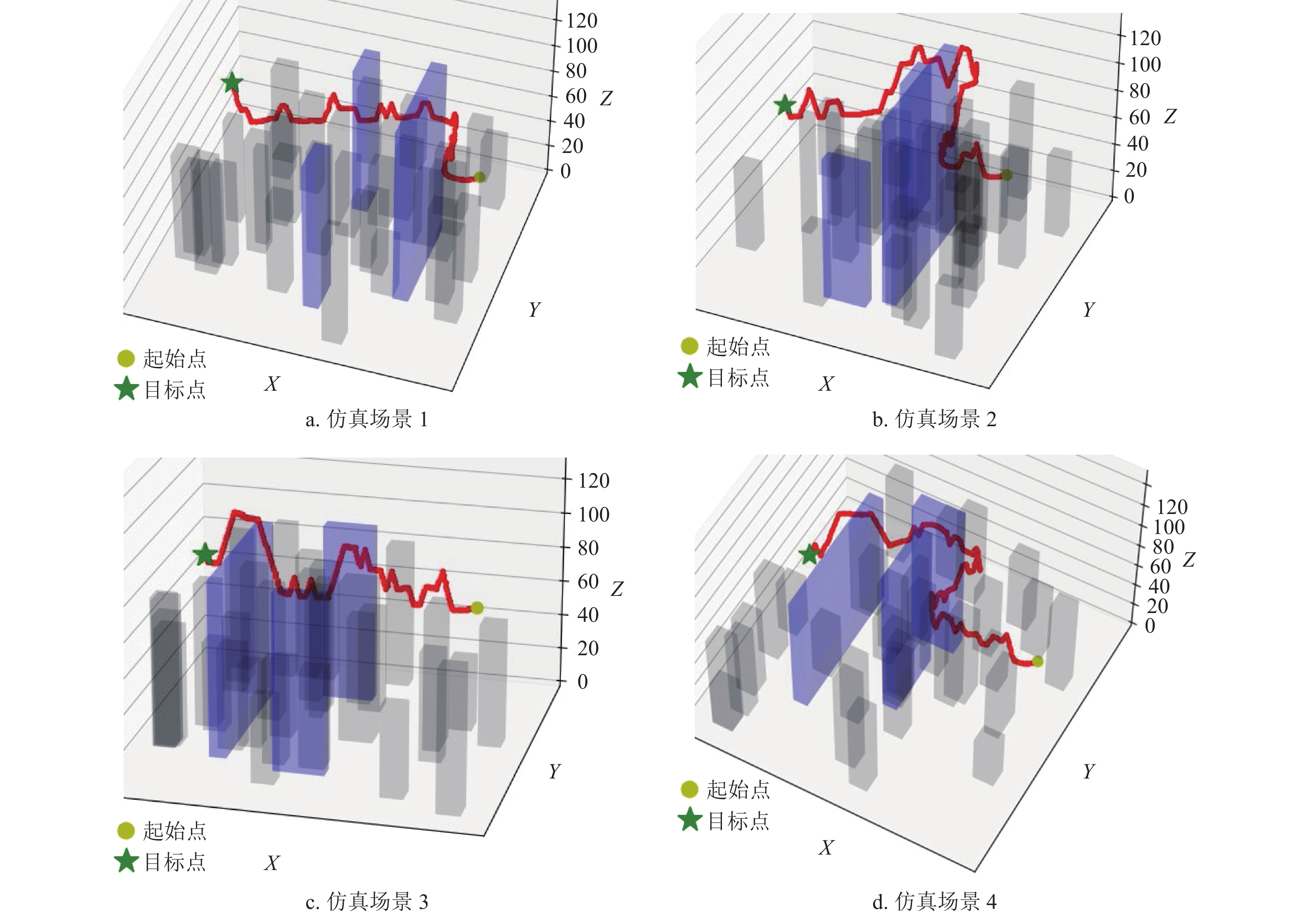
对于本项仿真实验,设计了多组重复随机仿真场景,仿真模型中静态障碍物的数量、位置、几何外形皆为随机改变(如图7所示),以此验证避障算法在不同感知范围半径下的性能表现,即限制试验机能够获取到外部环境信息的最大距离。
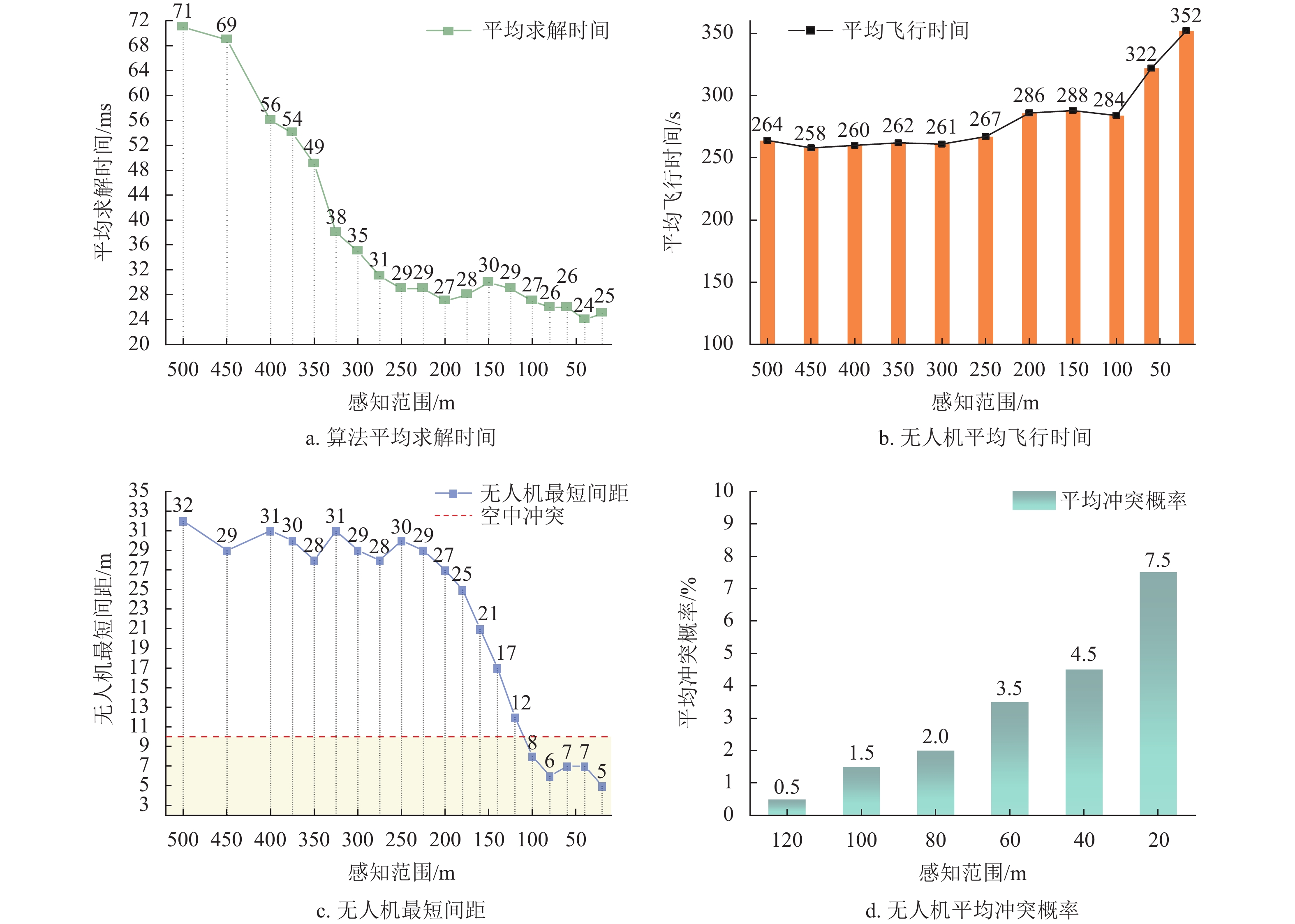
目前轻小型无人机所搭载的激光雷达探测范围大多在500 m以内,因此本项仿真以500 m为初始半径开始逐步缩小感知范围直到半径等于20 m,最终仿真结果如组图8所示。仿真中由于感知半径小于120 m后才会出现空中冲突的情况,因此图8d中的横坐标初始刻度为120 m。
由图8a可知,算法的求解时间从感知半径500~250 m内,由于输入信息量减少,算法效率得到小幅度提高,说明该算法在处理大量数据时性能没有下降;当半径小于250 m,求解时间基本保持不变,算法整体性能未出现明显波动。由图8b可知,对于无人机的平均飞行时间,当感知半径小于225 m,由于环境状态信息输入大量减少,从而导致部分环境状态数据缺失,因此算法对于全局最优解的计算能力出现下降,平均飞行时间增加。由图8c可知,对于无人机的最小间距,当感知半径小于200 m时,无人机的最小间距开始出现明显下降;当感知半径小于120 m,算法无法再保证足够的间隔距离,开始出现空中冲突。由图8d可知,随着感知半径缩短,冲突概率出现了上升。
3.3 算法对比实验
快速扩展随机树算法(rapidly exploring random tree, RRT)是用于运动体避障的高效算法[26-27],具有求解迅速的特点。将本文算法与RRT的动态求解算法Dynamic-RRT[28]进行比较,Dynamic-RRT算法能够充分利用建立完成的搜索树信息在环境出现变化时通过剪枝并重新生长的方式快速构建新的搜索树,因而能针对动态变化的环境进行实时求解。
根据图9中仿真实验的航迹对比结果,Dynamic-RRT算法在避障过程更容易偏离设定的飞行高度,从而干扰空域内的其他飞行器,无法得到理想的飞行航迹。从表4的实验数据可以发现,相较于Dynamic-RRT,本文算法能够得到更短的飞行航迹,飞往目标点所消耗的时间也更少,空中发生冲突的概率更低,具有良好的求解质量。表4中“单次求解时间”定义为飞行过程中计算避障动作的时间开销。本文算法相较于Dynamic-RRT,虽然计算时间稍长,但是并没有对避障产生影响,求解效率仍然在可接受范围以内,能够保证算法的整体实时性。
表 4 算法对比结果实验数据 本文算法 Dynamic-RRT 航迹长度/km 5.38 7.90 飞行时间/s 278 439 冲突概率/% 2 8 单次求解时间/ms 21 17 4. 结束语
本文针对城市低空运行环境的特点以及无人机性能约束构建了仿真模型,将无人机避障问题表达为马尔可夫决策过程并通过蒙特卡罗树搜索求解。通过将无人机动作集拓展到三维空间,实现了无人机绕飞和越障的避障策略;其次通过改进奖励估值函数并优化参数,使得算法能够自主决策选择更优的避障动作,缩短无人机飞行时间,加速城市空中交通高效流动;最后通过在仿真中限制无人机的感知范围使其处于不完全可观测的环境中,以此验证无人机在感知系统受限条件下的鲁棒性。仿真结果表明本文算法仍然能够给出完整的可行解,从而较大程度地降低空中冲突概率,保证了城市场景运行的安全。
-
表 1 飞行性能约束条件
参数 取值范围 飞行速度$ v/{\mathrm{m \cdot s}}^{-1} $ [10, 25] 无人机倾斜角$ \varphi $/(°) [−25, 25] 高度变化率$ \Delta h/{\mathrm{m \cdot s}}^{-1} $ {−2,0,2} 表 2 动作集合参数
参数 值 加速度动作子集$ {A_a} $/m·s−2 $ \left\{ { - 5,0,5} \right\} $ 倾斜角动作子集${A_\varphi }$/(°) $\left\{ { - 5 ,0 ,5 } \right\}$ 高度动作子集${A_h}$/m·s−1 $ \left\{-2,\ 0, 2\right\}\ $ 表 3 不同避障策略下的仿真结果对比
算法策略 飞行时间/s 航迹长度/km 飞行均速/m·s−1 仅允许绕飞 356 7.3 20 绕飞及越障 269 4.87 18 表 4 算法对比结果
实验数据 本文算法 Dynamic-RRT 航迹长度/km 5.38 7.90 飞行时间/s 278 439 冲突概率/% 2 8 单次求解时间/ms 21 17 -
[1] 樊邦奎, 李云, 张瑞雨. 浅析低空智联网与无人机产业应用[J]. 地理科学进展, 2021, 40(9): 1441-1450. DOI: 10.18306/dlkxjz.2021.09.001 FAN B K, LI Y, ZHANG R Y. Initial analysis of low-altitude Internet of intelligences(IOI) and the applications of unmanned aerial vehicle industry[J]. Progress in Geography, 2021, 40(9): 1441-1450. DOI: 10.18306/dlkxjz.2021.09.001
[2] 中国民用航空局. 民用无人驾驶航空发展路线图V1.0(征求意见稿) [EB/OL]. [2023-08-30]. http://www.caac.gov.cn/ig5/www.caac.gov.cn/PHONE/HDJL/YJZJ/202208/P020220822615871900321.pdf. Civil Aviation Administration of China. Civil unmanned aerial vehicle development roadmap V1.0 (Exposure draft) [EB/OL]. [2023-08-30]. http://www.caac.gov.cn/ig5/www.caac.gov.cn/PHONE/HDJL/YJZJ/202208/P020220822615871900321.pdf.
[3] 中华人民共和国交通运输部. 无人机物流配送运行要求: JT/T 1440—2022[S]. 北京: 人民交通出版社. Ministry of Transport of the People's Republic of China. Operation requirements for unmanned aircraft logistics distribution: JT/T 1440—2022[S]. Beijing: China Communications Press.
[4] CHAKRAVARTHY A, GHOSE D. Obstacle avoidance in a dynamic environment: A collision cone approach[J]. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 1998, 28(5): 562-574. DOI: 10.1109/3468.709600
[5] LIN Z J, CASTANO L, MORTIMER E, et al. Fast 3D collision avoidance algorithm for fixed wing UAS[J]. Journal of Intelligent & Robotic Systems, 2020, 97(3): 577-604.
[6] TAO J W, JI W C, FAN Q J. An effective approach of collision avoidance for UAV[J]. Journal of Intelligent & Robotic Systems, 2023, 108(2): 18.
[7] FIORINI P, SHILLER Z. Motion planning in dynamic environments using velocity obstacles[J]. The International Journal of Robotics Research, 1998, 17(7): 760-772. DOI: 10.1177/027836499801700706
[8] DOUTHWAITE J A, ZHAO S Y, MIHAYLOVA L S. Velocity obstacle approaches for multi-agent collision avoidance[J]. Unmanned Systems, 2019, 7(1): 55-64. DOI: 10.1142/S2301385019400065
[9] TAN C Y, HUANG S N, TAN K K, et al. Three dimensional collision avoidance for multi unmanned aerial vehicles using velocity obstacle[J]. Journal of Intelligent & Robotic Systems, 2020, 97(1): 227-248.
[10] LAVALLE S M, KUFFNER J J. Randomized kinodynamic planning[C]//Proceedings of the 1999 IEEE International Conference on Robotics and Automation. New York: IEEE, 1999: 473-479.
[11] MECHALI O, XU L M, WEI M Z, et al. A rectified RRT* with efficient obstacles avoidance method for UAV in 3D environment[C]//Proceedings of the IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems. New York: IEEE, 2019: 480-485.
[12] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90-98. DOI: 10.1177/027836498600500106
[13] 高扬, 陈靖淞, 郭钒, 等. 支线机场大型固定翼无人机冲突解脱方法研究[J]. 安全与环境学报, 2023, 23(9): 3143-3149. GAO Y, CHEN J S, GUO F, et al. Research on conflict resolution method of large fixed-wing UAV in regional airport[J]. Journal of Safety and Environment, 2023, 23(9): 3143-3149.
[14] JULIAN K D, KOCHENDERFER M J, OWEN M P. Deep neural network compression for aircraft collision avoidance systems[J]. Journal of Guidance Control Dynamics, 2019, 42(3): 598-608. DOI: 10.2514/1.G003724
[15] 陈正茂, 刘洪, 林毅. 基于深度高斯过程的飞行冲突探测方法研究[J]. 电子科技大学学报, 2021, 50(2): 261-266. DOI: 10.12178/1001-0548.2019191 CHEN Z M, LIU H, LIN Y. Study on algorithm for flight conflict detection basedon deep gaussian process[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(2): 261-266. DOI: 10.12178/1001-0548.2019191
[16] CHEN P Z, PEI J A, LU W Q, et al. A deep reinforcement learning based method for real-time path planning and dynamic obstacle avoidance[J]. Neurocomputing, 2022, 497: 64-75. DOI: 10.1016/j.neucom.2022.05.006
[17] ZHANG Q R, PAN W, REPPA V. Model-reference reinforcement learning for collision-free tracking control of autonomous surface vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(7): 8770-8781. DOI: 10.1109/TITS.2021.3086033
[18] 吕超, 李慕宸, 欧家骏. 基于分层深度强化学习的无人机混合路径规划[J]. 北京航空航天大学学报, 2023, DOI: 10.13700/j.bh.1001-5965.2023.0550. LYU C, LI M C, OU J J. UAV hybrid path planning based on hierarchical deep reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, DOI: 10.13700/j.bh.1001-5965.2023.0550.
[19] HOEKSTRA J M , ELLERBROEK J , SUNIL E , et al. Geovectoring: Reducing traffic complexity to increase the capacity of UAV airspace[EB/OL]. [2023-11-21]. https://www.researchgate.net/publication/326326818.
[20] NASA. Concepts of Airspace Structures and System Analysis for UAS Traffic flows for Urban Areas [EB/OL]. [2023-11-21]. https://www.nasa.gov/aeroresearch/utm-tech-docs-papers-presentations.
[21] 中国民用航空局. 城市场景轻小型无人驾驶航空器物流航线划设规范: MH/T 4054—2022[S]. 北京: 中国民航出版社. Civil Aviation Administration of China. Route design specification of the light-small unmanned aircraft system for urban logistics: MH/T 4054—2022[S]. Beijing: China Civil Aviation Publishing House.
[22] BALAKRISHNAN K, POLASTRE J, MOOBERRY J, et al. Blueprint for the sky. The roadmap for the safe integration of autonomous aircraft[R]. Santa Clara Valley: Airbus A3, 2018.
[23] 中国民用航空局. 城市场景物流电动多旋翼无人驾驶航空器: MH/T 6126—2022[S]. 北京: 中国民航出版社. Civil Aviation Administration of China. Technical requirements of multi-rotor electric unmanned aircraft system (small and light)for urban logistics: MH/T 6126—2022[S]. Beijing: China Civil Aviation Publishing House.
[24] BELLMAN R. A Markovian decision process[J]. Journal of Mathematics and Mechanics. 1957, 6(4): 679-684.
[25] LENTILHAC S. UAV flight plan optimzed for sensor requirements[C]//Proceedings of the IEEE Aerospace and Electronic Systems Magazine. New York: IEEE, 2010: 11-14.
[26] YUAN C R, LIU G F, ZHANG W Q, et al. An efficient RRT cache method in dynamic environments for path planning[J]. Robotics and Autonomous Systems, 2020, 131: 103595. DOI: 10.1016/j.robot.2020.103595
[27] QI J, YANG H, SUN H X. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 7244-7251. DOI: 10.1109/TIE.2020.2998740
[28] ZHAO P L, CHANG Y H, WU W K, et al. Dynamic RRT: Fast feasible path planning in randomly distributed obstacle environments[J]. Journal of Intelligent & Robotic Systems, 2023, 107(4): 48.

 ISSN
ISSN 


 下载:
下载: