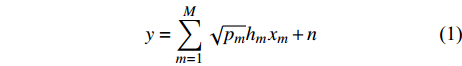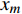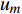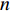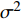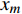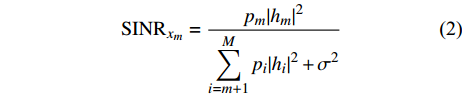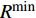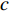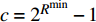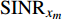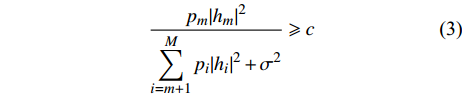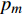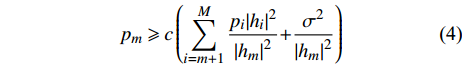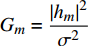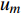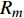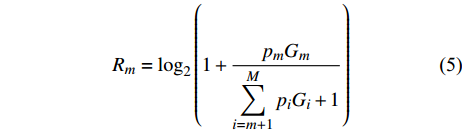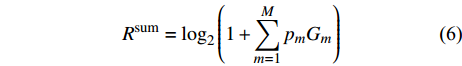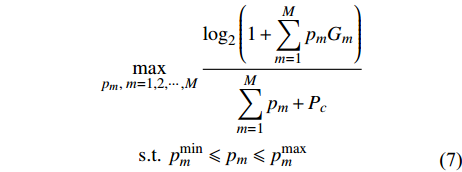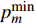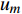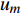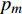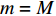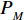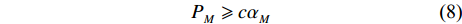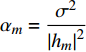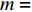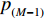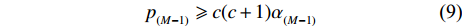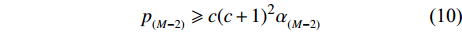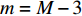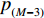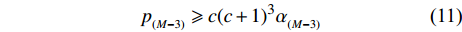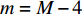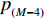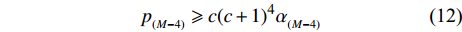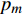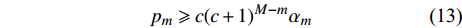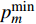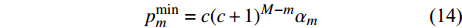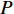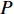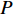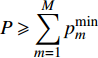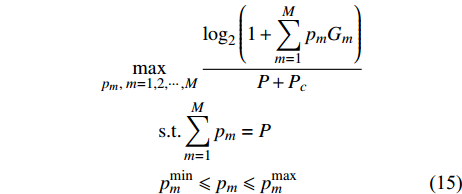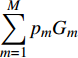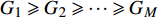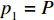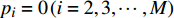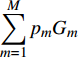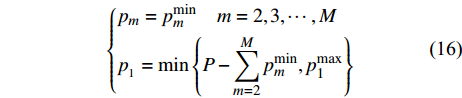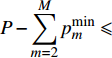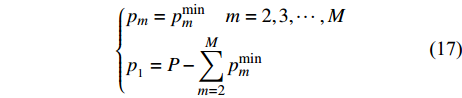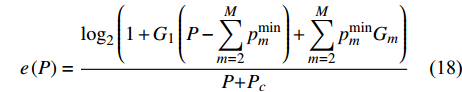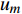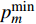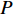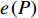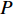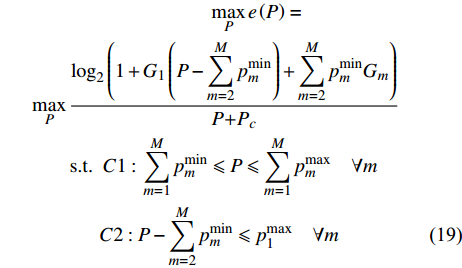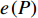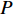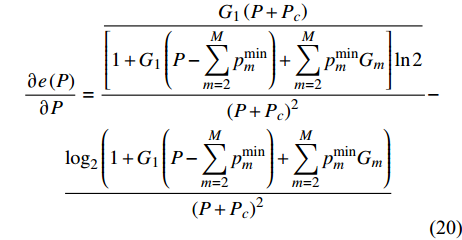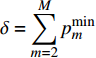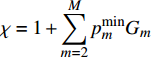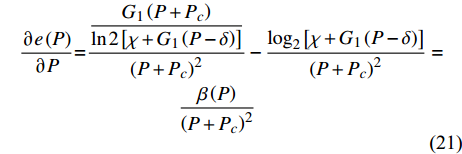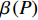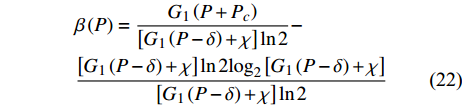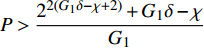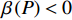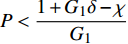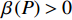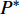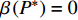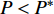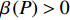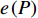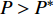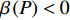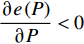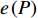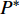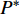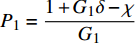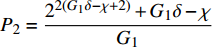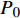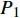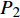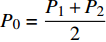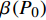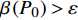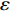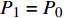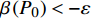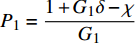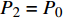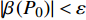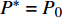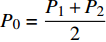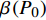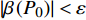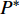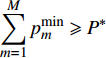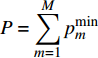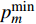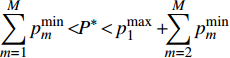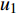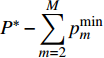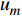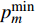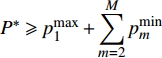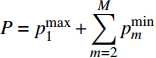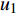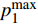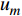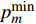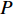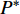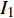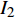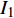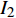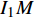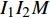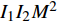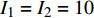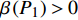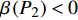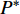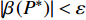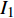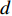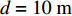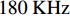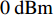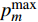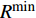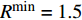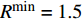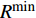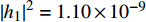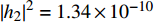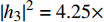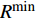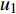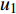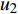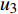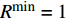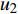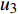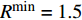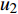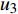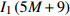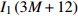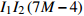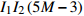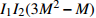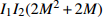Power Allocation with Maximizing Energy Efficiency for NOMA System
-
摘要: 已有的上行非正交多址接入(NOMA)系统中最大化能量效率的功率分配方案的计算量有待降低,针对此问题,该文提出了上行NOMA系统中低复杂度的最大化系统能量效率的功率分配方案。首先,根据用户的最低速率需求计算每个用户所需的最低功率,以单个用户的最大发送功率和用户的最低速率需求作为约束条件,建立最大化能量效率的功率分配优化问题,然后求解所有用户的总功率为常数时最大的能量效率及其对应的功率分配,最后求解总功率变化时最大化能量效率的功率分配。仿真结果显示,随着信噪比的变化,该文所提方案的系统能量效率高于或等于相同场景中的已有方案。Abstract: The computational amount of the existing power allocation scheme to maximize energy efficiency for uplink non-orthogonal multiple access (NOMA) systems needs to be reduced. To solve this problem, low complexity power allocation scheme to maximize the energy efficiency is proposed for uplink NOMA system. Firstly, the minimum power required by each user is calculated according to the minimum rate requirement of the users, the power allocation optimization problem for maximizing energy efficiency is established with the constraints of the maximum transmission power and the minimum rate requirement of the users. Then, maximum energy efficiency and its corresponding power allocation are obtained with the powers of all users as a constant. Finally, the solution of power allocation to maximize energy efficiency is solved with variable total power. Simulation results show that the energy efficiency of the proposed scheme is higher than or equal to that of the existing schemes in the same scene with the change of signal-to-noise ratio.
-
非正交多址接入NOMA技术是第五代移动通信系统的关键技术之一[1]。NOMA的思想是:在同一个无线资源块上同时为多个用户服务,接收端采用连续干扰消除技术消减用户之间的干扰[2]。因此,支持更多用户连接和更高频谱效率的NOMA技术成为产业界和学术界的研究重点[3]。
NOMA中的功率分配关系到系统的性能[4-5]。文献[6-11]研究了下行NOMA系统中最大化和速率以及能量效率(energy efficiency, EE)的功率分配。对于包含任意用户的单簇NOMA系统,文献[6]提出了一种最大化和速率的功率分配方案。对于多簇且每个簇包含两用户NOMA系统,文献[7]给出了一种基于迭代的最大化和速率的功率分配方案。文献[8]将文献[7]中的场景扩展到每个簇包含任意用户的NOMA系统,在用户最大发送功率和每个簇中用户的最大数目约束下,提出了最大化系统权重和速率的功率分配方案。文献[9]以总功率和用户最低速率需求作为约束条件,提出了单簇NOMA系统中最大化EE的功率分配方案。对于多簇且每个簇分别包含两用户和任意用户的NOMA系统,文献[10]和文献[11]分别提出了最大化EE的功率分配方案。
文献[12-14]研究了上行NOMA系统中最大化和速率的功率分配方案。对于包含两用户的上行单簇NOMA系统,文献[12]以单个用户最大发送功率作为约束条件,利用图论中的最大加权独立集方法求解了最大化系统和速率的功率分配。文献[13]给出了多簇且每个簇包含两用户的上行NOMA系统中最大化和速率的功率分配方案。文献[14]将文献[13]中的场景扩展到每个簇包含任意用户的上行多簇NOMA系统,采用注水和几何规划两种算法求解了最大化系统和速率的功率分配。然而,文献[12-14]没有考虑到用户的权重。对于多簇且每个簇包含两用户的NOMA系统,文献[15]推导了最大化系统权重和速率的功率分配方案。
最大化EE是上行NOMA系统中功率分配方案的目标之一[16-17]。文献[18]以单个用户的最大发送功率和单个用户的最低速率需求作为约束条件,提出了上行单簇NOMA系统中最大化EE的功率分配方法。文献[19]建立了多簇且每个簇包含任意用户的上行NOMA系统中最大化系统EE的功率分配优化问题,并利用丁克尔巴赫算法求解该问题。对于多簇且每个簇包含任意用户的上行NOMA系统,文献[20]以用户的最大发送功率作为约束条件,给出了基于注水算法的最大化EE的功率分配方案。然而文献[19-20]的计算量有待于降低。
针对文献[19-20]的不足,本文提出了包含任意用户的上行NOMA系统中低复杂度的最大化EE的功率分配方案。以单个用户的最大发送功率和用户的最低速率需求作为约束条件,建立最大化EE的功率分配优化问题,求解该优化问题,得到最大化EE的功率分配。仿真结果显示,随着信噪比的变化,所提方案的系统EE高于或等于相同场景中的已有方案。
1. 系统模型
如图1所示,考虑包含1个基站和M个用户的单小区上行NOMA系统,基站和用户都配置单根天线。用
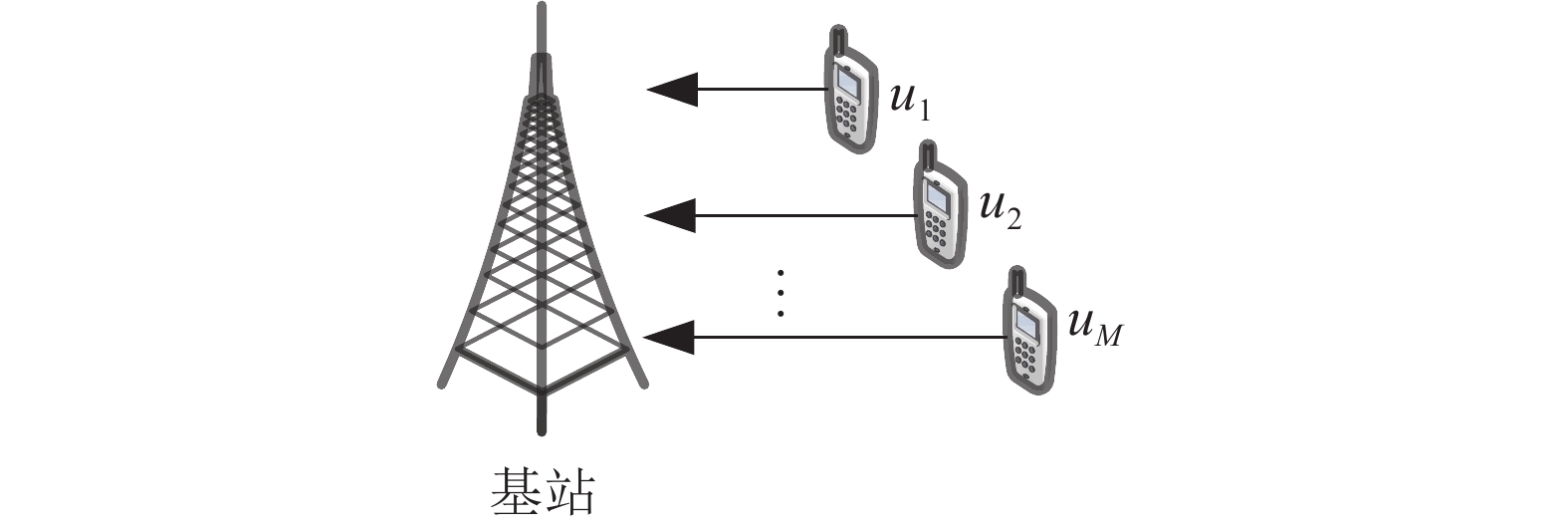
${u_m}$ 表示第m个用户,m=1, 2, ··· , M。所有用户使用相同的频段,${u_m}$ 到基站的信道为${h_m}$ ,${\left| {{h_{\rm{1}}}} \right|^2} \geqslant {\left| {{h_2}} \right|^2} \geqslant \cdots \geqslant {\left| {{h_M}} \right|^2}$ 。${u_m}$ 的发送功率为${p_m}$ ,$p_m^{\max }$ 是用户${u_m}$ 最大的发送功率。用
$y$ 表示基站的接收信号,$y$ 的表达形式为:$$y = \sum\limits_{m = 1}^M {\sqrt {{p_m}} {h_m}{x_m}} + n$$ (1) 式中,
${x_m}$ 是${u_m}$ 的发送信号;$n$ 是基站接收到的高斯白噪声,均值为零,方差为${\sigma ^2}$ 。基站接收到的M个用户的信号相互干扰。采用与文献[15]相同的检测方法,基站先检测信道最优的用户的发送信号并消减该信号造成的干扰,然后从未检测的用户信号中选出信道最优的用户,检测该用户的发送信号并消减该信号造成的干扰,重复该过程直至检测出所有用户的信号。基站检测
${x_m}$ 时的信干噪比(signal to interference and noise ratio, SINR)为:$$ {\rm{SIN}}{{\rm{R}}_{{x_m}}} = \frac{{{p_m}{{\left| {{h_m}} \right|}^2}}}{{\displaystyle\sum\limits_{i = m + 1}^M {{p_i}{{\left| {{h_i}} \right|}^2}} + {\sigma ^2}}} $$ (2) 假定单个用户的最低单位带宽速率需求为
$R_{}^{\min }$ ,该速率对应的SINR为$c$ ,$c = {2^{R_{}^{\min }}} - 1$ ,${\rm{SIN}}{{\rm{R}}_{{x_m}}}$ 要满足:$$ \frac{{{p_m}{{\left| {{h_m}} \right|}^2}}}{{\displaystyle\sum\limits_{i = m + 1}^M {{p_i}{{\left| {{h_i}} \right|}^2}} + {\sigma ^2}}} \geqslant c $$ (3) 由此可推出,
${p_m}$ 的取值满足:$${p_m} \geqslant c\left( {\sum\limits_{i = m + 1}^M {\frac{{{p_i}{{\left| {{h_i}} \right|}^2}}}{{{{\left| {{h_m}} \right|}^2}}}} {\rm{ + }}\frac{{{\sigma ^2}}}{{{{\left| {{h_m}} \right|}^2}}}} \right)$$ (4) 令
${G_m} = \dfrac{{{{\left| {{h_m}} \right|}^2}}}{{{\sigma ^2}}}$ ,m=1, 2 , ··· , M,则${u_m}$ 的单位带宽速率${R_m}$ 的表达形式为:$$ {R_m} = {\log _2}\left( {1 + \frac{{{p_m}{G_m}}}{{\displaystyle\sum\limits_{i = m + 1}^M {{p_i}{G_i}} + 1}}} \right) $$ (5) 根据文献[15],M个用户的单位带宽和速率为:
$${R^{{\rm{sum}}}} = {\log _2}\left( {1 + \sum\limits_{m = 1}^M {{p_m}{G_m}} } \right)$$ (6) 所提方案的目标是:在满足每个用户最低单位带宽速率需求下,通过分配适当的功率,最大化系统的EE。功率分配的目标表示为:
$$ \begin{split} & \mathop {\max }\limits_{{p_m},\;m = 1,2, \cdots ,M} \frac{{{{\log }_2}\left( {1 + \displaystyle\sum\limits_{m = 1}^M {{p_m}{G_m}} } \right)}}{{\displaystyle\sum\limits_{m = 1}^M {{p_m}} + {P_c}}} \\ &\qquad {\rm{s.t.}}\;\,{\rm{ }}p_m^{\min } \leqslant {p_m} \leqslant p_m^{\max } \\ \end{split} $$ (7) 式中,
${P_c}$ 是所有用户消耗的电路功率,是一个常数;$p_m^{\min }$ 表示满足${u_m}$ 的最低单位带宽速率需求时${u_m}$ 所需的最低功率。2. 功率分配方案
本节首先推导了满足所有用户最低单位带宽速率需求时单个用户所需的最低功率,然后给出最大化系统EE的功率分配方案。
2.1 单用户最低功率的推导
本小节推导了在满足
${u_m}$ 的最低单位带宽速率需求的条件下,${p_m}$ 的取值范围。令式(4)中的
$m = M$ ,可推出${P_{_M}}$ 的取值范围满足:$${P_{_M}} \geqslant {c\alpha _{_M}}$$ (8) 式中,
${\alpha _m} = \dfrac{{{\sigma ^2}}}{{{{\left| {{h_m}} \right|}^2}}}$ ,m=1, 2,···,M。令式(4)中的$m = M - 1$ ,可推出${p_{_{\left( {M - 1} \right)}}}$ 的取值范围满足:$${p_{_{\left( {M - 1} \right)}}} \geqslant c(c + 1){\alpha _{_{(M - 1)}}}$$ (9) 令式(4)中的
$m = M - 2$ ,可推出${p_{_{\left( {M - 2} \right)}}}$ 的取值范围满足:$${p_{_{\left( {M - 2} \right)}}} \geqslant c{(c + 1)^2}{\alpha _{_{(M - 2)}}}$$ (10) 令式(4)中的
$m = M - 3$ ,可推出${p_{_{\left( {M - 3} \right)}}}$ 的取值范围满足:$${p_{_{\left( {M - 3} \right)}}} \geqslant c{(c + 1)^3}{\alpha _{_{(M - 3)}}}$$ (11) 令式(4)中的
$m = M - 4$ ,可推出${p_{_{\left( {M - 4} \right)}}}$ 的取值范围满足:$${p_{_{\left( {M - 4} \right)}}} \geqslant c{(c + 1)^4}{\alpha _{_{(M - 4)}}}$$ (12) 采用归纳法可得,
${p_m}$ 的取值满足:$${p_m} \geqslant c{(c + 1)^{M - m}}{\alpha _m}$$ (13) 因此,
$p_m^{\min }$ 的取值为:$$p_m^{\min } = c{(c + 1)^{M - m}}{\alpha _m}$$ (14) 2.2 总功率为常数时的功率分配
若直接求解式(7)中的优化问题,则要采取遍历的方法,复杂度极高。为此,先求解所有用户的总功率
$P$ 为一常数时最大的EE及其对应的功率分配,然后再求解总功率$P$ 变化时最大化EE的功率分配。当所有用户的总功率
$P$ 为某一常数且$P \geqslant \displaystyle\sum\limits_{m = 1}^M {p_m^{\min }}$ 时,最大化EE的功率分配优化问题可以表示为:$$ \begin{split} & \mathop {\max }\limits_{{p_m},\;m = 1,2, \cdots ,M} \frac{{{{\log }_2}\left( {1 + \displaystyle\sum\limits_{m = 1}^M {{p_m}{G_m}} } \right)}}{{P + {P_c}}} \\ & \qquad\quad {\rm{s.t.}}{\rm{ }}\sum\limits_{m = 1}^M {{p_m}} = P \\ & \qquad\quad {\rm{ }}p_m^{\min } \leqslant {p_m} \leqslant p_m^{\max } \end{split} $$ (15) 式(15)所示的优化问题等效于最大化
$\displaystyle\sum\limits_{m = 1}^M {{p_m}{G_m}}$ 。由于${G_1} \geqslant {G_2} \geqslant \cdots \geqslant {G_M}$ ,若不考虑约束条件,则${p_{_1}} = P$ 且${p_i} = 0\left( {i = 2,3, \cdots ,M} \right)$ 时,$\displaystyle\sum\limits_{m = 1}^M {{p_m}{G_m}}$ 达到最大值。然而,每个用户都有速率需求和最大发送功率约束,因此,当第2个用户至第M个用户刚好满足最低速率需求,并且将其余的功率都分配给第一个用户时,$\displaystyle\sum\limits_{m = 1}^M {{p_m}{G_m}}$ 达到最大值。式(15)所示的优化问题的解为:$$ \left\{ \begin{aligned} & {{p_m} = p_m^{\min }\quad m = 2,3, \cdots ,M} \\ & {p_{_1}} = \min \left\{ {P - \sum\limits_{m = 2}^M {p_m^{\min }} ,p_1^{\max }} \right\} \end{aligned} \right. $$ (16) 为了便于后续的推导,此处假定
$P - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} \leqslant p_1^{\max }$ ,即式(15)所示的优化问题的解为:$$ \left\{ \begin{aligned} & {{p_m} = p_m^{\min }\quad m = 2,3, \cdots ,M} \\ & {p_{_1} = P - \sum\limits_{m = 2}^M {p_m^{\min }} } \end{aligned} \right. $$ (17) 此时的EE为:
$$ e\left( P \right) = \frac{{{{\log }_2}\left( {1 + {G_1}\left( {P - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} } \right) + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }{G_m}} } \right)}}{{P{\rm{ + }}{P_c}}} $$ (18) 由式(18)可得出,为
${u_m}$ 分配功率$p_m^{\min }$ 且将其余的功率都分配给${u_1}$ 时,m=2, 3, ··· , M,系统的EE最高。2.3 总功率变化时的功率分配
所有用户的总功率
$P$ 为某一常数时,最大的能量效率$e\left( P \right)$ 如式(18)所示。本小节求解总功率$P$ 变化时最大化EE的功率分配。根据式(18),将式(7)中的优化问题转化为:
$$ \begin{split} & \qquad\qquad\qquad\qquad\quad \mathop {\max }\limits_P e\left( P \right) = \\ & \mathop {\max }\limits_P \frac{{{{\log }_2}\left( {1 + {G_1}\left( {P - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} } \right) + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }{G_m}} } \right)}}{{P{\rm{ + }}{P_c}}}{\rm{ }} \\ & \qquad{\rm{ s.t.}}\ \ {\rm{ }}C1:{\rm{ }}\sum\limits_{m = 1}^M {p_m^{\min }} \leqslant P \leqslant \sum\limits_{m = 1}^M {p_m^{\max }} {\rm{ }}\quad \forall m \\ & \qquad\quad\ \ C2:P - \sum\limits_{m = 2}^M {p_m^{\min }} \leqslant p_1^{\max }{\rm{ }}\quad \forall m \end{split} $$ (19) 式中,约束条件
$C2$ 表示为第1个用户分配的功率不能高于该用户的最高发送功率。求
$e\left( P \right)$ 关于$P$ 的导数可得:$$ \begin{split} & \frac{{\partial e\left( P \right)}}{{\partial P}} = \frac{{\dfrac{{{G_1}\left( {P + {P_c}} \right)}}{{\left[ {1 + {G_1}\left( {P - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} } \right) + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }{G_m}} } \right]\ln 2}}}}{{{{\left( {P + {P_c}} \right)}^2}}} -\\ & \qquad \frac{{{{\log }_2}\left( {1 + {G_1}\left( {P - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} } \right) + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }{G_m}} } \right)}}{{{{\left( {P + {P_c}} \right)}^2}}} \end{split} $$ (20) 令
$\delta = \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }}$ 且$\chi = 1 + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }{G_m}}$ ,式(20)可转化为:$$ \begin{split} & \frac{{\partial e\left( P \right)}}{{\partial P}}{\rm{ = }}\frac{{\dfrac{{{G_1}\left( {P + {P_c}} \right)}}{{\ln 2\left[ {\chi + {G_1}\left( {P - \delta } \right)} \right]}}}}{{{{\left( {P + {P_c}} \right)}^2}}} {\rm{ }} - \frac{{{{\log }_2}\left[ {\chi + {G_1}\left( {P - \delta } \right)} \right]}}{{{{\left( {P + {P_c}} \right)}^2}}} = \\ & \qquad\qquad\qquad\qquad \frac{{\beta \left( P \right)}}{{{{\left( {P + {P_c}} \right)}^2}}} \\ \end{split} $$ (21) 式中,
$\beta \left( P \right)$ 的表达形式为:$$ \begin{split} & \beta \left( P \right) = \dfrac{{{G_1}\left( {P + {P_c}} \right)}}{{\left[ {{G_1}\left( {P - \delta } \right) + \chi } \right]\ln 2}} - \\ & {\rm{ }} \frac{{\left[ {{G_1}\left( {P - \delta } \right) + \chi } \right]\ln 2{{\log }_2}\left[ {{G_1}\left( {P - \delta } \right) + \chi } \right]}}{{\left[ {{G_1}\left( {P - \delta } \right) + \chi } \right]\ln 2}} \end{split} $$ (22) 计算可得,
$P > \dfrac{{{2^{2\left( {{G_1}\delta - \chi + 2} \right)}} + {G_1}\delta - \chi }}{{{G_1}}}$ 时,$\,\beta \left( P \right) < 0$ ;$P < \dfrac{{1 + {G_1}\delta - \chi }}{{{G_1}}}$ 时,$\,\beta \left( P \right) > 0$ ;因此,必定存在${P^ * }$ ,使得$\beta \left( {{P^ * }} \right) = 0$ 。当$P < {P^ * }$ 时,$\beta \left( P \right) > 0$ ,$\dfrac{{\partial e\left( P \right)}}{{\partial P}} > 0$ ,$e\left( P \right)$ 单调递增;当$P > {P^ * }$ 时,$\beta \left( P \right) < 0$ ,$\dfrac{{\partial e\left( P \right)}}{{\partial P}} < 0$ ,$e\left( P \right)$ 单调递减,因此,$P = {P^ * }$ 时,$e\left( P \right)$ 达到最大值。由于无法给出
${P^ * }$ 的闭合表达式,可采用二分法找到${P^ * }$ ,步骤如下:1)令
${P_1} = \dfrac{{1 + {G_1}\delta - \chi }}{{{G_1}}}$ ,${P_2} = \dfrac{{{2^{2\left( {{G_1}\delta - \chi + 2} \right)}} + {G_1}\delta - \chi }}{{{G_1}}}$ ,用${P_0}$ 表示${P_1}$ 和${P_2}$ 的中间值,即${P_0} = \dfrac{{{P_1} + {P_2}}}{2}$ ,计算$\beta \left( {{P_0}} \right)$ ;2)若
$\beta \left( {{P_0}} \right) > \varepsilon $ ,$\varepsilon $ 是预先设定的非常小的正数,令${P_1} = {P_0}$ 且${P_2} = \dfrac{{{2^{2\left( {{G_1}\delta - \chi + 2} \right)}} + {G_1}\delta - \chi }}{{{G_1}}}$ ,执行步骤3),若$\beta \left( {{P_0}} \right) < - \varepsilon $ ,令${P_1} = \dfrac{{1 + {G_1}\delta - \chi }}{{{G_1}}}$ 且${P_2} = {P_0}$ ,执行步骤3),若$\left| {\beta \left( {{P_0}} \right)} \right| < \varepsilon $ ,则令${P^ * } = {P_0}$ ,不再执行后面的步骤;3)令
${P_0} = \dfrac{{{P_1} + {P_2}}}{2}$ ,计算$\beta \left( {{P_0}} \right)$ ,重复步骤2),直至$\left| {\beta \left( {{P_0}} \right)} \right| < \varepsilon $ 。采用二分法找到
${P^ * }$ 后,若$\displaystyle\sum\limits_{m = 1}^M {p_m^{\min }} \geqslant {P^ * }$ ,则$P = \displaystyle\sum\limits_{m = 1}^M {p_m^{\min }} $ 时,系统的EE最大,此时为$u_m^{}$ 分配功率$p_m^{\min }$ ,m=1, 2, ···, M。若$\displaystyle\sum\limits_{m = 1}^M {p_m^{\min } \!< \! } {P^ * } \!<\! p_1^{\max } + \!\!\! \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }}$ ,则$P = {P^*}$ 时,系统的EE最大,此时为${u_1}$ 分配功率${P^*} - \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} $ ,为$u_m^{}$ 分配功率$p_m^{\min }$ ,m=2, 3, ···, M。若${P^ * } \geqslant p_1^{\max } + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} $ ,则$P = p_1^{\max } + \displaystyle\sum\limits_{m = 2}^M {p_m^{\min }} $ 时,系统的EE最大,此时,为${u_1}$ 分配功率$p_1^{\max }$ ,为$u_m^{}$ 分配功率$p_m^{\min }$ ,m=2, 3, ···, M。从所提算法中可以看出:当总功率
$P < {P^ * }$ 时,随着$P$ 的增大,为信道质量最优的用户分配的功率也随着增大,从而提高了EE。当总功率$P$ 超过${P^ * }$ 时,即使再增大总功率,最优的总功率以及为各用户分配的功率仍保持不变,即EE保持不变。2.4 复杂度及收敛性分析
所提方案、文献[19]和文献[20]都采用迭代的方法求解最大化EE的功率分配优化问题,因此3种方案的计算复杂度都与迭代次数有关。文献[19]先根据算法3更新每个用户的功率,再将用户功率代入算法2进行迭代求解EE,用
${I_1}$ 表示更新每个用户功率的迭代次数即算法3的迭代次数,用${I_2}$ 表示算法2的迭代次数。文献[20]将最大化EE的优化问题转化为多个最大化和速率的子问题,用${I_1}$ 表示注水算法的迭代次数,用${I_2}$ 表示该文中算法2的迭代次数。用${I_1}$ 表示所提方案的二分法的迭代次数。表1列出了3种方案的计算复杂度。所提方案、文献[19]和文献[20]的计算复杂度分别与
${I_1}M$ 、${I_1}{I_2}M$ 和${I_1}{I_2}{M^2}$ 成正比。若${I_1} = {I_2} = 10$ 且M=20,所提方案的计算量大约分别是文献[19]和文献[20]的3/50、4/500。所提二分法的步骤1中
$\beta \left( {{P_1}} \right) > 0$ 且$\beta \left( {{P_2}} \right) < 0$ ,因此,必定存在${P^ * }$ ,使得$\left| {\beta \left( {{P^ * }} \right)} \right| < \varepsilon $ ,故${I_1}$ 是有限值。因此,本文所提方案是收敛的,并且其计算复杂度显著低于文献[19]和文献[20]。3. 性能比较及仿真
本节仿真了所提方案和文献[19-20]的EE。参数设置如下:信道包含小尺度衰落和路径损耗,小尺度衰落服从独立的瑞利分布,路径损耗模型是
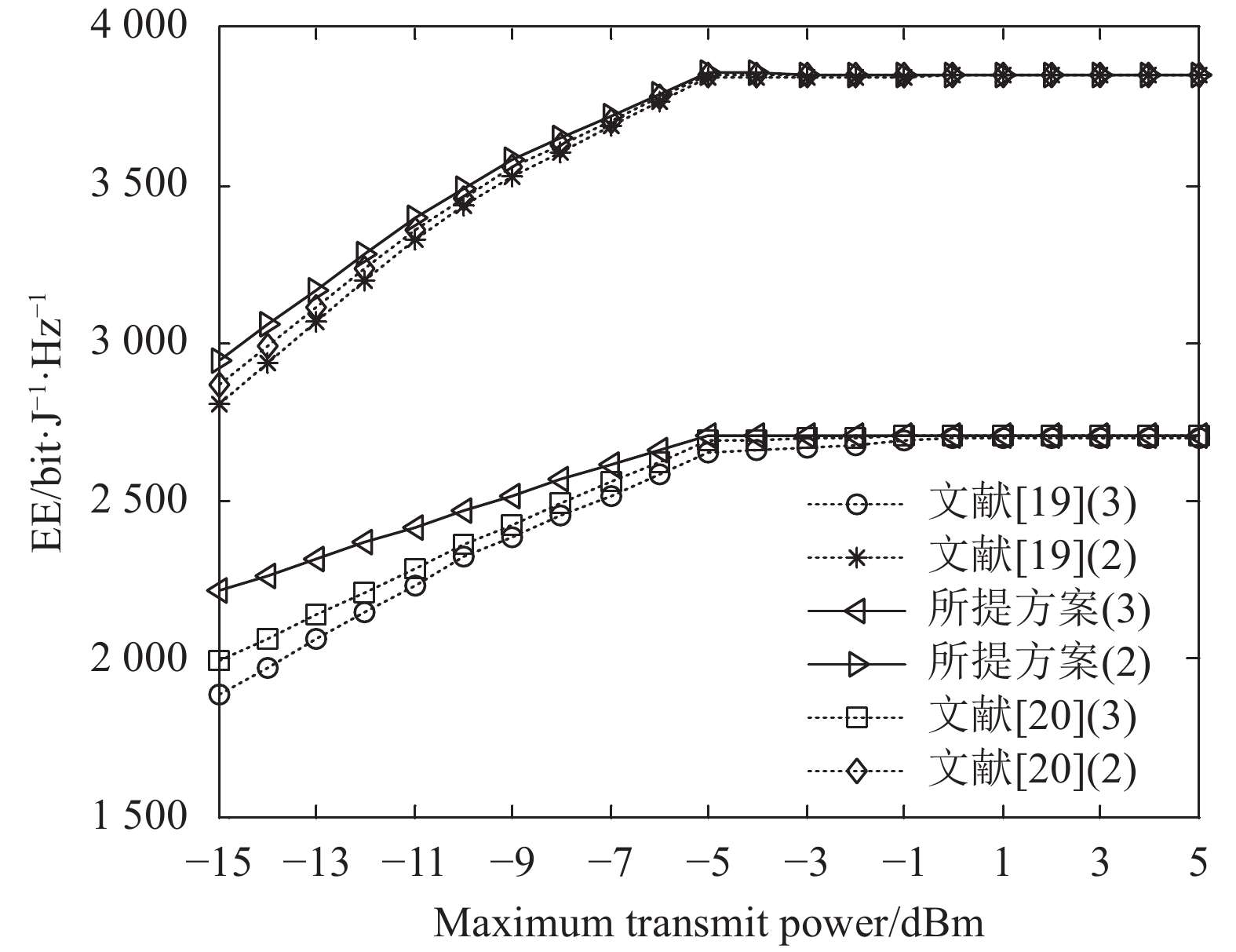
$128 + 35{\lg}\left( d \right)$ ,其中$d$ 是收发设备之间的距离,设置$d = 10\;{\rm{m}}$ ,信道带宽为$180\;{\rm{KHz}}$ ;噪声功率谱密度是$- 174\;{\rm{dBm/Hz}}$ ;每个用户的固定功率消耗是$0\;{\rm{dBm}}$ 。假定单个基站分别服务了2个和3个用户,即用户数目分别为M=2和M=3。所有用户的最大发送功率$p_m^{\max }$ 均相等,m=1, 2, ··· , M,$R_{}^{\min }$ 有两种取值,${R^{\min }} = 1$ 和${R^{\min }} = 1.5$ 。图2仿真了
${R^{\min }} = 1$ 时,3种方案的EE。所提方案用实线表示,对比方案用虚线表示,图例括号中的参数表示用户个数,图3也采用此种表示方法。从图2中可看出,2用户场景下系统EE高于3用户的EE。原因在于,第3个用户的信道质量较差,导致系统EE降低。从图2中还能看出,信噪比(signal to noise ratio, SNR)范围为[−15 dBm,5 dBm]时,随着${p^{\max }}$ 的增大,系统的EE先增大后保持不变。因为随着总功率$P$ 的增大,为信道质量最优的用户分配的功率以及系统的EE也随着增大,当总功率超过${P^ * }$ 时,即使再增大总功率$P$ ,最优的总功率以及为各用户分配的功率仍保持不变,即EE保持不变。此外,SNR范围为[−15 dBm,0 dBm]时,所提方案的EE高于对比方案。图3仿真了
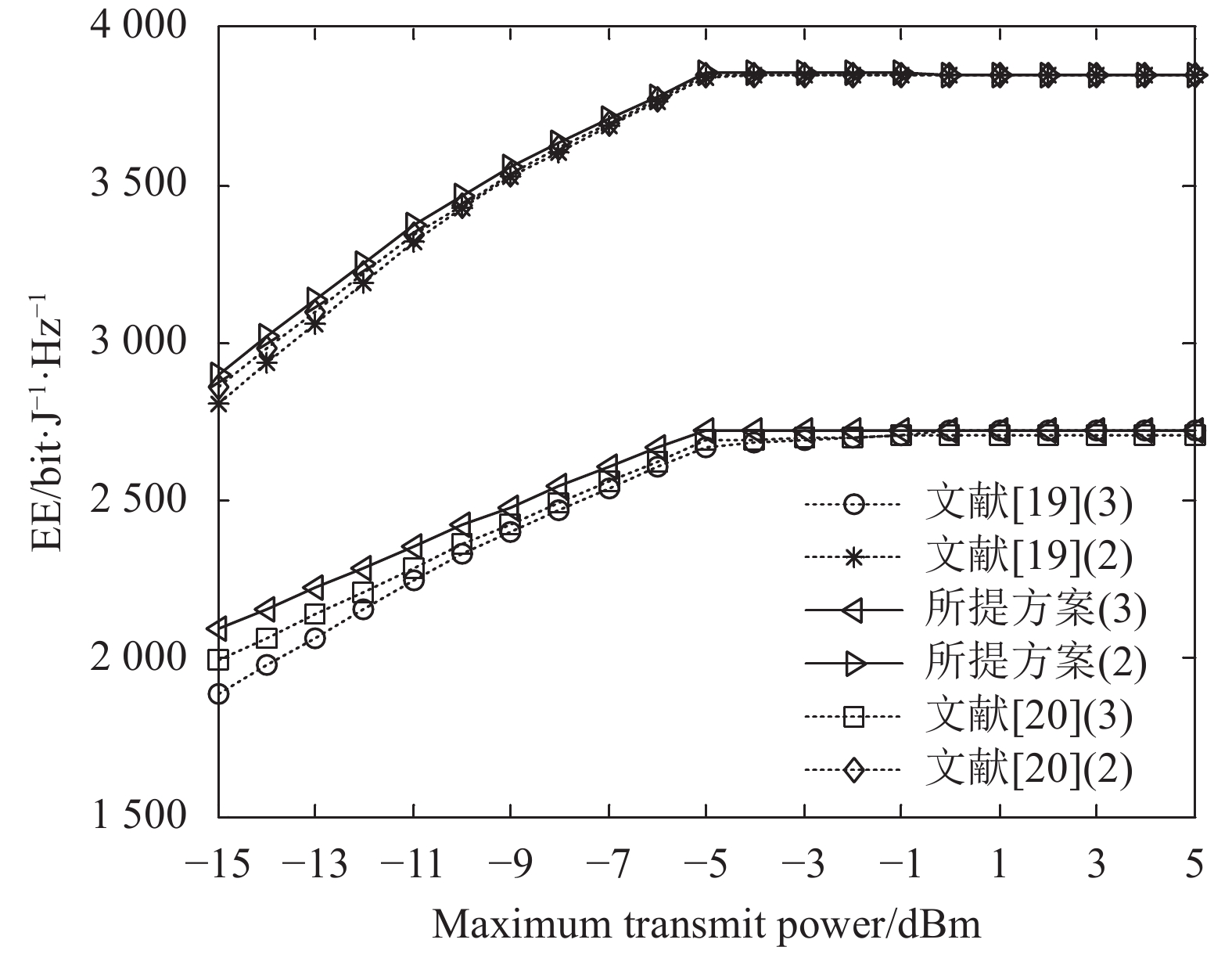
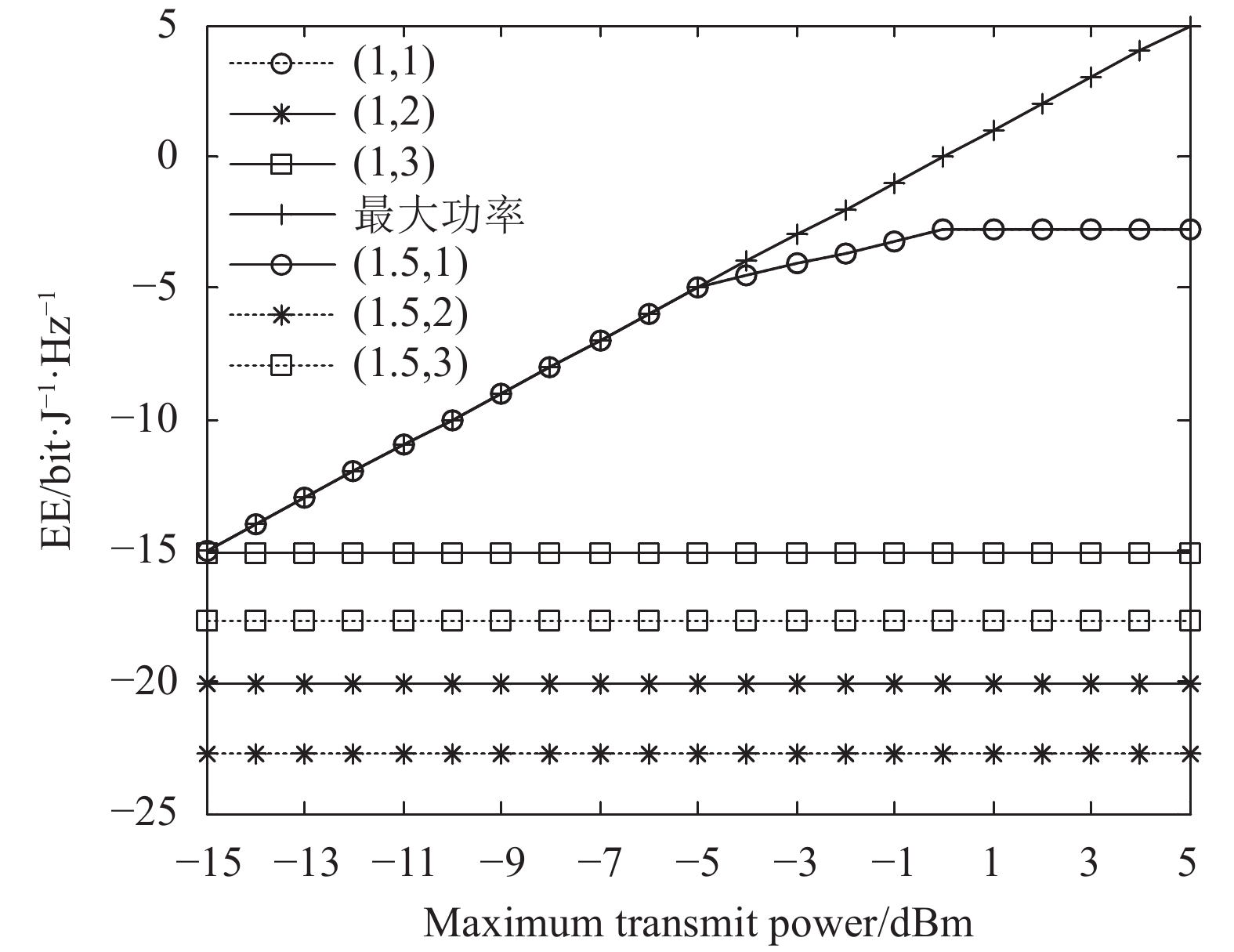
${R^{\min }} = 1.5$ 时,3种方案的EE。从图3可看出,2用户场景下系统EE高于3用户的EE;随着SNR的增大,系统的EE先增大后保持不变;SNR范围为[−15 dBm,−5 dBm]时,所提方案的EE高于对比方案。比较图2和图3可看出,${R^{\min }} = 1$ 时的EE高于${R^{\min }} = 1.5$ 时的EE,因为${R^{\min }}$ 越低,为信道质量差的用户分配的功率越低,从而为信道质量优的用户分配的功率越高,因此系统的EE越高。图4仿真了为3个用户分配的功率与最大发送功率之间的关系,仿真中小尺度衰落设置为
${\left| {{h_1}} \right|^2} = 1.10 \times {10^{ - 9}}$ ,${\left| {{h_2}} \right|^2} = 1.34 \times {10^{ - 10}}$ ,${\left| {{h_3}} \right|^2} = 4.25 \times {10^{ - 11}}$ 。图例括号中的第一个参数表示最低速率需求${R^{\min }}$ ,第二个参数表示用户。从图中能看出,SNR为[−15 dBm,−5 dBm]时,为${u_1}$ 分配最大发送功率;SNR为[0 dBm,5 dBm]时,${u_1}$ 的功率不再随着最大发送功率的增加而增加,而是始终保持不变;无论SNR怎么变化,始终为${u_2}$ 和${u_3}$ 分配所需的最低功率。从图中能还看出,${R^{\min }} = 1$ 时,为${u_2}$ 和${u_3}$ 分配的功率曲线低于${R^{\min }} = 1.5$ 时的${u_2}$ 和${u_3}$ 分配的功率曲线,因为${R^{\min }}$ 越小,单用户所需的最低功率越小。4. 结 束 语
本文研究了上行NOMA系统中最大化EE的功率分配方案。基于用户的最低速率需求和最大发送功率限制,建立最大化EE的功率分配优化问题,基于二分法得到最大的EE对应的所有用户的总功率,进而得到为单个用户分配的功率。仿真结果显示,所提方案的EE高于或等于已有方案的EE。上行系统中的多个簇采用正交频段时,不同簇的用户间的功率不存在制约关系,单簇的功率分配方案可直接应用于多簇场景中的每个簇。由于所提功率分配方案是在给定子信道分配下进行的,如何分配子信道以进一步提高系统性能有待于进一步研究。
-
[1] 杨正. 5G移动网络非正交多址接入及相关技术研究[D]. 四川: 西南交通大学, 2016. YANG Zheng. Investigation of non-orthogonal multiple access and related techniques for the 5th generation mobile networks[D]. Sichuan: Southwest Jiaotong Uni-versity, 2016.
[2] 赵钊. 上行NOMA系统中的用户分簇和功率分配[D]. 北京: 北京邮电大学, 2018. ZHAO Zhao. User clustering and allocation for uplink NOMA system[D]. Beijing: Beijing University of Posts and Telecommunications, 2018.
[3] DING Zhi-guo, LIU Yuan-wei, CHOI J, et al. Application of non-orthogonal multiple access in LTE and 5G networks[J]. IEEE Communications Magazine, 2017, 55(2): 185-191. DOI: 10.1109/MCOM.2017.1500657CM
[4] WANG Jian-heng, PENG Qian, HUANG Yong-ming, et al. Convexity of weighted sum rate maximization in NOMA systems[J]. IEEE Signal Processing Letters, 2017, 24(9): 1323-1327. DOI: 10.1109/LSP.2017.2722546
[5] ZHANG Hai-jun, WANG Bao-bao, JIANG Chun-xiao, et al. Energy efficient dynamic resource optimization in NOMA system[J]. IEEE Transactions on Wireless Communications, 2018, 17(9): 5671-5683. DOI: 10.1109/TWC.2018.2844359
[6] YANG Zhao-hui, XU Wei, PAN Cun-hua, et al. On the optimality of power allocation for NOMA downlinks with individual QoS constraints[J]. IEEE Communications Letters, 2017, 21(7): 1649-1652. DOI: 10.1109/LCOMM.2017.2689763
[7] ZHU Jian-yue, WANG Jia-heng, HUANG Yong-ming, et al. On optimal power allocation for downlink non-orthogonal multiple access systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2744-2757.
[8] FU Y, SALAUN L, SUNG C W, et al. Subcarrier and power allocation for the downlink of multicarrier NOMA systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(12): 11833-11847. DOI: 10.1109/TVT.2018.2875601
[9] ZHANG Yi, WANG Hui-ming, ZHENG Tong-xing, et al. Energy-efficient transmission design in non-orthogonal multiple access[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2852-2857. DOI: 10.1109/TVT.2016.2578949
[10] LIU Qian, GAO Hui, TAN Fang-qing, et al. Energy efficient resource allocation in multi-user downlink non-orthogonal multiple access systems[C]//2017 IEEE Global Communications Conference. Singapore: IEEE, 2017: 1-6.
[11] FANG Fang, ZHANG Hai-jun, CHENG Ju-lian, et al. Energy-efficient resource allocation for downlink non-orthogonal multiple access network[J]. IEEE Transactions on Communications, 2016, 64(9): 3722-3732. DOI: 10.1109/TCOMM.2016.2594759
[12] ZHAI Dao-sen, DU Jian-bo. Spectrum efficient management for multi-carrier-based NOMA networks: A graph-based method[J]. IEEE Wireless Communications, 2018, 7(3): 388-391. DOI: 10.1109/LWC.2017.2779485
[13] SEDAGHAT M A, MULLER R R. On user pairing in uplink NOMA[J]. IEEE Transactions on Wireless Communications, 2018, 17(5): 3474-3485. DOI: 10.1109/TWC.2018.2815005
[14] RUBY R, ZHONG Shu-xin, YANG Hai-liang, et al. Enhanced uplink resource allocation in non-orthogonal multiple access systems[J]. IEEE Transactions on Wireless Communications, 2018, 17(3): 1432-1444. DOI: 10.1109/TWC.2017.2778105
[15] LV Guo-cheng, LI Xu-nan, SHANG R, et al. Dynamic resource allocation for uplink non-orthogonal access systems[J]. IET Communications, 2018, 12(6): 649-655. DOI: 10.1049/iet-com.2017.0972
[16] SUN Qi, HAN Shuang-feng, Chin-lin I, et al. Energy efficiency optimization for fading mimo non-orthogonal multiple access systems[C]//2015 IEEE International Conference on Communications. London, UK: IEEE, 2015: 2668-2673.
[17] ZHANG Yi, WANG Hui-ming, ZHENG Tong-xing, et al. Energy-efficient transmission design in non-orthogonal multiple access[J]. IEEE Transactions on Vehicular Technology, 2016, 66(3): 2852-2857.
[18] ZENG Ming, YADAV A, OCTAVIA A, et al. Energy-efficient power allocation for uplink NOMA[C]//2018 IEEE Global Communications Conference. United Arab Emirates: IEEE, 2018: 1-6.
[19] ZENG Ming, YADAV A, DOBRE O C, et al. Energy-efficient joint User-RB association and power allocation for uplink hybrid NOMA-OMA[J]. IEEE Internet of Things Journal, 2019, 6(3): 5119-5131. DOI: 10.1109/JIOT.2019.2896946
[20] ZENG Ming, NGUYEN N , DOBRE O C, et al. Spectral and energy-efficient resource allocation for multi-carrier uplink NOMA systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(9): 9293-9296. DOI: 10.1109/TVT.2019.2926701
-
期刊类型引用(2)
1. 何华,梁彦霞,刘原华. 非正交多址系统中基于公平性改善的双层挤压迭代功率分配方法. 计算机应用研究. 2024(06): 1815-1819 .  百度学术
百度学术
2. 杨普,曲庆悦,申逸飞,刘毅. 能量效率最大化的非正交多址接入系统功率分配方法. 吉林大学学报(工学版). 2024(08): 2370-2377 .  百度学术
百度学术
其他类型引用(5)

 ISSN
ISSN 


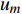
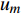
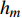
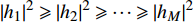
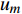
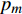
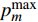
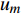
 下载:
下载: