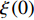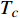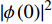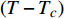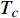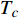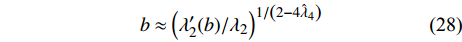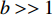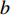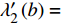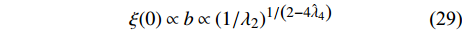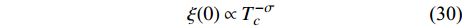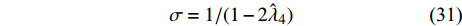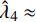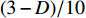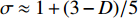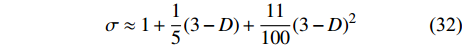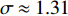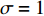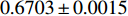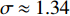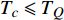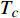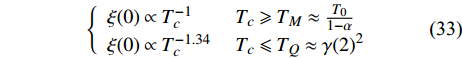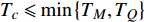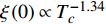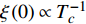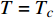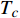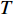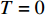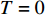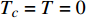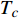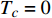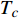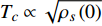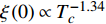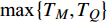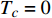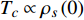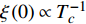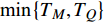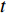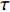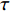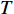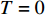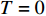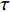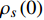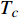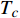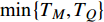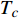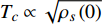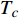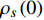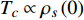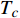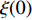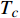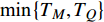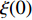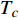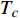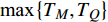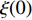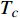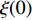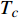Quantum Fluctuations and the Anomalous Two-Class Scaling in the Overdoped Cuprate Films
-
摘要: 通过引入虚时间变量,将绝对零度附近的金兹堡−朗道方程推广为一个精确的相对论方程。基于该方程所建立的虚时量子场论,描述过掺杂铜氧化物超导材料在绝对零度附近的量子临界现象。利用虚时量子场论框架,理论推导出在
$ {\rm{L}}{{\rm{a}}_{2 - x}}{\rm{S}}{{\rm{r}}_x}{\rm{Cu}}{{\rm{O}}_4} $ 超导薄膜的过掺杂区域所观测到的零温超流相位刚度与相变温度之间的反常两段标度,且理论计算结果与实验测量值吻合良好。该研究推测:处于绝对零度附近的过掺杂超导薄膜中,零温相干长度与相变温度也服从一个两段标度,理论得到的两个临界指数1和1.34有待实验的检验。-
关键词:
- 平均场近似 /
- 过掺杂铜氧化物超导薄膜 /
- 量子涨落 /
- 库珀电子对的虚时相对论方程
Abstract: By introducing the imaginary time, we show that Gor’kov’s Ginzburg–Landau equation at zero temperature can be extended to an exact relativistic form. Based on this equation, we propose a quantum field theory with the imaginary time, which is intended to describe the quantum critical phenomena in the zero-temperature overdoped cuprate. By using such a quantum field theory, we show that the anomalous two-class scaling between the transition temperature$ {T_c} $ and zero-temperature superfluid phase stiffness$\;{\rho _s}\left( 0 \right)$ observed in the overdoped side of single-crystal${\rm{L}}{{\rm{a}}_{2 - x}}{\rm{S}}{{\rm{r}}_x}{\rm{Cu}}{{\rm{O}}_4}$ films can be derived exactly. In this paper, we further theoretically show that, for 2-dimensional overdoped cuprate films, the transition temperature$ {T_c} $ and the zero-temperature coherence length$ \xi \left( 0 \right) $ will obey a two-class scaling as well. When the transition temperature$ {T_c} $ is less than a characteristic temperature scale${T_{Q}}$ , the transition temperature$ {T_c} $ and the zero-temperature coherence length$ \xi(0) $ obeys the scaling$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ , which is a quantum critical behavior. Nevertheless, when the transition temperature is larger than another characteristic temperature scale${T_{M}}$ , the scaling relationship will yield$ \xi \left( 0 \right) \propto T_c^{ - 1} $ , which is a mean-field behavior. -
量子临界现象是凝聚态物理中的一个重要研究领域,它的产生源于量子涨落。量子涨落也称为“零点运动”,即在绝对零度(零温)附近,由于海森堡不确定性原理的作用,原子与分子不可能处于静止,而这种零点运动会诱发相变−“量子相变”。量子临界现象就是这种相变所对应的临界现象。一般来说,在有限温度下,热涨落都存在,所以量子涨落的效果只有在温度趋于绝对零度附近时才会显现出来,此时热涨落的效果可以忽略不计。研究量子临界现象的理论框架基于Hertz的先驱性工作[1]。由于量子临界现象发生在温度趋于零温的体系,Hertz将统计物理配分函数中的参量“温度
$ T $ ”的倒数作为第4维“虚时间”(本质上是松原时间),从而建立了虚时量子场论以描述强关联系统中的量子涨落现象。目前,Hertz的虚时量子场论已经成为研究量子临界现象的基本分析架构[1-2]。实验中,零温超流相位刚度(zero-temperature superfluid phase stiffness)$\;{\rho _s}\left( 0 \right)$ 与相变温度$ {T_c} $ 是刻画超导体中量子临界现象的两个重要参量[3-7]。现已知在高度欠掺杂铜氧化物超导材料中发生的超导−绝缘相变可能是一类量子临界现象,其中$\;{\rho _s}\left( 0 \right)$ 与$ {T_c} $ 近似服从亚线性标度$ {T_c} \propto {\rho _s}{\left( 0 \right)^\delta } $ ,且$ \delta \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2} $ 。尽管如此,但就高度过掺杂铜氧化物超导材料中发生的超导−金属相变,对于其基本性质仍旧缺乏足够的了解。文献[8]在充分调查了超低温下
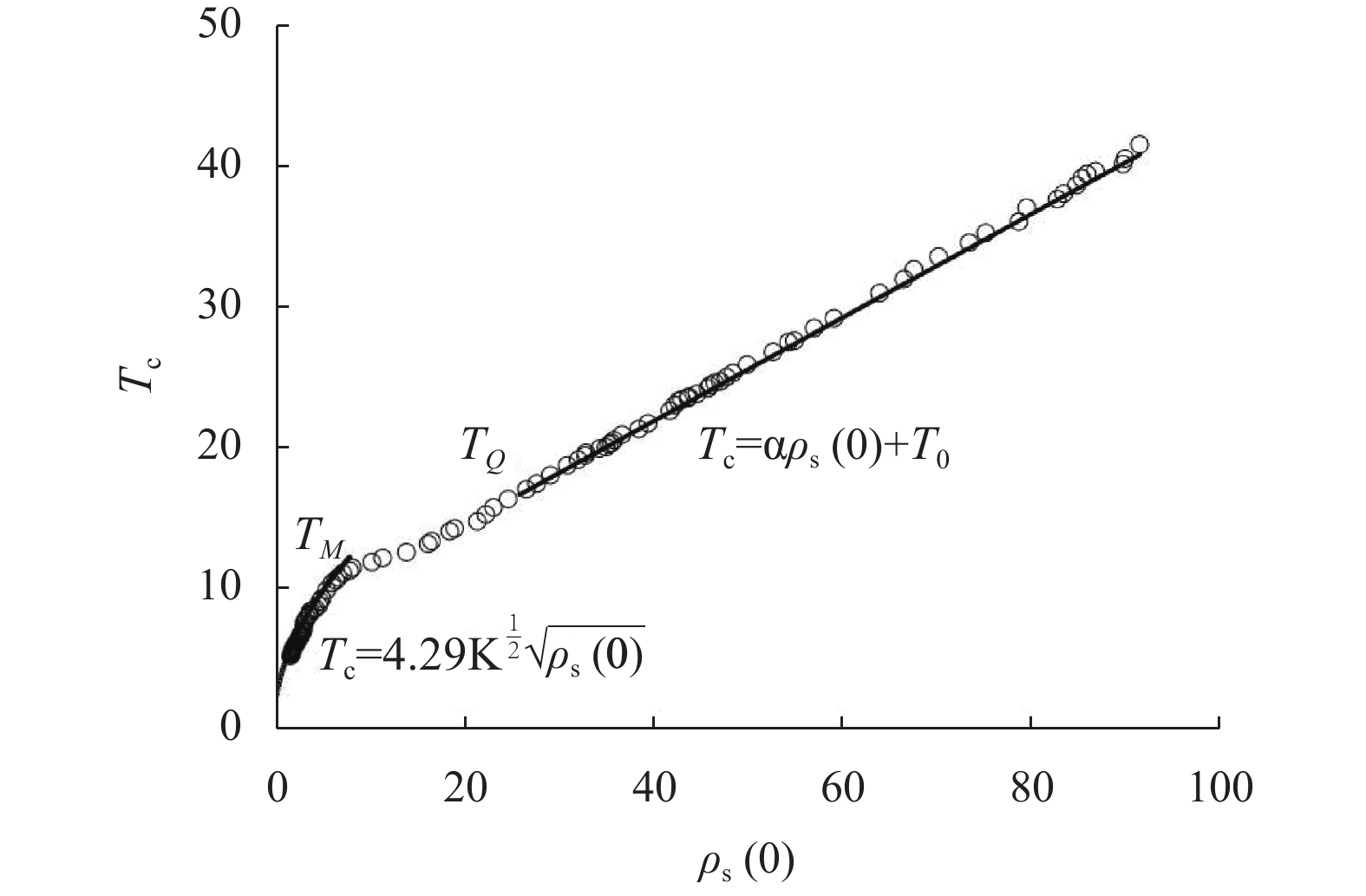
${\rm{L}}{{\rm{a}}_{2 - x}}{\rm{S}}{{\rm{r}}_x}{\rm{Cu}}{{\rm{O}}_4}$ (LSCO) 单晶薄膜过掺杂区域中$ \;{\rho _s}\left( 0 \right) $ 与$ {T_c} $ 的性质后,公布了一个引起广泛关注的反常两段标度:当$ {T_c} \geqslant {T_{M}} $ 时存在线性标度$ {T_c} = \alpha {\rho _s}\left( 0 \right) + {T_0} $ ;当$ {T_c} \leqslant {T_{Q}} $ 时存在亚线性标度$ {T_c} = \gamma \sqrt {{\rho _s}\left( 0 \right)} $ 。其中,$ {T_{M}} \approx 12\;{\rm{K}} $ ,$ {T_{Q}} \approx 15\;{\rm{K}} $ ,$ \alpha=0.37 \pm 0.02 $ ,$T_{0}=(7.0 \pm 0.1) \;\rm{K}$ ,$\gamma=(4.2 \pm $ $ 0.5)\; {\rm{K}}^{1 / 2}$ 。反常两段标度中的线性标度
$ {T_c} \propto {\rho _s}\left( 0 \right) $ 已经被大量的实验所观测到,它被称为“Homes定律”[9-10],并被Abrikosov-Gor’kov 平均场理论所解释[10-11]。文献[12]已经利用该平均场理论给出了$ \alpha $ 的正确理论值。尽管如此,反常两段标度中的亚线性标度却不能被平均场理论解释,因此文献[13-14]推断文献[8]的实验发现与平均场理论不相容,对此还给出了进一步的观测证据:随着掺杂程度的增加,LSCO材料变得越来越像金属并且呈现出超导体向金属态转变的量子相变。为了解释反常两段标度中的亚线性标度
$ {T_c} \propto $ $ \sqrt {{\rho _s}\left( 0 \right)} $ ,文献[15-18]基于Hertz的虚时量子场论框架,将零温T=0处的金兹堡−朗道方程推广为精确的相对论形式,其中没有任何的唯象参数。为了引述方便,下文称该方程为“相对论金兹堡−朗道方程”。不过严格来说,该方程应该称为“零温库珀电子对的虚时相对论方程”,因为这里的“时间”并不是物理世界的时间,只是由温度的倒数衍生出来的虚时间。显然,严格意义上的相对论金兹堡−朗道方程应该在物理时空中,且不应该局限在绝对零度附近。文献[17-18]利用相对论金兹堡−朗道方程精确的推导出反常两段标度,计算结果表明,当相变温度$ {T_c} $ 较大时,系统远离量子临界点$ {T_c} = 0 $ ,所以平均场近似有效,这导致线性标度$ {T_c} \propto {\rho _s}\left( 0 \right) $ 成立;而当相变温度$ {T_c} $ 趋于0时,系统靠近量子临界点$ {T_c} = 0 $ ,这使得量子涨落被放大,从而导致平均场近似被破坏,所以线性标度转变为亚线性标度$ {T_c} \propto \sqrt {{\rho _s}\left( 0 \right)} $ 。值得注意的是,文献[16-18]的反常两段标度给出的参数$ \gamma $ 、$ {T_M} $ 、$ {T_Q} $ 的理论值与文献[8]的实验测量值吻合良好,这是对上述相对论金兹堡−朗道方程有力的支持。目前国际上也有其他研究小组[19-21]尝试利用唯象的理论来解释反常两段标度中线性标度与亚线性标度共存的特征,但都无法给出参数$ \gamma $ 、$ {T_M} $ 、$ {T_Q} $ 的实验值。相比之下,文献[16-18]的相对论金兹堡−朗道方程中没有任何的唯象参数,并且可以精确地解释$ \gamma $ 、$ {T_M} $ 、$ {T_Q} $ 的实验测量值。本文首先介绍相对论金兹堡−朗道方程的推导过程,并且指出反常两段标度是该方程的近似解。然后进一步从理论上推测,对于过掺杂铜氧化物超导薄膜,零温相干长度
$ \xi \left( 0 \right) $ 与相变温度$ {T_c} $ 也将服从一个两段标度:当$ {T_c} \geqslant {T_M} $ 时,存在标度$ \xi \left( 0 \right) \propto T_c^{ - 1} $ ;当$ {T_c} \leqslant {T_Q} $ 时,存在标度$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ 。这个两段标度是一个新的理论结果,将有待进一步的实验验证。与文献[8]在实验上所发现的反常两段标度一样,$ \xi \left( 0 \right) \propto T_c^{ - 1} $ 是一个平均场结果,而$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ 是量子涨落所诱发的反常标度。确证这个新的两段标度不仅具有验证相对论金兹堡−朗道方程的理论意义,也具有潜在的实用价值。如新的两段标度暗示,对于趋近绝对零度的过掺杂铜氧化物超导薄膜,当相变温度$ {T_c} $ 小于一个特征温标$ {T_Q} $ 时,量子涨落将会被放大,因此该薄膜是一种很好的激发量子涨落的材料。此外,随着量子退火算法在量子计算方面的突破[22-24],量子涨落的应用受到越来越多的关注。目前量子退火的基本运行原理是运用量子涨落的原理使得伊辛模型中的自旋方向发生改变,其产生量子涨落的方法主要基于对自旋施加横向磁场。利用其他方式产生量子涨落已经成为当前量子退火算法的一个潜在研究方向[25-26],从这个意义上来看,过掺杂铜氧化物超导薄膜可能在此方向具有潜在的应用价值。最后,本文统一使用自然单位制$ \hbar = c = {k_B} = 1 $ ,其中$ \hbar $ 代表约化普朗克常数,$ c $ 代表光速,$ {k_B} $ 代表玻尔兹曼常数。1. 相对论金兹堡−朗道方程
本文首先介绍虚时量子场论框架中的相对论金兹堡−朗道方程。文献[11]指出当温度
$ T $ 和相变温度$ {T_c} $ 满足关系$ \left| {T - {T_c}} \right| \approx 0 $ 时,利用BCS超导微观理论可以导出金兹堡−朗道方程:$$ \dfrac{1}{4 m_{e}^{*}} \nabla^{2} \psi(T)-\dfrac{1}{\lambda} \dfrac{T-T_{c}}{T_{c}} \psi(T) -\dfrac{1}{\lambda n_{s}(0)}|\psi(T)|^{2} \psi(T)=0 $$ (1) 式中,
$ |\psi(T)|^{2} $ 代表温度$ T $ 时的超流密度;$ \lambda= $ $ 7 \zeta(3) \varepsilon_{F} / 6 {\text{π}}^{2} T_{c}^{2} $ 。 ;$ {n_s}\left( 0 \right) $ 代表材料是各向均匀时的零温超流密度;$ \zeta \left( x \right) $ 代表黎曼函数;$ {\varepsilon _F} $ 是费米能量;$ m_e^* $ 代表电子静质量。重标波函数
$ \psi \left( T \right) $ $={\sqrt {4m_e^*} } \phi \left( T \right)$ ,则式(1)可写为拉格朗日函数[15-18]:$$ \begin{split} {\rm{L}}(T)= & |\nabla \phi(T)|^{2}+\dfrac{24 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} T_{c}^{2} \dfrac{\left(T-T_{c}\right)}{T_{c}}|\phi(T)|^{2}+ \\ & \qquad \dfrac{12 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} \dfrac{T_{c}^{2}}{\rho_{s}(0)}|\phi(T)|^{4} \end{split} $$ (2) 式中,
$ \rho_{s}(0)=n_{s}(0) / 4 m_{e}^{*} $ 代表零温超流相位刚度[8, 15]。式(2)能够被用于描述有限温度下的热临界现象,此时
$ {\left| {\phi \left( T \right)} \right|^2} $ 前面的系数是朗道定义的温度一次项,它正比于$ \left(T-T_{c}\right) $ 。式(2)的配分函数可以写为[27-29]:$$ Z\left( T \right) = \int {{{\left[ {D{\phi ^*}\left( T \right)} \right]}_\varLambda }\int {{{\left[ {D\phi \left( T \right)} \right]}_\varLambda }{{\rm{e}}^{ - \tfrac{1}{T}\int {{{\rm{d}}^D}{{q}}} L\left( T \right)}}} } $$ (3) 式中,
$ \varLambda = {1 \mathord{\left/ {\vphantom {1 a}} \right. } a} $ 表示动量截断;$ D $ 代表空间维度;$ a $ 代表超导材料中的晶格间距;$ {{q}} $ 代表空间坐标。随着制冷技术的提升,现在的实验条件可以将超导材料的温度降到一个接近绝对零度的范围,如
$ T < 0.3\;{\rm{K}} $ [8]。对处于绝对零度环境中的超导材料,式(2)可写为:$$ \begin{split} {\rm{L}}(T=0)= & |\nabla \phi(0)|^{2}-\dfrac{24 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} T_{c}^{2}|\phi(0)|^{2}+ \\ & \dfrac{12 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} \dfrac{T_{c}^{2}}{\rho_{s}(0)}|\phi(0)|^{4} \end{split} $$ (4) 值得注意的是,不同于
$ T > 0 $ 的情形,式(4)中$ {\left| {\phi \left( 0 \right)} \right|^2} $ 前面的系数不再是线性项$ \left(T-T_{c}\right) $ ,而是$ {T_c} $ 的二次项。这导致过掺杂超导材料在绝对零度附近的临界性质非常不同于热临界现象。更重要的是,$ T = 0 $ 是式(3)中的一个奇点,因此不能简单地将式(4)代入式(3)。为了处理零温$ T = 0 $ 的情形,需要考虑Hertz的虚时量子场论框架,即引入虚时间$ \tau \in[0,1 / T] $ ,其中$ T = 0 $ 。在虚时量子场论中,序参量$ \phi \left( 0 \right) $ 是空间坐标$ {{q}} $ 与虚时间$ \tau $ 的函数[1, 27],即$ \phi(0)=\phi(q, \tau) $ 。这意味着式(4)中还应当存在虚时间导数的线性项$ {\phi ^*}\left( {q,\tau } \right){\partial _\tau }\phi \left( {q,\tau } \right) $ 或者二次项$ {\left| {{\partial _\tau }\phi \left( {q,\tau } \right)} \right|^2} $ 。本文引入二次项$ \left|\partial_{\tau} \phi(q, \tau)\right|^{2} $ 以保证式(4)成为一个精确的相对论形式[15-18]:$$ \begin{array}{c} {\rm{L}}_{q}(T=0)= \left|\partial_{\tau} \phi(q, \tau)\right|^{2}+|\nabla \phi(q, \tau)|^{2}- \\ \dfrac{24 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} T_{c}^{2}|\phi(q, \tau)|^{2}+\dfrac{12 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} \dfrac{T_{c}^{2}}{\rho_{s}(0)} |\phi(q, \tau)|^{4} \end{array}$$ (5) 式(5)中没有任何的唯象参数,因此可由实验精确地检验。将式(5)对
$ \phi \left( {q,\tau } \right) $ 变分就得到相对论金兹堡−朗道方程[16]。按照Hertz的虚时量子场论框架,利用式(3)可以将式(5)的量子配分函数写为[15-18]:$$ Z(T=0)=\int\left[D \phi^{*}(q, \tau)\right]_{\varLambda } \int[D \phi(q, \tau)]_{\varLambda } e^{-\int {\rm{d}} \tau\int {\rm{d}}^{D} q{L_{q}}(T=0)} $$ (6) 式(6)是相对论金兹堡−朗道方程的虚时量子场论形式 [15]。下面利用它推导出文献[8]在实验上所发现的反常两段标度和本文所推测的关于零温相干长度
$ \xi \left( 0 \right) $ 与相变温度$ {T_c} $ 之间的两段标度。2.
$\; {\rho _s}\left( 0 \right) $ 与$ {T_c} $ 的两段标度关系首先利用式(6)推导出文献[8]在实验上所发现的反常两段标度,为此令
$ {\left| {\phi \left( {q,\tau } \right)} \right|^2} $ 和$ {\left| {\phi \left( {q,\tau } \right)} \right|^4} $ 前面的系数分别为$ {\lambda _2}\left( {{T_c}} \right) $ 和$ {\lambda _4}\left( {{T_c}} \right) $ ,由式(5)推出:$$ \lambda_{2}\left(T_{c}\right)=-\frac{24 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} T_{c}^{2} $$ (7) $$ \lambda_{4}\left(T_{c}\right)=\frac{12 {\text{π}}^{2} m_{e}}{7 \zeta(3) \varepsilon_{F}} \frac{T_{c}^{2}}{\rho_{s}(0)} $$ (8) 对处于
$ T = 0 $ 的过掺杂铜氧化物超导(此时热涨落被忽略不计),$ {T_c} = 0 $ 是一个可能的量子临界点,因此预期当$ {T_c} $ 趋于0时,量子涨落会被放大以至于平均场近似被破坏。按照重整化群的程序,假设波长大于$ {{2{\text{π}}} \mathord{\left/ {\vphantom {{2{\text{π}} } \Lambda }} \right. } \varLambda } $ 的量子涨落不能被平均掉[28-29],因此$ {\lambda _2}\left( {{T_c}} \right) $ 和$ {\lambda _4}\left( {{T_c}} \right) $ 应当收到来自这些尺度的量子涨落的高阶修正。为此,将重整化群程序运用到量子配分函数式(6),在单圈费曼图修正下可以得到重整化群方程为[15]:$$ \begin{array}{c} \lambda_{2}^{\prime}(b)= \\ b^{2}[\lambda_{2}+4 \lambda_{4} \displaystyle\int_{-\infty}^{+\infty} \dfrac{{\rm{d}} \omega}{2 {\text{π}}} \displaystyle\int_{\varLambda / b}^{\varLambda} \dfrac{{\rm{d}}^{D} k}{(2 {\text{π}})^{D}}(\dfrac{1}{\omega^{2}+k^{2}+\lambda_{2}}-\dfrac{1}{\omega^{2}+k^{2}})] \end{array} $$ (9) $$ \begin{array}{c} \lambda_{4}^{\prime}(b)=\\ b^{4-D-z} \lambda_{4}[1-10 \lambda_{4} \displaystyle\int_{-\infty}^{+\infty} \dfrac{{\rm{d}} \omega}{2 {\text{π}}} \displaystyle\int_{\varLambda/ b}^{\varLambda} \dfrac{{\rm{d}}^{D} k}{(2 {\text{π}})^{D}}(\dfrac{1}{\omega^{2}+k^{2}+\lambda_{2}})^{2}] \end{array} $$ (10) 式中,
$ b $ 是标度变换的重标参数;$ {q'} = {b^{ - 1}}q $ ;$ {\tau '} = $ $ {b^{ - z}}\tau $ ;$ z = 1 $ 代表量子动力学指数。算出式(9)和式(10)中的积分可以得到[18]:$$ \lambda _2'(b) \approx {\lambda _2}{b^{2 - 4{{\hat \lambda }_4}}} $$ (11) $$ \hat \lambda _4'(b) \approx {\hat \lambda _4}{b^{4 - D - z - 10{{\hat \lambda }_4}}} $$ (12) 式中,
$\hat{\lambda}_{4}=\lambda_{4} \dfrac{S_{D} \varLambda^{D-3}}{4(2 {\text{π}})^{D}}$ ;$S_{D}=2 {\text{π}}^{D / 2} / \varGamma(D / 2)$ 。将
$ z = 1 $ 代入之后,式(11)和式(12)可以被写为微分方程形式[15, 18]:$$ \frac{{\rm{d}} \lambda_{2}(T_{c})}{{\rm{d}} \ln b}=\lambda_{2}(T_{c})(2-4 \hat{\lambda}_{4})+O(\hat{\lambda}_{4}^{2}) $$ (13) $$ \frac{{{\rm{d}}{{\hat \lambda }_4}}}{{{\rm{d}}\;{\rm{ln}}\;b}} = (3 - D){\hat \lambda _4} - 10\hat \lambda _4^2 + O(\hat \lambda _4^3) $$ (14) 其中,
$$ {\hat \lambda _4} = {\lambda _4}\left( {{T_c}} \right)\frac{{{{({\text π} )}^{\tfrac{D}{2}}}{\varLambda ^{D - 3}}}}{{2{{(2{\text π} )}^D}\varGamma (D/2)}} $$ (15) 利用式(13)、式(14)和式(15)很容易得到非平凡不动点:
$$ \left\{\begin{array}{l} \lambda_{2}\left(T_{c}\right) \approx 0 \\ \lambda_{4}\left(T_{c}\right) \approx \dfrac{3-D}{10} \dfrac{2(2 {\text{π}})^{D} \varGamma(D / 2)}{({\text{π}})^{\tfrac{D}{2}} \varLambda^{D-3}} \end{array}\right. $$ (16) 已知
$ {\lambda _2}\left( {{T_c}} \right) $ 和$ {\lambda _4}\left( {{T_c}} \right) $ 被式(7)和式(8)定义,将它们代入式(16),则有:$$ \left\{\begin{array}{l} T_{c} \approx 0 \\ T_{c} \approx \gamma(D) \sqrt{\rho_{s}(0)} \end{array}\right. $$ (17) 其中,
$$ \gamma(D)=\sqrt{(3-D) \varLambda^{3-D} \frac{7(2 {\text{π}})^{D} \varGamma(D / 2) \zeta(3) \varepsilon_{F}}{60({\text{π}})^{\tfrac{D}{2}+2} m_{e}}} $$ (18) 令
$ {T_Q}\left( D \right) $ 代表一个充分低的温度,则可以用$ {T_c} \leqslant {T_Q}\left( D \right) $ 代替$ {T_c} \approx 0 $ 。这样,式(17)可写为等价形式:$$ \left\{\begin{array}{l} T_{c}=\gamma(D) \sqrt{\rho_{s}(0)} \\ T_{c} \leqslant T_{Q}(D) \end{array}\right. $$ (19) 式(19)的物理意义是:当相变温度
$ {T_c} $ 小于$ {T_Q}\left( D \right) $ 时,量子涨落被放大以至于平均场近似无效,此时$ {T_c} $ 和$ {\rho _s}\left( 0 \right) $ 按照亚线性关系同方向变化。为了推导出
$ {T_Q}\left( D \right) $ 的具体函数形式,需要找到一个估计量子涨落幅度的物理量。众所周知,在朗道的二级相变平均场理论中,经典金兹堡数$ {G_i} $ 被用于估计热涨落的幅度,从而判断平均场近似的有效范围。本文在虚时量子场论的框架中将经典金兹堡数$ {G_i} $ 推广为量子金兹堡数[17]:$$ e^{Q}(D)=\frac{\left|\int_{0}^{+\infty} \mathrm{d} \tau \int \mathrm{d}^{D} q G(q, \tau)\right|}{\int_{0}^{+\infty} \mathrm{d} \tau \int \mathrm{d}^{D} q\phi^* (q, \tau) \phi(q, \tau)} $$ (20) 式中,
$ G\left( {q,\tau } \right) $ 表示虚时格林函数,定义为[17]:$$ \begin{array}{*{20}{c}} {G\left( {q - {q^\prime },\tau - {\tau ^\prime }} \right) = }\\ {\left\langle {[\phi (q,\tau ) - \langle \phi (q,\tau )\rangle ][{\phi ^*}({q^\prime },{\tau ^\prime }) - \left\langle {{\phi ^*}({q^\prime },{\tau ^\prime })} \right\rangle ]} \right\rangle } \end{array} $$ (21) 显然,当
$ \phi \left( {q,\tau } \right) $ 独立于虚时间$ \tau $ 时,量子金兹堡数$ {e^Q}\left( D \right) $ 就变成经典金兹堡数$ {G_i} $ :容易验证当$ \phi \left( {q,\tau } \right) = \phi \left( q \right) $ 时,有:$$ {e^Q}\left( D \right) = \frac{{\left| {\int {{{\rm{d}}^D}q} G\left( q \right)} \right|}}{{\int {{{\rm{d}}^D}q} {\phi ^{\text{*}}}\left( q \right)\phi \left( q \right)}} = {G_i} $$ 根据金兹堡判据的基本精神,当且仅当金兹堡数远小于1,平均场近似有效。将其推广到量子涨落的情形,即有[17]:
$$ e^{Q}(D)<<1 $$ (22) 利用式(6)和量子金兹堡判据(22),已经证明平均场近似被破坏的条件为[17]:
$$ T_{Q}(D) \leqslant \xi^{2-D} \gamma(D)^{2} $$ (23) 式中,
$ \xi $ 代表超导体的相干长度。对于二维超导薄膜(
$ D = 2 $ ),式(23)给出$ {T_Q}\left( 2 \right) \leqslant \gamma {\left( 2 \right)^2} $ 。而对于$ D = 3 $ 的情形,式(23)结合式(18)则给出$ T_{Q}(3) \leqslant 0 $ ,这意味着对于三维系统平均场近似总是成立的,即$ D = 3 $ 是系统的上临界维度[15, 18]。当平均场近似有效的时候,已知
$ {T_c} $ 和$ {\rho _s}\left( 0 \right) $ 满足著名的 Homes定律[10-11]:$ {T_c} \propto {\rho _s}\left( 0 \right) $ 。综合式(18)、式(19)、式(23)以及Homes定律,在零温附近的过掺杂超导薄膜($ D = 2 $ )中的$ {T_c} $ 和$ {\rho _s}\left( 0 \right) $ 应当服从两段标度[17]:$$ \left\{\begin{array}{ll} T_{c}=\alpha \rho_s(0)+T_{0} \;&\; T_{c} \geqslant T_{M} \approx \dfrac{T_{0}}{1-\alpha} \\ T_{c}=\gamma(2) \sqrt{\rho_s(0)}\; &\; T_{c} \leqslant T_{Q} \approx \gamma(2)^{2} \end{array}\right. $$ (24) 式中,
$\gamma \left( 2 \right) = \sqrt {\dfrac{{7\zeta \left( 3 \right){\varepsilon _F}}}{{15{\text{π}} a{m_e}}}}$ 。式中,平均场近似有效的条件
$ {T_c} \geqslant {T_M} \approx {{T_0}} / {\left( {1 - \alpha } \right)} $ 由式(22)导出[17]。为了验证式(24)的有效性,将LSCO的实验数据[8]$ a \approx 3.8 \times {10^{ - 10}}m $ ,$ \alpha \approx 0.37 $ ,$ T_{0} \approx $ $ 7\; {\rm{K}} $ 以及[30]$ {\varepsilon _F}(x \approx 0.2) \approx 8.75\;{\rm{eV}} $ 代入式(24)中,从而得到如下理论值[16-17]:$$ \gamma(2) \approx 4.29 \;{\rm{K}}^{1 / 2} $$ (25) $$ T_{M} \approx 11 \mathrm{~K} $$ (26) $$ T_{Q} \approx 17 \mathrm{~K} $$ (27) 将这些理论值与文献[8]在实验上所发现的反常两段标度进行对比,3个理论值与实验测量值吻合良好,这是对相对论金兹堡−朗道方程(式(5))的有力支持[31]。
此外,
$ {T_Q} $ 与$ {T_M} $ 之间的差异表示两段标度被不光滑的连接,这已经被实验数据所证实,如图1所示,其中直线代表理论得到的线性标度,曲线代表理论得到的亚线性标度,空心圆圈代表实验数据[8]。3.
$ \xi \left( 0 \right) $ 与$ {T_c} $ 的两段标度关系以及讨论与热涨落导致关联长度(相干长度)在临界点发散一样,预期超导中的相干长度在量子临界点也是发散的。如式(4)指出,
$ {\left| {\phi \left( 0 \right)} \right|^2} $ 前面的系数不再是线性项$ \left(T-T_{c}\right) $ ,而是$ {T_c} $ 的二次项,这暗示在绝对零度附近,超导中的相干长度与相变温度$ {T_c} $ 之间标度关系的量子临界指数应当比对应的经典热临界指数要大一倍。为了证明这一点,利用式(11),有:$$b \approx {\left( {\lambda _2'(b)/{\lambda _2}} \right)^{1/\left( {2 - 4{{\hat \lambda }_4}} \right)}} $$ (28) 对于
$ b > > 1 $ 的情形,可选择参数$ b $ 使得$ {\lambda }_{2}'\left(b\right)= $ $ 常数 $ 。这样,超导的零温相干长度$ \xi \left( 0 \right) $ 应当趋于以下形式[18, 27]:$$\xi (0) \propto b \propto {\left( {1/{\lambda _2}} \right)^{1/\left( {2 - 4{{\hat \lambda }_4}} \right)}}$$ (29) 将式(7)代入式(29)得到:
$$ \xi(0) \propto T_{c}^{-\sigma} $$ (30) 其中,
$$ \sigma=1 /(1-2 \hat{\lambda}_{4}) $$ (31) 式(14)给出单圈费曼图修正下的不动点
$ \hat{\lambda}_{4} \approx $ $ (3-D) / 10 $ ,将其代入式(31)得到$ \sigma \approx 1+(3-D) / 5 $ 。如果考虑费曼图的二圈修正,那么式(31)可被修正为[18]:$$ \sigma \approx 1+\frac{1}{5}(3-D)+\frac{11}{100}(3-D)^{2} $$ (32) 对于二维超导薄膜
$ D = 2 $ ,式(32)预言$ \sigma \approx 1.31 $ 。此外,式(32)暗示平均场理论预言$ \sigma = 1 $ ,这与文献[17]利用平均场理论得到的结果一致。如果要考虑费曼图三圈以上的修正,那么只需注意到量子临界指数$ \sigma $ 的理论值是Wilson热关联长度临界指数的2倍[18]。考虑到三圈以上的费曼图,目前已有文献对于Wilson热关联长度临界指数的计算结果是$ 0.6703 \pm 0.0015 $ [32]。因此,当考虑三圈以上的费曼图贡献时,应当有$ \sigma \approx 1.34 $ 。与式(24)一样,费曼图的高阶修正仅当$ T_{c} \leqslant T_{Q} $ 时才有效。所以,应当预期零温相干长度$ \xi \left( 0 \right) $ 和相变温度$ {T_c} $ 也服从两段标度:$$ \left\{ {\begin{array}{*{20}{l}} {\xi (0) \propto T_c^{ - 1}}\;&\;{{T_c} \geqslant {T_M} \approx \frac{{{T_0}}}{{1 - \alpha }}}\\ {\xi (0) \propto T_c^{ - 1.34}}\;&\;{{T_c} \leqslant {T_Q} \approx \gamma {{(2)}^2}} \end{array}} \right.$$ (33) 式(33)暗示,当
$ T_{c} \leqslant \min \left\{T_{M}, T_{Q}\right\} $ 时,可以观测到精确的反常标度$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ ,而当$ {T_c} \geqslant {\text{max}}\left\{ {{T_M},{T_Q}} \right\} $ 时可以观测到精确的标度$ \xi \left( 0 \right) \propto T_c^{ - 1} $ 。两段标度式(33)是本文的核心理论结果,它给出一个新的理论推测,有待于实验检验。式(24)和式(33)暗示两段标度行为应当是过掺杂超导材料在绝对零度附近的一个普适现象。
$ T = {T_c} $ 是一个临界点,当物理系统的温度$ T $ 处于$ {T_c} $ 附近时,涨落应当被放大,其中既有热涨落也有量子涨落。当$ T $ 充分大时,热涨落足以压倒量子涨落,而在$ T = 0 $ 附近,热涨落则可以被忽略不计,从而量子涨落开始显现出来。因此,当超导材料处于$ T = 0 $ 附近时,热涨落被忽略掉,由于$ {T_c} = T = 0 $ 是一个临界点,所以当$ {T_c} $ 趋于0时,该系统将处于临界点$ T_{c}=0 $ 附近,意味着涨落被放大。但此时热涨落的影响可以被忽略,所以只有量子涨落被放大,而量子涨落的放大导致平均场近似不再有效。这就是当$ {T_c} $ 小于特征温标$ {\text{min}}\left\{ {{T_M},{T_Q}} \right\} $ 时,处于绝对零度附近的过掺杂超导材料会呈现量子临界现象的原因,该现象反映为式(24)中的$ {T_c} \propto \sqrt {{\rho _s}\left( 0 \right)} $ 以及式(33)中的$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ 。而当$ {T_c} $ 大于特征温标$ {\text{max}}\left\{ {{T_M},{T_Q}} \right\} $ 时,该零温系统因而得以远离临界点$ T_{c}=0 $ ,量子涨落处于正常幅度范围,所以平均场近似有效,这反映为式(24)中的$ {T_c} \propto {\rho _s}\left( 0 \right) $ 以及式(33)中的$ \xi \left( 0 \right) \propto T_c^{ - 1} $ 。以上讨论暗示可以通过掺杂铜氧化物超导薄膜使得$ {T_c} $ 小于特征温标$ {\text{min}}\left\{ {{T_M},{T_Q}} \right\} $ ,将这样的过掺杂材料降温到绝对零度附近,可高效地激发量子涨落,从而是一种构造量子退火计算机的潜在材料。最后,简单讨论一下式(5)中虚时间
$ \tau $ 的意义。量子场论不寻常的性质之一是,当时间变量$ t $ 成为虚时间$ \tau $ 时,它在形式上就简化成了统计力学,这个性质在数学上被称为“维克旋转”,可用于简化量子场论中的一些计算。比较式(3)和式(6)可以看到,虚时间$ \tau $ 本质上就是温度$ T $ 的倒数,或者按照文献[33]的说法,温度等价于周期性虚时间(cyclic imaginary time)。为什么温度与虚时间会有这个神秘的关系?这仍旧是物理学中的一个未解之谜,它背后可能涉及到某些未被理解的深刻物理原理[33-34]。为了理解温度与虚时间的关系,文献[35-38]基于Tomita-Takesaki定理提出了“热时间假说(thermal time hypothesis)”,这个假说认为物理系统中的时间本质上是一个演生(涌现)的变量,它可能源于量子力学中的不对易性[36]。如当一个物理系统处于绝对零度$ T = 0 $ 时,原子与分子都应该处于静止,没有运动谈论时间是没有意义的。但由于海森堡不确定性原理的作用,原子与分子不可能处于静止(位置变化为0),否则它们的动量变化将趋于无穷大。这意味着当温度趋于绝对零度$ T = 0 $ 时,物理系统将自发演生(涌现)出时间(去描述量子运动)。从式(6)看出这个演生时间其实就是虚时间$ \tau $ 。尽管“热时间假说”被提出,但之前的文献并没有任何物理系统会出现“演生时间”的精确相对论方程。这使得“热时间假说”难以得到验证——即如何确保“演生时间”就是物理时间。因此,如果本文的相对论式(5)能够得到验证,那么可能会是对“热时间假说”的一个潜在支持。但需要提及的是,即使相对论式(5)被实验证实,它所描述的物理背景也是“虚时空”——即库珀电子对在虚时空中存在精确的相对论方程。这与单电子的相对论方程(狄拉克方程)不同,后者描述的是现实的物理时空。
4. 结 束 语
本文通过将统计物理配分函数中温度T的倒数作为第4维“虚时间”,将绝对零度处的金兹堡−朗道方程推广为相对论形式,从而建立起描述绝对零度附近的超导体的虚时量子场论。基于相对论金兹堡−朗道方程的虚时量子场论框架(式(6)),本文显示最近被文献[8]在LSCO单晶薄膜中观测到的
$ {\rho _s}\left( 0 \right) $ 与$ {T_c} $ 之间的反常两段标度可以被精确地推导出。其中,当相变温度$ {T_c} $ 小于特征温标$ {\text{min}}\left\{ {{T_M},{T_Q}} \right\} $ 时,$ {\rho _s}\left( 0 \right) $ 与$ {T_c} $ 遵从亚线性标度$ {T_c} \propto \sqrt {{\rho _s}\left( 0 \right)} $ ,这是一种量子临界现象;而当$ {T_c} $ 大于特征温标$ {\text{max}}\left\{ {{T_M},{T_Q}} \right\} $ 时,$ {\rho _s}\left( 0 \right) $ 与$ {T_c} $ 遵从Homes定律$ {T_c} \propto {\rho _s}\left( 0 \right) $ ,这是平均场理论的结果。不仅$ {\rho _s}\left( 0 \right) $ 与$ {T_c} $ 会服从两段标度,本文基于相对论金兹堡−朗道方程的虚时量子场论进一步预言零温相干长度$ \xi(0) $ 与相变温度$ {T_c} $ 也基于同样的物理机理而服从另一个两段标度:当相变温度$ {T_c} $ 小于特征温标$ {\text{min}}\left\{ {{T_M},{T_Q}} \right\} $ 时,$ \xi(0) $ 与$ {T_c} $ 遵从标度$ \xi \left( 0 \right) \propto T_c^{ - 1.34} $ ;而当$ {T_c} $ 大于特征温标$ {\text{max}}\left\{ {{T_M},{T_Q}} \right\} $ 时,$ \xi(0) $ 与$ {T_c} $ 遵从标度$ \xi \left( 0 \right) \propto T_c^{ - 1} $ 。希望国内感兴趣的实验组可以通过调查绝对零度附近的过掺杂铜氧化物超导薄膜去精确检验
$ \xi(0) $ 与$ {T_c} $ 之间的两段标度,以确证相对论金兹堡−朗道方程(式(5))的有效性。 -
[1] HERTZ J A. Quantum critical phenomena[J]. Phys Rev B, 1976, 14(3): 1165. DOI: 10.1103/PhysRevB.14.1165
[2] MILLIS A J. Effect of a nonzero temperature on quantum critical points in itinerant fermion systems[J]. Phys Rev B, 1993, 48(10): 7183. DOI: 10.1103/PhysRevB.48.7183
[3] LIANG R X, BONN D A, HARDY W N, et al. Lower critical field and superfluid density of highly underdoped
$ {\text{YB}}{{\text{a}}_2}{\text{C}}{{\text{u}}_3}{{\text{O}}_{6 + x}} $ single crystals[J]. Phys Rev Lett, 2005, 94(11): 117001. DOI: 10.1103/PhysRevLett.94.117001[4] ZUEV Y, KIM M S, LEMBERGER T R. Correlation between superfluid density and
$ {T_c} $ of Underdoped$ {\text{YB}}{{\text{a}}_2}{\text{C}}{{\text{u}}_3}{{\text{O}}_{6 + x}} $ Near the superconductor-insulator transition[J]. Phys Rev Lett, 2005, 95(13): 137002. DOI: 10.1103/PhysRevLett.95.137002[5] HETEL I, LEMBERGER T R, RANDERIA M. Quantum critical behaviour in the superfluid density of strongly underdoped ultrathin copper oxide films[J]. Nature Physics, 2007, 3: 700-702. DOI: 10.1038/nphys707
[6] TAO Y. Scaling laws for thin films near the superconducting-to-insulatin transition[J]. Scientific Reports, 2016, 6: 23863. DOI: 10.1038/srep23863
[7] 张若舟, 秦明阳, 张露, 等. 超导薄膜磁场穿透深度的双线圈互感测量[J]. 物理学报, 2020, 69(4): 047401. DOI: 10.7498/aps.69.20191758 ZHANG R Z, QIN M Y, ZHANG L, et al. Measurement of magnetic penetration depth in superconducting films by two-coil mutual inductance technique[J]. Acta Physica Sinica, 2020, 69(4): 047401. DOI: 10.7498/aps.69.20191758
[8] BOŽOVIĆ I, HE X, WU J, et al. Dependence of the criticaltemperature in overdoped copper oxides on superfluid density[J]. Nature, 2016, 536: 309-311. DOI: 10.1038/nature19061
[9] HOMES C C, DORDEVIC S V, VALLA T, et al. Scaling of the superfluid density in high-temperature superconductors[J]. Phys Rev B, 2005, 72(13): 134517. DOI: 10.1103/PhysRevB.72.134517
[10] KOGAN V G. Homes scaling and BCS[J]. Phys Rev B, 2013, 87(22): 220507(R). DOI: 10.1103/PhysRevB.87.220507
[11] ABRIKOSOV A A, GORKOV L P, DZYALOSHINSKII I E. Methods of quantum field theory in statistical physics[M]. NJ: Prentice-Hall, 1963.
[12] KHODEL V A, CLARK J W, ZVEREV M V. Impact of electron-electron interactions on the superfluid density of dirty superconductors[J]. Phys Rev B, 2019, 99(18): 184503. DOI: 10.1103/PhysRevB.99.184503
[13] BOŽOVIĆ I, HE X, WU J, et al. The vanishing superfluid density in cuprates-and why it matters[J]. Journal of Superconductivity and Novel Magnetism, 2018, 31(9): 2683-2690. DOI: 10.1007/s10948-018-4792-7
[14] BOŽOVIĆ I, BOLLINGER A T, WU J, et al. Can high- superconductivity in cuprates be explained by the conventional BCS theory?[J]. Low Temperature Physics, 2018, 44(6): 519-527. DOI: 10.1063/1.5037554
[15] TAO Y. BCS quantum critical phenomena[J]. Europhysics Letters, 2017, 118(5): 57007. DOI: 10.1209/0295-5075/118/57007
[16] TAO Y. Parabolic scaling in overdoped cuprate films[J]. Journal of Superconductivity and Novel Magnetism, 2019, 32(12): 3773-3777. DOI: 10.1007/s10948-019-05179-5
[17] TAO Y. Parabolic scaling in overdoped cuprate: A statistical field theory approach[J]. Journal of Superconductivity and Novel Magnetism, 2020, 33(5): 1329-1337. DOI: 10.1007/s10948-019-05337-9
[18] TAO Y. Relativistic Ginzburg–Landau equation: An investigation for overdoped cuprate films[J]. Physics Letters A, 2020, 384(26): 126636. DOI: 10.1016/j.physleta.2020.126636
[19] LEE-HONE N R, DODG J S E, BROUN D M. Erratum: Disorder and superfluid density in overdoped cuprate superconductors[J]. Phys Rev B, 2017, 96(2): 024501. DOI: 10.1103/PhysRevB.96.024501
[20] HERMAN F, HLUBINA R. Thermodynamic properties of Dynes superconductors[J]. Phys Rev B, 2018, 97(1): 014517. DOI: 10.1103/PhysRevB.97.014517
[21] GOUTERAUX B, MEFFORD E. Normal charge densities in quantum critical superfluids[J]. Phys Rev Lett, 2020, 124(16): 161604. DOI: 10.1103/PhysRevLett.124.161604
[22] KADOWAKI T, NISHIMORI H. Quantum annealing in the transverse Ising model[J]. Phys Rev E, 1998, 58(5): 5355. DOI: 10.1103/PhysRevE.58.5355
[23] BIAMONTE J, WITTEK P, PANCOTTI N, et al. Quantum machine learning[J]. Nature, 2017, 549: 195-202. DOI: 10.1038/nature23474
[24] HU F, WANG B N, WANG N, et al. Quantum machine learning with D-wave quantum computer[J]. Quantum Engineering, 2019, 1(2): e12
[25] TAO Y. Swarm intelligence in humans: A perspective of emergent evolution[J]. Physica A, 2018, 502: 436-446. DOI: 10.1016/j.physa.2018.02.120
[26] TAO Y. Self-referential Boltzmann machine[J]. Physica A, 2020, 545: 123775. DOI: 10.1016/j.physa.2019.123775
[27] HERBUT I. An modern approach to critical phenomena[M]. Cambridge: Cambridge University Press, 2007: 168-169
[28] WILSON K G, KOGUT J. The renormalization group and the expansion[J]. Physics Reports, 1974, 12(2): 75-199. DOI: 10.1016/0370-1573(74)90023-4
[29] WILSON K G. The renormalization group and critical phenomena[J]. Rev Mod Phys, 1983, 55(3): 583. DOI: 10.1103/RevModPhys.55.583
[30] KAMIMURA H, USHIO H. Energy bands, fermi surface and density of states in the superconducting state of
$ {\text{L}}{{\text{a}}_{2 - x}}{\text{S}}{{\text{r}}_x}{\text{Cu}}{{\text{O}}_4} $ [J]. Solid State Communications, 1994, 91(2): 97-100. DOI: 10.1016/0038-1098(94)90261-5[31] HERRERA C, FRANKLIN J, BOŽOVIĆ I, et al. Scanning SQUID characterization of extremely overdoped
$ {\text{L}}{{\text{a}}_{2 - x}}{\text{S}}{{\text{r}}_x}{\text{Cu}}{{\text{O}}_4} $ [J]. Phys Rev B, 2021, 103(2): 024528. DOI: 10.1103/PhysRevB.103.024528[32] GUIDA R, ZINN-JUSTIN J. Critical exponents of the N-vector model[J]. Journal of Physics A: Mathematical and General, 1998, 31(40): 8103. DOI: 10.1088/0305-4470/31/40/006
[33] ZEE A. Quantum field theory in a nutshell (Second Edition)[M]. NJ: Princeton University Press, 2010.
[34] 黄克孙. 大自然的基本力: 规范场的故事[M]. 上海: 上海世纪出版集团有限公司, 2009. HUANG K S. Fundamental forces of nature: The story of gauge fields[M]. Shanghai: Shanghai Century Publishing Group Co. Ltd, 2009.
[35] ROVELLI C. Statistical mechanics of gravity and the thermodynamical origin of time[J]. Classical and Quantum Gravity, 1993, 10(8): 1549. DOI: 10.1088/0264-9381/10/8/015
[36] CONNES A, ROVELLI C. Von Neumann algebra automorphisms and time-thermodynamics relation in generally covariant quantum theories[J]. Classical and Quantum Gravity, 1994, 11(12): 2899. DOI: 10.1088/0264-9381/11/12/007
[37] ROVELLI C. Forget time[J]. Foundations of Physics, 2011, 41(9): 1475. DOI: 10.1007/s10701-011-9561-4
[38] TANAKA S. Appearance of thermal time[J]. Foundations of Physics, 2021, 51(2): 34. DOI: 10.1007/s10701-021-00445-w
-
期刊类型引用(0)
其他类型引用(1)

 ISSN
ISSN 












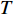
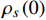
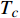

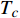
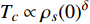

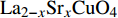
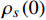
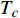
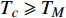
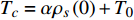
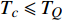
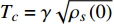
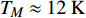
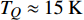
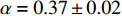
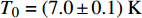
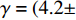
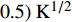
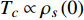
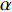
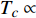
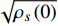
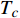

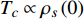
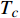
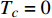
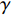
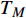
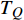
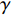
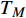
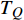

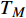
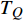
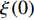

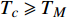
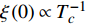
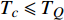

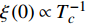
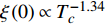
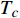

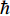
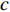
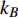
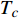
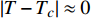
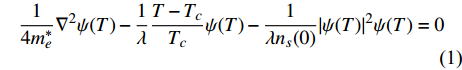
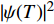
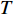
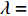

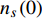
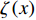
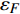



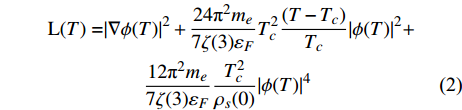

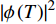
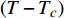
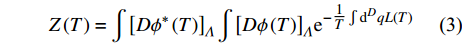

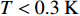


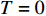
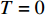
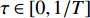

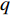
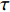
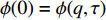
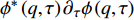


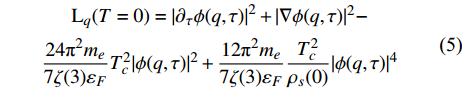
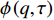


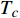
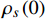
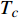

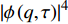
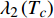
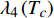

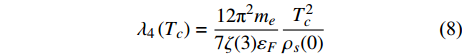


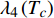
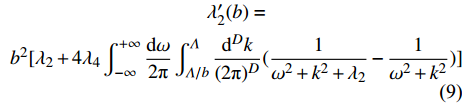
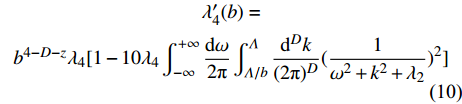
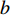
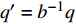
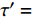

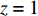
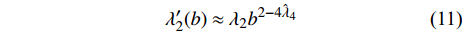
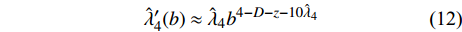

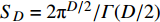
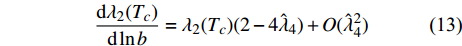
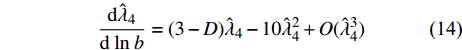
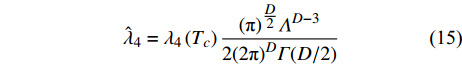
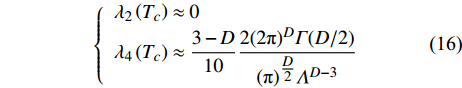

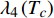
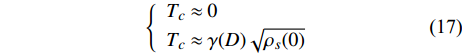
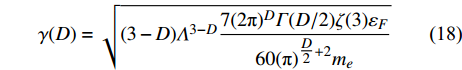
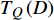
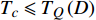
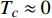
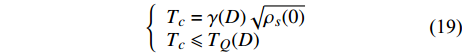



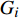
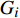
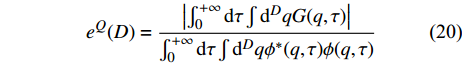
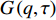
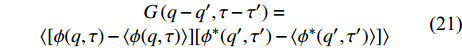
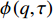
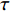
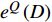
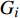
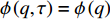
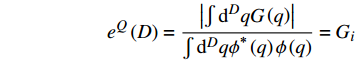
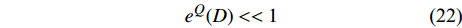
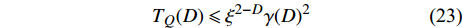
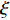
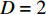
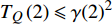
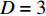
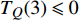
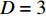
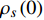
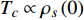

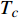
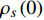
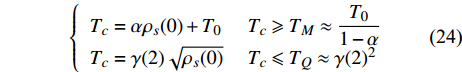
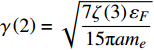
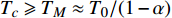
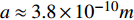
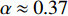
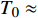
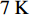
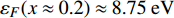
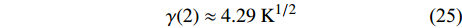
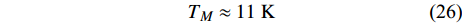
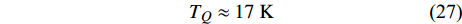
 下载:
下载: