Study on Integrated Radar and Communication Signal Based on Chirp-rate Modulation
-
摘要: 雷达通信一体化可有效提高电子系统的资源共享,是实现电子装备多功能综合一体化的一个重要方向。本文根据Chirp信号的调频率与分数阶傅里叶变换的阶数之间的关系,提出了一种基于Chirp信号调频率的雷达通信共享波形,固定调频率的主载波实现雷达功能,副载波由通信码元键控得到调频率从而实现通信信息调制;主载波与副载波的叠加形式使此共享信号能在不影响雷达性能的前提下实现单脉冲多比特的数据传输,而且利用不同阶数的分数阶傅里叶变换的解调过程具有多普勒稳健性。Abstract: Integrated radar and communication system can make full use of radar equipment and play an important role in achievement of multi-functional integration of electronic equipment. A kind of integrated radar and communication signal is proposed based on the relationship between chirp-rate of chirp signal and the order of fractional Fourier transform. Its main carrier adopts the unique chirp signal to implement radar function, while communication information is modulated by the subcarrier with communication code keying chirp-rate chirp signal. The superposition of the main carrier and the subcarrier enables the signal to transmit multi-binary information by single signal without degrading radar's performance. Finally, simulations demonstrate that the proposed signal has an advantage of high robustness.
-
为在信息化作战中,体现出“信息化优势”,要求武器的发展和使用具有系统化趋势,使各种武器平台通过电子信息渠道实现跨领域、超距离的实时合作。同时,为适应现代化电子战环境的要求,武器平台需要装备数量众多的电子设备,如雷达、通信设备等[1],但这些设备占据电子设备中的宝贵空间、增加其载荷、恶化周围电磁环境,使得航电设备综合性能受到影响,而雷达和通信作为作战平台的基本组成单位,如果能在雷达设备上增加通信功能,使其以一个系统运行,将会大大提高电子设备的综合利用率。
近几年,国内外在雷达设备上增加通信功能开展了广泛研究。美国海军率先在2005年完成了先进多功能射频概念平台的初步报告[2],表明多功能综合一体化已进入实验化筹备阶段。2006年,Northrop Grumman公司在E-8C联合监视和攻击雷达系统上对雷达通信一体化进行了研究,采用脉冲体制,并在频率上将雷达信号和通信信号进行区分,经测试,在相距140 km,DBPSK调制下,传输速率达到1.5 Mb×s-1[3]。中国电子科学研究院在2009年到2011年,联合中电38所、北京理工大学等多家单位,研制开发了雷达/通信一体化窄带数字阵列实验系统,其通信速率可达到300 kb·s-1[4]。
目前研究主要集中在雷达通信一体化波形设计,现有的一体化波形主要分为两大类:一类是波形共用技术,按照时分[5]、频分[6]、码分[7]等方式对波形共用;另一类是波形共享技术,一是直接利用通信波形实现对目标的探测[8],二是通过对雷达波形改造,使通信信息以差异性的形式体现在雷达波形上,文献[9]研究了通过调制Chirp信号的初始频率实现雷达通信一体化的方法;文献[10]研究了LFM信号与通信MSK调制方式相结合的设计方法;文献[11]研究了基于Chirp扩频的一体化方式。但这些设计方法一方面未考虑到雷达信号处理的“不变”与通信传输数据的“变”之间的矛盾,即雷达信号处理中为提升信噪比,需进行相参积累,要求脉冲间波形“不变”,使其具有较高相干性,而为进行通信传输,传输数据的随机性要求“变”;另一方面,目前研究的较多波形在存在多普勒频移的情况下,其通信性能会变差。针对以上问题,本文提出了一种基于Chirp信号的雷达通信一体化设计方法,其主载波实现雷达功能,副载波通过调制调频率实现通信信息调制,通过理论分析和仿真实验说明了本文的设计方法能在一定程度上实现雷达和通信一体化。
1. 调频率调制的共享Chirp信号设计
1.1 共享波形设计
线性调频信号(Chirp)的复包络形式为:
$$ s\left( t \right) = {\text{rect}}\left( {t/\tau } \right){{\text{e}}^{{\text{j}}\left( {2\pi {f_0}t + \pi \mu {t^2} + \varphi } \right)}} $$ (1) 式中,f0为中心频率;φ为初始相位;$\mu = B/\tau $为Chirp信号的调频率;τ时间内,瞬时频率变化范围为μτ,称为扫频带宽;B为信号带宽;rect(t/τ)为矩形脉冲函数,表示Chirp信号的持续时间,即脉宽:
$$ {\text{rect}}\left( {\frac{t}{\tau }} \right) = \left\{ \begin{gathered} 1\;\;\;-\tau /2 \leqslant t \leqslant \tau /2 \hfill \\ 0\;\;\;\;其他 \hfill \\ \end{gathered} \right. $$ (2) 基于Chirp信号的调频率与分数阶傅里叶变换特性的相互关系,设计利用不同的调频率携带通信码元信息的雷达通信共享波形[12]。考虑一组不同调频率的Chirp信号组$\left\{ {{s_k}\left( t \right)\left| {0 \leqslant k \leqslant {2^N} - 1} \right.} \right\} $,其表达式:
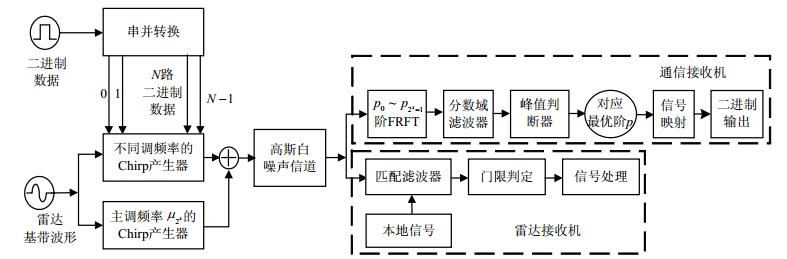
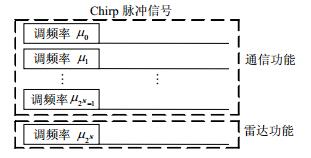
$$ {s_k}(t) = {\text{rect}}\left( {\frac{t}{\tau }} \right){{\text{e}}^{{\text{j}}(2{\text{ π }}{f_0}t + {\text{ π }}{\mu _k}{t^2})}}{\text{ }}0 \leqslant k \leqslant {2^N} - 1 $$ (3) 式中,${\mu _k} = {\mu _0} + k\Delta \mu $为第k个Chirp信号的调频率;Δμ为相邻调频率的间隔。将通信调制码元数据(N位)映射到不同调频率(2N个调频率)的Chirp信号序列中,单个Chirp信号可携带N的数据。而雷达为提高信噪比,需进行相干积累,要求一个CPI内各脉冲之间相关,因此采用某一固定调频率μ2N(与上述2N个调频率不同)的Chirp信号实现雷达目标测距、测速等功能,如图 1所示。最终共享信号为主、副载波Chirp信号叠加产生,主载波Chirp信号用做雷达功能,副载波为N位码元映射产生的Chirp信号用做通信功能,一个脉冲可发送N位码元信息。
雷达通信共享信号系统框图如图 2所示,在发射端,将串并转换后的N位二进制数据送入Chirp信号发生器中,对Chirp信号组键控,产生一个特定调频率的副载波Chirp信号,与固定调频率的主载波Chirp信号叠加组成发射信号,送入高斯白噪声信道。在雷达接收处理模块中,将接收到的回波与本地样本信号做匹配滤波,对其输出的相关信号做门限判定,最后进行雷达信号处理,从而判定目标的有无,得到目标的具体信息。在通信接收端,对接收信号采样后,依次进行${\mu _0} \sim {\mu _{{2^N} - 1}} $对应的${p_0} \sim {p_{{2^N} - 1}} $阶次的分数阶傅里叶变换,对变换后的数据进行门限判定,确定最优阶变换对应的阶次,再通过信号映射解出最优阶的调频率对应的二进制数据,最后对得到的二进制数据进行并串变换,解调输出通信码元数据。
1.2 Chirp信号的分数阶傅里叶变换
本文利用Chirp信号的调频率与其分数阶傅里叶变换之间的对应关系进行通信解调,首先对Chirp信号的分数阶傅里叶变换进行介绍。
对于信号x(t),其对应的FRFT的表达式为:
$$ \begin{gathered} {X_\alpha }(u){\text{F}}{f^p}[x(t)] = \\ \left\{ \begin{gathered} \sqrt {\frac{{1 -{\text{j}}\cot \alpha }}{{2\pi }}} {{\text{e}}^{{\text{j}}\frac{{{u^2}}}{2}\cot \alpha }}\int_{{\text{ }} -\infty }^{{\text{ }} + \infty } {x(t){{\text{e}}^{{\text{j}}\left( {\frac{{{t^2}}}{2}\cot \alpha -tu\csc \alpha } \right)}}} {\text{ }}\alpha \ne n\pi \hfill \\ x(u)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = 2n\pi \hfill \\ x( - u)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = (2n \pm 1)\pi \hfill \\ \end{gathered} \right. \\ \end{gathered} $$ (4) 式中,p为变换阶次;α=pπ/2;Fp[·]为FRFT的算子符号。将Chirp信号的复包络表达式代入式(4),调整简化后得到:
$$ \begin{gathered} {S_\alpha }\left( u \right) = A\sqrt {1 - {\text{jcot}}\alpha } \exp \left( {{\text{j}}\pi {u^2}\cot \alpha } \right) \times \hfill \\ \int_{ - \tau /2}^{\tau /2} {\exp \left( {{\text{j}}\pi \left( {\mu + \cot \alpha } \right){{\text{t}}^2} + {\text{j2}}\pi \left( {{f_0} - u\csc \alpha } \right){\text{t}}} \right){\text{d}}t} \hfill \\ \end{gathered} $$ (5) 当且仅当μ=-cotα时,
$$ \begin{gathered} {S_\alpha }(u) = A\sqrt {1- {\text{j}}\cot \alpha } exp({\text{j}}\pi {u^2}\cot \alpha ) \times \\ \frac{{\sin [\pi ({f_0}-u\csc \alpha )\tau]}}{{\pi ({f_0} -u\csc \alpha )}} \\ \end{gathered} $$ (6) 由调频率μ确定变换阶次后得到含Sa函数的表达式,分析其幅度谱特性,可以得到当f0=μcscα时,有峰值输出,幅度峰值的平方输出为:
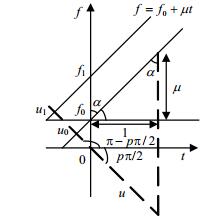
$$ {\left| {{S_\alpha }(u)} \right|^2} = \frac{{{A^2}{\tau ^2}}}{{\left| {\sin \alpha } \right|}} $$ (7) Chirp信号的时频坐标变化示意图如图 3所示,瞬时频率f=f0+μt。
由表达式与示意图可以得到,分数阶傅里叶变换的阶数和峰值位置分别可以表示为:
$$ \left\{ \begin{gathered} \mu = - \cot \alpha \hfill \\ {f_0} = u\csc \alpha \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} p = - 2{\text{arc cot}}\mu {\text{/}}\pi \hfill \\ u = - {f_0}\sin \left( {{\text{arc cot}}\mu } \right) \hfill \\ \end{gathered} \right. $$ (8) 分析得知,Chirp信号的调频率μ决定了分数阶傅里叶变换唯一的最优变换阶次pm,载频f0决定了在pm阶的分数阶傅里叶变换域上最优的能量聚集位置,即幅度峰值位置。对Chirp信号进行非最优阶FRFT变换时,分数阶傅里叶域谱不具有聚集性质。
1.3 多元正交波形
本文所设计共享信号采用主载波进行雷达探测,副载波调制调频率传输通信信息,在接收端需对回波信号进行分离,将主载波分离出来完成雷达探测功能,根据相关性可判断是否能将其分离,下面分析有不同调频率的Chirp信号之间的相关性。
设两个调频率不同的Chirp信号分别为:
$$ {s_1}(t) = {C_n}{\text{rect}}\left( {\frac{t}{{\tau '}}} \right){{\text{e}}^{{\text{j}}\pi {\mu _1}{t^2}}} $$ (9) $$ {s_2}(t) = {D_m}{\text{rect}}\left( {\frac{t}{{\tau '}}} \right){{\text{e}}^{{\text{j}}\pi {\mu _2}{t^2}}} $$ (10) 式中,Cn和Dm为不同编码序列;τ’为脉宽;μ1、μ2为对应的线形调频率。根据相关函数的定义,则s1(t)和s2(t)对应的互相关函数为:
$$ {\chi _{{s_1}, {s_2}}}(\tau, {f_d}) = \int_{{\text{ }}R} {{s_1}(t)s_2^*(t - \tau ){\text{d}}t} $$ (11) 将s1和s2的表达式代入上式,计算得:
$$ \begin{gathered} {\chi _{{s_1}, {s_2}}}(\tau, {f_d}) = {C_n}D_m^*\int_R {{\text{rect}}\left( {\frac{t}{{\tau '}}} \right){\text{rec}}{{\text{t}}^*}\left( {\frac{{t-\tau }}{{\tau '}}} \right)} \times \\ {{\text{e}}^{{\text{j}}\pi ({\mu _1}{t^2}-{\mu _2}{{(t-\tau )}^2})}}{\text{d}}t \\ \end{gathered} $$ (12) 分析上式得到:1)线形调频信号具有不同调频率μ1和μ2时,其相关性较低,即通过匹配滤波可将其分离;2)选择合适的编码序列Cn和Dm及编码长度可改善其正交性。
2. 共享波形参数设计
2.1 Chirp信号调频率设计
设计Chirp信号调频率主要涉及到两个方面,一是用作雷达的主载波调频率的确定,二是用作通信的副载波内调频率的确定。雷达主载波调频率决定了雷达信号可用的带宽,带宽决定了目标检测的分辨率,而根据正交性分析,可以用匹配滤波将主载波从共享信号中区分开来,副载波对主载波的雷达功能影响较小,为了使目标检测性能最优,设计主载波的调频率大于所有用于通信的调频率,使其带宽利用达到最大,得到较高分辨率。
通信副载波设计一组有等间隔调频率的Chirp信号组{μi},主要被两方面限制,一方面由于Chirp信号的时宽带宽积$B\tau = \mu {\tau ^2} $,对于固定的信号脉宽τ,μ越大Chirp信号占用的带宽越大,{μi}的最大取值被可用带宽所限制,为得到大的通信传输速率,需在可用带宽内尽可能设计多的μi;另一方面,{μi}一一对应N位二进制通信信息,其中相邻的μi和μi+1对应的两个最优分数阶傅里叶变换阶次pi和pi+1的间隔Δp决定了采用分数阶傅里叶变换进行解调时对相邻符号的区分度,即Δp决定了相邻符号间的干扰程度。根据Δp与μi、μi+1的关系:
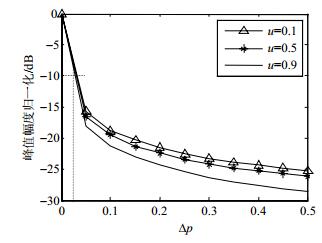
$$ \Delta p = 2\left| {{\text{arc cot}}{\mu _i} - {\text{arc cot}}{\mu _{i + 1}}} \right|/\pi $$ (13) 对Chirp信号进行非最优阶FRFT时,分数傅里叶域谱不具有聚集性质,而且随着变换阶次偏离p的程度Δp增大,FRFT的峰值明显下降。这由图 4验证,Chirp信号归一化的调频率分别为0.1、0.5、0.9[13],具有相同的脉宽,随Δp增大峰值幅度降低,若设定FRFT变换峰值幅度门限在-10 dB,则{μi}的设计要使得Δp至少为0.03。
2.2 通信解调的多普勒稳健性
雷达与目标或接收端之间不是彼此相对静止时,由于多普勒效应,接收到的信号就会存在多普勒频移fd,则接收Chirp信号形式将变为:
$$ \begin{gathered} s(t) = A\exp ({\text{j}}(2\pi {{f'}_0}t + \pi \mu {t^2} + \varphi )) \\ t \in [0, \tau], {\text{ }}{{f'}_0} = {f_0} + {f_d} \\ \end{gathered} $$ (14) 可以看出,多普勒频移fd会造成中心频率f0的变化,调频率μ不发生改变,随之变化的是分数阶傅里叶域上的峰值位置,此时的解调器输出峰值偏移量和幅度平方输出分别为:
$$ \Delta u = {f_d}\sin ({\text{arc}}\cot ( - \mu )) $$ (15) $$ {\left| {{S_\alpha }(u)} \right|^2} = \frac{{{A^2}}}{{{{\sin }^2}\alpha }} \times \frac{{{{\sin }^2}(\pi {f_d}\tau )}}{{{{(\pi {f_d})}^2}}} $$ (16) 在共享信号系统中,一般μ的数量级为1012~1014,sin(arc cot(-μ))的数量级为-1012~-1014,而fd一般不会超过2 kHz,故Δμ可以忽略不计。由于多普勒频移fd带来的幅度平方衰减系数为:
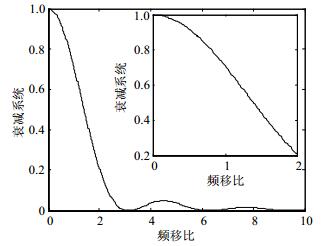
$$ \gamma = \frac{{{A^2}}}{{{{\sin }^2}\alpha }} \cdot \frac{{{{\sin }^2}\left( {\pi {f_d}\tau } \right)}}{{{{\left( {\pi {f_d}} \right)}^2}}}/\frac{{{A^2}{\tau ^2}}}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\left( {\pi {f_d}\tau } \right)}}{{{{\left( {\pi {f_d}\tau } \right)}^2}}} $$ (17) 由上式可以看出衰减系数只与多普勒频移fd和信号脉宽τ有关。定义频移比[14]为$\xi = \pi {f_d}\tau $,衰减系数与频移比的关系:
$$ \gamma = {\left[{\frac{{\sin (\xi )}}{\xi }} \right]^2} $$ (18) 由此画出衰减系数与频移比的关系如图 5所示,可以看出即使频移比达到0.5,峰值幅度衰减尚不到0.1,可以得知此多普勒频移不影响共享信号的FRFT解调阶数,说明了本文所设计的一体化波形对多普勒是稳健的。
3. 仿真分析
仿真实验中,设定二进制数据对16个不同调频率的Chirp信号进行键控调制,并根据设计要求设计仿真参数:载频fc=10 GHz,带宽B=100 MHz,脉冲重复周期PRI=10 μs,信号脉宽τ=1 μs,主载波Chirp信号调频率为μ2N=100 MHz/μs,副载波Chirp信号可选调频率为[10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85] MHz/μs,由二进制数据“0111”选择副载波μ=40 MHz/μs,目标相对距离与速度分别为700 m、200 m/s。
3.1 雷达仿真分析
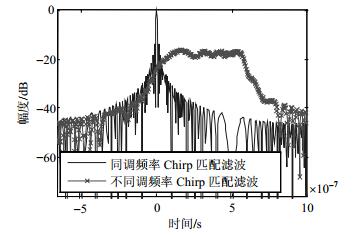
由图 2系统框图可知,雷达对目标的检测是通过回波信号与本地信号进行匹配滤波处理完成的,目标检测的性能可能会被发射脉冲中不同调频率的Chirp信号回波分量所影响。由于发射脉冲中被用作雷达目标检测的固定调频率μ2N的Chirp信号是已知的,反射回波中存在用作通信的Chirp信号的调频率分量可能为μi。图 6为同调频率与不同调频率的两Chirp信号的匹配滤波图,由图知,若回波中Chirp信号的调频率与参考信号的调频率不同,则相对幅度大约在-20 dB左右,对目标检测的影响可忽略,通过匹配滤波即可分离出主载波。所以,回波中存在的不同调频率的Chirp分量对目标的检测性能的影响可以忽略。这种调制方案可以在不影响雷达性能的情况下,完成通信码元数据的传输。
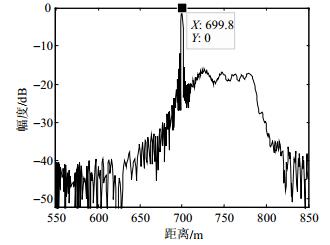
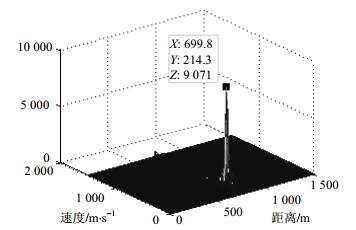
为了说明用本文所设计的共享信号符合雷达处理过程相干积累的要求,对一个CPI内的各脉冲的脉压输出结果之间的相关性进行分析,得到它们之间的互相关系数均为1,满足要求,故此共享信号只需要一个匹配滤波器进行目标检测处理。图 7为回波匹配脉压结果,图 8为MTD处理结果。
3.2 通信仿真分析
根据不同调频率的Chirp信号相应的最优分数阶傅里叶变换阶次不同,设定一个信号调频率的集合{μi},在发射端利用调制信息串并转换依次对各个脉冲副载波μi进行键控。在接收端将接收到的信号进行一系列{μi}对应阶次的分数阶傅里叶变换,并进行判决,得到对应的最优阶次,从而解调出调制码元数据。
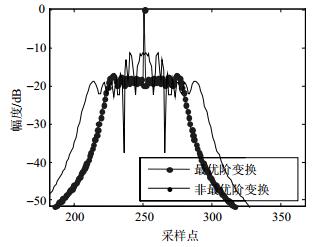
解调端对接收信号进行一系列预定阶次的FRFT变换,以最优阶变换幅度峰值进行归一化,结果如图 9,当进行最优阶FRFT变换时在其幅度谱上输出峰值,当进行其他阶次FRFT变换时,其幅度谱上无峰值输出,由此得到接收信号FRFT变换的最优阶,从而解得通信调制信息。
通信性能的一个重要指标是通信速率,通信速率主要由PRF、{μi}个数决定,通信速率可由式σ=N·PRF计算得出,在此仿真条件下的通信速率为400 kb/s。
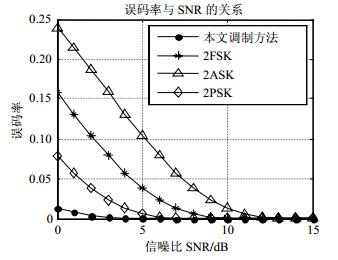
通信性能的另一个指标是传输码元的误码率,图 10仿真了本文调制方法与2FSK、2ASK、2PSK的误码率曲线对比,2FSK、2ASK、2PSK的误码率曲线为理论值,本文调制方式的解调误码率为统计所得,可以看出,本文调制方式的误码率均优于2FSK、2ASK、2PSK,并在误码率达到6 dB时,出现误码率平层。
前面讨论误码率与设计调频率间隔有关,在一定范围内,当设计间隔越大,误码率越低,而在可用带宽内,设计调频率越多,通信速率越高,故能在可接受误码率限定下,在可用带宽内设计更多的调频率来提高通信速率。
4. 结束语
本文设计利用不同调频率的Chirp信号携带通信码元数据实现雷达通信共享,采用主载波进行雷达探测,副载波通过调制调频率实现通信信息传递,并对其雷达性能以及基于分数阶傅里叶变换的解调方法进行了研究,分析了调频率的设计和多普勒影响。可以看出,利用此种方法实现通信对雷达性能基本没有影响,雷达处理系统依然只需要基本处理单元,并没有对雷达的目标检测过程增加额外的负担,而且通信解调还具有抗多普勒能力。可以说,共享信号的设计实现了电子平台中雷达和通信信号能量和时间的共享,这将是未来共享电子战系统的一个重要的发展方向[15]。
-
[1] 上官瑞春. 基于chirp扩频技术的雷达通信一体化研究[D]. 西安: 西安电子科技大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013113505.htm SHANGGUAN Rui-chun. Research on radarcommunication integration system based on chirped spread-spectrum techniques[D]. Xi'an:Xidian University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013113505.htm
[2] TAVIK G C, HILTERBRICK C I, EVINS J B, et al. The advanced multifunction RF concept[J]. IEEE Transaction on Microwave Theory and Techniques, 2005, 53(3):1009-1020. DOI: 10.1109/TMTT.2005.843485
[3] 何献武, 朱洪伟, 唐小明.雷达通用数据链发展概述[J].舰船电子工程, 2010, 30(9):36-38. http://www.cqvip.com/QK/95027A/201009/35367132.html HE Xian-wu, ZHU Hong-wei, TANG Xiao-ming. Introduction to radar common data link[J]. Ship Electronic Engineering, 2010, 30(9):36-38. http://www.cqvip.com/QK/95027A/201009/35367132.html
[4] 刘志鹏. 雷达通信一体化波形研究[D]. 北京: 北京理工大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015801332.htm LIU Zhi-peng. Waveform research on integration of radar and communication[D]. Beijing:Beijing Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015801332.htm
[5] TAKAHARA H, OHNO K, ITAMI M. A study on UWB radar assisted by inter-vehicle communication for safety applications[C]//International Conference on Vehicular Electronics and Safety. Turkey:IEEE, 2012. http://ieeexplore.ieee.org/document/6294272/
[6] MISHRA A K, INGGS M. FOPEN capabilities of commensal radars based on whitespace communication systems[C]//Electronics, Computing and Communication Technologies. Bangalore:IEEE, 2014. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6740313
[7] TAKASE H, SHINRIKI M. A dual use radar and communication system with complete complementary codes[C]//International Radar Symposium. Gdansk:IEEE, 2014. http://ieeexplore.ieee.org/document/6869268/
[8] 陈兴波, 王小谟, 曹晨, 等.雷达通信综合化波形设计技术分析[J].现代雷达, 2015, 35(12):56-63. http://www.cnki.com.cn/Article/CJFDTotal-XDLD201312014.htm CHEN Xing-bo, WANG Xiao-mo, CAO Chen, et al. Techniques analysis of radar-communication integrating waveform[J]. Modern Radar, 2015, 35(12):56-63. http://www.cnki.com.cn/Article/CJFDTotal-XDLD201312014.htm
[9] 李晓柏, 杨瑞娟, 陈新永, 等.基于分数阶傅里叶变换的雷达通信一体化信号共享研究[J].信号处理, 2012, 28(4):487-494. http://www.doc88.com/p-7374384536646.html LI Xiao-bai, YANG Rui-juan, CHEN Xin-yong, et al. The sharing signal for integrated radar and communication based on FRFT[J]. Signal Processing, 2012, 28(4):487-494. http://www.doc88.com/p-7374384536646.html
[10] 孙延坤. 雷达通信一体化波形的机载应用研究[D]. 成都: 电子科技大学, 2013. SUN Yan-kun. The airborne applied research of the waveform of radar-communication integration[D]. Chengdu:University of Electronic Science and Technology of China, 2013.
[11] 杨瑞娟, 陈小民, 李晓柏, 等.雷达通信一体化共享信号技术研究[J].空军预警学院学报, 2013, 27(1):39-43. http://www.cqvip.com/QK/90454A/201301/45799834.html YANG Rui-juan, CHEN Xiao-min, LI Xiao-bai, et al. Research on signal sharing for radar and communication integration[J]. Journal of Air Force Early Warning Academy, 2013, 27(1):39-43. http://www.cqvip.com/QK/90454A/201301/45799834.html
[12] 肇启明, 张钦宇, 张乃通, 等.多进制chirp-rate键控调制及分数傅里叶变换法解调[J].通信学报, 2010, 31(6):1-6. http://mall.cnki.net/magazine/Article/TXXB201006004.htm ZHAO Qi-min, ZHANG Qin-yu, ZHANG Nai-tong, et al. Multiple chirp-rate shift keying and a demodulation method based on fractional Fourier transform[J]. Journal on Communications, 2010, 31(6):1-6. http://mall.cnki.net/magazine/Article/TXXB201006004.htm
[13] 赵兴浩, 邓兵, 陶然.分数阶傅里叶变换数值计算中的量纲归一化[J].北京理工大学学报, 2005, 25(4):360-364. http://www.doc88.com/p-001848217815.html ZHAO Xing-hao, DENG Bing, TAO Ran. Dimensional normalization in the digital computation of the fractional Fourier transform[J]. Transactions of Beijing Institute of Technology, 2005, 25(4):360-364. http://www.doc88.com/p-001848217815.html
[14] 邓兵, 陶然, 平殿发.基于分数阶Fourier变换的chirprate调制解调方法研究[J].电子学报, 2008, 36(6):1078-1083. http://www.wenkuxiazai.com/doc/161e0d6727d3240c8447ef6b.html DENG Bing, TAO Ran, PING Dian-fa. Study on chirp-rate modulation and demodulation based on fractional Fourier transform[J]. Acta Electronica Sinica, 2008, 36(6):1078-1083. http://www.wenkuxiazai.com/doc/161e0d6727d3240c8447ef6b.html
[15] PUJARA C, MEHTA P, DESAI U B. Chirp based multiple access technique using fractional Fourier transform[C]//20076th International Conference on Information, Communications & Signal Processing. Singapore:IEEE, 2007:1301-1305.
-
期刊类型引用(14)
1. 孙文,孙吉利,卢虹良. 基于非匹配滤波的SAR通信一体化技术. 中国科学院大学学报(中英文). 2024(03): 387-397 .  百度学术
百度学术
2. 应士君,杨荣华. 基于PC-BICM的航海雷达通信一体化信号设计及性能分析. 上海海事大学学报. 2024(04): 17-22 .  百度学术
百度学术
3. 李轩,周逸潇,赵尚弘,王国栋,朱子行,李赫,于龙强. 基于线性调频的雷达通信一体化波形研究进展. 激光与光电子学进展. 2023(05): 43-55 .  百度学术
百度学术
4. 李轩,周逸潇,赵尚弘,王国栋. 雷达通信一体化资源复用、波形共享和微波光子研究进展. 信号处理. 2023(12): 2115-2130 .  百度学术
百度学术
5. 李国琳,郭文彬. 雷达通信一体化波形设计综述. 移动通信. 2022(05): 38-44 .  百度学术
百度学术
6. 杨超,张逸格,郑霖. 基于波形共用机制的雷达通信一体化研究进展. 无线电通信技术. 2021(02): 131-140 .  百度学术
百度学术
7. 刘智星,全英汇,肖国尧,邢孟道. 基于PRI捷变的雷达通信一体化共享信号设计方法. 系统工程与电子技术. 2021(10): 2836-2842 .  百度学术
百度学术
8. 隋广洲,于洋. 灾害救援探测机械雷达信号同步传递模型构建. 灾害学. 2020(01): 175-178 .  百度学术
百度学术
9. 韩小振,张锐,蒙林,李海龙,杨文军. 窄脉冲探测通信一体化研究. 信息通信. 2020(11): 43-46 .  百度学术
百度学术
10. 姜孟超,廖桂生,杨志伟,王诏丰. 一种NLFM-CPM雷达通信一体化信号设计. 系统工程与电子技术. 2019(01): 35-42 .  百度学术
百度学术
11. 杜路泉. 基于MATLAB仿真的语音信号分析. 湖南工业职业技术学院学报. 2019(01): 19-24+42 .  百度学术
百度学术
12. 张秋月,张林让,谷亚彬,周宇. 恒包络OFDM雷达通信一体化信号设计. 西安交通大学学报. 2019(06): 77-84 .  百度学术
百度学术
13. 杜路泉. 基于MATLAB仿真的模拟乘法器AM波分析. 装备制造与教育. 2018(03): 51-56 .  百度学术
百度学术
14. 杜路泉. 基于MATLAB仿真的模拟乘法器AM波分析. 绵阳师范学院学报. 2018(11): 30-36+55 .  百度学术
百度学术
其他类型引用(27)

 ISSN
ISSN 


 下载:
下载: