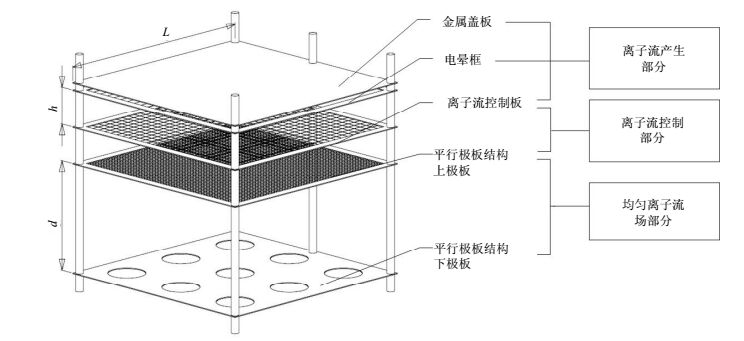
缩小尺寸直流离子流场发生装置如图 1所示，由离子流产生部分、离子流控制部分和均匀直流离子流场3部分组成。离子流产生部分由金属盖板、平行排列的电晕丝和离子流控制网板组成，通过给电晕丝加载直流高压电源使之发生电晕放电的方法产生空间电荷，加载直流高压的金属盖板吸收异极性离子，驱动同极性离子向下运动形成离子流。离子流控制部分由离子流控制板和平行板电场上极板组成，控制加载在离子流控制板和平行板电场上极板间的电场强度能够控制进入平行板电场的离子流的大小。均匀直流离子流场部分由平行极板结构电场组成，其中上极板是金属网板，下极板上布置威尔逊板^[4-5]。离子流经过上极板均匀布置的细密网眼进入平行板电场，形成均匀离子流场。由如图 1所示布置在下极板上的9个威尔逊板(S₁~S₉)监测离子流电流强度，分析离子流场均匀性。在均匀直流离子流场部分进行电场传感器的测试标定。

图  1  直流离子流场发生装置结构

离子流产生部分采用电晕丝电晕放电产生空间电荷，起晕场强计算公式^[6]为：

式中，E_s表示电晕起始场强，单位为kV/cm；E₀和K表示相应参数，由给电晕丝加载的电压特性决定；r表示电晕丝半径；m表示电晕丝表面的粗糙程度，理想情况下电晕丝表面平滑则m=1；δ表示电晕丝周围空气的相对密度，标准情况下为δ=1。实际计算时，E₀一般情况选取31.5，K选取0.305；当电晕丝表面不光滑且全面电晕放电时m=0.82，实际起晕场强计算公式^[7-10]为：。

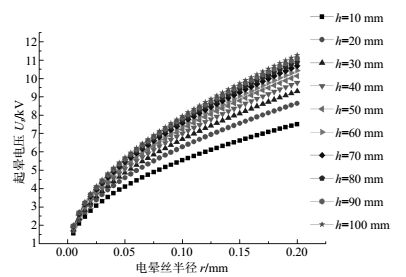
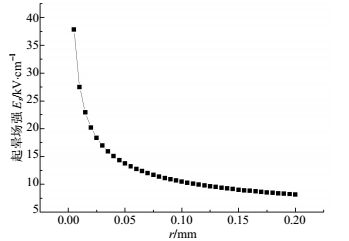
式(3)为起晕电压的计算公式，其中h表示离子流产生区域间距。由式(2)与式(3)可以得到不同离子流产生区域间距h时，电晕丝半径r与起晕电压U_s关系曲线如图 2所示，电晕丝半径r与起晕场强E_s的曲线如图 3所示。

图  2  电晕丝半径r离子流产生区域间距h与起晕电压U_s关系

图  3  电晕丝半径r与起晕场强E_s关系

从图 2和图 3可知，电晕丝的半径越小，起晕电压越小，起晕场强越大，越容易发生电晕放电。因此应该选取半径尽量小的电晕丝，但实际应用过程中还需考虑电晕丝的损耗情况。因此本文装置选用r=0.025 mm的不锈钢丝。

由图 2，当电晕丝选用r=0.025 mm的不锈钢丝，h从10 mm变化到100 mm时，起晕电压U_s从3.06 kV增加到4.12 kV。为便于离子流产生同时为了避免电晕丝与离子流控制板发生击穿放电，取h=60 mm，此时起晕电压理论值为3.886 kV。

本文装置均匀离子流场部分采用正方形平行极板结构^[11]，其关键参数为平行极板边长L和极板间距d，理想电场E计算公式为：

式中，U为平行极板间电压。

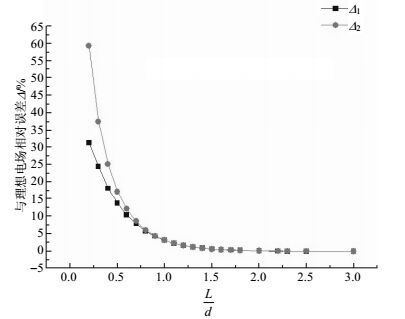
基于有限元理论建立平行极板结构模型，其中E₁和E₂表示两平行极板中间位置和下极板表面中心位置电场强度，加载不同L与d可以获得如图 4所示E₁和E₂分别与E的相对误差随L/d的变化曲线。其中△₁表示E₁与E的相对误差，△₂表示E₂与E的相对误差。

图  4  电场强度相对误差与L/d的关系曲线

由图 4可以得到当平行板尺寸L与平行板间距d满足式(5)关系时，△₁≤0.15%，有：

均匀离子流场部分用于电场传感器的测试标定，在优化平行板结构时候需要考虑电场传感器的放置对电场造成的影响。电场传感器在平行极板结构的下极板中心处进行测试标定时，平行板间距d与传感器测试孔半径R需要满足式(6)关系，此时电场强度相对误差小于0.32%^[2]。在两平行板中间位置对电场传感器进行测试标定时电场强度相对误差为：

式中，v表示放入电场中传感器的体积^[12]。针对边长为50 mm的立方体电场传感器，若在平行极板下极板中心位置进行测试标定时，需要满足d≥200 mm；若在平行极板中间位置进行测试标定时，由式(7)计算可得当d≥232 mm时，电场相对误差△≤1%。

综上本文将均匀离子流场部分平行极板结构尺寸确定为L×L×d=600 mm×600 mm×250 mm，此时L/d=2.4，△₁与△₂均小于0.15%，且对边长小于50 mm的立方体电场传感器在测试标定时所带来的电场强度相对误差小于0.8%。与IEEE有关直流离子流电场测量的标准中的装置相比，本文装置面积仅为其传统装置体积的1/8。

边缘效应是指在实际设计平行极板结构过程中，极板边缘处电场发生畸变导致电场分布不均匀，实际电场与理论电场存在偏差的情况^[13]。受边缘效应影响平行极板结构间均匀电场区域小于理想状况，且电场均匀性误差很大。对于带有空间离子流的电场环境，边缘效应导致的电场不均匀分布会引起空间离子流在平行板电场中的不均匀分布，继而影响均匀离子流场环境的产生。

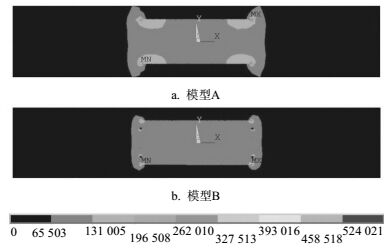
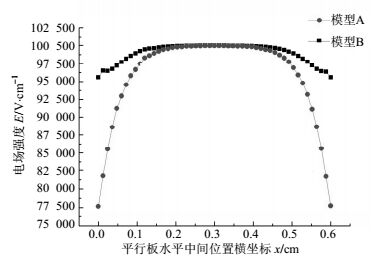
为了解决这一问题，本文采用了在平行板边缘处等分电位的方法进行结构优化，即将平行板四周分成若干层等位线环，每层线环之间用高阻值电阻连接进行分压。利用ANSYS有限元分析软件，分别对结构优化前和优化后的装置进行仿真分析。建立尺寸为L×L×d=600 mm×600 mm×250 mm的模型A和在模型A基础上添加5条等分电位线进行结构优化的模型B，在平行板间加载+2.5 kV直流电压，则两模型的电场分布情况如图 5所示。

图  5  模型A与模型B电场均匀性二维仿真结果

模型A、模型B的电场均匀性仿真结果分别如图 5a、图 5b所示。从图 5中可以很明显看到模型A边缘处的电场不均匀。模型A与模型B电场强度分布曲线如图 6所示。分别选模型A、模型B进行电场均匀性误差分析。模型A电场强度理论值为10 kV/m，平行极板边缘处电场为7.571 kV/m，电场均匀性误差为22.339%，电场均匀性误差小于0.5%的区域为模型A平行板电场中心区域240 mm×240 mm范围内。

图  6  模型A与模型B电场强度分布曲线

模型B电场强度理论值为10 kV/m，平行极板边缘处电场为9.557 kV/m，电场均匀性误差为4.427%。电场均匀性误差小于0.5%的区域为模型B平行板电场中心区域336 mm×336 mm范围内。选模型B平行板电场中心区域240 mm×240 mm范围，计算得到电场均匀性误差为0.147%。从仿真和计算结果可以看出采用平行板边缘等分电位方法能够有效减小电场均匀性误差，增大平行极板间均匀电场区域范围。

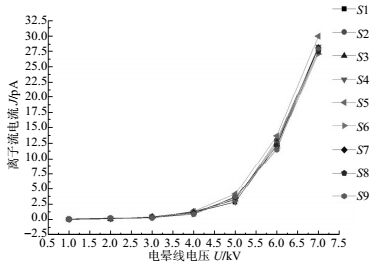
缩小尺寸直流离子流场发生装置实际设计结构如图 7所示，电晕框采用直径0.05 mm的不锈钢丝平行排列组成，其下方60 mm是离子流控制板。离子流控制板下方是边长为600 mm、间距为250 mm的平行极板。如图 1所示在下极板上布置S₁~S₉ 9个圆形威尔逊板，利用吉时利6517B静电计分别测量各位置威尔逊板的离子流电流。在温度为25 ℃，相对湿度为36%，一个标准大气压的环境下对电晕丝加载直流高压进行离子电流分布实验，实验结果如图 8所示。

图  7  直流离子流场发生装置

图  8  S₁~S₉位置离子流电流变化曲线

从图 8中可以看出S₁~S₉各威尔逊板测得的离子流电流分布情况一致，在电晕线电压为4~5 kV左右时离子流电流开始增大，但此时离子流电流很微弱受环境影响很大。因此选取电晕线电压为7 kV时的测量值进行分析。此时9个威尔逊板测得的离子流电流平均值为28.130 pA，测量值的最大偏差仅为1.832 pA，最大相对偏差为6.51%，相对平均偏差仅为1.66%。

本文设计了缩小尺寸的直流离子流场发生装置。基于理论计算对离子流产生部分结构进行了优化设计，确定了电晕丝半径r和离子流场产生区域间距。基于有限元理论对均匀离子流场平行板结构进行了建模仿真，确定了直流离子流场平行板结构的尺寸L和间距d，将装置体积减小为传统装置体积的1/8。采用在平行板边缘处等分电位的方法解决了边缘效应造成的电场不均匀问题，将平行板结构边缘处电场均匀性误差从22.339%降到了4.427%，改善了电场均匀性，增大了平行极板结构中的均匀电场区域范围。最后离子电流分布实验验证了缩小尺寸直流离子流场发生装置的离子流场的均匀性，在电晕丝电压7 kV时离子流电流强度相对平均偏差仅为1.66%，该装置能够提供均匀的离子流场环境。

缩小尺寸直流离子流场发生装置与传统离子流场发生装置相比具有体积小，对高压电源要求低，适用于电场传感器外场环境的现场测试校准，易于集成环境载荷进行传感器环境影响因素研究等优点。本文装置能够为离子流环境下电场的准确测量提供便利和保障，为电场传感器在离子流环境下的输出特性研究提供基础，有利于新型电场传感器的应用和研究发展。