ISSN 
-
在工程中，通常会出现各种各样的不确定性问题，如外部载荷、材料的属性、加工尺寸、近似模型误差等，不确定性是影响结构可靠性最为关键的因素之一[1-2]。不确定性通常可以分为两大类：随机不确定性和认知不确定性[3]。随机不确定性是由于事物的固有波动性引起的，在数学中通常可以用随机变量进行建模。认知不确定性由于数据不足、信息量少等引起的，可用区间理论、模糊数学、可能性理论等进行描述。
机械零部件通常有多种失效模式(如疲劳、磨损、腐蚀等)，由于各失效模式通常有共享变量及相同的因素影响，因而有较强的非线性相关性。多失效模式可靠性方法一直是待解决的难点问题，相关学者相继提出了一系列方法，如二阶窄方法[4]、互补交集模型[5]、鞍点近似法[6]等。然而，大多数现有多失效模式可靠性方法只能刻画线性相关性，而对非线性问题不能有效解决。不仅如此，现有方法大多集中在随机不确定性下，混合不确定性下的多模式可靠性方法研究鲜有报道。近年来，Copula函数被用于对变量及失效模式间复杂非线性相关问题进行建模[7]。文献[8]提出了基于鞍点近似及Copula函数的结构系统可靠性分析方法；文献[9]提出了基于高斯Copula函数的可靠性设计优化方法；文献[10]用Copula函数对相关性进行建模，详细分析了假定失效模式间相互独立在可靠性分析中存在的误差。虽然基于Copula函数多失效模式可靠性分析有了相应的研究，但是绝大部分建立在随机不确定下，混合不确定下基于Copula函数的结构系统可靠性分析方法鲜有报道。针对工程中普遍存在的混合不确定性问题，分别用随机变量和区间变量对随机和认知不确定性进行建模，为了提高计算效率，用先进的仿真方法对随机变量进行采样从而确定性能函数的极值响应。为了最大限度地减少人为主观信息等带来的误差，利用最大熵方法对极值响应进行分布近似，通过Copula函数最终近似确定系统失效概率的最大和最小值。最后给出一个工程算例验证本文方法的精度和有效性。
-
记随机矢量$\boldsymbol{X} = ({X_1}, {X_2}, \cdots, {X_n})$，区间矢量$\boldsymbol{Y} = ({Y_1}, {Y_2}, \cdots, {Y_m})$, ${\boldsymbol{Y}^L} \leqslant \boldsymbol{Y} \leqslant {\boldsymbol{Y}^U}$, ${\boldsymbol{Y}^L}$、${\boldsymbol{Y}^U}$分别表示区间变量取值的上下界。则系统的第$i$个失效模式的性能函数可表示为：
$${Z_i} = {g_i}(\boldsymbol{X}, \boldsymbol{Y})$$ (1) 式中，${Z_i}$为第$i$个性能函数的输出响应，$i = 1, 2, \cdots, K$。
设随机变量${X_i}$的分布函数为${F_{{X_i}}}$，则${X_i}$的${N_r}$个样本可表示为：
$$x_i^j = F_{{X_i}}^{ - 1}(u_i^j)$$ (2) 式中，$F_{{X_i}}^{ - 1}$为${X_i}$分布函数的反函数；$u_i^j$为区间[0, 1]上任意一个样本。由式(2)可知，随机矢量$\boldsymbol{X}$的${N_r}$个样本可表示为${\boldsymbol{x}^j}$，$j = 1, 2, \cdots, {N_r}$。为了提高效率，可用拉丁方进行采样。
基于随机矢量$\boldsymbol{X}$的${N_r}$个样本，则第$i$个性能函数在区间变量上的极值响应(最大和最小值)分别表示为：
$$\begin{gathered} {(Z_i^j)^L} = \min {g_i}({\boldsymbol{x}^j}, \boldsymbol{Y}) \hfill \\ {\rm{s}}{\rm{.t}}{\rm{. }}{\boldsymbol{Y}^L} \leqslant \boldsymbol{Y} \leqslant {\boldsymbol{Y}^U} \hfill \\ \end{gathered} $$ (3) $$\begin{gathered} {(Z_i^j)^U} = \max {g_i}({\boldsymbol{x}^j}, \boldsymbol{Y}) \hfill \\ {\rm{s}}{\rm{.t}}{\rm{. }}{\boldsymbol{Y}^L} \leqslant \boldsymbol{Y} \leqslant {\boldsymbol{Y}^U} \hfill \\ \end{gathered} $$ (4) 现有很多优化方法可用来求解式(3)和式(4)的优化模型，如遗传算法、序列规划算法等。由式(3)和式(4)可得系统${N_r}$个最小和最大值响应分别为：
$${({z^s})^L} = (z_1^L, z_2^L, \cdots, z_K^L)$$ (5) $${({z^s})^U} = (z_1^U, z_2^U, \cdots, z_K^U)$$ (6) 式中，${({z^s})^L}$、${({z^s})^U}$分别表示系统的最小和最大值响应；$z_i^L$、$z_i^U$分别表示第$i$个性能函数${N_r}$个最小和最大值响应。
-
最大熵原理为在现有的数据和样本情况下，确定出熵最大的一种概率分布作为现有数据和样本量的概率分布函数。由于最大熵在近似随机变量的概率密度函数时不需要任何额外的人为主观信息及假设，因此是一种精度较高的方法[11]。利用最大熵原理近似随机变量$Z$的分布可表示为[12]：
$${M_0}(Z) = \max \int_{{S_z}} { - p(z)} \ln p(z){\rm{d}}z$$ (7) 满足以下约束：
$$\int_{{S_z}} {p(z)} {\rm{d}}z = 1$$ (8) $$\int_{{S_z}} {{z^i}} p(z){\rm{d}}x = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} _i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1, 2, \cdots, {k_0}$$ (9) 式中，$p(Z)$为随机变量$Z$的概率密度函数；${S_z}$为积分域；${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} _i}$为第$i$阶原点矩。
根据拉格朗日乘子法，$p(Z)$可表示为：
$$p(Z) = \exp \left( { - {\lambda _0} - \sum\limits_{i = 1}^{{k_0}} {{\lambda _i}{Z^i}} } \right)$$ (10) 式中，${\lambda _i}$为待定的拉格朗日乘子，可用牛顿迭代优化算法求得。
研究表明，在一般运用中仅用前四阶矩即可满足精度要求，由式(5)和式(6)可知，第$k$个失效模式最小和最大值响应的前四阶矩可表示为：
$${(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} _i^k)^L} = \frac{1}{{{N_r}}}\sum\limits_{j = 1}^{{N_r}} {{{\left[{{{(z_k^j)}^L}} \right]}^i}} $$ (11) $${(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} _i^k)^U} = \frac{1}{{{N_r}}}\sum\limits_{j = 1}^{{N_r}} {{{\left[{{{(z_k^j)}^U}} \right]}^i}} $$ (12) 式中，$i = 1, 2, \cdots, 4$。
由式(10)~式(12)，则第$k$个失效模式最小和最大值响应的最大熵密度函数为：
$$p_k^L(Z) = \exp \left( { - \lambda _0^L - \sum\limits_{i = 1}^4 {\lambda _i^L{Z^i}} } \right)$$ (13) $$p_k^U(Z) = \exp \left( { - \lambda _0^U - \sum\limits_{i = 1}^4 {\lambda _i^U{Z^i}} } \right)$$ (14) 式中，$\lambda _i^L$和$\lambda _i^U$分别为对应的拉格朗日乘子。
由式(13)、式(14)可知第$k$个失效模式的失效概率最小和最大值分别可计算为：
$$P_{{f_k}}^{\min } = \int_{ - \infty }^0 {p_k^U(z){\rm{d}}z} = \int_{ - \infty }^0 {\exp \left( { - \lambda _0^U - \sum\limits_{i = 1}^4 {\lambda _i^U{z^i}} } \right)} {\rm{d}}z$$ (15) $$P_{{f_k}}^{\max } = \int_{ - \infty }^0 {p_k^L(z){\rm{d}}z} = \int_{ - \infty }^0 {\exp \left( { - \lambda _0^L - \sum\limits_{i = 1}^4 {\lambda _i^L{z^i}} } \right)} {\rm{d}}z$$ (16) 式(15)、式(16)中的积分没有解析解，可借助辛普森或梯形积分算法求解。
-
设$F({X_1}, {X_2}, \cdots, {X_{{n_s}}})$为具有边缘分布${F_{{X_1}}}({X_1}), $ ${F_{{X_2}}}({X_2}), \cdots, {F_{{X_{{n_s}}}}}({X_{{n_s}}})$的${n_s}$维联合分布函数，由文献[13]可知存在一个Copula函数$C({u_1}, {u_2}, \cdots, {u_{{n_s}}})$，满足：
$$F({X_1}, {X_2}, \cdots, {X_{{n_s}}}) = C\left[{\left. {{F_{{X_1}}}({X_1}), \cdots, {F_{{X_{{n_s}}}}}({X_{{n_s}}})} \right|\theta } \right]$$ (17) 式中，$\theta $为Copula函数的参数。若${F_{{X_1}}}({X_1}), {F_{{X_2}}}({X_2}), \cdots, {F_{{X_{{n_s}}}}}({X_{{n_s}}})$全为连续的边缘分布函数，则Copula函数$C({u_1}, {u_2}, \cdots, {u_{{n_s}}})$唯一确定。为了方便和简单起见，仅考虑二元Copula函数的情况，多元Copula函数情况可在此基础上类推，常见二元Copula函数如下[14]：
Clayton Copula函数：
$$C(\left. {u, v} \right|\theta ) = {({u^{ - \theta }} + {v^{ - \theta }} - 1)^{{1 \mathord{\left/ {\vphantom {1 \theta }} \right. } \theta }}}$$ Gumbel Copula函数：
$$C(\left. {u, v} \right|\theta ) = \exp \left\{ { - {{\left[{{{(-\ln u)}^\theta } + {{(-\ln v)}^\theta }} \right]}^{{1 \mathord{\left/ {\vphantom {1 \theta }} \right. } \theta }}}} \right\}$$ Gauss Copula函数：
$$\begin{gathered} \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{}&{} \end{array}C(\left. {u, v} \right|\theta ) = \hfill \\ \int_{ - \infty }^{{\phi ^{ - 1}}(u)} {\int_{ - \infty }^{{\phi ^{ - 1}}(v)} {\frac{1}{{2{\rm{ \mathsf{ π} }}\sqrt {1 - {\theta ^2}} }}} } \exp \left[{\frac{{2\theta s\omega-{s^2}-{\omega ^2}}}{{2(1-{\theta ^2})}}} \right]{\rm{d}}s{\rm{d}}\omega \hfill \\ \end{gathered} $$ -
由式(17)可知，具有两个失效模式串联系统的失效概率可表示为：
$$\begin{gathered} {P_{{f_s}}} = P\left[{{g_1}(\boldsymbol{X}, \boldsymbol{Y}) < 0 \cup {g_2}(\boldsymbol{X}, \boldsymbol{Y}) < 0} \right] = \\ {P_{{f_1}}} + {P_{{f_2}}} - C(\left. {{P_{{f_1}}}, {P_{{f_2}}}} \right|\theta ) \\ \end{gathered} $$ (18) 式中，${P_{{f_1}}}, {P_{{f_2}}}$分别为两个失效模式的失效概率。
需指出的是，当系统存在区间变量时候，系统失效概率是区间而非精确值，此时系统失效概率的最大和最小值可分别近似表示为下述优化模型：
$$\begin{gathered} P_{{f_s}}^{\min } = \min \left[{{P_{{f_1}}} + {P_{{f_2}}}-C(\left. {{P_{{f_1}}}, {P_{{f_2}}}} \right|\theta )} \right] \hfill \\ {\rm{s}}{\rm{.t}}{\rm{. }}P_{{f_k}}^{\min } \leqslant {P_{{f_k}}} \leqslant P_{{f_k}}^{\max };j = 1, 2; \hfill \\ \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}{\theta ^L} \leqslant \theta \leqslant {\theta ^U} \hfill \\ \end{gathered} $$ (19) $$\begin{gathered} P_{{f_s}}^{\max } = \max \left[{{P_{{f_1}}} + {P_{{f_2}}}-C(\left. {{P_{{f_1}}}, {P_{{f_2}}}} \right|\theta )} \right] \hfill \\ {\rm{s}}{\rm{.t}}{\rm{. }}P_{{f_k}}^{\min } \leqslant {P_{{f_k}}} \leqslant P_{{f_k}}^{\max };k = 1, 2 \hfill \\ \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}{\theta ^L} \leqslant \theta \leqslant {\theta ^U} \hfill \\ \end{gathered} $$ (20) 式中，${\theta ^U}$和${\theta ^L}$分别为Copula函数参数的上下界，$P_{{f_k}}^{\min }, P_{{f_k}}^{\max }(k = 1, 2)$为第$k$个失效模式的失效概率最小和最大值。
为了确定Copula函数参数的上下界，假定Copula函数的结构不变，首先在区间矢量$\boldsymbol{Y}$的取值范围内随机产生${N_p}$个样本${\boldsymbol{y}^i};i = 1, 2, \cdots, {N_p}$，由最大熵方法可得出两个失效模式分别在$\boldsymbol{Y} = {\boldsymbol{y}^i}$下的最大熵密度函数、分布函数和失效概率${({P_{{f_1}}})_{\boldsymbol{Y} = {\boldsymbol{y}^i}}}$、${({P_{{f_2}}})_{\boldsymbol{Y} = {\boldsymbol{y}^i}}}$。对所得的最大熵分布函数进行采样，并根据分步估计和最大似然估计法，可估计出$\boldsymbol{Y} = {\boldsymbol{y}^i}$下的Copula函数参数${({\hat \theta ^i})_{\boldsymbol{Y} = {\boldsymbol{y}^i}}}$。样本的对数似然函数可表示为：
$$\begin{gathered} \ln L{(\theta )_{\boldsymbol{Y} = {\boldsymbol{y}^i}}} = \sum\limits_{j = 1}^{{N_h}} {\ln c\left[{{F_1}{{(z_1^j)}_{\boldsymbol{Y} = {\boldsymbol{y}^i}}}, {F_2}{{(z_2^j)}_{\boldsymbol{Y} = {\boldsymbol{y}^i}}};\theta } \right]} + \\ \sum\limits_{j = 1}^{{N_h}} {\ln } {p_1}{(z_1^j)_{\boldsymbol{Y} = {\boldsymbol{y}^i}}} + \sum\limits_{j = 1}^{{N_h}} {\ln } {p_2}{(z_2^j)_{\boldsymbol{Y} = {\boldsymbol{y}^i}}} \\ \end{gathered} $$ (21) 式中，${F_1}$和${F_2}$分别表示失效模式1、2的最大熵分布函数；${p_1}$和${p_2}$为在$\boldsymbol{Y} = {\boldsymbol{y}^i}$下的最大熵概率密度函数；${N_h}$为获取的样本量。
在满足一定精度要求的条件下，${\theta ^U}$和${\theta ^L}$可分别近似表示为：
$${\theta ^U} = \max \left[{{{({{\hat \theta }^i})}_{Y = {y^i}}}, i = 1, 2, \cdots, {N_p}} \right]$$ (22) $${\theta ^L} = \min \left[{{{({{\hat \theta }^i})}_{Y = {y^i}}}, i = 1, 2, \cdots, {N_p}} \right]$$ (23) -
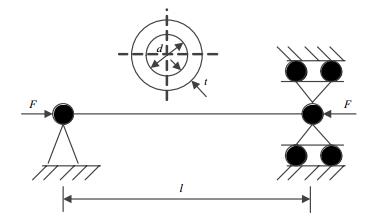
某空心压杆，如图 1所示，具有稳定性及强度两种失效模式，其性能函数分别为：
图 1 空心杆
$${g_1} = \frac{{{{\rm{ \mathsf{ π} }}^2}E\left[{{{(d + 2t)}^4}-{d^4}} \right]}}{{64{l^2}{\rm{d}}t}} - \frac{F}{{{\rm{ \mathsf{ π} d}}t}}$$ $${g_2} = S - \frac{F}{{{\rm{ \mathsf{ π} d}}t}}$$ 式中，$F$、$E$、$S$、$d$、$t$、$l$分别表示轴向载荷、材料弹性模量、材料屈服极限、截面中径、壁厚和杆长，单位分别为kN、GPa、MPa、mm、mm、mm。为了说明本文方法的有效性，壁厚假定为区间变量，其上下界分别为2.42 mm和2.38 mm。变量的相关分布信息如表 1所示。
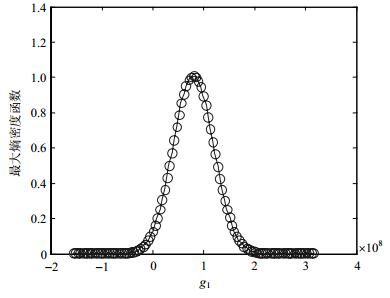
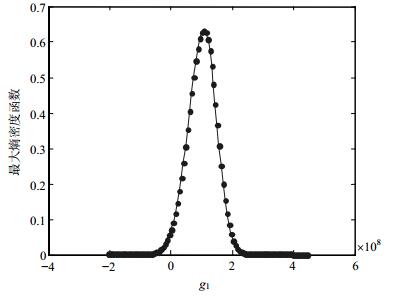
表 1 变量的分布信息
变量 均值 方差 分布类型 F 120.0 12.000 0 正态 E 203.0 4.000 0 正态 S 490.0 40.000 0 正态 d 42.5 0.212 5 正态 l 1 090.0 5.450 0 正态 为了求解各失效模式失效概率的最大和最小值，首先用拉丁方采样方法对各随机变量进行采样，样本量为5 000。由式(3)、式(4)可得样本在区间变量上的最大和最小值，并分别进行最大熵密度函数估计，如${g_1}$、${g_2}$响应最大值的最大熵密度函数分别如图 2和图 3所示。由式(15)、式(16)可得失效模式${g_1}$、${g_2}$失效概率的最大和最小值。需特别指出的是，变量$t$为区间变量，只代表其可在区间范围内任意取值，而并不知道其任何其他信息，因此不能等同于其在所取值范围内均匀分布。另外，选择Copula函数对失效模式相关性进行建模，由式(22)、式(23)可得参数$\theta $的最大和最小值估计分别为1.92、1.55。
图 2 ${g_1}$响应最大值的密度函数
图 3 ${g_2}$响应最大值的密度函数
为了说明本文方法的精度和有效性，采用蒙特卡罗方法进行对比验证，样本量为${10^6}$。当系统中存在区间变量时，为了确定系统失效概率最大和最小值，可把区间变量平均分成若干小区间，分别计算区间变量在小区间端点时系统的失效概率并确定失效概率的极值，所得系统失效概率最大和最小值如表 2所示。从表 2可知，用本文方法所得的结果与蒙特卡罗所得的结果较为接近。然而，蒙特卡罗方法一般情况下需要大量的样本，因此计算效率低，特别是在混合不确定性下，对于区间变量任意取值，都需要大量的样本进行仿真，因此计算效率极低，在工程中难以适用。
表 2 本文方法与蒙特卡罗仿真所得的结果
方法 失效概率上下界 失效模式${g_1}$ 失效模式${g_2}$ 系统失效概率 蒙特卡罗 $P_f^{\min }$ 0.020 6 0.014 8 0.030 9 $P_f^{\max }$ 0.034 3 0.020 8 0.047 0 本文方法 $P_f^{\min }$ 0.020 4 0.014 3 0.031 8 $P_f^{\max }$ 0.034 0 0.020 2 0.050 9 -
本文对混合不确定性下基于Copula函数及最大熵方法的结构可靠性分析方法进行初步探索性研究，并用算例验证了方法的合理性。
1) 不确定性广泛存在工程中，考虑混合不确定性下的多失效模式可靠性方法更加符合工程实际。
2) Copula函数能有效刻画多失效模式间较强的非线性相关性，可有效构建失效模式间的联合分布函数。当系统中存在区间变量时，Copula函数中的参数估计值为区间而非精确值。
3) 利用最大熵近似极值响应的分布，可有效避免人为主观假设所带来的误差，根据响应的极值可计算失效概率的最大和最小值。
4) 混合不确定性下系统的失效概率为区间而非精确值，计算量较大。一般情况下，采样的样本量越大，所得计算结果更精确。但是，当失效概率较小时，本文方法会带来较大误差。
Structural Reliability Analysis under Mixed Uncertainties
-
摘要: 在工程实际中，部件或者系统的失效是由多失效模式引起的。针对变量和失效模式间复杂非线性相关问题，采用Copula函数进行建模。为了最大限度避免人为主观信息等带来的误差，利用最大熵方法分别近似极值响应的概率密度函数，在此基础上确定各自失效模式失效概率的最大和最小值。采用仿真和最大似然估计法相结合确定Copula函数中参数的最大和最小值。为了近似求解系统失效概率的最大和最小值，给出了相应的优化模型。算例分析表明该模型为混合不确定性及多失效模式相关下的结构可靠性分析提供新途径。Abstract: Components or systems fails are usually caused by multiple failure models in practical engineering. Copula functions are used to model complicated nonlinear corrections between variables and failure modes. To avoid error from subjective hypothesis at utmost, maximum entropy approach is employed for approximating probability density functions of extreme value responses, and the lower and upper bounds of probability of failure can be determined according to the approximated probability density functions. Finally, both simulation and maximum likelihood estimation approaches are used for determining the lower and upper bounds of parameters in selected Copula functions. An optimization model is presented to calculate the lower and upper bounds of system probability of failure. Numerical example has demonstrated that the proposed method is available for structural systems with multiple failure modes under mixed uncertainties.
-
表 1 变量的分布信息
变量 均值 方差 分布类型 F 120.0 12.000 0 正态 E 203.0 4.000 0 正态 S 490.0 40.000 0 正态 d 42.5 0.212 5 正态 l 1 090.0 5.450 0 正态 
下载: 导出CSV
表 2 本文方法与蒙特卡罗仿真所得的结果
方法 失效概率上下界 失效模式${g_1}$ 失效模式${g_2}$ 系统失效概率 蒙特卡罗 $P_f^{\min }$ 0.020 6 0.014 8 0.030 9 $P_f^{\max }$ 0.034 3 0.020 8 0.047 0 本文方法 $P_f^{\min }$ 0.020 4 0.014 3 0.031 8 $P_f^{\max }$ 0.034 0 0.020 2 0.050 9
下载: 导出CSV
-
[1] OKASHA N M. An improved weighted average simulation approach for solving reliability-based analysis and design optimization problems[J]. Structural Safety, 2016, 60:47-55. doi: 10.1016/j.strusafe.2016.01.005 [2] MELCHERS R E. Structural reliability analysis and prediction[M]. 2nd ed. New York:Wiley, 1999. [3] HU Z, MAHADEVAN S, DU Xiao-ping. Uncertainty quantification of time-dependent reliability analysis in the presence of parametric uncertainty[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part B:Mechanical Engineering, 2015, 1(2):04015004. doi: 10.1061/AJRUA6.0000818 [4] DITEVSEN O. Narrow reliability method bounds for structural systems[J]. Journal of Structural Mechanics, ASCE, 1979, 7(4):453-472. doi: 10.1080/03601217908905329 [5] YOUN B D, WANG Ping-feng. A generalized complementary intersection method for system reliability analysis[J]. Journal of Mechanical Design, Transaction of the ASME, 2011, 133(7):74-82. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ0223044802 [6] DU Xiao-ping. System reliability analysis with saddlepoint approximation[J]. Structural and Multidisciplinary Optimization, 2010, 42:193-208. doi: 10.1007/s00158-009-0478-x [7] TANG Xiao-song, ZHOU Chuang-bing, LI D Q, et al. Impact of copulas for modeling bivariate distributions on system reliability[J]. Structural Safety, 2013, 44:80-90. doi: 10.1016/j.strusafe.2013.06.004 [8] 韩文钦, 周金宇.基于鞍点逼近的机械零件可靠性Copula分析方法[J].机械强度, 2013, 35(5):612-616. http://www.cqvip.com/QK/90871X/201305/47412684.html HAN Wen-qin, ZHOU Jin-yu. Copula analysis method of machine components reliability based on saddlepoint approximation[J]. Journal of Mechanical Strength, 2013, 35(5):612-616. http://www.cqvip.com/QK/90871X/201305/47412684.html [9] NOH Y J, CHOI K K, DU L. Reliability-based design optimization of problems with correlated input variables using a Gaussian copula[J]. Structural and Multidisciplinary Optimization, 2009, 38:1-16. doi: 10.1007/s00158-008-0277-9 [10] PARK C Y, KIM N H, HAFTKA RP. The effect of ignoring dependence between failure modes on evaluating system reliability[J]. Structural and Multidisciplinary Optimization, 2015, 52:251-268. doi: 10.1007/s00158-015-1239-7 [11] 童玲, 陈光(衣禹).测量数据处理中的Bayes理论与最大熵方法[J].电子科技大学学报, 2007, 36(1):77-78, 85. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract1791.shtml TONG Ling, CHENG Guang-ju. Bayes theorem and maximum entropy principle in the measurement data processing[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(1):77-78, 85. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract1791.shtml [12] WU Xi-ming. Calculation of maximum entropy densities with application to income distribution[J]. Journal of Econometrics, 2003, 115(2):347-354. doi: 10.1016/S0304-4076(03)00114-3 [13] XI Zhi-min, JING R, WANG Ping-feng, et al. A copula-based sampling method for data-driven prognostics[J]. Reliability Engineering and System Safety, 2014, 132(4):72-82. http://www.sciencedirect.com/science/article/pii/S0951832014001446 [14] 韦艳华, 张世英. Copula理论及其在金融分析上的应用[M].北京:清华大学出版社, 2008. WEI Yan-hua, ZHANG Shi-ying. Copula theory and its application in finance[M]. Beijing:Tsinghua University Press, 2008. -
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 6710
- HTML全文浏览量: 2042
- PDF下载量: 68
- 被引次数: 0
