ISSN 
-
合成孔径雷达(synthetic aperture radar, SAR)作为一种具有全天时、全天候、信息量丰富的遥感成像技术，已成为当今对地观测的重要手段，在地形图像生成、目标探测与侦察、目标精确打击、国土资源勘查和自然灾害监测等国民经济与军事领域得到越来越广泛的应用。因具备三维成像能力，线阵SAR(linear array SAR, LASAR)是近几年来被广泛关注的一种新型SAR成像技术[1-6]。本质上，LASAR成像技术是通过控制线阵天线运动形成虚拟二维面阵获得观测目标二维分辨，并结合脉冲压缩技术得到观测目标的第三维分辨。LASAR可工作于多种成像模式，如下视和前视等，突破了传统SAR成像模式限制与不足(传统SAR通常只能工作于侧视成像模式)。因此，LASAR可灵活方便地实现复杂场景(城市、山区等)及特殊目标(建筑、舰船、坦克等)的高精度三维成像，在全天候、全天时三维地形测绘、目标定位与识别和情报获取等国防军事和资源管理领域有着极大的研究价值和应用前景。
目前，LASAR数据三维成像处理主要采用后向投影(back projection, BP)算法。BP算法基本思路是利用合成阵列天线中每一个天线相位中心(antenna phase center, APC)的位置信息，计算其到投影成像空间中各散射点的距离历史，利用该距离历史实现LASAR回波数据的相干积累成像。由于采用逐APC和逐个投影空间分辨单元相干积累，相对其他频域成像算法，BP算法可在复杂运动轨迹下实现观测场景的高精度成像[7]。但是，BP算法高精度成像时对APC轨迹位置精度要求很高，如在X波段雷达时位置精度通常需要达到毫米级。在LASAR三维观测成像中，一个脉冲重复时间阵列天线中需要成百上千个APC同时工作。因此，仅利用雷达系统中单个位置的导航测量系统(如惯性测量系统或全球定位系统)数据难以实现LASAR多个APC运动误差的精确补偿。为了提高LASAR三维成像质量，在利用导航测量数据进行运动误差补偿后，还需结合回波数据和自聚焦成像技术实现多APC的残余运动误差补偿。
至今，针对传统SAR运动误差补偿问题，学者们已经提出多种基于不同准则的自聚焦成像算法，如最大似然估计(maximum likelihood estimation, MLE)自聚焦、最小熵估计(minimum entropy estimation, MEE)自聚焦、最大锐度(maximum sharpness estimation, MSE)自聚焦等方法。相位梯度自聚焦(phase gradient autofocusing, PGA)算法是一种在SAR实际成像中广泛应用的典型MLE自聚焦成像算法[8]。但是，PGA成像算法前提是观测目标场景包含强散射点目标，并且要求相邻天线相位中心的相位误差变化较平缓，难以适用于陡变和随机相位误差估计。MEE自聚焦方法利用SAR聚焦图像的最小熵准则估计APC的相位误差。然而，SAR图像最小熵有时并没有实现多点观测目标的精确聚焦和恢复。与PGA算法和MEE算法不同，MSE方法主要利用SAR图像的最大锐度作为准则估计APC的相位误差，其通常能实现多点观测目标的精确聚焦和恢复[9]。如文献[10]针对聚束式SAR成像模式，提出了一种基于图像最大锐度的SAR后向投影自聚焦算法。但是，该后向投影自聚焦算法需要利用整个场景分辨单元构造代价估计函数，在大场景成像时该代价估计函数维数过大，难以应用。文献[11]提出了一种基于半正定松弛及圆锥优化的SAR自聚焦成像算法，实测数据结果显示该方法在陡变相位误差条件下性能优于PGA算法和MEE自聚焦方法。但是，该方法同文献[10]中后向投影自聚焦算法一样，在大场景成像时需要构建一个较大维数的代价函数，在LASAR三维成像时计算量大且难以适用。另外，针对LASAR系统中运动误差补偿，近年来也出现了一些基于压缩感知理论的稀疏自聚焦成像方法[12-15]，但是这类方法通常需要观测目标场景具备稀疏特性，在不稀疏时聚焦性能严重下降。
为了补偿LASAR合成阵列天线APC的运动误差，提高LASAR三维成像质量，本文提出了一种基于最大锐度半正定规划的LASAR后向投影自聚焦成像算法。该方法结合LASAR三维图像锐度最大化原则，建立LASAR成像处理半正定规划模型，利用迭代逼近最优方法实现LASAR阵列多APC相位误差进行估计及自聚焦成像。另外，为了提高算法运算效率，本文仅采用主散射目标区域进行APC相位误差估计。仿真数据和实测数据验证了本文算法的有效性。
-
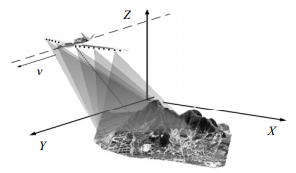
LASAR三维成像典型几何模型如图 1所示，假设系统工作于正下视模式，在观测成像过程中，线阵天线通过机载平台运动合成一个虚拟二维阵列APC。若采用${\mathit{\boldsymbol{P}}_A}$表示这些APC的位置集，则：
图 1 LASAR成像几何模型
$${\mathit{\boldsymbol{P}}_A} = \{ {\mathit{\boldsymbol{p}}_n} = [{x_n},{y_n},{z_n}];n \in \mathit{\Upsilon} \} $$ (1) 式中，集合$\mathit{\Upsilon} = [1,2, \cdots ,N]$表示APC序号，$N$表示LASAR二维APC的总个数。
在高频条件下，可假设观测场景近似为点散射目标组成，并对观测场景进行三维离散化。若观测场景中的点目标位置${\mathit{\boldsymbol{P}}_m}$，其散射系数为${\mathit{\boldsymbol{\sigma }}_s}$，则有：
$${\mathit{\boldsymbol{P}}_m} = \{ {\mathit{\boldsymbol{q}}_m} = [{x_m},{y_m},{z_m}];m \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\} $$ (2) 式中，$\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = [1,2, \cdots ,{M_0}]$表示三维观测离散场景中目标序号集合，${M_0}$表示观测场景分辨单元的总个数。
假设LASAR发射线性调频信号，LASAR原始回波数据经过距离压缩后，观测场景中第$m$个散射点的回波信号可以表示为：
$${s_r}(r,n,m) = {\sigma _m}{\chi _R}(r - {R_{n,m}})\exp ( - {\rm{j}}2{\rm{\mathsf{π} }} k{R_{n,m}})$$ (3) 式中，$r$为LASAR回波数据距离域；$k$为系统波数；${R_{n,m}}$表示场景中散射点${\mathit{\boldsymbol{q}}_m}$到第$n$个天线相位中心${\mathit{\boldsymbol{p}}_n}$的距离；${\chi _R}( \cdot )$表示LASAR距离模糊函数。式(3)中第一项${\chi _R}(r - {R_{n,m}})$对应于目标的距离向分辨力，第二项$\exp ( - {\rm{j}}2{\rm{\mathsf{π} }} k{R_{n,m}})$包含了目标方位向和切航向分辨力。若阵列APC存在运动误差，则会导致${R_{n,m}}$不精确，从而会引入相位误差。当场景包含多个散射点时，整个观测场景的回波信号可以表示为：
$${s_r}(r,n) = \sum\limits_{m \in \mathit{\Omega} } {{s_r}(r,n,m)} $$ (4) -
BP算法基本思路是对观测场景中目标的回波信号进行相干积累。给定后向投影成像空间中的一个散射点${\mathit{\boldsymbol{q}}'_m} = [{x_m},{y_m},{z_m}]$，其到LASAR阵列中第$n$个APC位置的距离可以表示为：
$${R'_{n,m}} = {\left\| {{{\mathit{\boldsymbol{q}}'}_m} - {\mathit{\boldsymbol{p}}_n}} \right\|_2} \;\; m = 1,2, \cdots ,M, \;\; n = 1,2, \cdots ,N$$ (5) 式中，$M$表示投影成像空间中分辨单元的总数。根据BP算法相干积累原理，投影空间中分辨单元${\mathit{\boldsymbol{q}}'_m}$的聚焦信号可以表示为：
$${S_m} = \sum\limits_n {{s_r}({r_m},n){{\rm{e}}^{{\rm{j}}4{\rm{\mathsf{π} }} {R_{n,m}}/\lambda }}} $$ (6) 式中，${s_r}({r_m},n)$表示LASAR距离压缩后的回波数据；${r_m}$为分辨单元${\mathit{\boldsymbol{q}}'_m}$所对应的距离历史单元；$\lambda $为雷达工作波长。为了抑制数据中噪声影响，通常对脉压回波数据进行sinc函数插值获取${s_r}({r_m},n)$。
令${b_{m,n}} = {s_r}({r_m},n){{\rm{e}}^{{\rm{j}}4{\rm{\mathsf{π} }} {R_{n,m}}/\lambda }}$表示BP成像算法中分辨单元${\mathit{\boldsymbol{q}}'_m}$在第$n$个LASAR合成阵列APC回波数据的相干积累回波分量，向量${\mathit{\boldsymbol{b}}_{m,n}} = {[{b_{m,1}},{b_{m,2}}, \cdots ,{b_{m,N}}]^{\rm{T}}}$表示投影成像空间中分辨单元${\mathit{\boldsymbol{q}}'_m}$在所有合成阵列APC所对应的相干积累回波向量。显然，式(6)中BP相干积累聚焦信号可表示为两个向量的乘积形式：
$${S_m} = \mathit{\boldsymbol{b}}_m^{\rm{{\rm T}}}{\mathit{\boldsymbol{I}}_N}$$ (7) 式中，${\mathit{\boldsymbol{I}}_N}$是元素全部是1的维向量。
若LASAR系统不存在运动误差，式(7)中BP算法聚焦过程可进一步表示为如下线性数学模型：
$$\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{I}}_N}$$ (8) 式中，$\mathit{\boldsymbol{B}} = {[{\mathit{\boldsymbol{b}}_1},{\mathit{\boldsymbol{b}}_2}, \cdots ,{\mathit{\boldsymbol{b}}_M}]^{\rm{T}}}$为BP算法的相干积累矩阵；$\mathit{\boldsymbol{S}} = {[{S_1},{S_2}, \cdots ,{S_M}]^{\rm{T}}}$为BP算法的聚焦向量。由式(8)可知，BP算法处理过程可表示为相干积累矩阵$\mathit{\boldsymbol{B}}$与常数向量${\mathit{\boldsymbol{I}}_N}$的乘积。
-
当LASAR系统存在运动误差时，式(3)会存在运动误差引入的相位误差，此相位误差可表示为：
$$\mathit{\boldsymbol{\varphi}} = {[{\varphi _1},{\varphi _2}, \cdots ,{\varphi _N}]^{\rm{T}}}$$ (9) 将式(9)向量$\mathit{\boldsymbol{\varphi }}$代入式(8)中，则BP算法聚焦可以表示为相干积累矩阵$\mathit{\boldsymbol{B}}$与相位误差向量${{\rm{e}}^{j\mathit{\boldsymbol{\varphi }}}}$的相乘：
$$\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{B}}{{\rm{e}}^{{\rm{j}}\mathit{\boldsymbol{\varphi }}}}$$ (10) 若令$\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} $表示相位误差向量$\mathit{\boldsymbol{\varphi }}$的估计值，则相位误差补偿后，BP算法聚焦的信号可表示为：
$$\mathit{\boldsymbol{S}}(\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} ) = \mathit{\boldsymbol{B}}{{\rm{e}}^{{\rm{j}}(\mathit{\boldsymbol{\varphi }} - \mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} )}}$$ (11) 显然，当$\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} = \mathit{\boldsymbol{\varphi }} $时，式(11)等效于式(8)，观测场景可实现高精度聚焦成像。
自聚焦成像算法的目标是利用其图像最优准则对APC相位误差$\mathit{\boldsymbol{\varphi }}$进行估计。结合LASAR图像锐度最大准则，本文可采用以下锐度最优化问题估计LASAR阵列多APC的相位误差：
$${{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown}} _{{\rm{opt}}}} = \arg \; \mathop {\max }\limits_{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} } ||S(\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} )||_2^2$$ (12) -
基于LASAR三维图像锐度最大准则，结合式(11)和式(12)，本文通过解决以下最优化问题实现LASAR合成阵列APC的相位误差估计：
$$\begin{array}{c} {{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }_{{\rm{opt}}}} = \arg \mathop {\max }\limits_{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} } {\mathit{\boldsymbol{S}}^{\rm{H}}}(\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} )\mathit{\boldsymbol{S}}(\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} ) = \\ \arg \mathop {\max }\limits_{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} } {({{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }})^H}\mathit{\boldsymbol{B}}_e^H{\mathit{\boldsymbol{B}}_e}{{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }} \\ \end{array} $$ (13) 式(13)最优化可采用恒定常数二次规划(constant modulus quadratic program, CMQP)方法求解：
$${\mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}} = \arg \mathop {\min }\limits_\gamma {\mathit{\boldsymbol{\gamma }}^{\rm{H}}}\mathit{\boldsymbol{Q}}\mathit{\boldsymbol{\gamma }} {\rm{s}}{\rm{.t }}|{\mathit{\boldsymbol{\gamma }}_n}| = 1, \; n = 1,2, \cdots ,N$$ (14) 式中，$\mathit{\boldsymbol{\gamma }} = {{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }}$为LASAR阵列APC的相位误差向量；$\mathit{\boldsymbol{Q}} = - \mathit{\boldsymbol{B}}_e^{\rm{H}}{\mathit{\boldsymbol{B}}_e}$表示代价目标矩阵。向量$\mathit{\boldsymbol{\gamma }}$最优化估计可等效为在$\mathit{\boldsymbol{\gamma }}$幅度值为1约束条件下的线性最小化求解问题。但是，由于式(14)是非确定性多项式困难问题，当$\mathit{\boldsymbol{\gamma }}$维数大时CMQP等式最优化求解非常困难。因此，一般采用近似估计算法求解CMQP最优解。
近年来，半正定规划方法成为了解决CMQP等式最优化问题的热门方法。相比CMQP问题中的传统特征值分解方法，半正定规划算法估计精度更高。对于CMQP问题求解，半正定规划的典型表达式为：
$$\begin{array}{c} \mathit{\boldsymbol{\hat X}} = \arg \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{X}}} {\rm{tr}}(\mathit{\boldsymbol{QX}}) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\mathit{\boldsymbol{X}} \geqslant 0,{\rm{tr}}({\mathit{\boldsymbol{C}}_n}\mathit{\boldsymbol{X}}) = {g_n} \;\; n = 1,2, \cdots ,N \\ \end{array} $$ (15) 式中，$\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{\gamma }}{\mathit{\boldsymbol{\gamma }}^{\rm{H}}}$表示相位误差矩阵；${\rm{tr}}( \cdot )$表示矩阵对角元素之和。因${\mathit{\boldsymbol{\gamma }}^{\rm{H}}}\mathit{\boldsymbol{Q}}\mathit{\boldsymbol{\gamma }} = {\rm{tr}}(\mathit{\boldsymbol{\gamma }}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{\gamma }}^{\rm{H}}}) = {\rm{tr}}(\mathit{\boldsymbol{Q}}\mathit{\boldsymbol{\gamma }}{\mathit{\boldsymbol{\gamma }}^{\rm{H}}})$，式(15)中CMQP等式最优化求解可近似转换为以下半正定矩阵的最优化估计问题：
$$\begin{array}{c} {{\mathit{\boldsymbol{\hat X}}}_{{\rm{opt}}}} = \arg \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{X}}} {\rm{tr}}(\mathit{\boldsymbol{QX}}) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\mathit{\boldsymbol{X}} \geqslant 0,{\mathit{\boldsymbol{X}}_{ii}} = {g_n} \;\; n = 1,2, \cdots ,N \\ \end{array} $$ (16) 为了求解式(16)中的半正定规划问题，可利用现有的一些经典凸优化算法进行估计，如共轭梯度方法、内点法等。另外，目前许多学者也开发了各种半正定规划求解软件工具箱，如CVX工具箱、SDPSOL软件等，可用于式(16)快速有效求解。值得注意的是，式(16)中的目标矩阵$\mathit{\boldsymbol{Q}}$与文献[8]的目标矩阵不同。获得矩阵${\mathit{\boldsymbol{\hat X}}_{{\rm{opt}}}}$后，最优向量${\mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}}$可以通过矩阵${\mathit{\boldsymbol{\hat X}}_{{\rm{opt}}}}$分解得到，具体实现可采用文献[8]的方法。若${\mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}}$已估，则LASAR阵列APC的相位误差向量可以表示为：
$$\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} = - \angle {\mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}}$$ (17) -
为了提高相位误差$\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} $的估计精度并且减少估计过程的运算量，本文半正定规划自聚焦算法中仅采用主散射区域构造式(14)中代价目标矩阵。与PGA算法和最小熵算法相似，主散射点区域的估计采用以下方法：1)在距离压缩后回波数据中根据图像强度选择主散射目标距离单元；2)根据所选主散射目标距离单元图像估计目标主瓣宽度；3)根据目标主瓣宽度通过阈值选择主散射目标区域。
获取主散射目标区域后，令$\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = [1,2, \cdots ,{M_0}]$表示主散射目标的序列集合，${M_0}$是主散射目标单元的总个数。此时，式(8)中主散射目标区域$\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}$对应的后向投影算法的相干积累矩阵变为${\mathit{\boldsymbol{B}}_\mathit{\Omega} } = {[{\mathit{\boldsymbol{b}}_1},{\mathit{\boldsymbol{b}}_2}, \cdots ,{\mathit{\boldsymbol{b}}_{{M_0}}}]^{\rm{T}}} \subset \mathit{\boldsymbol{B}}$。
本文基于最大锐度半正定规划的LASAR后向投影自聚焦算法如算法1所示，其主要步骤是迭代最优估计过程。
算法1：最大锐度半正定规划后向投影自聚焦
输入：矩阵${\mathit{\boldsymbol{B}}_\mathit{\Omega} }$，门限$\delta $，迭代次数$K$。
输出：散射稀疏向量$\mathit{\boldsymbol{S}}$，相位误差向量${{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown}} _{{\rm{opt}}}}$。
初始化：$\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} = 0$，$k = 0$，${\mathit{\boldsymbol{B}}^{(0)}} = \mathit{\boldsymbol{B}}{\rm{diag}}\{ {{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }}^{(0)}\} $。
while $||{\mathit{\boldsymbol{S}}^{(k + 1)}} - {\mathit{\boldsymbol{S}}^{(k)}}||/||{\mathit{\boldsymbol{S}}^{(k)}}|| > \delta $ and $k \leqslant K$ do
1) 构造目标矩阵：
${\mathit{\boldsymbol{B}}^{(k + 1)}} = {\mathit{\boldsymbol{B}}^{(k)}}{\rm{diag}}\{ {{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }}^{(k)}\} $，${\mathit{\boldsymbol{Q}}^{(k + 1)}} = - {(\mathit{\boldsymbol{B}}_e^{(k + 1)})^{\rm{H}}}\mathit{\boldsymbol{B}}_e^{(k + 1)}$
2) 最大锐度半正定规划估计：
$$\begin{array}{c} \mathit{\boldsymbol{\hat X}}_{{\rm{opt}}}^{(k + 1)} = \arg \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{X}} {\rm{tr}}({\mathit{\boldsymbol{Q}}^{(k + 1)}}\mathit{\boldsymbol{X}}) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\mathit{\boldsymbol{X}} \geqslant 0,{\mathit{\boldsymbol{X}}_{ii}} = {g_n} \;\; n = 1,2, \cdots ,N \\ \end{array} $$ 3) 利用$\mathit{\boldsymbol{\hat X}}_{{\rm{opt}}}^{(k + 1)}$估计相位误差${\mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}}$，再获取：
$${{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown}} ^{(k + 1)}} = - \angle \mathit{\boldsymbol{\gamma }}_{{\rm{opt}}}^{(k + 1)}$$ 4) 散射系数估计：
$$ {\mathit{\boldsymbol{S}}^{(k + 1)}} = \mathit{\boldsymbol{B}}_e^{(k + 1)}{{\rm{e}}^{ - {\rm{j}}\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown} }}_{}^{^{(k + 1)}}, \;\; n \leftarrow n + 1 $$ end while
返回$\mathit{\boldsymbol{S}} \leftarrow {\mathit{\boldsymbol{S}}^{(k + 1)}}$，${{\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown}} _{{\rm{opt}}}} \leftarrow {\mathop {\mathit{\boldsymbol{\varphi }}}\limits^{\frown}} _{{\rm{opt}}}^{k + 1}$
-
为了验证本文LASAR自聚焦成像算法的有效性，首先利用仿真数据进行分析验证。为了对比文中自聚焦成像算法性能，该节采用了传统相位梯度自聚焦(PGA)算法和文献[11]中半正定松弛自聚焦(autofocusing semidefinite relaxation, AFSDR)算法进行比较，其中PGA算法是针对复图像进行处理。LASAR系统的主要仿真参数如表 1所示。原始仿真场景包含6个点目标，其位置分别为[0, 0, 10] m、[0, 0, -10] m、[10, 0, 0] m、[0, 10, 0] m、[0, -10, 0] m和[-10, 0, 0]m，所有目标散射系数相同且设置为1。
表 1 LASAR系统主要仿真参数
参数 值 中心频域/GHz 37.5 信号带宽/MHz 150 APC总数 4 096 平台高度/m 1 000 采样率/MHz 200 阵列长度/m×m 3×3 为了分析相位误差的影响，对LASAR原始回波数据进行脉冲压缩后，在每一个阵列天线相位中心所对应的数据加入相位误差，其所加相位误差形式为二次项函数或均匀随机分布。而且，为了简便分析，利用函数$P(a)$表示二次项函数$a{x^2}$，$x \in [ - 1,1]$，函数${\rm{U}}(a,b)$表示在区间$[a,b]$上均匀随机分布函数。另外，为了定量评估算法性能，本节利用均方根误差(mean square error, MSE)、图像锐度(image sharpness, IS)和图像熵(image entropy, IE)等3种指标对各算法的成像结果进行判定分析。
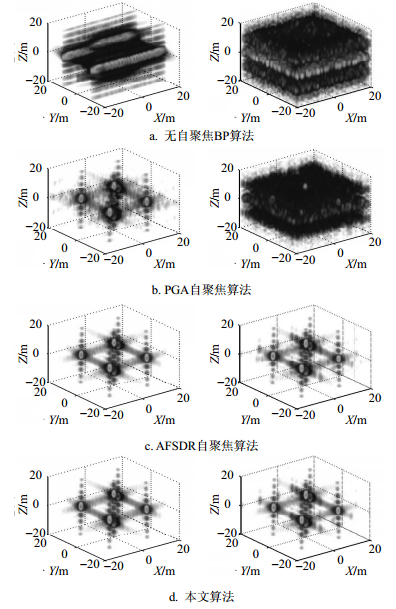
当相位误差形式为二次项函数$P(4,{\rm{\mathsf{π} }} )$和均匀随机分布$U(0,2{\rm{\mathsf{π} }} )$时，图 2分别给出了仿真点目标场景的未自聚焦BP算法、传统PGA自聚焦算法、AFSDR算法和本文算法的LASAR三维成像结果，其中三维图像大小为201×201×201。在该LASAR三维成像结果中，图像显示门限选择为最大值的-25 dB。从图 2成像结果明显可知，受二次项相位误差影响未自聚焦BP算法成像结果存在非常严重的主/旁瓣展宽，受随机相位误差影响其结果存在非常严重的旁瓣串扰，且相位误差越大散焦越严重。利用传统PGA自聚焦算法处理后，在$P(4,{\rm{\mathsf{π} }} )$时点目标聚焦效果得到一定改善，但在$U(0,2{\rm{\mathsf{π} }} )$时自聚焦效果不佳，其与未自聚焦成像结果提升不明显，其原因可能是PGA算法中相位拟合也会导致陡变相位平滑，故对二次项多阶相位误差估计较好，但对于随机相位误差估计效果下降严重。相对于PGA自聚焦，AFSDR自聚焦算法和本文算法成像结果差异较小，均获得了更好的点目标聚焦成像结果，说明本文算法在二次项相位误差影响时可良好地实现LASAR自聚焦成像，而且旁瓣抑制效果优于AFSDR算法，说明本文算法在均匀随机相位误差影响时同样可实现LASAR自聚焦成像。
图 2 仿真点目标成像结果
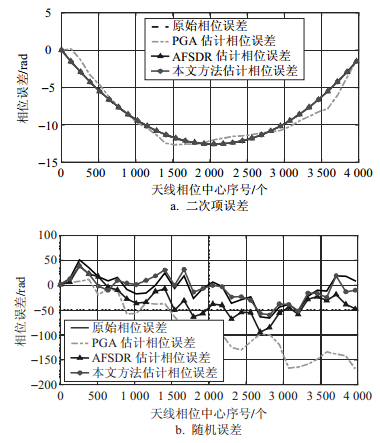
图 3给出了图 2中不同自聚焦算法获得的二次项和随机相位误差估计曲线，其中图 3a为二次项相位误差估计结果，其中原始相位误差、AFSDR算法和本文算法获得的相位基本重合在一起，而PGA算法获得的相位误差与原始相位误差存在一定偏差。图 3b为随机相位误差估计结果，同样可知本文方法获得的相位误差较其他方法更接近真实相位误差。
图 3 相位误差估计结果
为了进一步比较各自聚焦算法性能，在二次项和均匀随机相位误差条件下，利用均方根误差、图像锐度和图像熵等3种指标对各自聚焦算法成像结果进行计算，其结果如表 2所示。无相位误差时BP算法成像结果的指标为${\rm{IS}}({\mathit{\boldsymbol{S}}_0}) = 62.545$和${\rm{IE}}({\mathit{\boldsymbol{S}}_0}) = 1.751 \; 3$。由表 2可知，本文算法的3种指标均明显优于传统PGA自聚焦算法，并且优于AFSDR自聚焦算法，进一步说明了本文算法的有效性。
表 2 仿真数据成像的图像质量指标计算结果
成像方法 指标 二次项相位误差 均匀随机相位误差 P (π) P (2π) P (4π) U (0, π/2) U (0, π) U (0, 2π) 无自聚焦BP MSE 0.963 6 1.216 7 1.273 2 0.653 1 0.853 2 1.077 9 IS 61.576 60.933 60.316 62.136 60.72 3 55.36 5 EN 2.615 7 3.410 1 3.943 0 2.451 8 3.101 9 5.771 1 PGA自聚焦 MSE 0.478 9 0.572 9 0.641 8 0.570 5 0.766 7 1.060 1 IS 62.524 62.082 61.917 62.133 61.126 60.21 0 EN 1.863 6 2.464 0 2.586 7 2.452 2 2.753 5 3.289 0 AFSDR自聚焦 MSE 0.476 5 0.485 1 0.498 1 0.481 7 0.482 7 0.485 5 IS 62.533 62.475 62.435 62.487 62.48 4 62.47 1 EN 1.848 4 2.014 1 2.045 8 2.010 1 2.007 0 2.039 4 本文方法 MSE 0.476 1 0.476 4 0.476 7 0.478 8 0.482 2 0.482 8 IS 62.537 62.489 62.48 7 62.537 62.488 62.48 7 EN 1.843 3 1.999 6 2.004 3 1.845 9 1.989 9 1.996 5 -
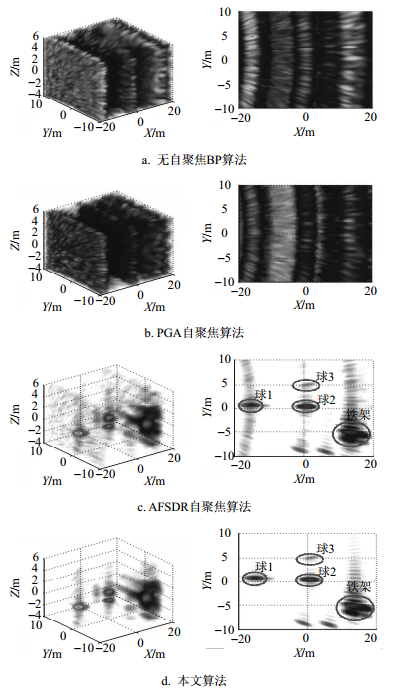
由于没有机载LASAR实测数据，为了验证自聚焦算法性能，该节利用两组地基LASAR实验数据进行验证分析。地基LASAR系统主要参数如下：雷达载频为${f_c} = 9.62{\rm{ GHz}}$，发射信号带宽${B_a} = 120{\rm{ MHz}}$，系统合成的二维阵列尺寸${L_A} \times {L_C} = 1.25{\rm{ m}} \times 1.25{\rm{ m}}$，观测场景中心到系统距离${R_0} = 70{\rm{ m}}$。在数据成像处理时，假设阵列天线运动是匀速运动，但由于实际中天线速度不是恒定的，因此地基LASAR在每一个APC会引入相位误差。另外，为了进一步加大相位误差影响，在每一个APC所对应的数据加入了$U(0,1.5{\rm{\mathsf{π} }} )$分布相位误差。本节两组实验数据对应的观测场景如图 4所示。图 4a是一个孤立点目标场景，主要包含3个定标球和栅栏；图 4b是一个面目标场景，其为施工建筑物的一个大墙面。
图 4 地基LASAR观测场景
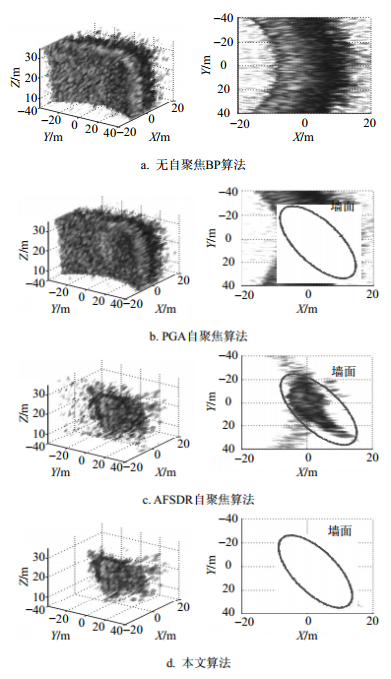
图 5和图 6分别给出了两组地基LASAR观测场景的未自聚焦BP算法、传统PGA自聚焦算法、AFSDR自聚焦算法和本文方法的三维成像结果。图中图像显示门限选择为最大值的-30 dB。从实测数据成像结果可知，在$U(0,1.5{\rm{\mathsf{π} }} )$分布相位误差条件下，未自聚焦BP算法成像结果在3个定标球、栅栏及建筑墙面等目标区域存在非常高的旁瓣，导致目标严重散焦，而且传统PGA自聚焦算法聚集效果提升不大。虽然AFSDR算法较传统PGA自聚焦算法可提供更好的目标聚焦成像，但在目标背景区域中仍然存在一些小的旁瓣串扰，说明AFSDR算法估计的LASAR天线相位中心相位误差不够精确。显然，无论对于孤立点分布的定标球场景还是面结构的建筑墙面场景，本文算法得到的LASAR三维成像结果的旁瓣水平均优于AFSDR算法，其中3个定标球、建筑墙面等目标旁瓣已被抑制。因此，地基LASAR实验数据结果进一步验证了本文算法的有效性。
图 5 定标球场景成像结果(左：三维图像，右：X-Y平面)
图 6 建筑墙面场景成像结果(左：三维图像，右：X-Y平面)
为了定量分析两组LASAR实测数据的自聚焦成像效果，表 3给出了各自聚焦算法图像的图像锐度和图像熵2种指标的计算结果。从表 3可知，本文算法的3种指标均优于传统PGA自聚焦算法和AFSDR自聚焦算法。
表 3 两组地基LASAR实测数据成像的图像质量指标计算结果
成像场景 指标 成像方法 无自聚焦BP PGA自聚焦 AFSDR自聚焦 本文方法 定标球场景 IS 61.332 63.254 68.063 70.218 EN 6.152 9 4.508 5 2.719 3 2.239 2 建筑墙面场景 IS 57.396 57.677 61.43 1 62.79 6 EN 5.864 5 5.824 4 4.261 4 3.559 5 -
本文提出一种基于最大锐度半正定规划的LASAR后向投影自聚焦成像算法。该算法结合LASAR三维图像锐度最大化原则，利用迭代逼近最优方法对LASAR阵列多相位中心的相位误差进行估计。另外，为了提高算法运算效率，仅采用主散射目标区域进行相位误差估计。仿真和实测实验结果显示该算法可适用于任意相位误差形式估计，并且可以提高相位误差的估计精度，提高运动误差条件下LASAR三维成像质量。
Linear Array SAR Autofocus 3-D Imaging via Maximum Sharpness Semidefinite Programming
-
摘要: 线阵合成孔径雷达（LASAR）三维成像技术是一种具有重要潜在应用价值的新型雷达成像技术。但在一个脉冲重复时间中，LASAR系统中需采用阵列天线多个天线相位中心同时接收回波，仅利用载荷单个测量位置的导航测量系统（如惯性测量系统或全球定位系统）数据难以精确补偿LASAR阵列天线多个相位中心的运动误差。为了克服运动误差对阵列多天线相位中心影响，该文提出了一种基于最大锐度半正定规划的LASAR后向投影自聚焦成像算法。该算法建立了后向投影成像算法处理的线性数学模型，结合LASAR三维图像锐度最大化原则，利用迭代逼近最优方法对阵列多天线相位中心运动误差引入的相位误差进行估计。另外，为了提高自聚焦算法运算效率，仅采用主散射目标区域进行相位误差估计。仿真数据和实测数据验证了该算法的有效性。Abstract: Linear array synthetic aperture radar (LASAR) three-dimensional (3-D) imaging technology is a promising innovative 3-D radar imaging technology. As several antenna phase centers (APCs) activity in one pulse repetition time (PRT) simultaneously, it is very difficult to accurately compensate the motion errors of these APCs using navigation measurement data (e.g. inertial measuring unit and global positioning system) only. In this paper, a novel autofocus algorithm is proposed for LASAR 3-D imaging by exploiting maximum sharpness back projection via semidefinite programming. In the scheme, the linear mathematical model of back projection algorithm processing is set up, an iterative method aiming to maximize the LASAR image sharpness is derived to obtain the motion errors of the APCs. Moreover, to improve computational efficacy, only the dominant scatterers are selected as the input of the phase-error estimation. The effectiveness of the algorithm is demonstrated with both simulation and experimental examples.
-
表 1 LASAR系统主要仿真参数
参数 值 中心频域/GHz 37.5 信号带宽/MHz 150 APC总数 4 096 平台高度/m 1 000 采样率/MHz 200 阵列长度/m×m 3×3 
下载: 导出CSV
表 2 仿真数据成像的图像质量指标计算结果
成像方法 指标 二次项相位误差 均匀随机相位误差 P (π) P (2π) P (4π) U (0, π/2) U (0, π) U (0, 2π) 无自聚焦BP MSE 0.963 6 1.216 7 1.273 2 0.653 1 0.853 2 1.077 9 IS 61.576 60.933 60.316 62.136 60.72 3 55.36 5 EN 2.615 7 3.410 1 3.943 0 2.451 8 3.101 9 5.771 1 PGA自聚焦 MSE 0.478 9 0.572 9 0.641 8 0.570 5 0.766 7 1.060 1 IS 62.524 62.082 61.917 62.133 61.126 60.21 0 EN 1.863 6 2.464 0 2.586 7 2.452 2 2.753 5 3.289 0 AFSDR自聚焦 MSE 0.476 5 0.485 1 0.498 1 0.481 7 0.482 7 0.485 5 IS 62.533 62.475 62.435 62.487 62.48 4 62.47 1 EN 1.848 4 2.014 1 2.045 8 2.010 1 2.007 0 2.039 4 本文方法 MSE 0.476 1 0.476 4 0.476 7 0.478 8 0.482 2 0.482 8 IS 62.537 62.489 62.48 7 62.537 62.488 62.48 7 EN 1.843 3 1.999 6 2.004 3 1.845 9 1.989 9 1.996 5
下载: 导出CSV
表 3 两组地基LASAR实测数据成像的图像质量指标计算结果
成像场景 指标 成像方法 无自聚焦BP PGA自聚焦 AFSDR自聚焦 本文方法 定标球场景 IS 61.332 63.254 68.063 70.218 EN 6.152 9 4.508 5 2.719 3 2.239 2 建筑墙面场景 IS 57.396 57.677 61.43 1 62.79 6 EN 5.864 5 5.824 4 4.261 4 3.559 5
下载: 导出CSV
-
[1] KLARE J, BRENNER A, ENDER J. A new airborne radar for 3D imaging-image formation using the ARTINO principle[C]//2006 6th European Conference on Synthetic Aperture Radar (EUSAR). Dresden, Germany: VDE, 2006: 1-4. [2] WEIß M, PETERS O, ENDER J. First flight trials with ARTINO[C]//2008 7th European Conference on Synthetic Aperture Radar (EUSAR). Friedrichshafen, Germany: VDE, 2008: 1-4. [3] WEIß M, GILLES M. Initial ARTINO radar experiments[C]//2010 8th European Conference on Synthetic Aperture Radar (EUSAR). Aachen, Germany: VDE, 2010: 1-4. [4] WEI Shun-jun, ZHANG Xiao-ling, SHI Jun. Linear array SAR imaging via compressed sensing[J]. Progress in Electromagnetics Research, 2011, 117:299-319. doi: 10.2528/PIER11033105 [5] WEI Shun-jun, ZhANG Xiao-ling, SHI Jun, et al. Sparse array microwave 3-D imaging:Compressed sensing recovery and experimental study[J]. Progress in Electromagnetics Research, 2013, 135:161-181. doi: 10.2528/PIER12082305 [6] PENG X, HONG W, WANG Y, et al. Polar format imaging algorithm with wave-front curvature phase error compensation for airborne DLSLA three-dimensional SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6):1036-1040. doi: 10.1109/LGRS.2013.2282335 [7] SHI Jun, ZHANG Xiao-ling, YANG Jian-yu, et al. APC trajectory design for 'One-Active' linear-array three-dimensional imaging SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3):1470-1486. doi: 10.1109/TGRS.2009.2031430 [8] WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3):827-835. doi: 10.1109/7.303752 [9] MORRISON R L, MINH N D, DAVID C M. SAR image autofocus by sharpness optimization:a theoretical study[J]. IEEE Transactions on Image Processing, 2007, 16(9):2309-2321. doi: 10.1109/TIP.2007.903252 [10] ASH J N. An autofocus method for back projection imagery in synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1):104-108. doi: 10.1109/LGRS.2011.2161456 [11] LIU K H, WIESEL A, DAVID C M. Synthetic aperture radar autofocus via semidefinite relaxation[J]. IEEE Transactions on Image Processing, 2013, 22(6):2317-2326. doi: 10.1109/TIP.2013.2249084 [12] WEI S J, ZHANG X L, SHI J. An autofocus approach for model error correction in compressed sensing SAR imaging[C]//2012 IEEE International Geoscience and Remote Sensing Symposium.[S.l.]: IEEE, 2012: 3987-3990. [13] WEI S J, ZHANG X L. Sparse autofocus recovery for under-sampled linear array SAR 3-D imaging[J]. Progress in Electromagnetics Research, 2013, 140:43-62. doi: 10.2528/PIER13020614 [14] WEI S J, ZHANG X L, SHI J. Sparse autofocus via Bayesian learning iterative maximum and applied for LASAR 3-D imaging[C]//2014 IEEE Radar Conference.[S.l.]: IEEE, 2014: 666-669. [15] CETIN M, STOJANOVIC I, ONHON O, et al. Sparsity-driven synthetic aperture radar imaging:Reconstruction, autofocusing, moving targets, and compressed sensing[J]. IEEE Signal Processing Magazine, 2014, 31(4):27-40. doi: 10.1109/MSP.2014.2312834 -
点击查看大图
图(6) / 表(3)
计量
- 文章访问数: 5522
- HTML全文浏览量: 1875
- PDF下载量: 139
- 被引次数: 0
