IP Network Congested Link Location Algorithm Based on Bayesian Network
-
摘要: 在借助E2E路径性能主动探测技术进行内部拥塞链路推理的网络层析成像方法中,传统的利用路径探测计算链路丢包率的方法涉及线性方程组求逆,其计算量过大可能导致算法失效。对此,该文提出一种基于布尔代数的IP网络拥塞链路定位算法,通过对求解先验概率的线性方程组构造满秩系数矩阵,从而计算出各链路拥塞先验概率,再借助贝叶斯最大后验概率算法推理定位当前时刻拥塞链路集合。实验验证了该算法的有效性及准确性。Abstract: In the method of end-to-end (E2E) path performance active detection (network tomography), the link loss rate solution methods involve the inverse of linear equations, so its large computation complexity may lead to failure. This paper proposes a new congestion link location algorithm based Boolean model. First the nonsingular coefficient matrix of the linear system for solving prior probability is formed; then the prior probability of link congestion is calculated. Finally, based on Bayesian maximum a posteriori probability (MAP) estimator, the set of congested links can be located. The validity and accuracy of this algorithm is verified by experiments.
-
Keywords:
- Bayesian MAP /
- Boolean model /
- congested link location /
- IP network
-
如何在网络中进行快速故障定位进而保障业务的正常运作,成为IP网络故障管理的核心问题。根据端到端的测量来推断内部链路特性的方法被称为网络Tomography方法,并根据求解方式不同分为两类:第一类需要在广播探测数据包之间存在很强的时间相关性[1-2],并进行矩阵求逆;第二类利用解决布尔代数求逆的方法推导网络中拥塞链路的分布[3-4]。在第一类中,文献[5-6]利用发送多播探测数据包的方法推算网络链路丢包率,但受到现实网络中支持多播路由器的数量限制。此类方法与多播副本相比准确率较低,开发和管理的费用却很高;同时计算链路丢包率的迭代算法应用于大规模网络中的实时代价过高。在第二类方法中则是采用不相关的端到端测量值来识别拥塞链路。这里通常要假设所有链路具有相同的拥塞先验概率${P_0}$,且${P_0}$比较小。但在实际网络环境中,每个链路具有的拥塞概率不可能都相同,且当${P_0}$较大时此类算法的结果也比较差[4]。文献[7]利用ICMP回送请求来推断丢包率,但由于安全和性能等原因使得许多路由器限制了对该类请求的反映,因此实时性较差。
针对以上问题,本文使用一段时间内多个快照求路径丢包率,再利用一种基于贝叶斯网络的拥塞链路定位算法 (Bayesian network–based congested link position algorithm, BNCLPA) 获得链路拥塞先验概率,然后在下一次快照中使用最大后验估计 (MAP) 寻找拥塞链路。
1. 网络和性能模型
1.1 网络建模
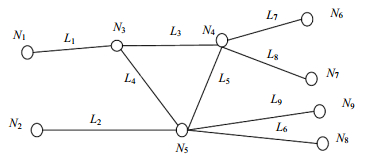
首先,利用贝叶斯网络模型有向图${\boldsymbol{g}} = ({\boldsymbol{\nu }}, \boldsymbol{\varepsilon} )$对拥塞链路集合定位问题进行建模。其中,${\boldsymbol{\nu }}$表示网络中的节点,$\boldsymbol{\varepsilon }$表示节点间的通信链路,数量分别为${n_\nu } = |{\boldsymbol{\nu }}|$和${n_e} = |\boldsymbol{\varepsilon} |$;${{\boldsymbol{V}}_{\boldsymbol{B}}}$表示所有优势点的集合且${n_B}$为其中的点数,${\boldsymbol{P_{s, t}}}$为从源点s到目的节点t所经过的路径,表示优势点之间路径的集合且其中的路径数为${n_P} = {n_B}({n_B}-1) = |\boldsymbol{P}|$。对于一个已知的${\boldsymbol{g}} = ({\boldsymbol{\nu }}, \boldsymbol{\varepsilon} )$和P,按照下述方法计算选路矩阵$\boldsymbol{D}({n_P} \times {n_e})$:若路径${{\boldsymbol{P}}_{\boldsymbol{i}}}$包含链路${\boldsymbol{e}_j}$则${\boldsymbol{D}_{ij}} = 1$,否则${\boldsymbol{D}_{ij}} = 0$。D的一行对应一条路径,一列对应一条链路。若D的某一列为全零,则丢弃这些列得到矩阵$\boldsymbol{D}({n_P} \times {n_c})$,${n_c}$表示非零链路的数量且${n_c} \le {n_e}$。${\boldsymbol{\varepsilon }_c}$表示至少被P中的一条路径所包含的链路集合且$|{\boldsymbol{\varepsilon }_c}| = {n_c}$。图 1所示的IP网络共有9个节点和9条链路,其中节点1和2为源节点,节点6~8为目的节点,路径与链路的对应关系如表 1所示。
表 1 路径与链路关系路径Ps-t 链路 P1-6 L1→L3 → L7 P1-7 L1→L3 → L8 P1-8 L1→L4 → L6 P2-6 L2→L5 → L7 P2-7 L2→L5 → L8 P2-8 L2→L6 根据表 1可以得到选路矩阵为:
$$\boldsymbol{D}({n_P} \times {n_e}) = \left[{\begin{array}{*{20}{c}} 1&0&1&0&0&0&1&0&0\\ 1&0&1&0&0&0&0&1&0\\ 1&0&0&1&0&1&0&0&0\\ 0&1&0&0&1&0&1&0&0\\ 0&1&0&0&1&0&0&1&0\\ 0&1&0&0&0&1&0&0&0 \end{array}} \right]$$ (1) 由于L9为全零列,将$\boldsymbol{D}({n_P} \times {n_e})$化简为:
$$\boldsymbol{D}({n_P} \times {n_c}) = \left[{\begin{array}{*{20}{c}} 1&0&1&0&0&0&1&0\\ 1&0&1&0&0&0&0&1\\ 1&0&0&1&0&1&0&0\\ 0&1&0&0&1&0&1&0\\ 0&1&0&0&1&0&0&1\\ 0&1&0&0&0&1&0&0 \end{array}} \right]$$ (2) 1.2 性能建模
若已知网络拓扑和端到端的路径丢包率,则链路丢包率和路径丢包率之间为线性关系:
$$\log ({\phi _i}) = \sum\limits_{k = 1}^{{n_c}} {\log ({\phi _{{e_k}}})} {\boldsymbol{D}_{ik}}$$ (3) 式中,${\phi _i}$表示路径${\boldsymbol{P}_i}$的传输率;${\phi _{{e_k}}}$表示链路${\boldsymbol{e}_k}$的传输率。为了确定链路的传输率,需要求解式 (3)。由于许多网络中的D不是满秩矩阵,即其秩$r(\boldsymbol{D}) < \min ({n_P}, {n_c})$,所以式 (3) 的解不唯一。
本文的目的是识别拥塞链路,因此可以做以下改进:阈值${t_{\rm{l}}}$表示根据应用程序指定的极限值,当${\phi _{{e_k}}} \ge {t_{\rm{l}}}$时认为链路${\boldsymbol{e}_k}$是连通的,否则链路${\boldsymbol{e}_k}$就是拥塞的;变量${y_i}$表示路径${\boldsymbol{P}_i}$的状态,当${\boldsymbol{P}_i}$是通的${y_i} = 0$,当${\boldsymbol{P}_i}$是拥塞的${y_i} = 1$;变量${x_k}$表示链路${\boldsymbol{e}_k}$的状态,当${\boldsymbol{e}_k}$是通的${y_i} = 0$,当${\boldsymbol{e}_k}$是拥塞的${x_k} = 1$。
建立一个布尔线性代数方程组:
$${\boldsymbol{y}_i} = \rm{V}_{k = 1}^{{n_c}}{x_k} \cdot {\boldsymbol{D}_{ik}}$$ (4) 式中,‘V’表示二进制最大操作;‘·’表示通常的乘法操作。式 (4) 可以用向量表示为:
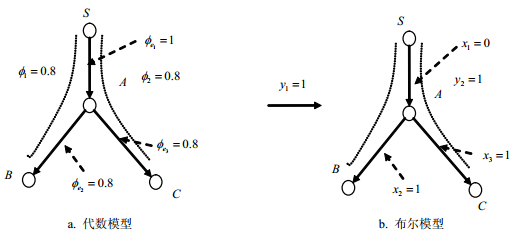
$$\boldsymbol{y} = V_{k = 1}^{{n_c}}{x_k} \cdot {\boldsymbol{d}_k}$$ (5) 式中,${\boldsymbol{d}_k}$表示矩阵D的第k个列向量。图 2说明了从线性代数到布尔代数的转换。图中${\boldsymbol{e}_1} = SA$是好的链路且${\phi _{{e_1}}} = 1$,${e_2} = AB$及${e_3} = AC$都是拥塞链路且${\phi _{{e_2}}} = 0.8$、${\phi _{{e_3}}} = 0.8$。令${t_1} = 0.9$,则${t_p} = {0.9^2} = 0.81$,路径${\boldsymbol{P}_1}$(S到B) 和${\boldsymbol{P}_2}$(S到C) 都是拥塞的。
在布尔代数中,路径传输率和链路传输率之间是线性关系,而链路状态和路径状态也呈线性关系。一般来说,当且仅当D的所有列在布尔代数中都线性无关时此方程才有唯一的解,但实际中很难满足。因此,需要利用网络中链路的其他信息来找到式 (4) 最有可能的解。首先,用向量${\boldsymbol{p}} = {[{p_1}, {p_2}, \cdots, {p_{{n_c}}}]^{\rm{T}}}$表示链路状态概率,在理论上可以从端到端的测量中获得p。本文提出了一种利用BNCLP算法从较少的快照中估算p,再把p作为一个链路状态的先验概率,利用已知信息寻求确定真正拥塞链路的方法。
2. BNCLPA算法
BNCLPA算法的原理框图如图 3所示。
2.1 先验概率学习
首先,设链路概率向量为p,检测网路链路集合的概率为${P_p}$,X是${n_c}$维随机二进制向量,Y为${n_P}$维随机二进制向量。若链路状态概率满足对任何y有${P_p}(\boldsymbol{Y} = \boldsymbol{y}) = {P_{\tilde p}}(\boldsymbol{Y} = \boldsymbol{y})$,则$\boldsymbol{p} = \boldsymbol{\tilde p}$。为了避免传统方法中使用最大期望 (expectation-maximization, EM) 算法求解p时的计算代价过高且不具备全局收敛性的问题,本文利用数学期望求解的方法对式 (4) 进行推导,求出链路x的概率值。
对所有$1 \le i \le {n_p}$,有:
$$\begin{array}{c} {E_p}[{\boldsymbol{Y}_i}] = 1 -{P_p}({\boldsymbol{X}_k}{\boldsymbol{D}_{ik}} = 0, 1 \le k \le {n_c}) = \\ 1 -\prod\limits_{k = 1}^{{n_c}} {(1 -{\boldsymbol{p}_k})} \end{array}$$ (6) 由于$r(\boldsymbol{D}) < \min ({n_p}, {n_c})$,所以需通过高阶矩阵空间相关特性提供更多的信息。定义${\boldsymbol{Y}_{ij}}$为二进制随机变量,当路径i及j正常时${\boldsymbol{Y}_{ij}} = 0$,否则${\boldsymbol{Y}_{ij}} = 1$,则:
$$\begin{gathered} {E_p}[{\boldsymbol{Y}_{ij}}] = \\ {P_p}(V_{k = 1}^{{n_c}}{\boldsymbol{X}_k}{\boldsymbol{D}_{ik}} = 1) \cup {P_p}(V_{k = 1}^{{n_c}}{\boldsymbol{X}_k}{\boldsymbol{D}_{ik}} = 1) = \\ 1 -\prod\limits_{k = 1}^{{n_c}} {{{(1 -{\boldsymbol{p}_k})}^{{\boldsymbol{D}_{ik}} \vee {\boldsymbol{D}_{jk}}}}} \\ \end{gathered} $$ (7) 对所有满足$1 \leqslant i \leqslant j \leqslant {n_p}$的 (i, j) 对,定义:
$${\boldsymbol{y}^{(1)}} = {[-\lg (1-{\boldsymbol{y}_1})-\lg (1 - {\boldsymbol{y}_2}) - \cdots - \lg (1 - {\boldsymbol{y}_{{n_p}}})]^{\text{T}}}$$ (8) $$\begin{gathered} {\boldsymbol{y}^{(2)}} = \\ \left[{-\lg \left( {1-{{\boldsymbol{y}}_{12}}} \right)-\lg \left( {1 - {\boldsymbol{y}_{22}}} \right) - \cdots - \lg {{\left( {1 - {\boldsymbol{y}_{({n_p} - 1), {n_{p/2}}}}} \right)}^{\text{T}}}} \right] \\ \end{gathered} $$ (9) $$\begin{gathered} - \lg (1- \boldsymbol{p}) = \\ {[-\lg (1-{\boldsymbol{p}_1})-\lg (1 - {\boldsymbol{p}_2}) - \cdots - \lg (1 - {\boldsymbol{p}_{{n_c}}})]^{\text{T}}} \\ \end{gathered} $$ (10) 结合式 (6) 和式 (7) 系统线性方程组为:
$$\left[\begin{gathered} {\boldsymbol{y}^{(1)}} \hfill \\ {\boldsymbol{y}^{(2)}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} {\boldsymbol{D}^{(1)}} \hfill \\ {\boldsymbol{D}^{(2)}} \hfill \\ \end{gathered} \right]{( -\lg (1 -\boldsymbol{p}))^{\text{T}}}$$ (11) 由此可构造满秩矩阵。在实际网络中可以化简选路矩阵来减少求解式 (11) 的计算复杂度。如图 1所示的IP网络,若根据m次快照测得${y_a} = 0$,则L1、L4、L6全部为通的,把式 (2) 中的矩阵D进行化简得到:
$${{\boldsymbol{D}}_1} = \left[{\begin{array}{*{20}{c}} 0&1&0&1&0 \\ 0&1&0&0&1 \\ 1&0&1&1&0 \\ 1&0&1&0&1 \\ 1&0&0&0&0 \end{array}} \right]$$ (12) 然后进行初等行变换得到:
$${{\boldsymbol{D}}_2} = \left[{\begin{array}{*{20}{c}} 1&0&0&0&0 \\ 0&1&0&1&0 \\ 0&0&1&1&0 \\ 0&0&0&{-1}&1 \\ 0&0&0&0&0 \end{array}} \right]$$ (13) 根据${{\boldsymbol{D}}_1}$和${{\boldsymbol{D}}_2}$得到最大线性无关组组成矩阵为:
$${\boldsymbol{D}_3} = \left[{\begin{array}{*{20}{c}} 0&1&0&1&0 \\ 0&1&0&0&1 \\ 1&0&1&1&0 \\ 1&0&0&0&0 \end{array}} \right]$$ (14) ${{\boldsymbol{D}}_3}$即式 (13) 中的D[1]。将${{\boldsymbol{D}}_3}$进行最大化操作得到:
$${\boldsymbol{D}_4} = \left[{\begin{array}{*{20}{c}} 0&1&0&1&1 \\ 1&1&1&1&0 \\ 1&1&0&1&0 \\ 1&1&1&1&1 \\ 1&1&0&0&1 \\ 1&0&1&1&0 \end{array}} \right]$$ (15) 从${\boldsymbol{D}_4}$中选出一行加入到${\boldsymbol{D}_3}$中,形成的满秩矩阵${\boldsymbol{D}_5}$,即为式 (13) 所需满秩矩阵:
$${\boldsymbol{D}_5} = \left[{\begin{array}{*{20}{c}} 0&1&0&1&0 \\ 0&1&0&0&1 \\ 1&0&1&1&0 \\ 1&0&0&0&0 \\ 0&1&0&1&1 \end{array}} \right]$$ (16) 而对于式 (13),选择${\boldsymbol{D}_2}$第一行与${\boldsymbol{D}_3}$构成一个满秩矩阵,得到式 (11) 中${\boldsymbol{D}^{(2)}} = [\begin{array}{*{20}{c}} 0&1&0&1&1 \end{array}]$,${\boldsymbol{y}^{(2)}} =-\lg (1-{\boldsymbol{y}_{12}})$。通过对$\left[\begin{gathered} {\boldsymbol{D}^{(1)}} \hfill \\ {\boldsymbol{D}^{(2)}} \hfill \\ \end{gathered} \right]$取逆可求得链路的先验概率p。而在${n_c}$这条链路中,未参与式 (11) 计算的链路的概率值为0。
2.2 拥塞链路定位算法
设定已知信息选路矩阵为$\boldsymbol{D}({n_p} \times {n_c})$,网络中${n_p}$条路径最近一次快照值为Y,已求得链路状态的先验概率为P。首先,定义最大评分参量$\arg {\max _x}{P_\boldsymbol{p}}(\boldsymbol{X} = \boldsymbol{x}|\boldsymbol{Y} = \boldsymbol{y})$为拥塞链路集合的最大后验估计,${P_\boldsymbol{p}}( \cdot )$为条件概率,则由贝叶斯公式可得:
$$\begin{gathered} {P_{_\boldsymbol{x}^\boldsymbol{p}}}(\boldsymbol{X} = \boldsymbol{x}|\boldsymbol{Y} = \boldsymbol{y}) = \\ \frac{{{P_\boldsymbol{p}}(\boldsymbol{Y} = \boldsymbol{y})|(\boldsymbol{X} = \boldsymbol{x}){P_\boldsymbol{p}}(\boldsymbol{X} = \boldsymbol{x})}}{{{P_\boldsymbol{p}}(\boldsymbol{Y} = \boldsymbol{y})}} \\ \end{gathered} $$ (17) 式中,${P_\boldsymbol{p}}(\boldsymbol{Y} = \boldsymbol{y})$仅依赖网络状态检测,与x的选择无关,故最大评分参量可表示为:
$$\arg {\max _x}{P_\boldsymbol{p}}(\boldsymbol{Y} = \boldsymbol{y}|\boldsymbol{X} = \boldsymbol{x}){P_\boldsymbol{p}}(\boldsymbol{X} = \boldsymbol{x})$$ (18) 由于链路状态${x_k}$是独立随机变量,则:
$${P_{_x^p}}(X = x) = \prod\limits_{k = 1}^{{n_c}} {p_k^{{x_k}}} {(1-{p_k})^{(1-{x_k})}}$$ (19) 在给定$\boldsymbol{X} = \boldsymbol{x}$,${\boldsymbol{Y}_i} = 0$且${\boldsymbol{D}_{ik}}{x_k} = 0$或等价于$(1-{\boldsymbol{D}_{ik}}){x_k} = 1$时,有:
$$\begin{gathered} {P_p}(\boldsymbol{Y} = \boldsymbol{y})|(\boldsymbol{X} = \boldsymbol{x}) = \\ \prod\limits_{{{\boldsymbol{P}}_i} \in {P_c}} {({\boldsymbol{Y}_i} = 0|\boldsymbol{X} = 0)} {P_p}\prod\limits_{{{\boldsymbol{P}}_i} \in {P_c}} {({\boldsymbol{Y}_i} = 1|\boldsymbol{X} = \boldsymbol{x}){P_p}} \\ \end{gathered} $$ (20) 可知概率为1或者0。定义R为从D[1]中移除所有正常路径行以及其对应链路的所有列,${\varepsilon _R}$是R中列的集合,那么对于链路集合$\boldsymbol{\chi} \in {\varepsilon _R}$,所有的拥塞路径至少覆盖一条链路在$\boldsymbol{\chi }$中,有:
$$\begin{array}{c} \arg {\max _{\boldsymbol{x} \subseteq {\varepsilon _R}}}{P_p}({\bf{\chi }}) = \\ \arg {\max _{\boldsymbol{x} \subseteq {\varepsilon _R}}}\prod\limits_{k = 1}^{\left| {{\boldsymbol{\varepsilon }_\boldsymbol{R}}} \right|} {{{(1 - {\boldsymbol{p}_k})}^{(1 - {x_k})}}} p_{{\boldsymbol{p}_k}}^{{x_k}} \end{array}$$ (21) 取对数再移除与x的取值无关的项得到:
$$\arg \mathop {\max }\limits_{\boldsymbol{x} \subseteq {\varepsilon _R}} {P_\boldsymbol{p}}(\boldsymbol{\chi }) = \arg \mathop {\min }\limits_{\boldsymbol{x} \subseteq {\varepsilon _R}} \sum\limits_{k = 1}^{\left| {{\varepsilon _R}} \right|} {{x_k}\lg \frac{{1-{\boldsymbol{p}_k}}}{{{\boldsymbol{p}_k}}}} $$ (22) 式中,$\sum\limits_{k = 1}^{\left| {{\varepsilon _R}} \right|} {{\boldsymbol{R}_{ik}}} {x_k} \geqslant 1$且$1 \leqslant i \leqslant \left| {{P_c}} \right|$。
3. 仿真实验及结果分析
对于主动探测技术,网络拓扑在很大程度上影响了探测结果,从而影响到故障诊断的结果。Brite[8]拓扑产生器是网络仿真实验中常用的网络拓扑生成工具,它可以生成3种网络拓扑模型Waxman[9]、BA[10]和GLP[11]。其中BA模型和GLP模型都是幂率类型,而GLP模型更接近于实际网络的结构特征,可以较准确地模拟真实IP网的拓扑情况。因此,本文采用Brite产生的GLP模型来进行仿真实验。
在仿真实验中,需要在不同的网络拥塞层次下对算法进行评价。本文使用丢包模型LM1[4],其中拥塞链路的丢包率分布在0.05~1之间,好链路的丢包率在0~0.01之间。每条链路都有一个指定的丢包率,所以每条链路的实际丢包都遵循Gilbert过程,链路的状态在不丢失任何数据包与丢失所有的数据包之间来回波动。
本文利用Java语言中的Eclipse开发平台模拟端到端到探测、拥塞事件及算法推理。在求解链路拥塞概率${{\boldsymbol{p}}_k}$时,考虑到式 (13) 中的系数矩阵是一个稀疏矩阵,采用迭代法来求解。同时,在求解${{\boldsymbol{p}}_k}$时实现Java程序对Matlab程序的调用,以更方便有效地得到计算结果。
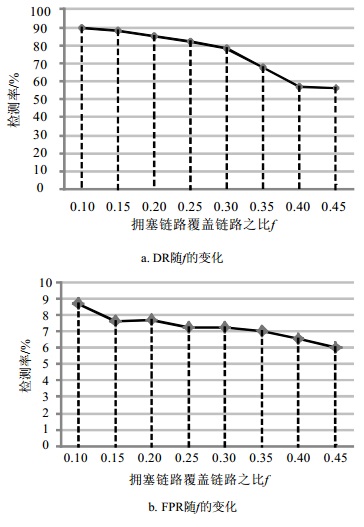
1) 拥塞率f对DR和FPR的影响。由Brite拓扑生成器产生100个节点的拓扑,拥塞链路的百分比$f \in [0.1, 0.45]$,步长为0.05,连接某节点的总链路数d=7,学习先验概率时的快照次数m=40,拥塞链路的门限值t=0。从图 4中可以看出,随着f的增加,算法的检测率DR和误检率FPR会越来越低。
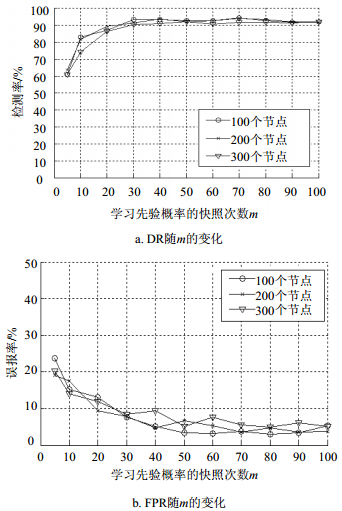
2) 快照次数m对DR和FPR的影响。拓扑规模分别为100、200和300个节点,m在5~100之间变化,d=7,f=0.1,t=0。从图 5中可以看出:当m < 30时,DR较低而FPR较高,说明快照次数太少无法准确得到链路的先验拥塞概率,导致算法的DR较低而FPR较高,因此在推断网络故障时快照次数不能低于30;但是m并不是越大越好,若m过大如超过40后,DR并不会继续升高而FPR也不会降低,同时主动测试时发包数量过多会导致网络负载增加、时间成本过大,影响算法的时效性。因此,在学习链路的先验拥塞概率时,应使$30 \leqslant m \leqslant 40$。
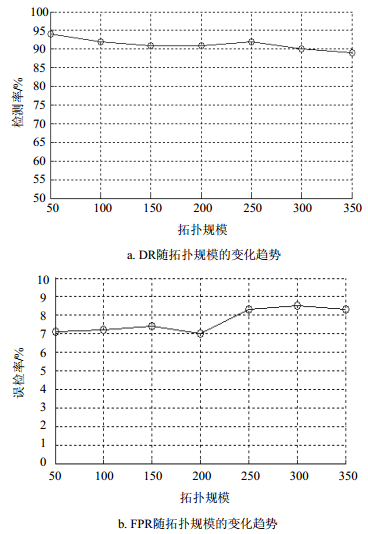
3) 拓扑规模对DR和FPR的影响。生成的网络拓扑规模在50~350之间变化,f=0.1,t=0,d=7,m=30。从图 6可以看出:DR随着拓扑规模的增大而呈下降趋势,并在一定的范围内有所波动,但是下降的幅度不大,速度也不是很快;而FPR随着拓扑规模的增大,而呈上升趋势,并在一定的范围内有所波动,但是上升的幅度不大,且上升的速度也不是很快。这说明BNPDA算法对拓扑规模的变化具有较好的稳定性。
4. 结束语
针对现有方法在网络链路故障诊断方面的不足,本文提出了一种基于贝叶斯网的故障诊断算法BNPDA。该方法采用主动测量方式测量网络端到端的性能,需要在被测网络中部署探针硬件设备;同时主动测量时所发的探测包也会在网络中产生新的流量,增加网络负载。如何在达到监测网络的情况下,尽量减少探针的部署和探针的发包数量,以减少对网络的影响以及监测系统的维护代价,同时获取更多的网络信息是今后研究的重点之一。
-
表 1 路径与链路关系
路径Ps-t 链路 P1-6 L1→L3 → L7 P1-7 L1→L3 → L8 P1-8 L1→L4 → L6 P2-6 L2→L5 → L7 P2-7 L2→L5 → L8 P2-8 L2→L6 -
[1] OGINO N, KITAHARA T, ARAKAWAET S, et al. Decentralized Boolean network tomography based on network partitioning[C]//In NOMS'16: IEEE/IFIP Network Operations and Management Symposium. Istanbul: IEEE, 2016: 162-170.
[2] DENG K, LI Y, ZHU W, et al. Fast parameter estimation in loss tomography for networks of general topology[J]. The Annals of Applied Statistics, 2016, 10(1): 144-164. DOI: 10.1214/15-AOAS883
[3] DUFFIELD N G. Network tomography of binary network performance characteristics[J]. IEEE Trans on Information Theory, 2006, 52(12): 5373-5388. DOI: 10.1109/TIT.2006.885460
[4] BATSAKIS A, MALIK T, TERZIS A. Practical passive lossy link inference[C]//Proc of PAM 2005: 6th International Workshop. Boston: Springer Berlin Heidelberg, 2005, 3431: 362-367.
[5] NGUYEN H X, THIRAN P. The Boolean solution to the congested IP link location problem: Theory and practice[C]//Proceedings of IEEE INFOCOM'07: 26th Annual IEEE Conference on Computer Communications. Alaska: IEEE, 2007: 2117-2125.
[6] DUFFIELD N G, PRESTI F L, PAXSON V, et al. Inferring link loss using striped unicast probes[C]//Proceeding of the IEEE INFOCOM'01: Conference on Computer Communications. [S.l.]: IEEE Communications Society, 2001: 915-923.
[7] MAHAJAN R, SPRING N, WETHERALL D, et al. User-level internet path diagnosis[C]//Proceedings of the 19th ACM Symposium on Operating Systems Principles. New York: ACM, 2003: 106-119.
[8] MEDINA A, LAKHINA A, MATTA I, et al. BRITE: an approach to universal topology gerneration[C]//Proceedings of MASCOTS: Proceedings Ninth International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems. Washington: IEEE, 2001: 346-353.
[9] WAXMAN B M. Routing of multipoint connections[J]. IEEE Journal of Selected Areas in Communication, 1988, 6(9): 1617-1622. DOI: 10.1109/49.12889
[10] BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI: 10.1126/science.286.5439.509
[11] PALMER C R, STTEFFAN J G. Generating network topologies that obey power laws[C]//Proc of the GLOBECOM 2000: Global Telecommunications Conference. San Francisco: IEEE, 2000: 434-438.
-
期刊类型引用(2)
1. 张人杰,胡超,刘威. 空间延迟容忍网络中多链路数据拥塞控制算法. 吉林大学学报(工学版). 2020(04): 1472-1477 .  百度学术
百度学术
2. 刘玉敏,王立中,郭彬. 网络综合布线链路稳定性实时检测仿真研究. 计算机仿真. 2018(12): 355-358 .  百度学术
百度学术
其他类型引用(2)

 ISSN
ISSN 


 下载:
下载: