Research on a Power Distribution Stability Control Strategy of Hybrid Energy Storage System in Vehicles
-
摘要: 针对混合动力电动汽车蓄电池-超级电容器复合电源功率分配问题,提出了一种基于滑模变结构和李雅普诺夫的稳定控制策略。滑模变结构控制策略的控制目标包括稳定直流母线电压和精确跟踪超级电容器电流参考值。同时,基于李雅普诺夫理论,对闭环控制系统进行了稳定性分析。在ADVISOR仿真环境下进行仿真研究,并搭建实验样机,进行实验研究。仿真和实验结果表明,该复合电源功率分配控制策略能很好地实现两个控制目标,控制系统实现全局渐近稳定。Abstract: A synovial variable structure and Lyapunov power distribution stability control strategy of hybrid energy storage system (HESS) in hybrid electric vehicles (HEV) is presented. The strategy aims to control power converters based on the synovial variable structure in order to satisfy the following requirements:stabilized dc bus voltage regulations and perfectly tracked of SC current to its reference. At the same time, the stability of the closed-loop control system based on the Lyapunov theory is analyzed. The HESS and control strategy are modeled and simulated under the ADVISOR simulation environment, and a prototype of HESS is also built. The results show that the designed control strategy meets all the objectives and achieves asymptotic stability of the closed loop system.
-
现在,国内外学者对未来汽车进行了大量的研究,混合动力电动汽车以其绿色环保、节能和动力性能良好等优势被认为是一种最佳的解决方案[1]。目前,大多数混合动力电动汽车配置两种储能装置,一种储能装置具有高能量密度,称为“主电源”,通常采用蓄电池;另一种储能装置具有高功率密度和可逆性,称为“辅助电源”,通常采用超级电容器。主电源主要负责汽车长时间的续航,而辅助电源主要负责汽车瞬时加速和再生制动能量回收[2]。蓄电池与超级电容器相结合构成复合电源,超级电容器和蓄电池优势互补,会大大提高汽车能量存储系统的性能[3]。
要实现蓄电池、超级电容器和负载三者之间能量和功率的动态转移,需要利用功率变换器的主动变流技术来实现,通过主动控制功率变换器,实现蓄电池和超级电容之间功率的合理分配,满足负载能量和功率的双重需求[4]。
复合电源功率分配控制策略可归纳总结为两类:线性控制策略和非线性控制策略。对于线性控制策略,其工作原理是将汽车需求功率与蓄电池和超级电容器的荷电状态进行线性化分配[5],控制规则简单易实现。但是由于复合电源系统属于非线性系统,采用线性控制策略控制非线性系统其控制稳定性不强[6]。对于非线性控制策略,包括神经网络控制[7]、模糊控制[8]和自适应控制[9]等,其控制效果各有利弊。但目前大多数复合电源功率分配控制策略缺乏对其控制系统稳定性的分析,系统不稳定,控制策略实际应用价值不大。
本文设计了一种基于滑模变结构和李雅普诺夫的复合电源功率分配稳定控制策略,经过仿真和实验验证发现,该控制策略在满足所设计的控制目标的基础之上,控制系统可实现全局渐进稳定。
1. 滑模变结构控制策略设计
复合电源拓扑结构见图 1,在文献[10]中对复合电源进行了详细的建模,包括局部模块建模和全局系统建模。基于此,本文设计的滑模变结构控制策略包括两个控制目标:1)稳定直流母线电压;2)精确跟踪超级电容器电流参考值。
由于Boost变换器不可逆[11],本文不直接控制直流母线电压$ {v_{{\rm{dc}}}} $跟踪其参考值$ {v_{{\rm{dc}} - {\rm{ref}}}} $,而是间接控制方法,即:$ {i_{{\rm{bf}}}} $跟踪其参考值$ {i_{{\rm{bf}} - {\rm{ref}}}} $。当系统达到稳定状态时,存在$ {i_{{\rm{bf}}}} = {i_{{\rm{bf}} - {\rm{ref}}}} $,${v_{{\rm{dc}}}} = {v_{{\rm{dc}} - {\rm{ref}}}} $,$ {v_{{\rm{dc}} - {\rm{ref}}}} > {v_b} $。根据功率守恒原则得到:
$$ {i_{{\rm{bf}} - {\rm{ref}}}} = \lambda \left( {\frac{{{v_{{\rm{dc}} - {\rm{ref}}}} - {v_{{\rm{uc}} - {\rm{ref}}}}}}{{{v_b}}}} \right) $$ (1) 式中,$ \lambda \ge 1 $,定义为损耗因子,包含电感损耗和开关损耗;$ {v_{{\rm{uc}} - {\rm{ref}}}}$为超级电容器端电压${v_{{\rm{uc}}}} $的参考值。
为实现两个控制目标,采用滑模变结构控制策略,引入滑动面表现为:
$$ \mathit{\boldsymbol{S}} = {[{s_1}, {s_2}]^{\rm{T}}} $$ (2) 其中,有:
$$ {s_1} = {x_1} - {i_{{\rm{bf}} - {\rm{ref}}}} $$ (3) $$ {s_2} = {x_2} - {i_{{\rm{uc}} - {\rm{ref}}}} $$ (4) $ {x_1} $为$ {i_{{\rm{bf}}}}$的平均值;$ {x_2} $为$ {i_{{\rm{uc}}}} $的平均值。
因此,控制目标转换为确保系统滑动面$ S = 0 $。当一个控制目标实现后,系统被定义为在一个滑动模式$\dot S $下。在这种情况下,所谓的不变条件可表示为:
$$ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{\dot S}} = 0 $$ (5) 所以,全局控制信号$ {u_1}$和$ {u_{23}} $的等效控制信号函数可改写为:
$$ {\mu _{1{\rm{eq}}}} = 1 + \frac{{{L_1}}}{{{x_3}}}\left( {\frac{{ - {v_b} + {R_1}{x_1}}}{{{L_1}}} + \mathop {{i_{{\rm{bf}} - {\rm{ref}}}}}\limits^ \wedge } \right) $$ (6) $$ {\mu _{23{\rm{eq}}}} = \frac{{{L_2}}}{{{x_3}}}\left( {\frac{{{v_{{\rm{uc}}}} - {R_2}{x_2}}}{{{L_2}}} - \mathop {{i_{{\rm{uc}} - {\rm{ref}}}}}\limits^ \wedge } \right) $$ (7) 式中,${v_b} $为蓄电池等效电压;${L_1} $和${L_2} $为高频电感;$ {x_3}$为${v_{{\rm{dc}}}} $的平均值;$ {R_1} $为电感${L_1} $的等效串联电阻;$ {R_2} $为$ {L_2} $的等效串联电阻;$ \mathop {{i_{{\rm{bf}} - {\rm{ref}}}}}\limits^ \wedge $为$ {i_{{\rm{bf}} - {\rm{ref}}}} $平均值;$ \mathop {{i_{{\rm{uc}} - {\rm{ref}}}}}\limits^ \wedge $为$ {i_{{\rm{uc}} - {\rm{ref}}}} $的平均值。式(6)和式(7)可以分解成一般控制结构:
$${\mu _1} = {\mu _{1{\rm{eq}}}} + \frac{{{L_1}}}{{{x_3}}}\left( {{{\mathop \mu \limits^ \wedge }_{1N}} + {c_1}{\varepsilon _3}} \right) $$ (8) $$ {\mu _{23}} = {\mu _{23{\rm{eq}}}} - \frac{{{L_2}}}{{{x_3}}}{{\widehat \mu _{23N}}} $$ (9) 式中,$ {\mu _1} $和$ {\mu _{23}} $为占空比;即$ {u_1}$和$ {u_{23}} $的平均值;${c_1} > 0 $为设计参数;$ {\widehat \mu _{1N}}$和${\widehat \mu _{23N}} $作为附加输入信号,代表着一些干扰信号;$ {\varepsilon _3} = {x_3} - {x_{3d}} $,定义为$ {x_3} $与其设计值$ {x_{3d}} $之间的误差;$ {c_1}{\varepsilon _3} $为控制规则中的阻尼项,其作用是调整输出响应[12]。
2. 控制系统稳定性分析
滑模变结构控制策略的控制目标是使系统状态满足$ S = 0 $,为此必须确保在任何初始条件下,系统都能到达状态$ S = \dot S = 0 $,且保持$ S = 0$。此外,控制规则的选取必须在状态向量$({s_1}, {s_2}, {\varepsilon _3}) $下系统达到稳定。可建立二次李亚普洛夫函数:
$$ V = \frac{1}{2}{\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}} + \frac{1}{2}\varepsilon _3^2 $$ (10) 其导数为:
$$ \mathop V\limits^ \bullet = {s_1}{{\widehat \mu _{1N}}} + {s_2}{{\widehat \mu _{23N}}} + {\varepsilon _3}({c_1}{s_1} + {\dot \varepsilon _3}) $$ (11) 其中,有:
$$ {{\widehat \mu _{1N}}} = - {\alpha _1}{\mathop{\rm sgn}} ({s_1}) $$ (12) $$ {{\widehat \mu _{23N}}} = - {\alpha _2}{\mathop{\rm sgn}} ({s_2}) $$ (13) $$ {\dot \varepsilon _3} = - {\alpha _3}{\mathop{\rm sgn}} ({\varepsilon _3}) - {c_1}{s_1} $$ (14) 式中,$ {\alpha _1} > 0 $,$ {\alpha _2} > 0$,${\alpha _3} > 0 $均为设计参数。
式(11)可改写为:
$$ \mathop V\limits^ \bullet = - {\alpha _1}\left| {{s_1}} \right| - {\alpha _2}\left| {{s_2}} \right| - {\alpha _3}\left| {{\varepsilon _3}} \right| $$ (15) 式中,$ \mathop V\limits^ \bullet \le 0 $,根据李亚普洛夫第二法(直接法)可知,含状态向量$ ({s_1}, {s_2}, {\varepsilon _3}) $的闭环系统全局渐近稳定。
结合式(6)~式(9)以及式(12)~式(14),得到如下控制规则:
$$ {\mu _1} = 1 + \frac{{{L_1}}}{{{x_3}}}\left( {\frac{{ - {v_b} + {R_1}{x_1}}}{{{L_1}}} - {\alpha _1}{\mathop{\rm sgn}} ({s_1}) + {c_1}{\varepsilon _3} + \mathop {{i_{{\rm{bf}} - {\rm{ref}}}}}\limits^ \wedge } \right) $$ (16) $$ {\mu _{23}} = \frac{{{L_2}}}{{{x_3}}}\left( {\frac{{{v_{{\rm{uc}}}} - {R_2}{x_2}}}{{{L_2}}} + {\alpha _2}{\mathop{\rm sgn}} ({s_2}) - \mathop {{i_{{\rm{uc}} - {\rm{ref}}}}}\limits^ \wedge } \right) $$ (17) ${x_3} $的设计值$ {x_{3d}} $定义为:
$$ \mathop {{x_{3d}}}\limits^ \wedge = \frac{1}{{{C_{{\rm{dc}}}}}}[(1 - {\mu _1}){x_1} + {\mu _{23}}{x_2} - {i_o}] - {\alpha _3}{\mathop{\rm sgn}} ({\varepsilon _3}) - {c_1}{s_1} $$ (18) $$ {x_{3d}} = \frac{1}{s}\left\{ {\frac{1}{{{C_{{\rm{dc}}}}}}[(1 - {\mu _1}){x_1} + {\mu _{23}}{x_2} - {i_o}] - {\alpha _3}{\mathop{\rm sgn}} ({\varepsilon _3}) - {c_1}{s_1}} \right\} $$ (19) 式中,$ {C_{{\rm{dc}}}} $为直流母线电压的输出滤波电容;$ {i_o} $为复合电源输出电流;s为拉普拉斯算子。
3. 仿真研究
3.1 仿真平台
为验证本文提出的基于滑模变结构和李雅普诺夫的复合电源功率分配稳定控制策略的理论可行性,在ADVISOR仿真环境下进行仿真研究[13]。本文中的研究对象为小型轻混合度混合动力电动汽车,仿真平台的具体参数如表 1所示。关于设计参数$ {\alpha _1} $、$ {\alpha _2} $和$ {\alpha _3} $,根据其数学表现形式和实际作用可以看出,3个设计参数均属于经验值,具体参数选择方法为试凑法,具体参数值设计为:$ {\alpha _1} = {10^4} $,$ {\alpha _2} = {10^3} $,$ {\alpha _3} = {10^4} $,$ {c_1} = 2 $。
表 1 仿真平台参数参数 整车 蓄电池 超级电容器 满载质量/kg 1 919 — — 迎风面积/m2 2.0 — — 空气阻力系数 0.336 — — 驱动电机功率/kW 58 — — 单体额定电压/V — 12 2.7 单体额定容量/Ah — 30 500 数目(串联) — 20 110 Boost变换器和Buck-Boost变换器的具体仿真参数如表 2所示。
表 2 功率变换器仿真参数名称 数值 L1、L2/mH 5 R1、R2/mΩ 20 Cdc/mF 1.67 Cb/mF 1.67 Cuc/F 500 Ruc/Ω 0.5 开关频率fs /kHz 15 3.2 仿真结果与分析
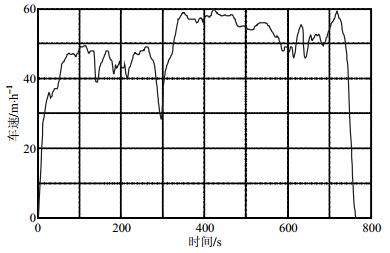
选择CYC-HWFET工况作为测试工况,如图 2所示,该工况可测试混合动力电动汽车的各项性能,代表性较强。
图 3为复合电源的仿真结果,从控制目标实现和复合电源功能实现两个角度对仿真结果进行分析。
1) 控制目标实现角度
图 3a所示为直流母线电压,直流母线电压在336 V上下波动,电压波动范围在10 V左右,稳压精度小于3%,第一个控制目标已实现。图 3b所示为超级电容器电流参考值和实际值,图 3c所示为两者之间的相对误差。超级电容器实际电流精确跟踪其参考值,误差精度控制在3%以内,第二个控制目标已实现。
2) 复合电源功能实现角度
图 3d和图 3e所示为蓄电池和超级电容器的电压和电流波形,蓄电池的电压特性较硬,电压波形基本恒定,变化波动范围较小。超级电容器电压特性较软,电压波动范围较大;蓄电池的电流相对于超级电容器,其变化幅度较小,超级电容器最大限度地发挥了其大电流瞬时充放电的优势,有效及时地对蓄电池进行了功率补偿,功率补偿效果较好。复合电源中蓄电池和超级电容器优势互补的功能得以实现。
4. 实验研究
4.1 实验平台
搭建的小功率复合电源实验平台如图 4所示,实验平台由3个部分组成,第一部分为复合电源系统,包括蓄电池、超级电容器和功率变换器;第二部分为负载,包括直流他励电机、涡流制动器和冷却水箱;第三部分为测试平台,包括电压电流传感器和PC机。具体实验参数如表 3所示。
表 3 复合电源实验参数参数 蓄电池 超级电容器 DC/DC变换器 单体额定电压/V 6 3 — 单体额定容量/Ah 20 650 — 数目(串联) 4 12 — 开关频率/kHz — — 20 电感量/μH — — 100 4.2 实验结果与分析
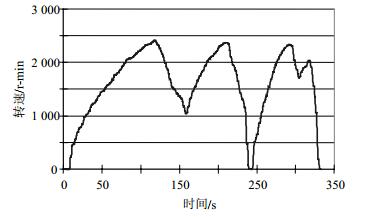
实验工况如图 5所示,该工况中包含加速、减速和制动等运行状态,与仿真CYC-HWFET工况相对应。
实验结果如图 6所示,同样从控制目标实现和复合电源功能实现两个角度对实验结果进行剖析。
1) 控制目标实现角度
图 6a所示为直流母线电压,电压波动范围为1.2 V,稳压精度小于2.5%。图 6b为超级电容器电流参考值和实际值,可以看出电容电流的实际值时刻跟踪其参考值,图 6c给出了实际值和参考值之间的相对误差,误差在5%以内,跟踪性能较好。两个控制目标均已实现。
2) 复合电源功能实现角度
图 6d所示为电池和电容的电压曲线,电压特性较硬的蓄电池,其电压基本为一条水平线。电压特性较软的超级电容器,实验过程中的电压波动较为明显。图 6e所示为电池和电容的电流,以电机转速为切入点进行分析。电机启动时刻,负载需求功率较小,不存在峰值功率,此时由蓄电池提供功率。当电机转速提高,负载需求功率增大,同时实验工况中出现了明显的加减速,超级电容器逐步对电池进行功率补偿,呈现出电容大电流充放电的情况。至此,复合电源的功能再次在实验中得以实现。
从控制目标和复合电源功能实现两个角度不难发现,仿真结果和实验结果高度一致。
5. 结束语
本文针对混合动力电动汽车复合电源功率分配控制问题,提出了一种基于滑模变结构和李雅普诺夫的稳定控制策略。经过仿真和实验验证后,结论如下:
1) 本文的控制策略能实现稳定直流母线电压、精确跟踪超级电容器电流参考值两个控制目标;
2) 闭环控制系统能实现全局渐近稳定;
3) 本文的功率分配控制策略其意义在于:蓄电池和超级电容器各自能发挥所长,优势互补,在充分保证汽车能量和功率双重动力需求的同时,提高了汽车的续航能力,大大降低了储能系统的长期成本。
-
表 1 仿真平台参数
参数 整车 蓄电池 超级电容器 满载质量/kg 1 919 — — 迎风面积/m2 2.0 — — 空气阻力系数 0.336 — — 驱动电机功率/kW 58 — — 单体额定电压/V — 12 2.7 单体额定容量/Ah — 30 500 数目(串联) — 20 110 表 2 功率变换器仿真参数
名称 数值 L1、L2/mH 5 R1、R2/mΩ 20 Cdc/mF 1.67 Cb/mF 1.67 Cuc/F 500 Ruc/Ω 0.5 开关频率fs /kHz 15 表 3 复合电源实验参数
参数 蓄电池 超级电容器 DC/DC变换器 单体额定电压/V 6 3 — 单体额定容量/Ah 20 650 — 数目(串联) 4 12 — 开关频率/kHz — — 20 电感量/μH — — 100 -
[1] FADIL H El, GIRI F. Sliding mode control of fuel cell and supercapacitor hybrid energy storage system[C]//8th Power Plant and Power System Control Symposium Proceedings. France: IFAC Proceedings Volumes, 2012, 45(21): 669-674.
[2] 王琪, 孙玉坤.一种混合动力汽车复合电源能量管理系统控制策略与优化设计方法研究[J].中国电机工程学报, 2014, 34(s):195-203. http://www.cqvip.com/QK/90021X/2014S1/90716867504849528349485057.html WANG Qi, SUN Yu-kun. Research on the control strategy and optimization of energy management system of hybrid energy storage in a hybrid electric vehicle[J]. Proceedings of CHEE, 2014, 34(s):195-203. http://www.cqvip.com/QK/90021X/2014S1/90716867504849528349485057.html
[3] 沈阳武, 彭晓涛, 杨军, 等.超级电容器储能系统的功率实时控制[J].电力自动化设备, 2011, 31(11):28-32. DOI: 10.3969/j.issn.1006-6047.2011.11.006 SHEN Yang-wu, PENG Xiao-tao, YANG Jun, et al. Real-time power control of ultracapacitor energy storage system[J]. Electric Power Automation Equipment, 2011, 31(11):28-32. DOI: 10.3969/j.issn.1006-6047.2011.11.006
[4] KHALIGH A, LI Zhi-hao. Battery, ultracapacitor, fuel cell, and hybrid energy storage systems for electric, hybrid electric, fuel cell, and plug-in hybrid electric vehicles:state of the art[J]. IEEE Transactions on Vehicular Technology, 2010, 58(6):2806-2814. http://ieeexplore.ieee.org/document/5446335/
[5] ROTENBERG D, VAHIDI A, KOLMANOVSKY I. Ultracapacitor assisted powertrains:Modeling, control, sizing, and the impact on fuel economy[J]. IEEE Transaction on Control System Technology, 2011, 19(3):576-589. DOI: 10.1109/TCST.2010.2048431
[6] SAMOSIR A S, YATIM A H M. Implementation of dynamic evolution control of bidirectional DC-DC converter for interfacing ultracapacitor energy storage to fuel-cell system[J]. IEEE Transaction on Industrial Electronics, 2010, 57(10):3468-3473. DOI: 10.1109/TIE.2009.2039458
[7] CHEN B C, WU Y Y, LIN C C. Adaptive power split control for a hybrid electric scooter[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4):1430-1437. DOI: 10.1109/TVT.2011.2132155
[8] MICHALCZUK M, UFNALSKI B, GRZESIAK L. Fuzzy logic control of a hybrid battery-ultracapacitor energy storage for an urban electric vehicle[C]//20138th International Conference and Exhibition on Ecological Vehicles and Renewable Energies. Monte Carlo: IEEE, 2013: 1-7.
[9] 张京明, 任殿波, 崔淑梅, 等.并联混合动力汽车复合电源控制策略的研究[J].高技术通讯, 2010, 20(3):298-302. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gjstx98201003013 ZHANG Jing-ming, RENG Dian-bo, CUI Shu-mei, et al. The research on a strategy for control of composite power in parallel hybrid electric vehicles[J]. Chinese High Technology Letters, 2010, 20(3):298-302. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gjstx98201003013
[10] 王琪, 孙玉坤, 罗印升.混合动力电动汽车的复合电源功率分配控制策略[J].电工技术学报, 2017, 32(18):143-151. http://mall.cnki.net/magazine/Article/DYJS201205013.htm WANG Qi, SUN Yu-kun, LUO Yin-sheng. A power distribution control strategy of hybrid energy storage system in hybrid electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(18):143-151. http://mall.cnki.net/magazine/Article/DYJS201205013.htm
[11] 王琪, 孙玉坤, 陈坤华, 等.半主动式结构的蓄电池-超级电容器复合电源[J].江苏大学学报(自然科学版), 2014, 35(4):428-433. http://www.cnki.com.cn/Article/CJFDTotal-DGJZ201422016.htm WANG Qi, SUN Yu-kun, CHEN Kun-hua, et al. A semi-active battery-ultracapacitor hybrid energy source[J]. Journal of Jiangsu University(Natural Science Edition), 2014, 35(4):428-433. http://www.cnki.com.cn/Article/CJFDTotal-DGJZ201422016.htm
[12] eL FADIL H, GIRT F, OUADI H. Accounting for coils magnetic saturation in controlling DC-DC power converters[C]//IEEE International Conference on Control Applications(CCA). Munich: IEEE, 2006: 3163-3168.
[13] eL FADIL H, GIRI F, GUERRERO J M. Lyapunov based control of hybrid energy storage system in electric vehicles[C]//Proceedings of the American Control Conference (ACC). Montreal: IEEE, 2012: 5005-5010.
[14] 王琪, 孙玉坤, 倪福银, 等.一种混合动力电动汽车电池荷电状态预测的新方法[J].电工技术学报, 2016, 31(9):189-196. DOI: 10.3969/j.issn.1000-6753.2016.09.024 WANG Qi, SUN Yu-kun, NI Fu-yin, et al. A new method of battery state of charge prediction in the hybrid electric vehicle[J]. Transactions of China Electrotechnical Society, 2016, 31(9):189-196. DOI: 10.3969/j.issn.1000-6753.2016.09.024
-
期刊类型引用(3)
1. 齐冠然,杨淑贞,李民,卢金生,李洪涛. 曳引电梯蓄能器储能液压节能系统及电容能耗研究. 机床与液压. 2023(03): 146-150 .  百度学术
百度学术
2. 潘龙,王合闯,楚明月,林茂盛,杜立江,张中宽. 基于DSP的正弦波逆变电源瞬时值反馈优化控制方法. 电源学报. 2023(05): 51-57 .  百度学术
百度学术
3. 张细政,卢张宇,谭崇茁,郑亮. 基于指数趋近律的车载复合储能系统全局滑模控制. 控制与决策. 2021(04): 885-892 .  百度学术
百度学术
其他类型引用(5)

 ISSN
ISSN 



 下载:
下载: