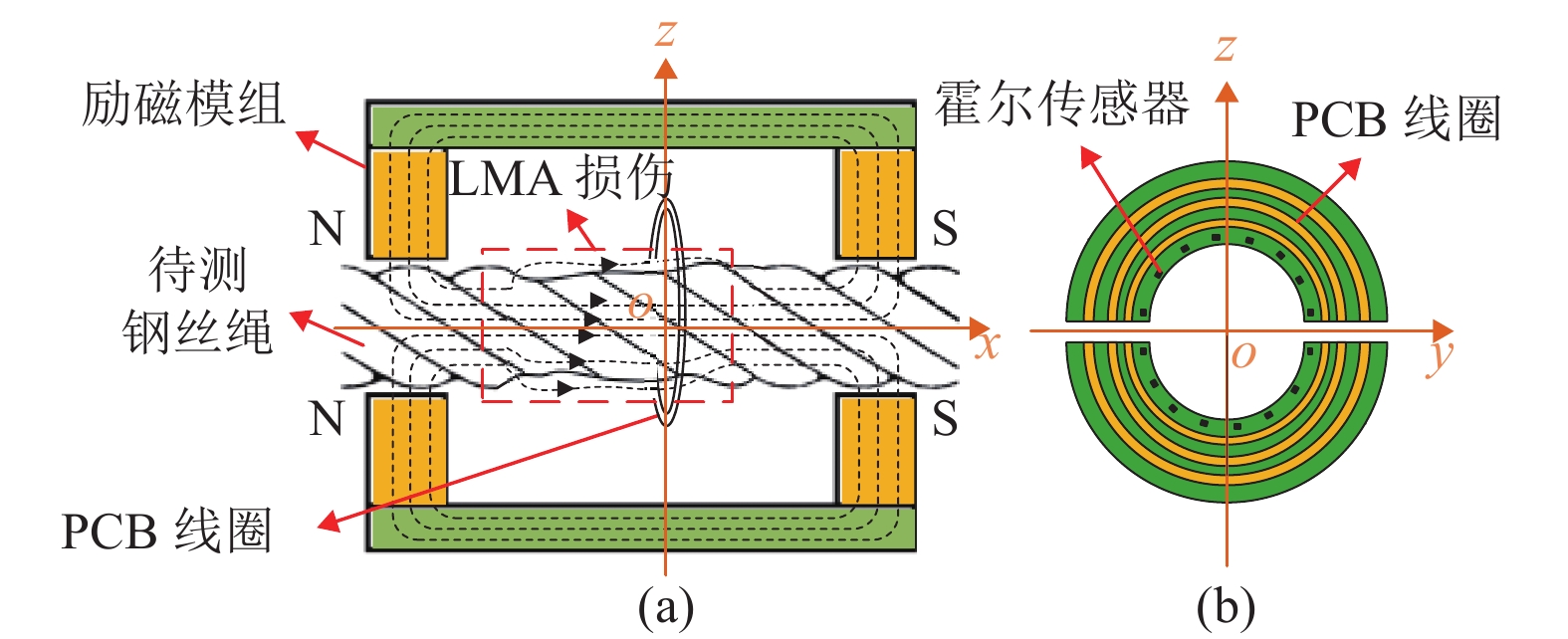
-
钢丝绳作为一种柔性部件,具有承载能力强、柔韧性突出、工作稳定性好等优点[1-3]。在使用过程中,钢丝绳不可避免地发生磨损、断丝和腐蚀等损伤[4-6],导致其金属横截面积不断减小,严重影响弹性性能、承载能力等工作特性。国内外针对钢丝绳金属横截面积损失(Loss of Metallic Area, LMA)制定了相关检测和报废标准[7, 8],但目前LMA检测方法误差大、检测设备安装复杂成为制约钢丝绳无损检测的瓶颈。因此,快速准确地检测钢丝绳LMA,对相关装备运行安全及设备可靠性具有重要意义[9]。
目前,针对LMA的漏磁检测方法主要分为磁通检测法[10]、磁桥检测法[5]及漏磁反演法[11]。其中磁通检测法通过感应线圈检测磁通变化能够直观反映LMA损失量,避免了磁桥分布对检测信号的影响及理论模型中存在的误差。近年来国内外学者针对线圈结构及磁路设计进行了大量的研究,提出双排差动线圈[12]、周向分布线圈[13]及聚磁检测线圈[14]等改善设计,优化了LMA检测效果。此类传统线圈通常由导线手工绕制,灵活性较高,但绕制过程繁琐、参数难以修改,同时受到待测件直径、形状及传感器设计影响较大,难以标准化。相较于传统线圈,近年来由于制作工艺提升,PCB线圈因其紧凑电路结构及生产过程中的一致性得到工业广泛应用。在钢丝绳无损检测场景中,由于工况中钢丝绳的连续性使得传统线圈无法预制和预安装,因此采用PCB线圈个性化设计为此提供了一种新的解决方案。
本文基于钢丝绳电磁检测原理,提出一种基于印刷电路板(Printed Circuit Board, PCB)线圈分体结构的传感器设计方法,通过仿真数据分析线圈设计参数对检测效果的影响。同时,针对线圈LMA检测受损伤宽度影响较大的问题,提出补偿方案。最后,结合仿真及实验数据,拟合损伤程度与磁通变化量间的线性关系,验证PCB线圈的检测与量化能力。
-
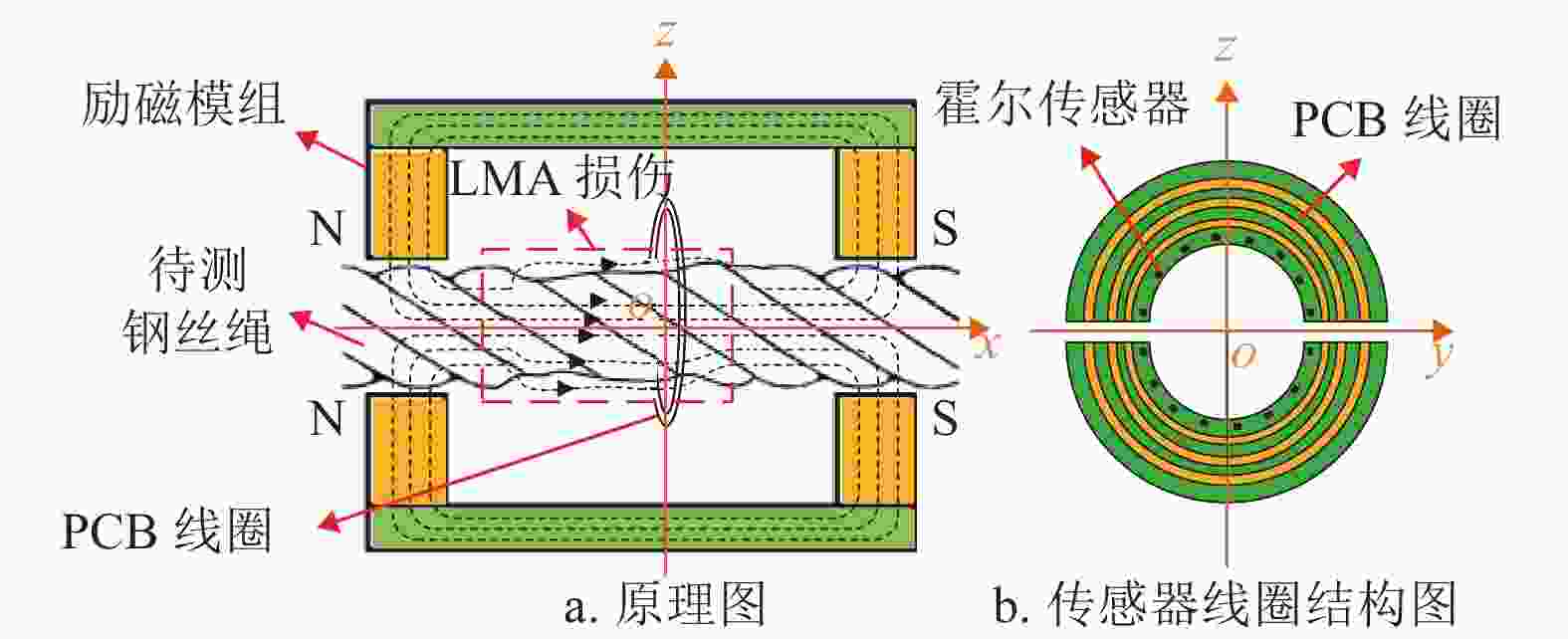
钢丝绳主磁通检测原理如图1(a)所示,当钢丝绳受到足够磁场激励时,会被饱和磁化,与磁场源形成完整磁路。当钢丝绳产生LMA类损伤时,损伤处由相对磁导率较高的铁磁材料变为空气,由此产生的磁通量改变引起检测线圈感应电压发生变化[15]。
当钢丝绳未发生损伤时,线圈中的总磁通量可以表示为:
$$ \begin{split} &\quad \varPhi = {\varPhi _{{\text{wr}}}} + {\varPhi _{{\text{air}}}} \\ & = {B_{{\text{wr}}}}{S_{{\text{wr}}}} + {B_{{\text{air}}}}{S_{{\text{air}}}} \\ \end{split} $$ (1) 式中,
$ \varPhi $ 、$ {\varPhi _{{\text{wr}}}} $ 、$ {\varPhi _{{\text{air}}}} $ 分别是未发生损伤时线圈中的总磁通量、钢丝绳内部磁通量、钢丝绳表面与线圈中气隙的磁通量;$ {B_{{\text{wr}}}} $ 、$ {B_{{\text{air}}}} $ 分别是钢丝绳内部及外部气隙中的磁感应强度;$ {S_{{\text{wr}}}} $ 、$ {S_{{\text{air}}}} $ 是未发生损伤时钢丝绳及外部气隙的横截面积。当钢丝绳产生LMA类损伤时,钢丝绳减少的横截面积等于空气增加的横截面积,此时线圈中的总磁通量为:
$$ {\varPhi ^{'}} = {B_{{\text{wr}}}}({S_{{\text{wr}}}} - \Delta S) + {B_{{\text{air}}}}({S_{{\text{air}}}} + \Delta S) $$ (2) 式中,
$ {\varPhi ^{'}} $ 是损伤后线圈中的总磁通量,$ \Delta S $ 是钢丝绳损失的横截面积。因此,线圈中磁通量变化量为:
$$ \varDelta \varPhi = \varPhi - \varPhi ' = \left( {{B_{{\text{wr}}}} - {B_{{\text{air}}}}} \right)\varDelta S $$ (3) 由式(3)可见,钢丝绳金属横截面积的变化与线圈中磁通量变化量成线性关系。随着截面积损失增大,线圈中的磁通量变化量增加,其感应电压可表示为[16]:
$$ v = - N\frac{{\Delta \varPhi }}{{\Delta t}} $$ (4) 式中,N为线圈匝数,
$ \Delta \varPhi $ 为线圈中磁通量变化量。 -
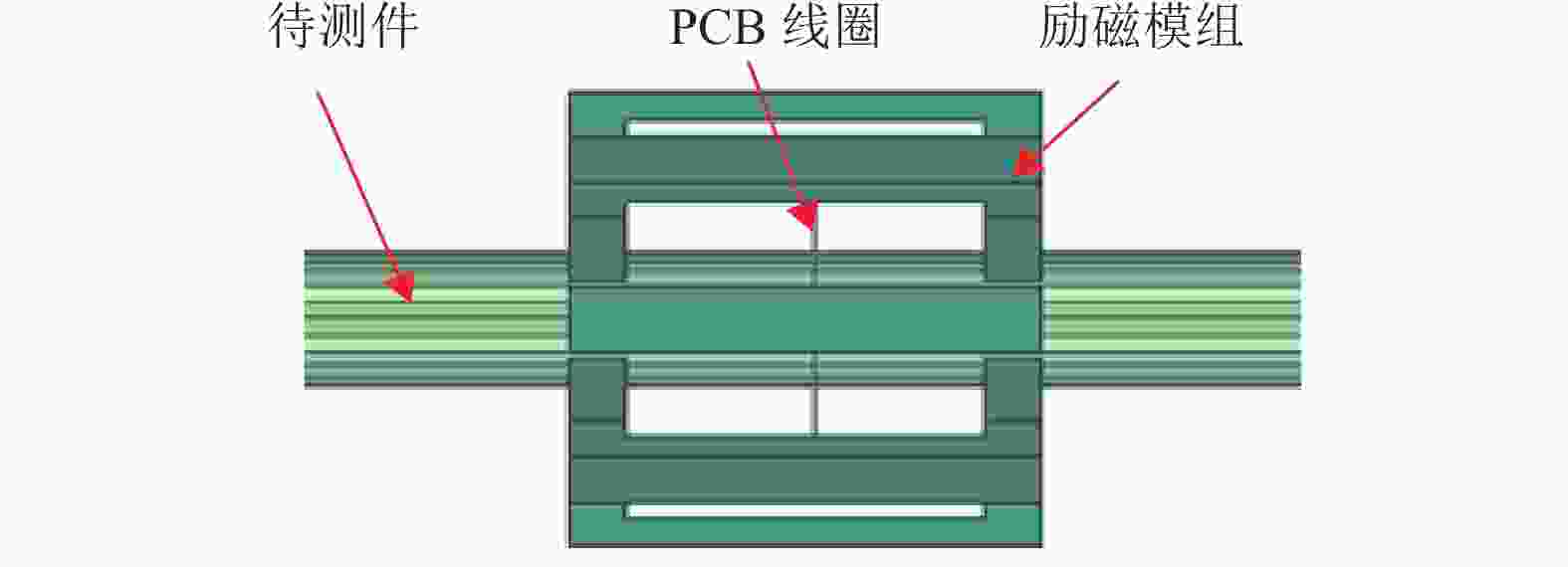
主磁通检测传感器线圈结构如图1(b)所示,本文利用仿真规划PCB线圈结构参数、分布参数及引线位置,并通过柔性电路板(Flexible Printed Circuit, FPC)连接线插头将两部分线圈结构组合,进而检测完整主磁通变化。
表1为PCB线圈的6种设计参数,其中匝数与提离值可以根据理论计算获得,其余四个参数主要受加工工艺和传感器空间等多因素影响,难以直接表达。因此为分析线圈结构对检测效果的影响,本文利用ANSYS Maxwell仿真软件对线圈的设计参数进行分析。由于钢丝绳的复杂螺旋结构特征,其模型网格数量十分庞大,结果往往超出ANSYS的计算范围。同时,饱和磁化时相同直径钢丝绳与钢管的磁通量差距较小[5],为提高仿真效率,本文使用等效钢管模型作为简化的钢丝绳模型。如图2所示,通过8组周向分布的永磁体模块对等效模型饱和磁化,模型具有1%损失率的LMA损伤,分析PCB线圈检测的损伤信号,从而指导PCB线圈结构设计与优化。
表 1 PCB线圈设计参数
线圈参数 含义 单位 m 线圈层数 层 z 线圈匝数 匝 d 线距 mm w 线宽 mm e 印刷铜厚 mm h 线圈距钢丝绳表面的提离距离 mm 由于表1中的PCB线圈设计参数为独立变量,不相互影响,因此,采用变量控制法对线圈的最终设计参数进行研究。其中,为研究PCB线圈的最优匝数及分布,考虑PCB受传感器的内部空间限制,仿真验证了相同损伤和运行速度下不同匝数线圈的感应电压。如图3所示,感应电压与线圈匝数成正比,与理论相符,因此为改善检测效果,应在允许范围内增加线圈匝数。当匝数固定时,平面线圈层数即PCB层数对检测效果影响有限,但考虑制造工艺、加工成本及电路复杂程度等因素,单层PCB线圈更适用于实际LMA检测。
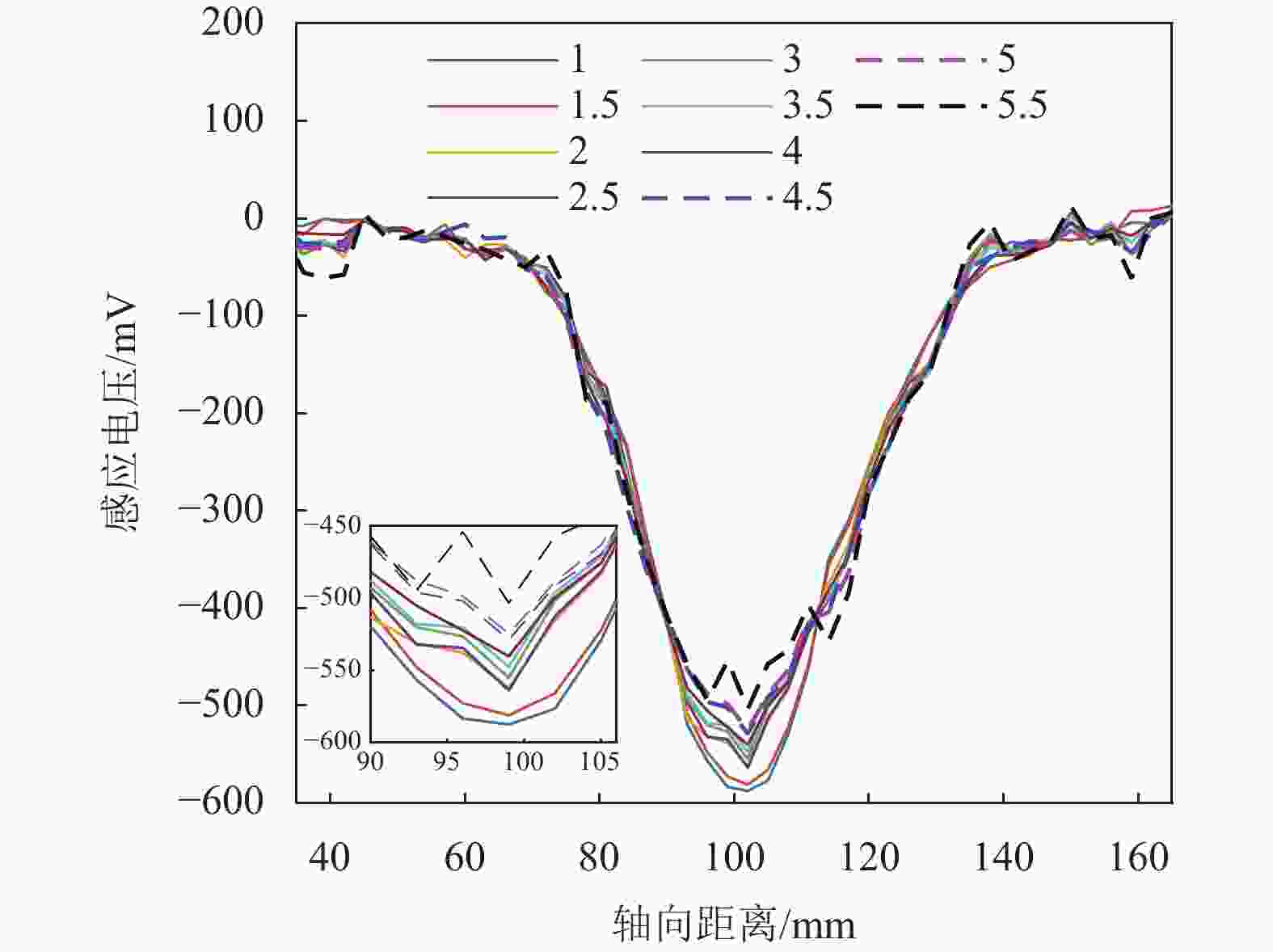
除此之外,本文仿真分析了40匝单层线圈下,不同线距d、线宽w、提离值h以及印刷铜厚e对线圈中的感应电压的影响规律。如图5~图8所示,线距、线宽及提离值的增大会导致感应电压降低,其中每增加0.01 mm线距,峰值减小约0.4%,每增加0.01 mm线宽峰值减小约0.38%,而提离值每增加0.5 mm,电压峰值减小约1.1%。印刷铜厚对于检测效果的影响微弱,可忽略不计。
基于仿真结果中各参数对检测电压的影响规律,本文结合实际PCB板制作工艺、性价比等多方面考虑,形成了最优设计参数选择方案如下:(1)根据传感器空间和实际限制确定PCB板加工中难以调整的线宽、线距及铜厚参数;(2)优先考虑匝数,接着考虑提离值,最后考虑层数。最终根据实际传感器设计和参数影响规律,设计参数为单层40匝线圈结构,其中线宽0.15 mm,线距0.176 mm,铜厚0.035 mm,提离值为5 mm。
-
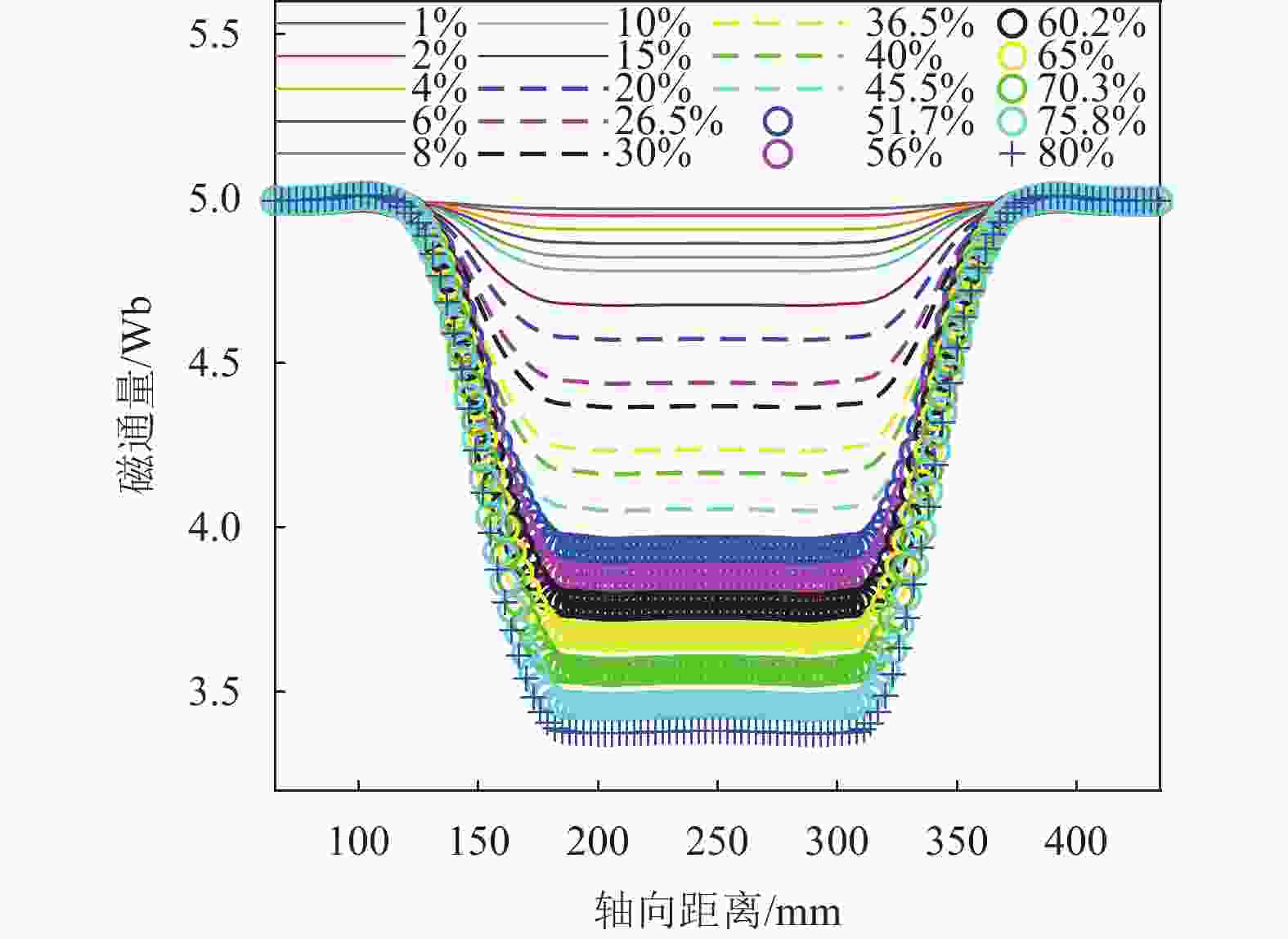
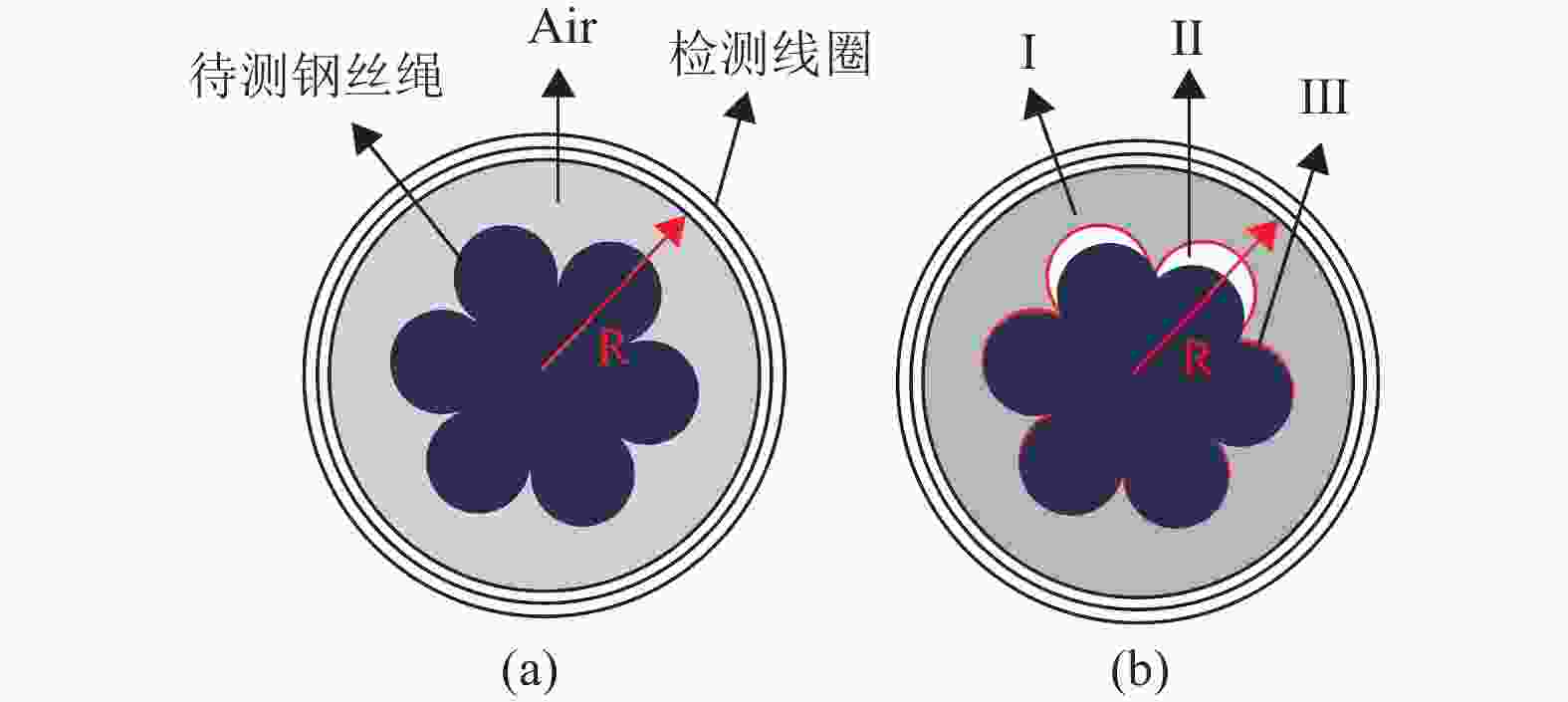
本文基于图2的仿真模型,通过设置长度L=190 mm的不同损失率的LMA损伤进行分析。图9展示了线圈内部磁通量随LMA的变化趋势,当损失率逐渐增大时,线圈内部磁通量逐渐减小。这是由于当钢丝绳发生磨损时,气隙区域由原有的区域Air增大为区域I和II。根据式(3)和式(4),检测线圈电压信号取决于线圈内部磁通变化量,当钢丝绳产生LMA损伤时,PCB线圈中的磁通量可进一步表示为:
$$ \varPhi ' = {B_{{\text{wr}}'}}(S - \varDelta S) + {B_{{\text{air2}}}}\varDelta S + {B_{{\text{air1}}}}{S_{{\text{air}}}} $$ (5) 式中,
$ {B_{{\text{wr}}'}} $ 是发生磨损后钢丝绳内部的磁感应强度;${B_{{\text{air1}}}}$ 是空气区域I的磁感应强度,${B_{{\text{air2}}}}$ 是空气区域II中的磁感应强度;$\Delta S$ 为区域I的LMA大小。此时,PCB线圈中的磁通量变化量
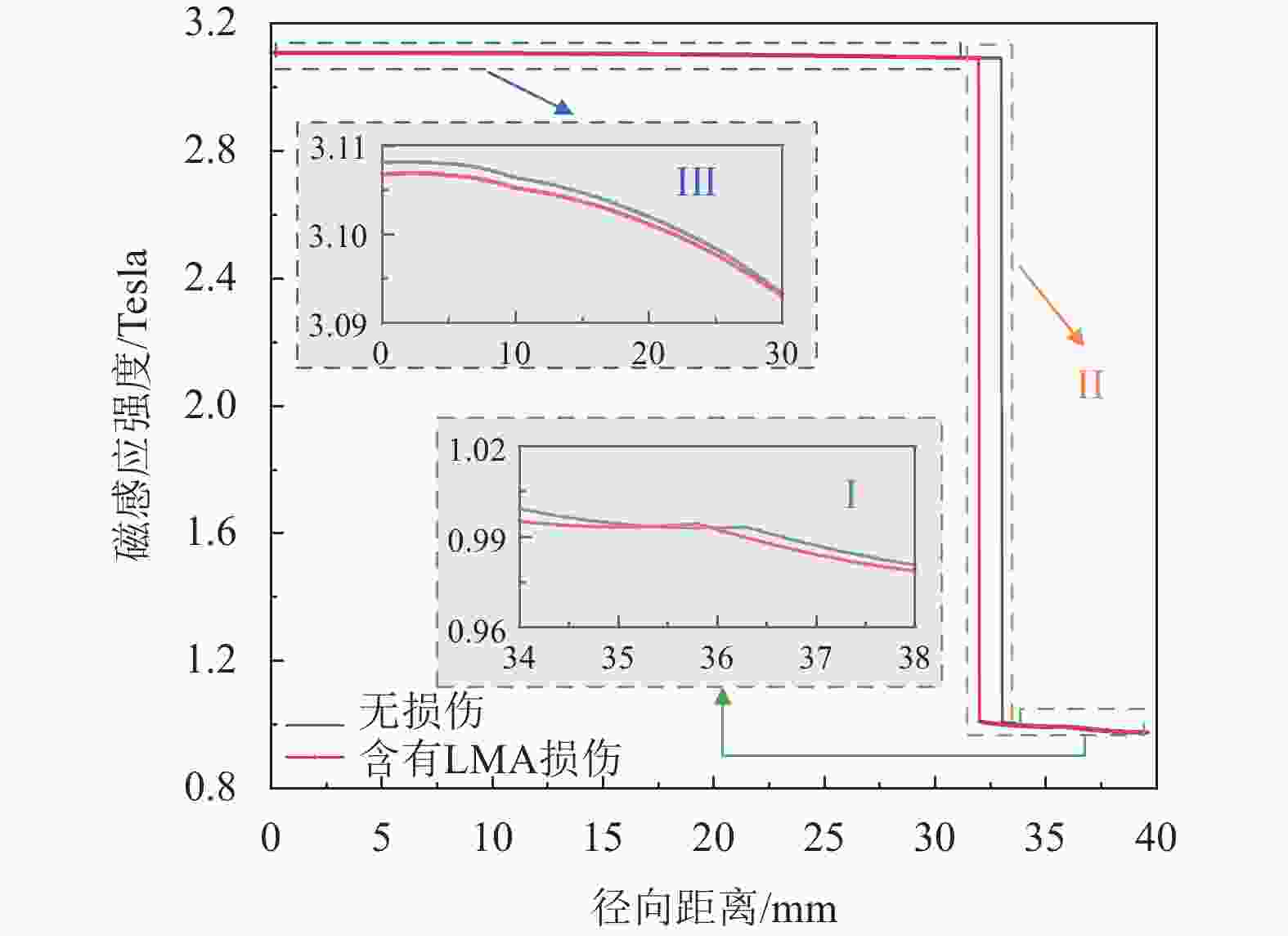
$\Delta \varPhi '$ 为:$$ \begin{split} & \Delta \varPhi ' = ({B_{{\text{wr}}'}} - {B_{{\text{air2}}}})\Delta S - ({B_{{\text{wr}}}} - {B_{{\text{wr'}}}})S \\ &\qquad\qquad - ({B_{{\text{air}}}} - {B_{{\text{air1}}}}){S_{{\text{air}}}} \end{split} $$ (6) 通过仿真对如图10所示的线圈半径方向上的磁感应强度变化进行分析,结果如图11所示,在区域II处由于铁磁材料磨损为空气,因此区域II磨损前后磁感应强度差异较大。但同时由图11可知,钢丝绳内部的磁感应强度变化量与空气区域I中的磁感应强度变化量,即图中区域I与III变化量近似相等,式(6)可进一步表示为:
$$ \Delta \varPhi ' = ({B_{{\text{wr}}}} - {B_{{\text{air}}}})\Delta S - \Delta B(S + {S_{{\text{air}}}}) $$ (7) -
由式(7)可得,PCB线圈中的磁通量变化量
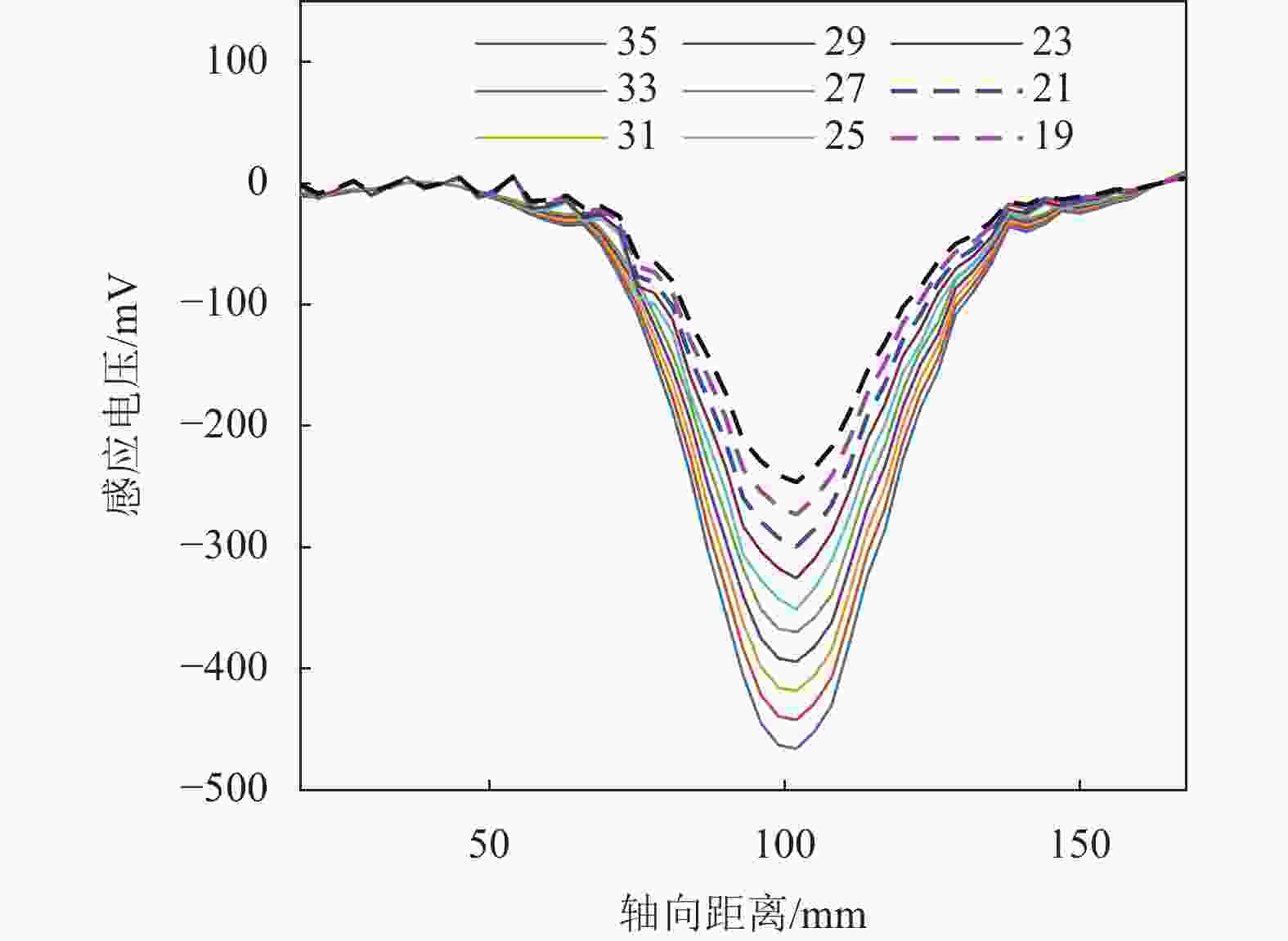
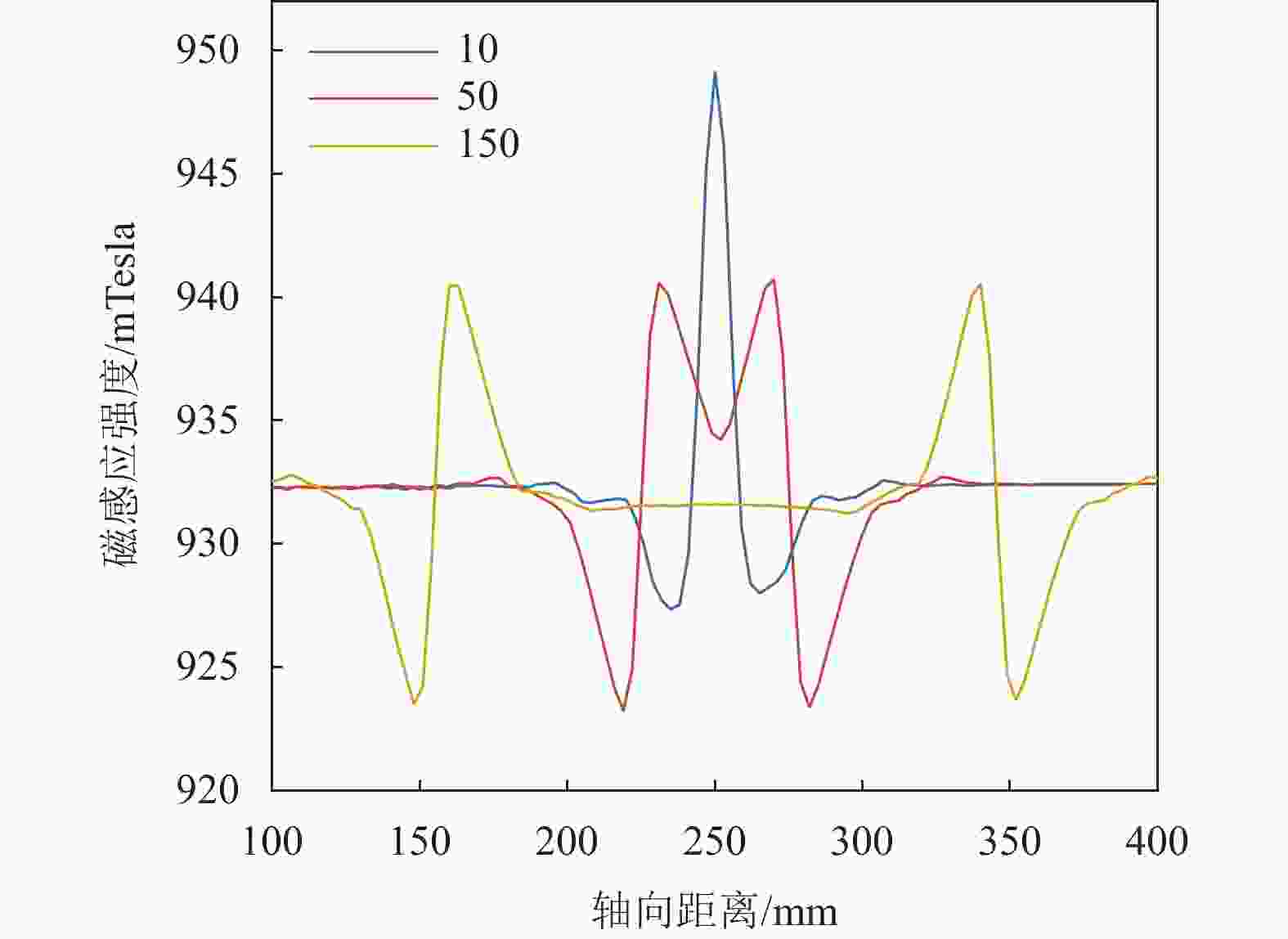
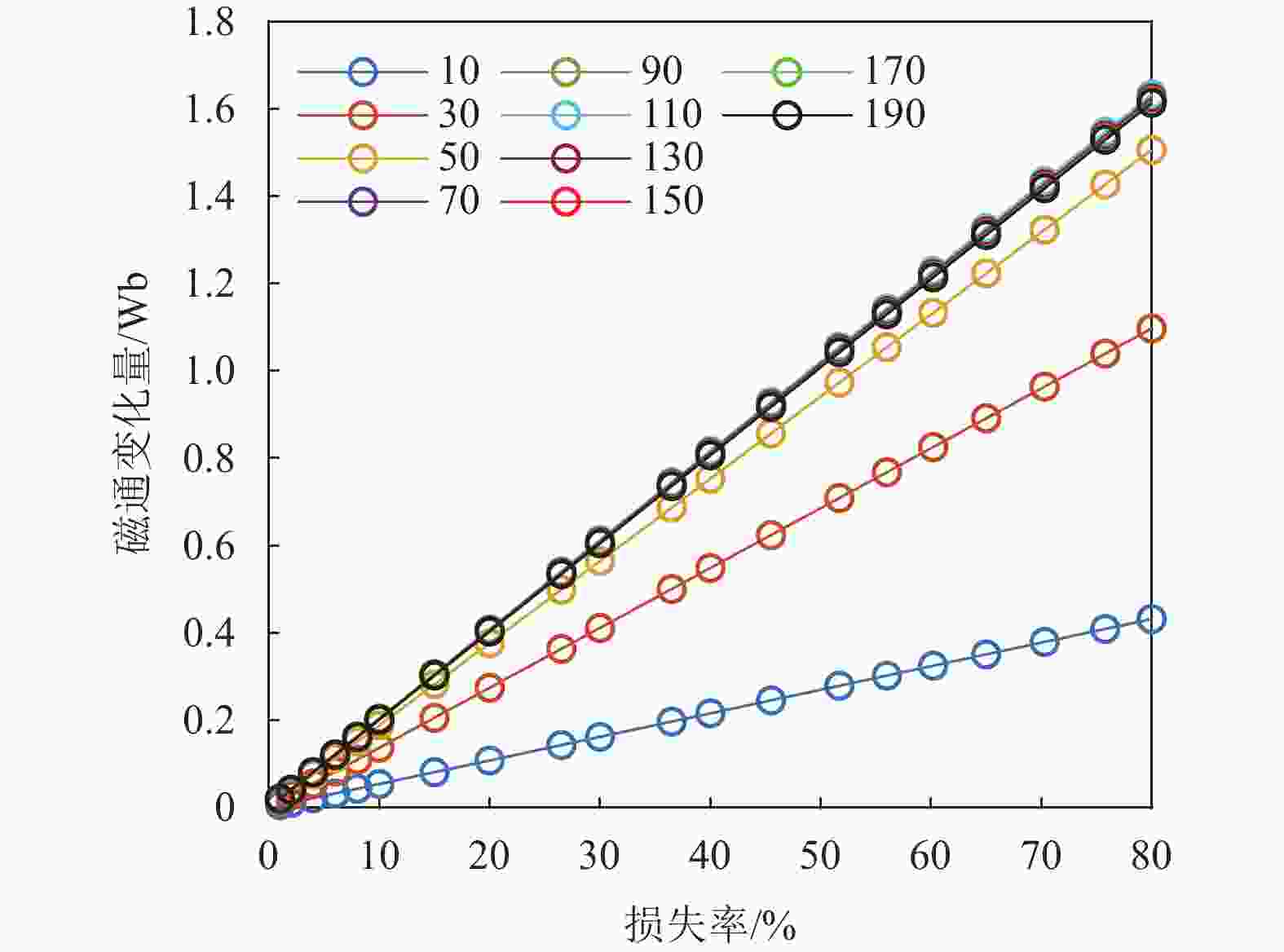
$ \Delta \varPhi ' $ 与钢丝绳横截面积损失成正比,与空气中的漏磁场变化量$ \Delta B $ 成反比。但当对相同LMA值、不同轴向宽度的损伤模型进行仿真分析时,空气中磁场分布存在显著差异。当传感器两端磁极间距为106 mm时,针对2 mm~160 mm的不同损伤宽度进行了分析,其中损伤宽度分别为10 mm、50 mm、150 mm的典型磁场强度分布形态如图12所示。当损伤宽度小于20 mm时,漏磁场呈现为类脉冲形态,随着损伤宽度增大漏磁场宽度逐渐增大。当损伤宽度大于20 mm时,漏磁场逐渐分离出两个波峰,并随着宽度增大波峰逐渐远离。当损伤宽度超过磁极间距时,漏磁场形态不再变化,但峰值依然受到影响。因此即使LMA值一定,损伤宽度依然会影响漏磁场分布,进而影响检测线圈内部磁通量变化,为后续的定量分析带来困难。仿真设计了不同损伤宽度模型,其磁通变化量与损失率之间的关系如图13所示。当损伤宽度一定时,损失率与磁通变化量呈正比关系。由图13可见,损伤宽度越小,磁通变化量随损失率变化的斜率越小。
为减弱损伤宽度对检测效果的影响,通过式(7)对测量结果进行补偿,补偿量为
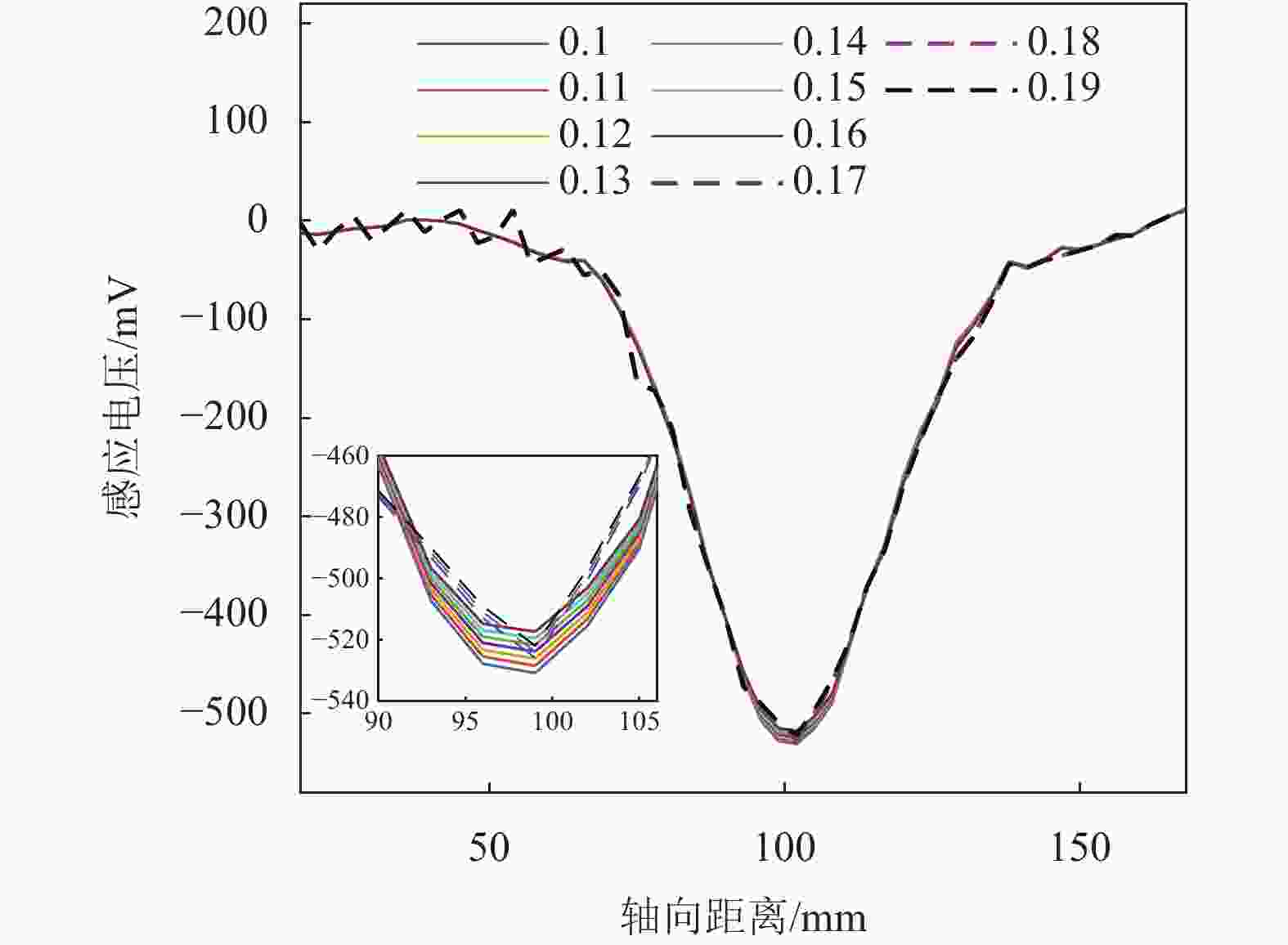
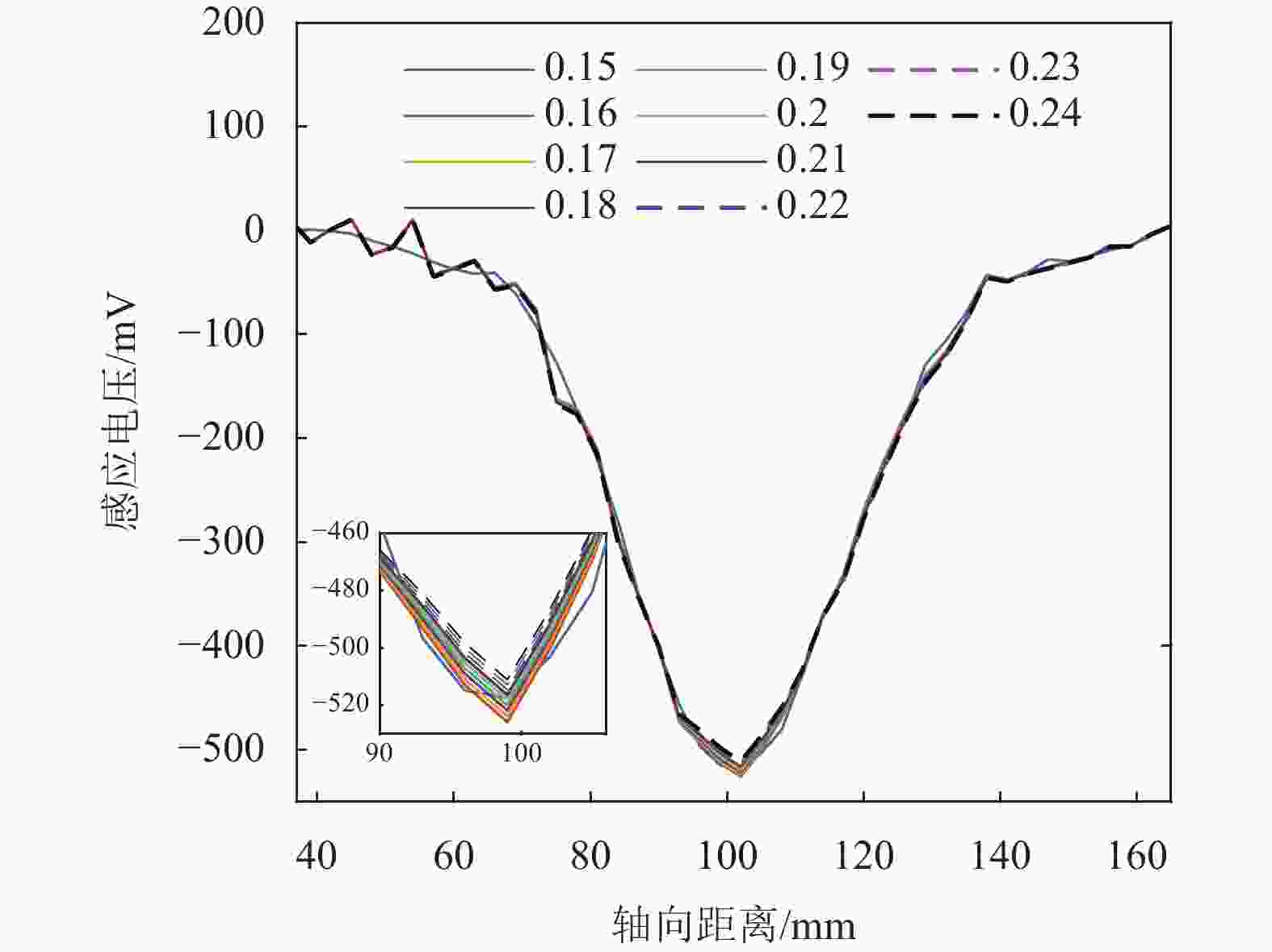
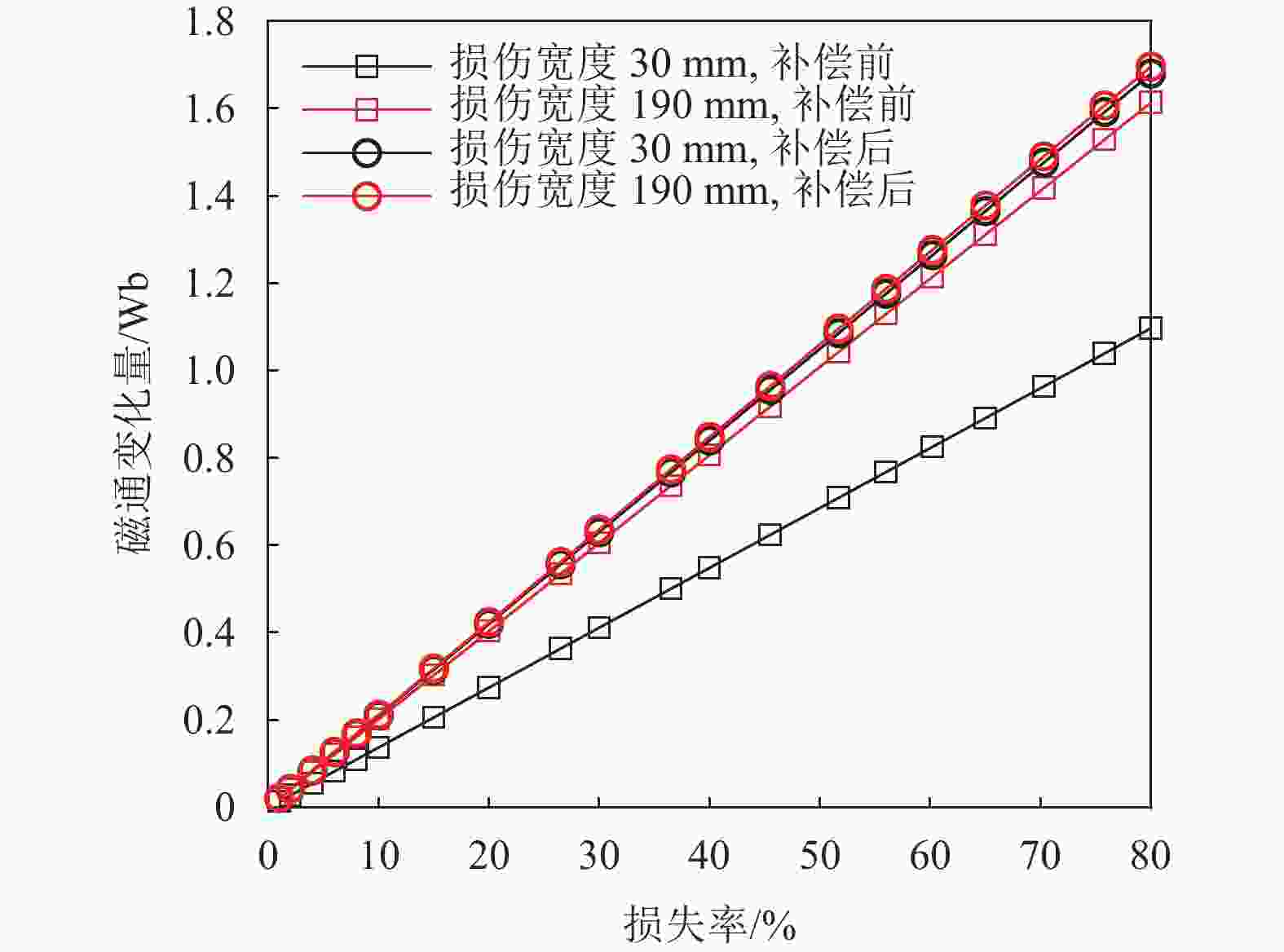
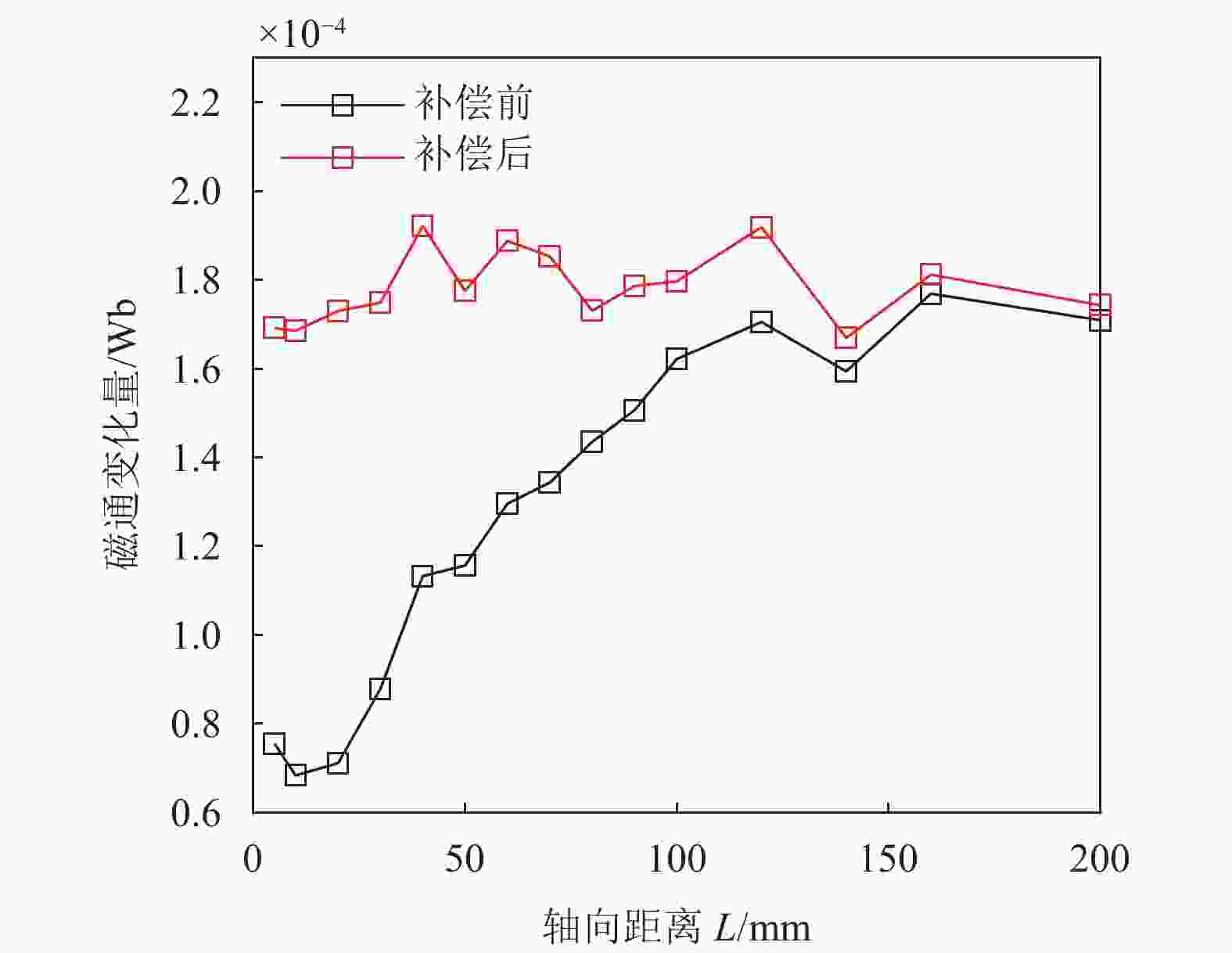
$\Delta B(S{\text{ + }}{S_{{\text{air}}}})$ ,补偿后的磁通量变化量$\Delta {\varPhi _{{\text{ret}}}}$ 为:$$ \Delta {\varPhi _{{\text{ret}}}} = \Delta \varPhi ' + \Delta B(S + {S_{{\text{air}}}}) $$ (8) 对于损伤宽度分别为30 mm和190 mm的钢丝绳模型,根据公式求出损伤宽度补偿后的磁通量变化量。补偿前后的相同损伤率,不同损伤宽度下的磁通变化量如图14所示,能够减弱损伤宽度带来的对定量分析的影响。
-
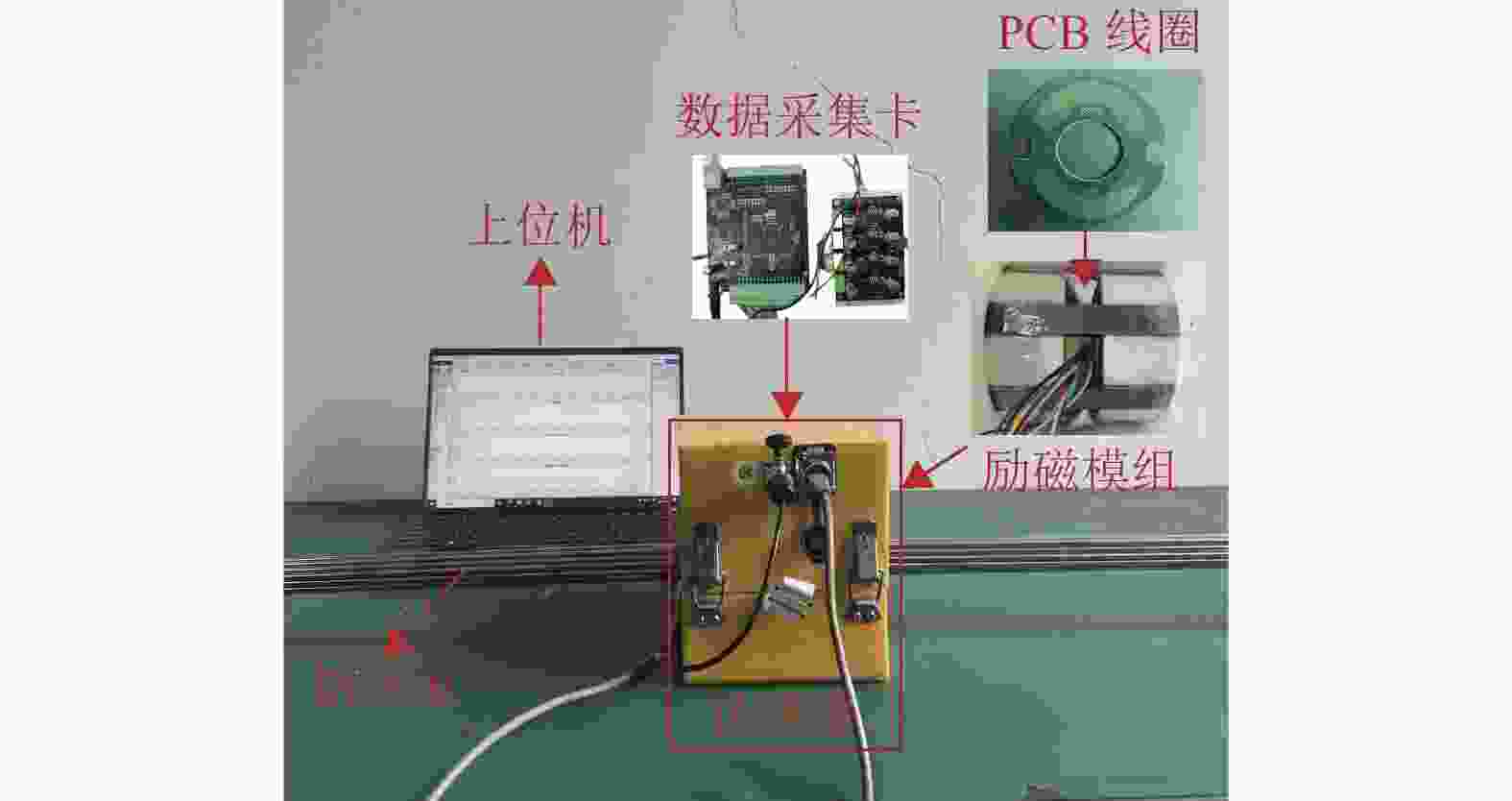
实验过程中为便于设置不同规格损伤进行分析,采用如图15所示的平行钢丝束代替钢丝绳分析。图16为检测钢丝绳的实验平台,利用传感器内部数采卡采集钢丝束的损伤信号,传输至上位机进行进一步处理。实验中为模拟实际钢丝绳直径,采用25根直径5 mm的钢丝与10根直径1 mm的钢丝,构成总横截面积为498.475 mm2的钢丝束。
如图17为实验条件下不同损伤宽度磁通量变化检测量
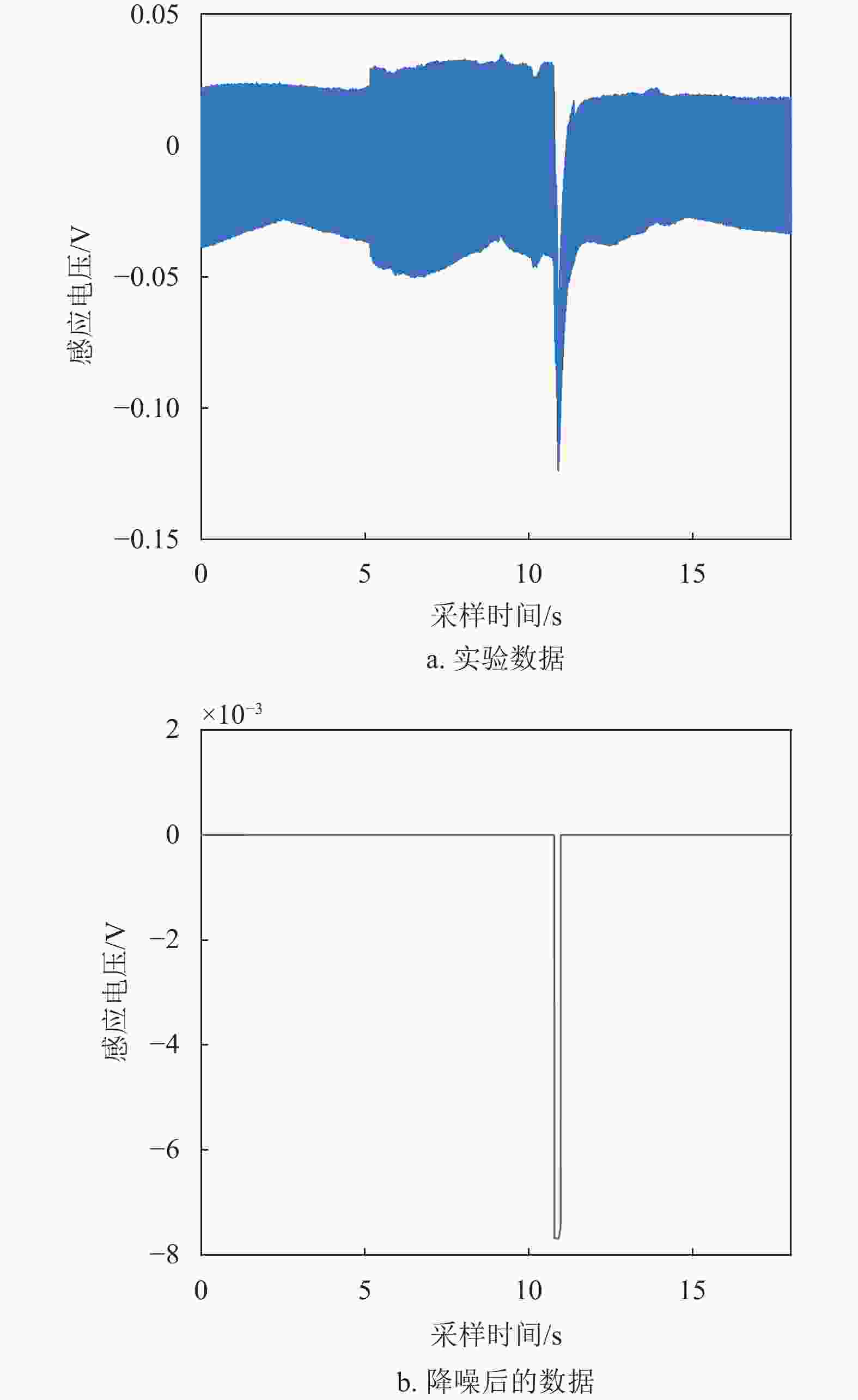
$\Delta \varPhi '$ 及经补偿量$\Delta {\varPhi _{{\text{ret}}}}$ 与损伤宽度之间的关系。由图可得,补偿后的磁通量变化量极大抑制了损伤宽度带来的影响,验证了该补偿方法的有效性。同时,实验设计LMA值为1.56%~86.61%共25组实验作为标准件实验,为了保证实验的稳定性,每组实验进行5次。其中图18(a)为损失率为19.7%时的实验数据之一,通过短时傅里叶变换及小波降噪去除信号中的工频噪声及高频噪声,得到的降噪后的数据如图18(b)所示。图中电压下降信号由于钢丝绳出现损伤导致金属横截面积减少,磁通量变化量增大且为正值,根据式(4),此时电压为负值,当钢丝绳金属横截面积不再继续减少,磁通量变化量为零,因此感应电压也恢复为零值。
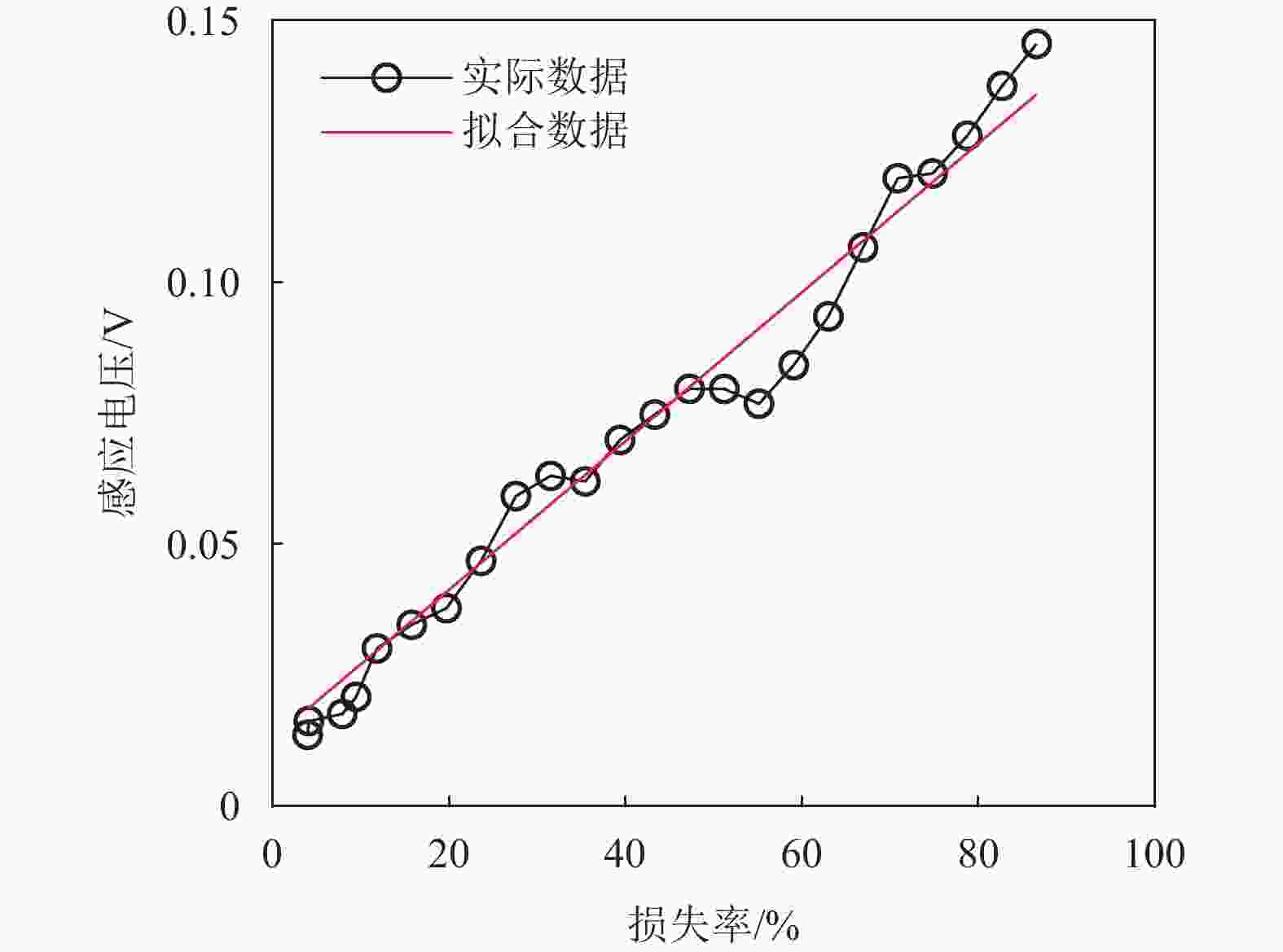
利用上述损伤宽度补偿方法对磁通信号进行补偿处理后,使用线性拟合损失率和电压峰值的函数,拟合结果如图19所示。为验证该函数的有效性,实验采用23根直径5 mm和9根直径为2.5 mm组成的总横截面积为495.78 mm2的钢丝束作为测试组,并设计了1.9%~59.4%共16组不同的LMA值进行验证。通过拟合函数获得16组测试件的LMA估计值,如表2所示,估计值与实际值最大误差为0.8583%,符合国家相关测量标准,具有较好的定量效果。
表 2 不同钢丝束的定量测试结果
实际损失率% 估计损失率% 误差% 1.98 1.331 0.649 2.97 2.3873 0.5827 3.96 3.9366 0.0234 4.95 4.824 0.126 5.94 5.6268 0.3114 6.94 7.0811 0.1411 8.92 8.8452 0.0748 9.9 10.0634 0.1634 15.84 14.2887 0.6951 19.8 19.007 0.793 27.72 27.035 0.165 35.64 34.7817 0.8583 39.6 39.1479 0.4521 47.52 46.9648 0.5552 55.44 54.7817 0.6583 59.4 58.9507 0.4493 -
本文基于主磁通检测原理设计了PCB线圈,利用仿真优化线圈参数、分析损伤宽度对主磁通变化量的影响,提出了改进磁通检测的方法,并通过实验验证了主磁通轴向磁通量补偿法的有效性。最后,通过实验验证了本文所设计的PCB线圈的检测效果和定量误差,得出以下结论:
1) 增加线圈匝数、减小线圈提离值可以显著提升PCB线圈的检测灵敏度,PCB线圈的层数、线宽、线距等参数影响较小,在线圈设计时可依据PCB空间考虑部分参数改善;
2) 损伤宽度会严重影响PCB线圈检测效果,本文提出的损伤宽度补偿方法能够抑制宽度变化带来的影响,同时为线圈定量分析提供稳定数据;
3) 本文设计线圈能够有效检测LMA类损伤,测量误差在1%以内,符合相关检测标准,为实际工况下的钢丝绳定量分析提供新的解决方案。
A LMA Detection Method Based on PCB Coil for Wire Ropes
-
摘要: 钢丝绳金属横截面积损失(Loss of Metallic Area, LMA)直接影响钢丝绳承载强度等特性,因此其检测及定量分析对于设备安全可靠运行具有重要意义。针对目前主磁通检测中存在的线圈绕制困难、参数确定模糊等问题,基于仿真模型提出一种基于印制电路板(Printed Circuit Board, PCB)的分体式线圈结构,分析了设计过程中线圈匝数、线圈层数、线距等参数对检测信号的影响;建立主磁通检测模型,探究损伤宽度对于主磁通检测信号的影响规律,并针对损伤宽度减小造成的信号损失设计补偿方法;最后通过钢丝实验为例验证金属横截面积定量检测效果。实验表明,所提方法定量误差在1%以内,能够有效检测钢丝绳的LMA。Abstract: The loss of metallic area (LMA) directly affects the bearing strength and other characteristics of the steel wire rope, therefore its detection and quantitative analysis are of great significance for the safe and reliable operation of the equipment. Aiming at the problems of difficult coil winding and fuzzy parameter determination in the current main magnetic flux detection, a split coil structure based on printed circuit boards (PCB) is proposed based on the simulation model. The number of coils turns, coil layers, and other parameters in the design process are analyzed for their effect on the detection signal. Meanwhile, the main magnetic flux detection model is established to explore the influence of the defect width on the inductive voltage signal, and a compensation method is proposed for the signal loss caused by the reduction of the damage width. Finally, the steel wire bundle is used as an example to verify the quantitative detection of LMA. Experiment results show that the quantitative error of the proposed method is within 1%, and it can effectively detect the LMA of steel wire rope.
-
Key words:
- Loss of metallic area /
- Main flux detection /
- PCB coil /
- Steel wire rope
-
表 1 PCB线圈设计参数
线圈参数 含义 单位 m 线圈层数 层 z 线圈匝数 匝 d 线距 mm w 线宽 mm e 印刷铜厚 mm h 线圈距钢丝绳表面的提离距离 mm 表 2 不同钢丝束的定量测试结果
实际损失率% 估计损失率% 误差% 1.98 1.331 0.649 2.97 2.3873 0.5827 3.96 3.9366 0.0234 4.95 4.824 0.126 5.94 5.6268 0.3114 6.94 7.0811 0.1411 8.92 8.8452 0.0748 9.9 10.0634 0.1634 15.84 14.2887 0.6951 19.8 19.007 0.793 27.72 27.035 0.165 35.64 34.7817 0.8583 39.6 39.1479 0.4521 47.52 46.9648 0.5552 55.44 54.7817 0.6583 59.4 58.9507 0.4493 -
[1] REN L Y, LIU Z L, ZHOU J G. Shaking noise elimination for detecting local flaw in steel wire ropes based on magnetic flux leakage detection[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-9. [2] ZHANG D L, GAO W, YAN X L. Determination of natural frequencies of pipes using white noise for magnetostrictive longitudinal Guided-Wave nondestructive testing[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 69(6): 2678-2685. [3] ZHOU Z P, LIU Z L. Fault diagnosis of steel wire ropes based on magnetic flux leakage imaging under strong shaking and strand noises[J]. IEEE Transactions on Industrial Electronics, 2020, 68(3): 2543-2553. [4] NI Y C, ZHANG Q W, XIN R Y. Magnetic flux detection and identification of bridge cable metal area loss damage[J]. Measurement, 2021, 167: 108443. doi: 10.1016/j.measurement.2020.108443 [5] 杨叔子. 钢丝绳电磁无损检测[M]. 北京: 机械工业出版社, 2017. YANG S Z. Wire rope electromagnetic non-destructive testing[M]. Beijing: China Machine Press, 2017. [6] ZHOU P, ZHOU G B, ZHU Z C, et al. A review of non-destructive damage detection methods for steel wire ropes[J]. Applied Sciences, 2019, 9(13): 2771-2786. doi: 10.3390/app9132771 [7] 全国试验机标准化技术委员会. 无损检测仪器—钢丝绳电磁检测仪技术条件: GB/T 26832-2011[S]. 北京: 中国标准出版社, 2011. National Testing Machine Standardization Technical Committee. Non-destructive testing instruments—Specifications for the wire rope electromagnetic tester: GB/T 26832-2011[S]. Beijing: China Standard Press, 2011. [8] 全国钢标准化技术委员会. 铁磁性钢丝绳电磁检测方法: GB/T 21837-2008[S]. 北京: 中国标准出版社, 2008. National Steel Standardization Technical Committee. Practice for electromagnetic examination of ferromagnetic steel wire rope: GB/T 21837-2008[S]. Beijing: China Standard Press, 2008. [9] 万强, 沈功田, 刘文贞, 等. 滑索承载索钢丝绳的剩磁检测应用[J]. 无损检测, 2020, 42(8): 20-24. WANG Q, SHENG G T, LIU W Z, et al. Application of residual magnetism testing of load carrying wire rope of strop ropeway[J]. Nondestructive Testing, 2020, 42(8): 20-24. [10] ZHANG D L, ZHANG E C, PAN S M, et al. Fast quantitative method to detect the cross-sectional loss of wire rope defects[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-11. [11] 袁建明. 在役拉索金属截面积测量方法[D]. 武汉: 华中科技大学, 2012. YUAN J M. Measurment methods for metal cross-sectional area of in-service cables[D]. Wuhan: Huazhong University of Science and Technology, 2012. [12] 谭继文, 战卫侠. 基于感应线圈的钢丝绳损伤检测[J]. 青岛建筑工程学院学报, 2001, 22(4): 1-3. TAN J W, ZHAN W X. Test of wire rope damage based on inductance coil[J]. Journal of Qingdao University of Technology, 2001, 22(4): 1-3. [13] YAN X L, ZHANG D L, WANG H P. Increasing detection resolution of wire rope metallic cross-sectional area damage based on magnetic aggregation structure[J]. IEEE Transactions on Instrumentation and Measurement, 2019,DOI: 10.1109/TIM.2019.2947798. [14] YAN X L, ZHANG D L, ZHAO F. Improve the signal to noise ratio and installation convenience of the inductive coil for wire rope nondestructive testing[J]. Ndt & E International, 2017, 92: 221-227. [15] 晏小兰. 钢丝绳金属截面积损伤定量检测关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. YAN X L. Study on key technology of quantitative detection on wire rope metallic cross-sectional area damage[D]. Harbin: Harbin Institute of Technology, 2019. [16] UMA R V, JEBAMALAR T S J, KALADEVI R. A hybrid Mfwt technique for denoising audio signals[C] //International Conference on Innovative Sustainable Computational Technologies: [S. l. ]: CISCT, 2022: 1-6. -


 ISSN
ISSN 



 下载:
下载: